六自由度飞行姿态仿真平台设计

杜航航

（中国民航大学工程技术训练中心，天津 300300）

飞行模拟器是飞机子系统性能验证的载体，其中六自由度运动平台是飞行模拟器的重要组成部分。飞机复杂运动状态模拟过程中，六自由度运动平台可提供滚转、俯仰、偏航以及3 个方向的平移运动[1]。

为便于模拟飞行姿态变化，德国工程师Stewart[2]于1965年设计了六自由度并联机构。与串联机构相比，六自由度并联机构具有结构紧凑、多自由度、高刚性、高精度、误差不叠加等优点[3-4]。六自由度平台运动学分析主要集中于正解与反解问题。其中，并联机构运动学正解是已知关联机构6 个伸缩杆的长度，求解平台的位姿；而反解过程是根据预期位姿逆向求解伸缩杆的长度。王晓飞等[5]利用高精度光栅尺得到驱动杆的长度，进而利用牛顿迭代法进行正解运算。张鑫[6]使用D-H 表示法建立机械结构的空间坐标系，结合齐次坐标变换建立位姿反解方程。李晶[7]基于遗传神经网络进行正解运算，仿真验证该方法具有较高的收敛性。目前常用的正解方法包括解析法与数值法。由于正解方程组具有高度非线性，导致结果不唯一，仅适用于理论分析，实践中多采用反解分析方法进行设计[8]。此外，正解算法计算较复杂，目前仅局限于求解速度与精度。而反解算法较为成熟，使用广泛，但已有研究通常以驱动杆为对象，执行器多采用质量大、价格高的液压、气动、电动伺服等驱动器，导致成品体积大、控制复杂、不易维护[9]。

针对上述不足，设计了以舵机为驱动器的低成本桌面型并联六自由度姿态仿真平台。通过运动学反解，首先求解驱动杆长度，进而通过空间几何解析求得舵机角度变化。该方案将驱动杆的伸缩运动转化为舵机的旋转运动，实现了六自由度平台结构的小型化。

1 运动学反解算法

1.1 空间坐标系建立

并联六自由度平台由上下两个平台及6 条支链组成，每条支链由驱动器、驱动杆及连接铰链构成，Stewart 结构如图1所示。通过6 根驱动杆的协同轴向伸缩实现上移动平台6 个自由度的运动。为便于分析计算，在上移动平台建立活动坐标系，在下基座平台建立静坐标系，将支链与上平台铰链点分别标记为A1～A6，支链与下平台铰链点对应标记为B1～B6。初始位置时，平台处于中位，x 轴及x′轴分别垂直于B4B5及A1A2的连线，z 及z′轴垂直向上，根据右手螺旋法可判定y 及y′轴方向。设上平台A1A2、A3A4、A5A6相邻铰点距离为a,下平台B1B2、B3B4、B5B6距离为b,上平台各铰点外接圆半径为r，下平台各铰点外接圆半径为R，上下平台初始距离为h。为简化公式，记P =

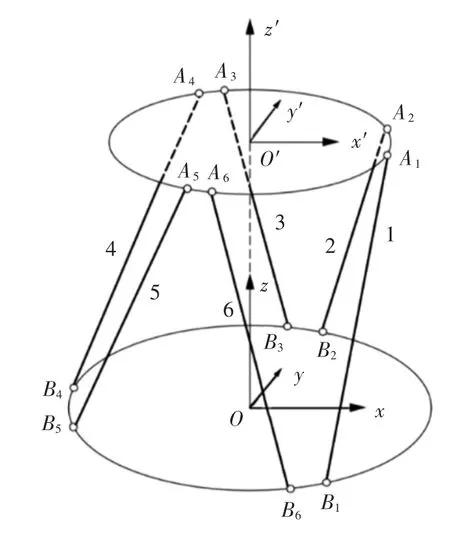
图1 Stewart 六自由度平台示意图Fig.1 Diagram of six-DOF structure

上平台中，A1坐标旋转120°得到A3坐标；下平台中，B1坐标旋转120°得到B3坐标，如此类推，经坐标系旋转变换公式可得上下铰点坐标值，令G 为O 到O′的距离，即

1.2 反解运算

Stewart 型结构上移动平台的位姿变化通过6 根驱动杆的线性伸缩来实现。要求解6 根驱动杆的实时长度，只需将上下平台各铰接点坐标转化到同一坐标系下，再计算两点间距离。动坐标系{O′}（O′x′y′z′)相对于参考坐标系{O}位置和姿态可通过有限次数的平移变换与旋转变换得到。

将坐标系{O′}在x、y、z 轴方向上分别平移dx、dy、dz 距离，3 次平移变换矩阵分别为T1、T2、T3，然后依次进行3 次旋转变换，绕z 轴、y 轴、x 轴分别旋转α、β、γ角度，3 次旋转变换矩阵分别记为T4、T5、T6。可得动坐标系到参考坐标系的齐次坐标变换矩阵T，为

其中：sα=sin α，cα=cos α，sβ、cβ、sγ、cγ 同理。已知某坐标系中任意一点的坐标值，可通过左乘齐次坐标变换矩阵T，将该点位置向量变换到另外一个坐标系中。将上移动平台各铰点变换后齐次坐标记为Pi=（Pix，Piy，Piz，1），通过齐次坐标变换，可得到静坐标系下的坐标Ai=（Aix，Aiy，Aiz，1），i=1～6。则有

在下基座平台中，设各铰点坐标为Bi=（Bix，Biy，Biz），在同一参考坐标系下，驱动杆实时长度（即上下铰点间的距离）可由AiBi的长度计算求得，即

由以上过程可解算六根驱动杆的实时长度，由此完成了运动学反解过程。

1.3 舵机角度计算

舵机连臂通过万向球头连杆连接上下铰点，反解过程已得到Li，选用舵机为执行机构，通过控制转动角度实现上下平台对应铰点间距离的变化，求解驱动杆伸缩量变化就转化为求解舵机角度θ。根据反解运算过程，可获取上平台6 个铰点在参考坐标系中的坐标，进而通过几何解析法求出各舵机转动角度。由于万向球头的存在，连杆与舵机连臂所在平面与舵机轴转动方向不重合，简化的空间结构如图2所示。

在空间内将F 点投射到下平台,如图3所示，可计算F 点坐标值，设上平台铰点P 动态坐标为（Px，Py，Pz），根据向量OB+BF+FP+PO′+O′O=0 运算将各点坐标代入，利用|PB|=L，则有

|cos φ·OF+sin φ·cos θ·BF-Px′-sin φ·OF+

图2 舵机连杆结构示意图Fig.2 Diagram of servo connecting rod

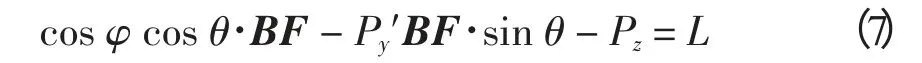
将上述公式展开，令

其中：V 为可以实时计算的已知量，则可得到

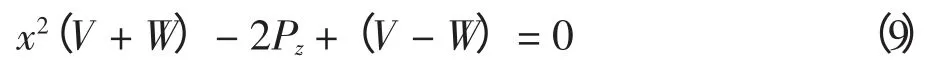
求解该一元二次方程并求解角度θ，可得

图3 F 点在参考坐标系中的投影Fig.3 Projection of point F in reference coordinate system

2 Solidworks 仿真设计

在Solidworks 中建立六自由度姿态仿真平台模型，如图4所示。执行机构全部按实际参数设计，通过软件装配体功能，将各零件模型通过相关约束关系进行装配。软件可控制某一舵机的转动角度，分析6 条驱动杆运动间的耦合，以及位姿调节实现范围，设计参数及6 个自由度可调节范围分别如表1和表2所示。

图4 六自由度平台仿真模型Fig.4 Simulation model of six-DOF

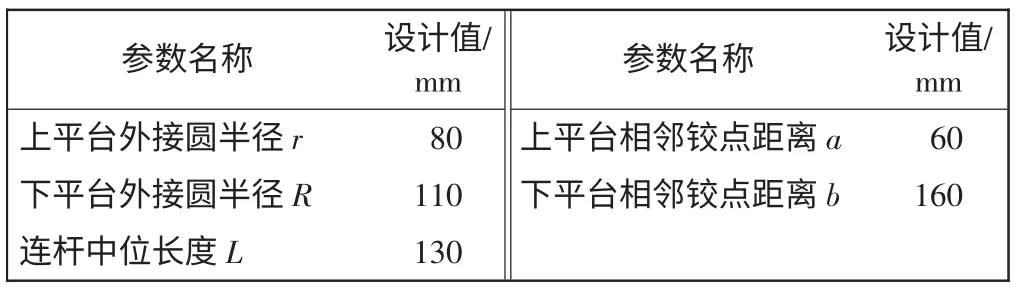
表1 六自由度平台主要运动参数Tab.1 Main motion parameter of six-DOF

表2 平台位姿变化范围Tab.2 Motion range of six-DOF

3 运动平台控制系统设计

运动平台控制系统是上位机解算单元与平台执行机构的连接部分，控制系统如图5所示。上位机通过运动学反解将所对应的位姿数据转化为舵机角度值发送给控制系统，控制系统根据接收到的6 个舵机角度值控制相应舵机转动。

图5 控制系统框图Fig.5 Block diagram of control system

控制板核心处理器为STM32F103 单片机，最大速度为72 MHz，主要用于接收指令控制舵机转动，运动学反解及舵机角度解算任务全部在PC 端完成。这种处理方式解放了下位机的运算解析过程，上位机以10 Hz的高频率向控制板发送角度指令，舵机转动实时性好，平台运动过程无卡顿情况。

4 平台测试

4.1 输入输出响应测试

由上位机软件在x 轴方向上输入x=10cos（0.1πt）位姿曲线，如图6所示。6 个舵机角度呈周期性平滑变化，如图7所示。舵机角度变化频率与平台输入一致，与其它自由度单独测试结果一致，验证了平台结构及参数设置的合理性。实测表明，该平台可满足多自由度同时输入运行，各自由度角度误差在±1.5°范围内，平移误差在±5 mm 范围内。

图6 x 轴余弦输入曲线Fig.6 Input cosine curve of X-axis

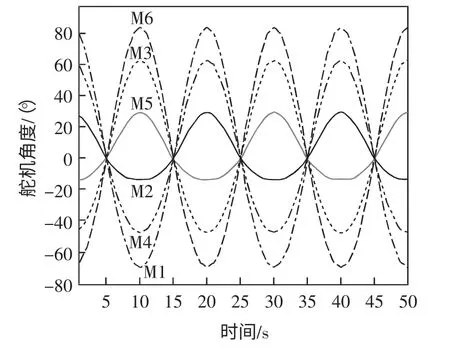
图7 x 轴余弦输入舵机角度变化曲线Fig.7 Curve of servo gear angle with cosine input of X axis

4.2 P3D 联机测试

飞行模拟器软件P3D（Prepar 3D）姿态数据通过共享内存的方法进行提取，当两个进程通过页表将虚拟地址映射到物理地址时，在物理地址中有一块共同的内存区，即共享内存，可被两个进程同时读取使用。模拟器软件Prepar 3D 及所设计的MFC 接口程序通过共享内存的办法进行数据共享，使进程间无需传送数据，而是直接通过内存访问，提高了程序的效率。获取实时飞行姿态数据后，通过运动学反解先求出驱动杆的伸缩量，进而求解舵机角度，然后向单片机发送舵机角度控制参数。测试结果表明，通过共享内存方法，飞行姿态数据抓取实时性好、效率高，下发数据实时性好，姿态仿真平台在获取下发指令后能进行快速响应，并可与P3D 模拟飞行软件联动，进行虚实结合的飞行姿态仿真。

图8 模拟飞行软件与仿真平台联机测试Fig.8 Joint test of flight simulation software and simulation platform

5 结语

结合实际应用需求，设计了以舵机为执行机构的桌面型六自由度姿态仿真平台，根据运动学反解理论进行驱动杆伸缩量的解算，进而求解出舵机转动角度。该仿真平台体积小、成本低、易于维护，既可以单独通过上位机软件运行，也可与P3D 模拟飞行软件联动，性能稳定。该平台实现了对滚转、俯仰、偏航及3 个方向平移运动的仿真控制。后续研究将考虑速度及加速度控制，以实现更逼真的模拟器姿态仿真效果。