带圆角的平板接触模型与有限元分析
2020-10-31张汉玉徐文君
张汉玉,徐文君
(中国民航大学工程技术训练中心,天津 300300)
叶片是航空发动机的重要构件,在工作环境恶劣情况下,尤其是涡轮叶片,要承受高温高压燃气的高速冲击。据统计,发动机结构性故障中,叶片是研制和使用过程中故障率最高的零件之一,占发动机总故障的30%以上[1-2]。因而,最大限度地降低叶片结构在工作中的振动应力是十分必要的。工程上通常利用干摩擦阻尼器来消耗叶片的振动能量,以实现减振的目的。
在干摩擦阻尼器设计或计算中,接触刚度通常是最先要确定的参数,然而,接触刚度一般较难确定,往往依赖经验给定一个较为合理的数值[3]。郝燕平等[4]提出带阻尼器的叶片振动响应实验和理论计算相结合的方法,并研究了接触面法向正压力及激振力对接触刚度kt的影响规律,得出kt·为的三次函数。按照该结论,当激振力不变时,随着法向正压力的增加,接触刚度kt也随之增加,且趋向于无穷,这与实际不符。史亚杰等[5]通过有限单元法对干摩擦阻尼的接触刚度进行求解,并分析了接触面法向正压力、摩擦系数、接触面大小等对接触刚度的影响规律。何尚文等[6]引入弹性剪切层,给出了正压力恒定时的接触刚度计算方法。漆文凯等[7]采用整体-局部滑动模型,结合有限元软件对等效刚度进行了分析。以上研究,在计算接触刚度时,使用的是直角平板接触模型,且将法向正压力简化为恒力或二次函数形式,显然没有考虑到接触边缘的应力集中问题,与实际分布情况差别较大,导致接触刚度的计算结果不可靠。
虽然前人已对阻尼器接触刚度进行一定研究,但尚无一种准确有效的计算方法。因此,提出将理论推导与有限元计算相结合的方法,并使用带圆角的平板接触模型来计算接触面上的法向正压力、切向力以及接触刚度;使用有限元软件对接触模型进行模拟计算,并拟合出接触刚度随正压力变化的关系式,从而,可以获得较为简便可靠的接触刚度计算方法。
1 接触刚度理论推导
1.1 接触模型
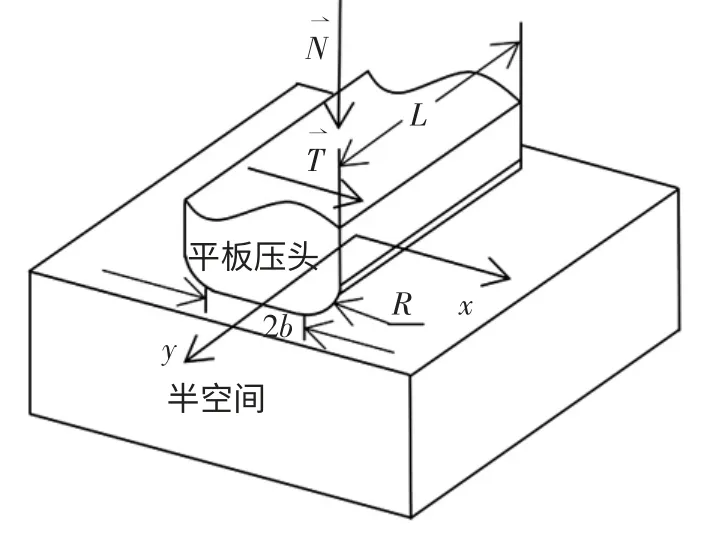
图1 带圆角的平板接触模型Fig.1 Flat contact model with rounded edges
为了得到切向刚度的表达式,假设:①接触面上的受力沿着y 向均匀分布;②接触面上的压力和剪力沿x 向的分布可由二维接触分析得到,即忽略了有限长平板的边缘效应。
1.2 二维模型中正压力和切向力分布
沿y 向提取一个单位长度的平板进行分析,如图2所示。其中,和对应单位长度的法向正压力和切向力;a 为未添加正压力时x 向的接触长度;c 为添加切向力后x 向的粘滞长度。

图2 二维接触模型Fig.2 2D contact model
接触面的法向正压力分布[8]为

式中,sin φ0=a/b。
利用压力分布公式(1)可得到正压力p(x)随接触长度x 的变化曲线,并将纵坐标的p(x)和横坐标x 分别以(P/b)和b 进行无量纲处理,即:横坐标的取值范围从[-b,b]变为[-1,1],从而纵坐标的取值范围也随之改变,如图3所示。
前列腺炎是成年男性常见的泌尿系统疾病,主要分为急性和慢性起病,临床上将其分为4型[1]。在中医,前列腺炎可属于“淋证”、“精浊”、“腰痛”等范畴。慢性前列腺炎(chronicprostatitis,CP)并不危及生命,但严重影响患者的心理与生理健康,降低患者的生活质量与幸福指数[2]。目前,主要的治疗方法疗效并不理想,针刺作为一种传统的中医药疗法,近年来已有许多临床研究证实其有效的治疗作用,为了对针刺与其他治疗方法进行更客观的疗效对比开展了本项Meta分析。
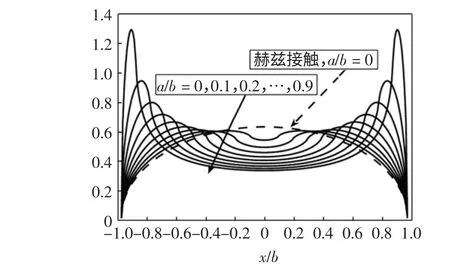
图3 法向正压力p(x)沿x 向的分布Fig.3 Normal pressure distribution along x axis
图3中描述了a/b 取不同值时,法向正压力的分布曲线。当a/b=0 时,即未加载法向正压力,初始接触长度a=0,此时的接触模型可以转化为“圆柱-平板”接触;随a/b 逐渐增加,接触面两端的正压力最大值max[p(x)]逐渐变大,而中心位置的正压力最小值min[p(x)]逐渐变小;当a/b=1 时,即接触面的初始长度与加载后的长度一致,此时接触模型可转化为“平板-平板”接触。
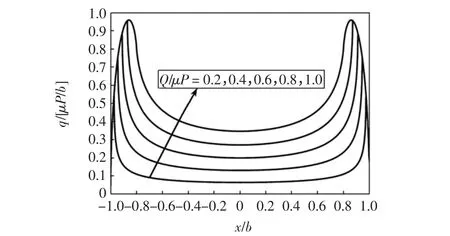
图4 切向力q(x)沿x 向的分布Fig.4 Tangent pressure distribution along x axis
1.3 切向力与切向位移
前文分析了2D 接触模型的压力分布,这种方法并不能直接确定切向力和切向相对位移之间的联系。当已知3D 接触模型的法向正压力与切向力时,Johnson[9]提出了一种方法来确定切向力和切向相对位移之间的关系,从而来计算迟滞环。
将切向力q(x)施加在弹性半空间上,如图5所示,则位移为
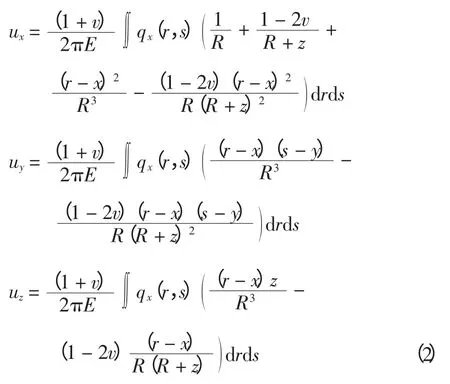
其中:E 为弹性模量,v 为泊松比;R2=(x - r)2+(y -s)2+z2。

图5 半空间局部受载示意图Fig.5 Local load of half-space
在目前的研究中,接触面的相对位移被认为是一维的,沿x 方向。令x=y=z=0,得到接触中心的位移为

由于接触面上的法向正压力与切向力是关于接触中心对称分布的,可得到
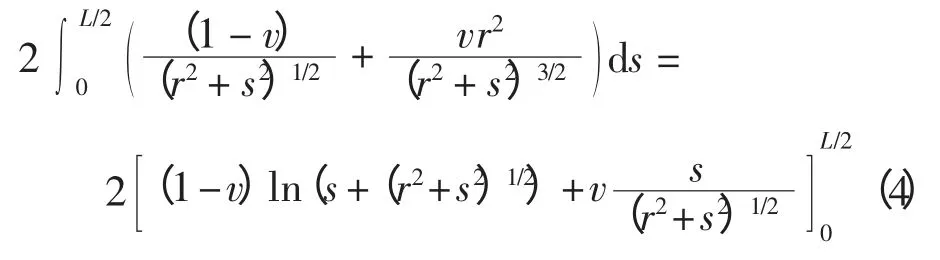
考虑到L≫b 和-b ≤r ≤b,有L≫r。式(4)可近似地写为
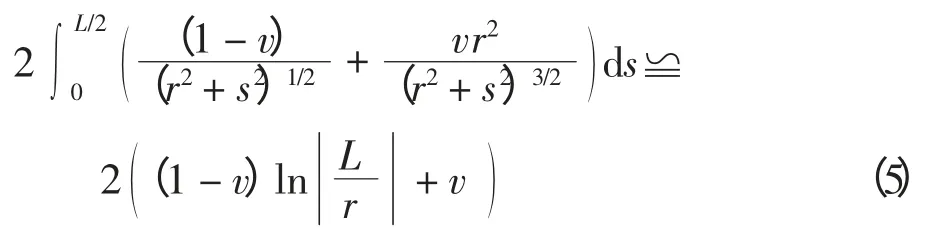

因此,接触面上边缘区域接触点的切向相对位移可表示为

式中,E*=2(1-v2)/E。
根据刚度的定义,可将接触刚度表示为

进而可得到接触刚度kd,再由Mindlin 球接触理论可得到法向接触刚度为

2 切向接触刚度的有限元计算
2.1 有限元模型
首先,建立带圆角的“平板-平板”接触模型,如图6所示。模型由阻尼块和地面组成,分别采用四边形平面应变单元进行分网。考虑到结果可靠性要求,对接触区域进行了模型网格的收敛性分析,确定最佳的细化网格。材料属性为:弹性模量为E=1.07×105MPa,泊松比v = 0.3。边界条件和加载情况为:对地面所有节点的位移全约束;对阻尼块施加法向力及切向力。这样便可以得到接触面在正压力和切向力作用下的切向位移,如图7所示。

图6 有限元模型Fig.6 Finite element model

图7 接触面切向位移云图Fig.7 Tangent displacement nephegram of contact surface
接触刚度kd为阻尼块左侧的切向力和引起的接触点的滑动距离的比值,即

2.2 接触刚度确定
根据1.3 节提出的方法,分别求解不同摩擦系数及不同受力情况下的接触刚度。在阻尼块上表面施加20 N 法向正压力,选取摩擦系数为μ=0.3 时,切向位移计算结果如表1所示。由表1中的数据计算得出切向力与接触点切向位移的关系,如图8所示。

表1 正压力为20 N 时的切向位移计算结果Tab.1 Calculation result of tangential deformation when normal pressure is 20 N

图8 μ=0.3 时切向力与切向位移的关系Fig.8 Tangential force vs.deformation at μ=0.3
从图9可看出,保持正压力不变,切向力较小时,接触点的切向位移与切向力成线性关系,当切向力变大直至接近最大静摩擦力时,切向力和变形不再满足线性关系。因此,当正压力一定时,可通过求解图8中直线段的斜率来获得不同摩擦系数对应的切向接触刚度。计算了选取不同正压力时,3 种摩擦系数对应的切向接触刚度,如表2所示,并以此绘制了接触刚度和正压力的关系曲线,如图9所示。
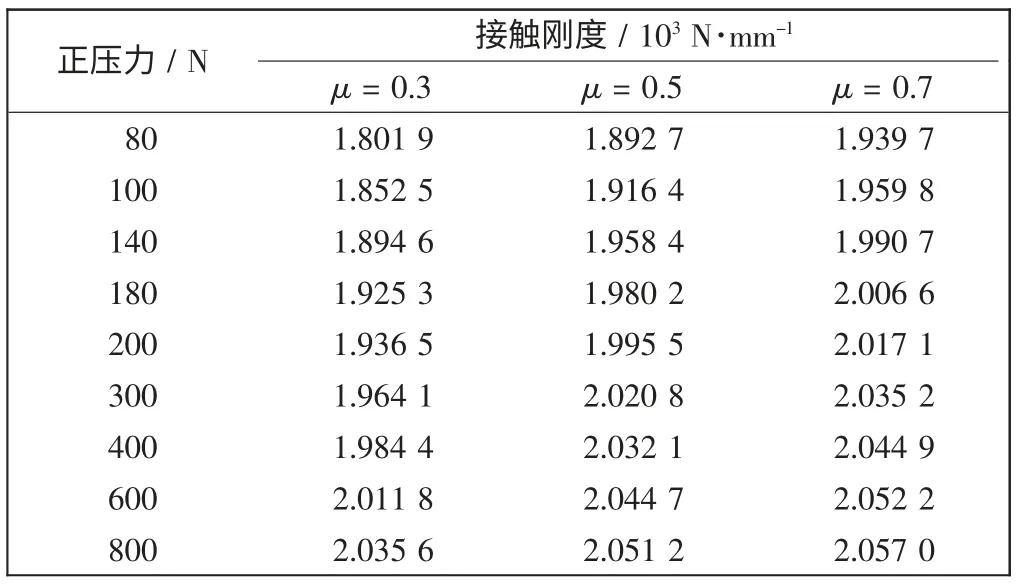
表2 不同摩擦系数下正压力对应的接触刚度Tab.2 Contact stiffness vs normal pressures with different friction coefficients

图9 不同摩擦系数下接触刚度和正压力的关系曲线Fig.9 Contact stiffness vs.pressure with different friction coefficients
由图9可看出:当选取不同正压力时,接触刚度值变化很大,接触刚度随正压力的增加而逐渐增加;当正压力足够大时,接触刚度增加的速度趋于平缓。
在叶片的实际振动过程中,接触面上的受力会在一个振动周期内发生很大变化,特别是叶冠和凸肩,这会导致接触刚度也发生相应的变化。为了在叶片非线性响应计算中获得准确的接触刚度及摩擦力,需要考虑这种变化。以摩擦系数μ=0.3 的计算结果为例,选择幂函数形式进行曲线拟合,如图10所示。
当弹性模量E=1.07E5 MPa,泊松比v=0.3 时,通过拟合图10中接触刚度与正压力的关系曲线,得到接触刚度和法向正压力之间的关系式为对原数据点的拟合精度颇高,R2为99.49%。可认为,在该正压力范围内,摩擦块与地面之间的接触刚度随正压力变化呈现幂函数形式的变化规律。

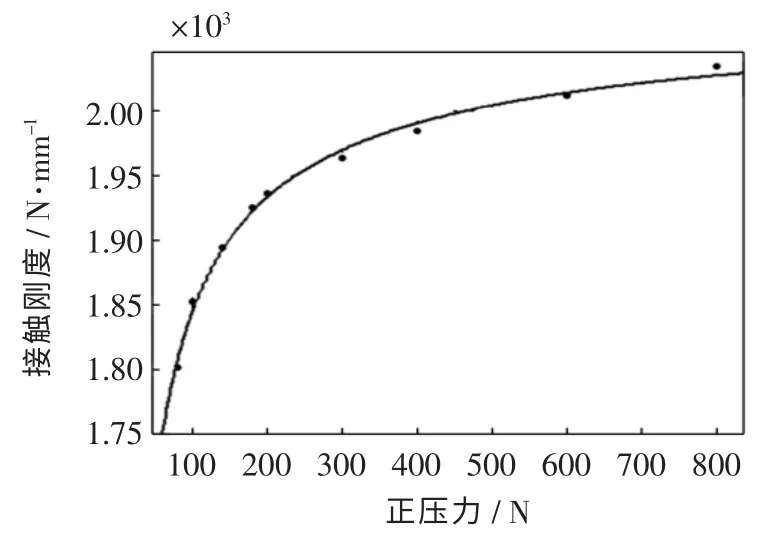
图10 μ=0.3 时接触刚度变化曲线Fig.10 Change curve of contact stiffness at μ=0.3
用同样的拟合形式,分别对摩擦系数为μ=0.5 和μ=0.7 两种情况进行拟合,如图11和图12所示。
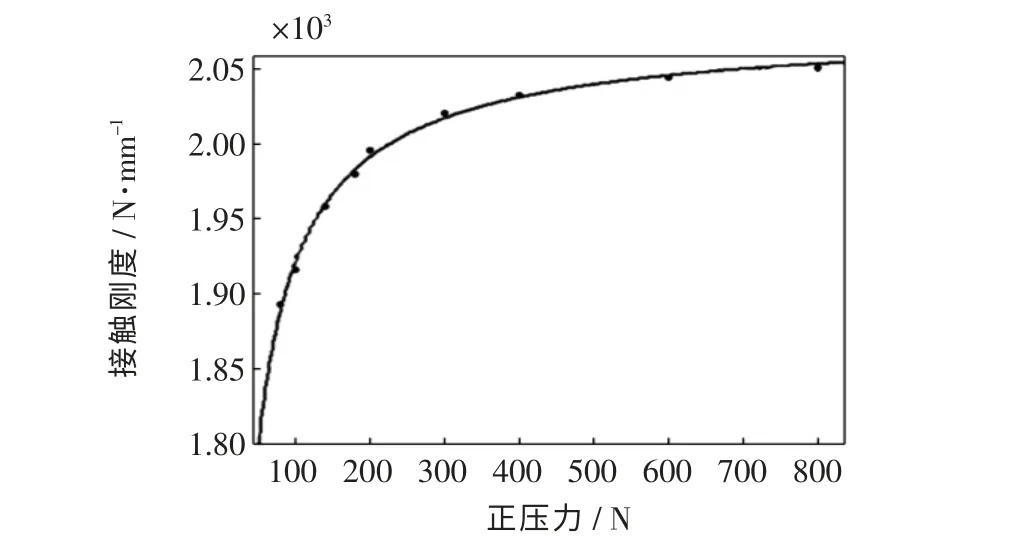
图11 μ=0.5 时接触刚度变化曲线Fig.11 Change curve of contact stiffness at μ=0.5

图12 μ=0.7 时切向接触刚度变化曲线Fig.12 Change curve of contact stiffness at μ=0.7
当μ=0.5 时,切向接触刚度和法向正压力之间的关系式为

对原数据点的拟合精度颇高,R2为99.65%。
当μ=0.7 时,切向接触刚度和法向正压力之间的关系式为对原数据点的拟合精度更高,R2为99.76%。

得到接触面上接触刚度kd随正压力的变化规律后,则相应的法向接触刚度则可以利用式(9)进行计算,当泊松比v=0.3 时,kn≈1.21kd。
3 结语
首先分析了带圆角的平板接触模型接触面上的受力情况,讨论了平板圆角的变化对接触面上正压力和切向力分布的影响;根据刚度定义,并结合接触点的位移分布,给出了接触刚度和法向正压力之间的关系。
然后,利用数值仿真对接触刚度的求解方法进行了模拟计算,得到可用来描述正压力与接触刚度关系的表达式,并得到以下结论:①接触刚度会因接触面上正压力与摩擦系数的不同而变化;②接触刚度随接触面上正压力的增加而变大,并呈幂函数关系;③接触刚度随摩擦系数增加而增大,正压力越大,接触刚度随摩擦系数的不同而变化越显著。
上述方法可快捷准确地得到正压力与接触刚度的关系表达式。接触刚度的准确性直接决定了接触面的接触状态变化,实时地考虑接触刚度能够更加准确地分析接触点从粘滞到滑动的变化过程,为迟滞环以及叶片响应的正确计算提供了保证。
