基于多源异构数据的航班追踪盲区评估

韩 萍，张秉清，张 喆，卢晓光

（中国民航大学电子信息与自动化学院，天津 300300）

航班追踪是指航空承运人在航空器的整个运行区域对其进行追踪。马航MH370 失联事件后，国际民用航空组织（ICAO）于2014年5月在蒙特利尔举行了全球航班飞行追踪多学科特别会议，提出了全球航班追踪近期、中期和远期的工作建议。2015年11月ICAO 理事会通过了《国际民航公约》附件6 第Ⅰ部分的第39 次修订，要求航空承运人实现在航空器的整个运行区域对其进行追踪，并制定了例行航空器追踪规范，其中，“4D”指航空器的位置信息（经度、纬度、高度、时间）[1]。在实际航班追踪过程中，会发生航空器位置报告缺失的情况，即地面没有在所规定的时间间隔内收到来自航空器的自动位置报告。文中主要对追踪盲区原因而造成的位置报告缺失进行研究。航班追踪盲区是指地面站有效信号不能完整覆盖的区域，会导致航空器追踪使用的卫星、甚高频、高频等通信链路在某些区域容易出现通信信号不稳定，航空器追踪自动位置报告中断的情况[2]。ACARS 和ADS-B 是目前最常用的航班追踪手段[3-4]。

文献[5-6]通过电波传输损耗模型和甚高频基站参数计算甚高频信号覆盖范围和覆盖盲区；文献[7]基于视距传播原理及电磁波传输距离结合区域高程计算甚高频信号的覆盖范围。以上均无法从数据端分析出盲区的分布。国内外对雷达或甚高频信号覆盖盲区问题研究主要集中在甚高频基站及其电磁波传输损耗等方面，需要高程数据、甚高频站台功率、位置等大量先验信息。因此，基于实际ACARS 和ADS-B 追踪数据源，通过数据挖掘方法，针对航班追踪盲区评估问题展开研究，建立了航班追踪盲区评估模型，为航空公司、局方开展的航班追踪性能评估工作提供借鉴。

1 模型原理

由于模型需要研究盲区位置概率分布，需要将数据进行预处理，估计出位置报告缺失点的位置，可选取合适的插值方法对其进行插值，得到缺失点位置之后，应用数据挖掘方法得到盲区的分布。根据区域中航迹点分布特点，将该问题转化为区域内部的分类问题，得到区域内每个位置成为盲区的概率。

1.1 三次样条插值原理

三次样条插值算法作为最常用的插值方法，其一阶导数和二阶导数都是连续的，利用导数连续性，可将分段生成的曲线拟合成完整、较为平滑的三次样条曲线[8]。考虑到飞机飞行曲线的连续性和光滑性，选择三次样条曲线作为航迹插值曲线，由于三次样条曲线连续且二阶可导，因此，可最大程度地对航迹进行拟合[9]。

三次样条曲线的基本形式为，给出一组数据点，通过对每个样本点的分段三次多项式曲线拟合输入点，得到三次样条曲线。对追踪报告数据中缺失点的位置信息进行重构，包括经度和纬度。

假设数据中有n+1 个样本点，样本点坐标为

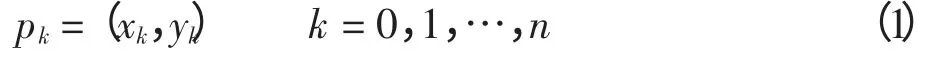
三次样条算法插值拟合的示意图如图1所示，n+1 个样本点组成了n 个区间，其中，每个区间都是一个三次多项式，样条由连续的4 个点得到，pk和pk+1为曲线的端点，pk-1和pk+2则用于计算曲线端点处的斜率。由于曲线是光滑的，因此，三次曲线的一阶导数和二阶导数在一个区间内都是连续的。

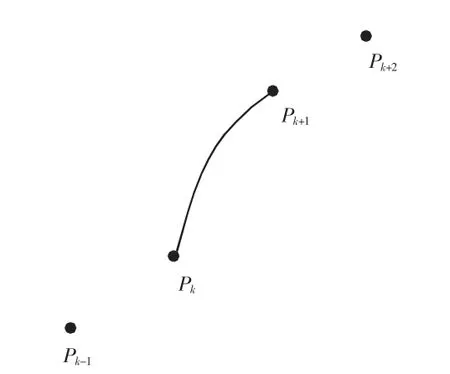
图1 三次样条插值示意图Fig.1 Illustration of cubic spline interpolation

假设在点pk和pk+1之间的区域存在缺失点，可利用含有参数的三次方程组来拟合缺失区域的该段曲线，即

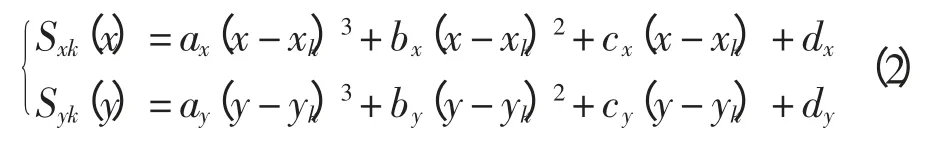
其中：Sxk、Syk分别代表在X 轴和Y 轴两个维度上[pk，pk+1]区间上的三次样条曲线。若得到该三次样条曲线，需要得知a、b、c、d 4 个参数的取值。由端点边界条件可知

其中：ik表示xk或yk。由于节点达到二阶连续，因此，其一阶、二阶微分具有以下性质

在经纬度坐标系下，由于纬度不同，相同的经度变化引起的球面距离变化并不相同。因此，为使三次样条插值法得到的缺失点位置更加精确，将坐标统一为平面笛卡尔坐标系。使用墨卡托投影法，将经纬度（lat，lon）转换为平面坐标（X，Y），则

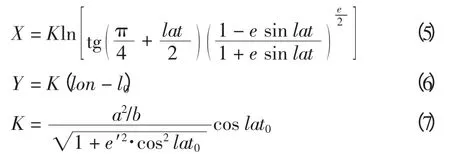
1.2 基于高斯核函数的SVM 分类原理

SVM 分类算法适合小样本学习，其思想是利用样本空间中的超平面将样本进行区分。对于非线性分类问题，SVM 需要借助核函数来解决，SVM 中有多种核函数，如线性核函数、多项式核函数、高斯核函数、Sigmoid 核函数等[11-12]。

SVM 算法的决策判别函数为

其中：ω 为权向量；b 为偏置向量。

SVM 优化模型为

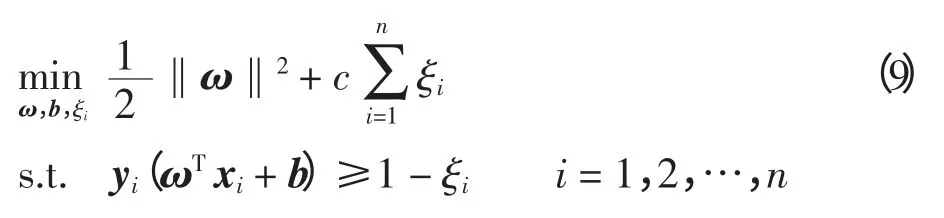
其中：ξi为松弛变量，反映样本被错分的程度；c 为惩罚因子，代表模型对错分样本的容忍度。在式（9）二次规划问题求解过程中，数据样本的内积即为核函数。

在无法得知航迹点的先验信息时，高斯核函数更具优势：与线性核函数相比，可将样本映射到一个更高维的空间，可很好地处理当类标签和特征之间的关系是非线性时的样例，有效地解决了非线性二分类问题；与多项式核函数相比，多项式核具有更多的超参数，相比之下高斯核函数更加简便；与Sigmoid 核相比，Sigmoid 核计算得到的核矩阵不一定是正定矩阵，且基于Sigmoid 核构造的SVM 模型在准确性上通常也不如高斯核函数[13]。因此，选择高斯核函数作为非线性分类所用的核函数。高斯核函数也称径向基（RBF）函数，是空间两个向量欧氏距离的单调函数，其表达式如下

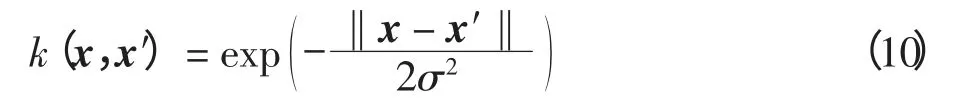
式中，涉及到两个点的欧氏距离（2 范数）计算：x′为核函数中心，代表缺失点的位置；σ 是带宽，控制核函数的作用范围，σ 越大，x′影响的范围越大；x 代表缺失区域内任意一点，随着x 和x′的距离增大，其影响值k（x，x′）将逐渐减小，直至无限远处变为0[14]。

2 追踪盲区评估模型

假设模型满足以下条件：①评估区域内所有位置报告缺失问题都是由追踪盲区因素引起的；②航班追踪信息等时间间隔发送；③信号覆盖盲区固定不变，不会因自然或人为原因改变盲区状态。

模型的整体框架如图2所示。首先对评估区域进行预处理，将评估区域进行网格化处理，且根据数据点的分布情况划分出缺失点集中的缺失区域；利用基于高斯核函数的SVM 二分类原理得到缺失区域内的盲区位置概率分布；最后代入测试数据验证模型性能。

2.1 评估区域预处理

先对评估区域进行网格化处理，将连续的评估区域平均划分成大小相同的网格。由于模型采用平面笛卡尔坐标系，X 轴和Y 轴均以1 km 为划分单位将空间划分为n 个1 km×1 km 的正方形网格。

针对发生位置报告缺失的航班，选取一块矩形评估区域，从中划分其航迹点覆盖区域和缺失区域，划分的示意图如图3所示。其中，航迹点覆盖区域为评估区域内所有航班在整个评估区域内可能经过的区域，包括区域边界与平面坐标系X 轴的夹角和航迹点覆盖区域的宽度；缺失区域为航迹点覆盖区域内部仅包含缺失点的区域，为发生位置报告缺失最严重的区域。因此，模型只对缺失区域内部的盲区位置概率分布进行研究。

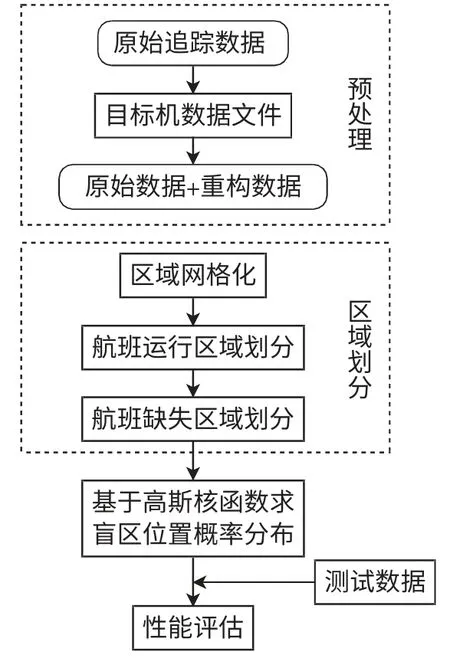
图2 模型整体框架Fig.2 Model framework

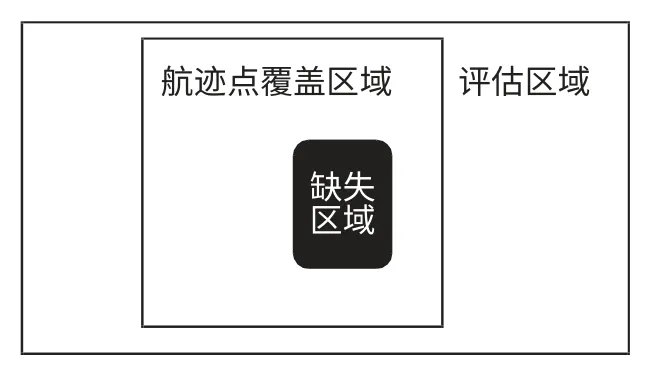
图3 评估区域预处理示意图Fig.3 Evaluation area preprocessing diagram

假设区域内的航迹点{p1，t，p2，t，…，pn，t}与下一时刻的航迹点{p1，t+1，p2，t+1，…，pn，t+1}，得到每个对应点航向角{θ1，θ2，…，θn}。如果下一时刻的点为缺失点，则用重构的航迹点代替，得到航迹点覆盖区域边界与横坐标夹角利用得到的θ 作平行线，找到能够覆盖区域内所有航迹点的最大宽度作为航迹点覆盖区域的宽度。随后在航迹点覆盖区域根据重构缺失点的位置划分出缺失区域，如图4所示。

图4中外围线为航迹点覆盖区域的边界，形状为平行四边形，黑色点为正常航迹点，白色点为重构缺失点。以航班运行方向作平面坐标轴，Y 轴平行于航迹点覆盖区域的边界，X 轴垂直于航迹点覆盖区域的边界；根据Y 轴找到最大包含全部重构缺失点的区域[y1，y2]，再在区域中根据X 轴确定X 轴范围[x1，x2]，保证缺失区域内不包含正常点；最终确定缺失区域ABCD；最后将区域内所有航班的缺失区域求并集得到总的缺失区域。

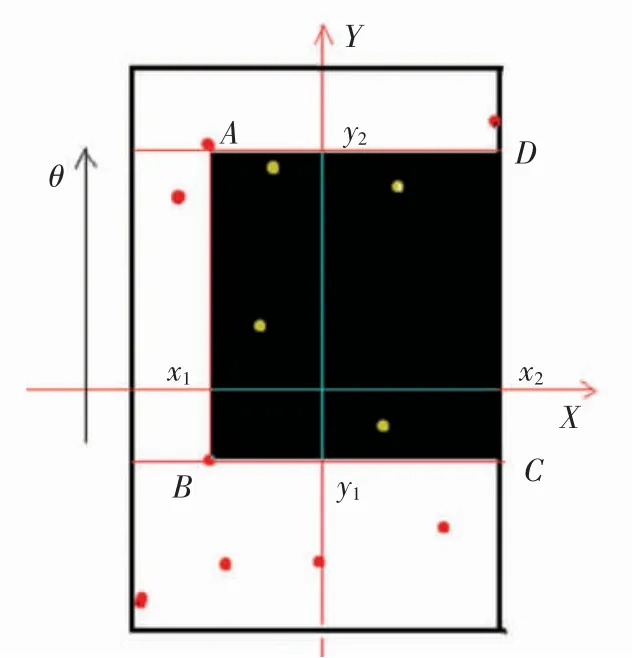
图4 划分缺失区域示意图Fig.4 Missing area division diagram

按上述方法得到这些航班的航迹点覆盖区域{A1，A2，…，An}，再根据重构缺失点的位置得到矩形缺失区域{B1，B2，…，Bn}，最终得到总的航迹点覆盖区域和缺失区域如下

2.2 盲区位置概率分布

设空间中有n 个缺失点{l1，l2，…，ln}，每个缺失点根据到其最近邻正常点距离的不同，分配不同的权值，距离最近邻正常点越近，证明该缺失点越靠近缺失区域边界，分配到的权值就越小，反之则越大。设其权值分别为{w1，w2，…，wn}，区域内每个缺失点到其最近邻正常点距离为{d1，d2，…，dn}，则每个缺失点分配到的权值为

设空间中的一个网格g 对应的中心点x，得到这个点在空间中受到空间中缺失点的影响值总和为

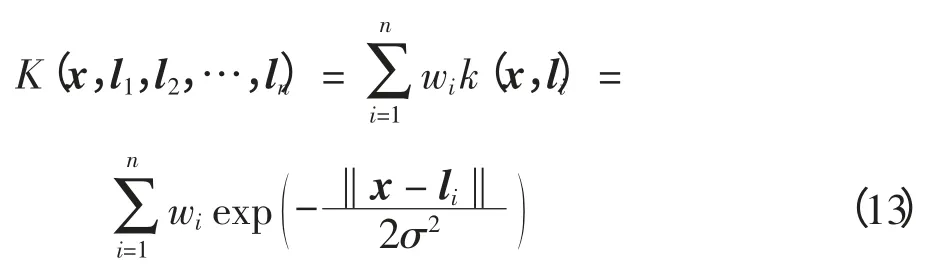
影响值即以缺失点为中心的高斯函数在中心点x上得到的值。最终得到的影响值作为网格为盲区的概率值，值域为[0，1]。

3 实验与分析

选用某航空公司一个月内多个航班ACARS 追踪数据进行实验，从中选出位置报告缺失多发区域作为评估区域，如图5所示。

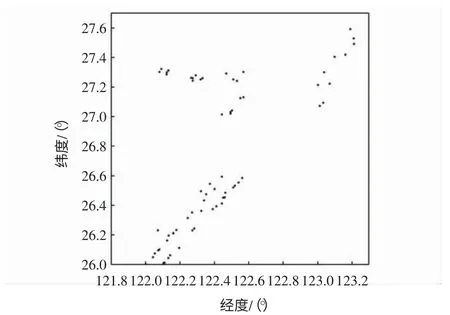
图5 位置报告缺失多发区域航迹点分布示意图Fig.5 Track point distribution in missing areas

3.1 追踪数据预处理

对于追踪数据的预处理主要是对缺失的追踪数据进行插值。假定在航班追踪过程中飞机巡航高度保持不变，仅在二维平面区间内对航迹进行插值，通过墨卡托投影可有效地将经纬度坐标转换为平面坐标，再利用转换后的坐标系对存在位置报告缺失的航迹进行插值及盲区生成，待算法完成后再将平面坐标转换回经纬度坐标，以得到准确的航迹信息。

应用三次样条插值算法得到的缺失点位置如图6所示。

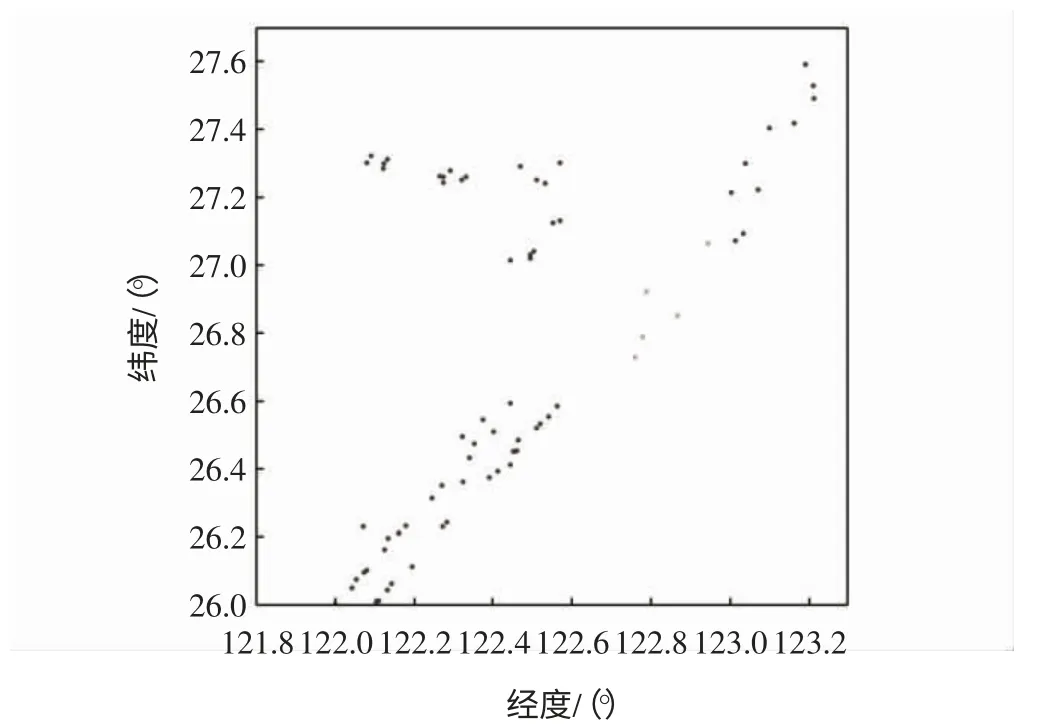
图6 三次样条插值法缺失点图Fig.6 Missing points by cubic spline interpolation

选取一个航班多次飞行的航迹点作为测试数据如图7（a）所示，从中去掉一部分点作为缺失点用来评估三次样条插值算法的性能，得到如图7（b）的点迹图，其中，方框表示去掉的航迹点。

应用三次样条插值算法后得到的对比图如图8所示。其中，“×”表示应用三次样条插值算法得到的缺失点位置，“·”则表示正常航迹点位置。

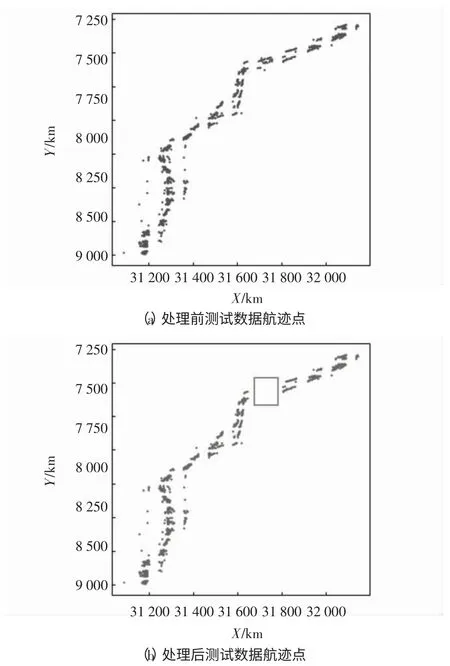
图7 选取的样本点图Fig.7 Sample point diagram

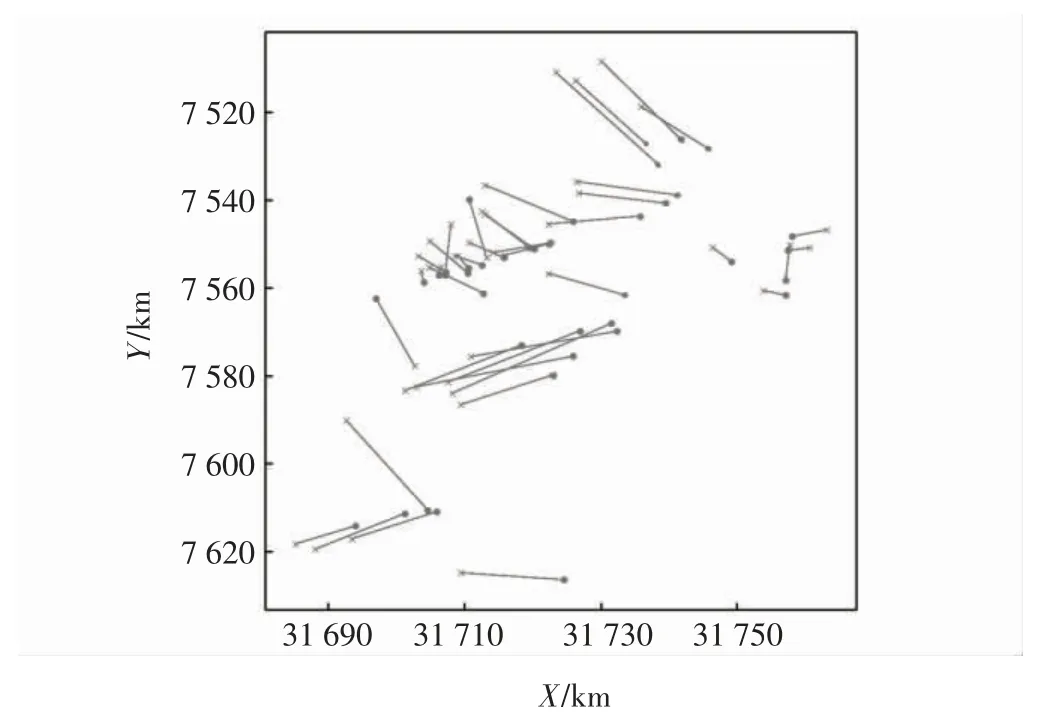
图8 算法得到的缺失点与原正常点对比图Fig.8 Missing points obtained by algorithm vs.original normal points

均方根误差对一组测量中较大或较小的误差非常敏感，能够很好地反映测量的精度，其表达式如下

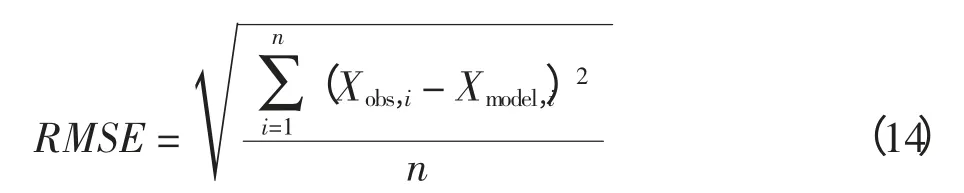
其中：Xobs，i表示观测值，即实验中利用三次样条插值算法得到的缺失点的值；Xmodel，i表示原始值，即数据集处理前的航迹点的值。

将三次样条插值算法与其他常用的插值算法，如线性插值算法、二次样条插值算法、拉格朗日插值算法[15]通过多次实验进行性能对比，同样以均方根误差作为评估标准，得到的结果如图9所示。

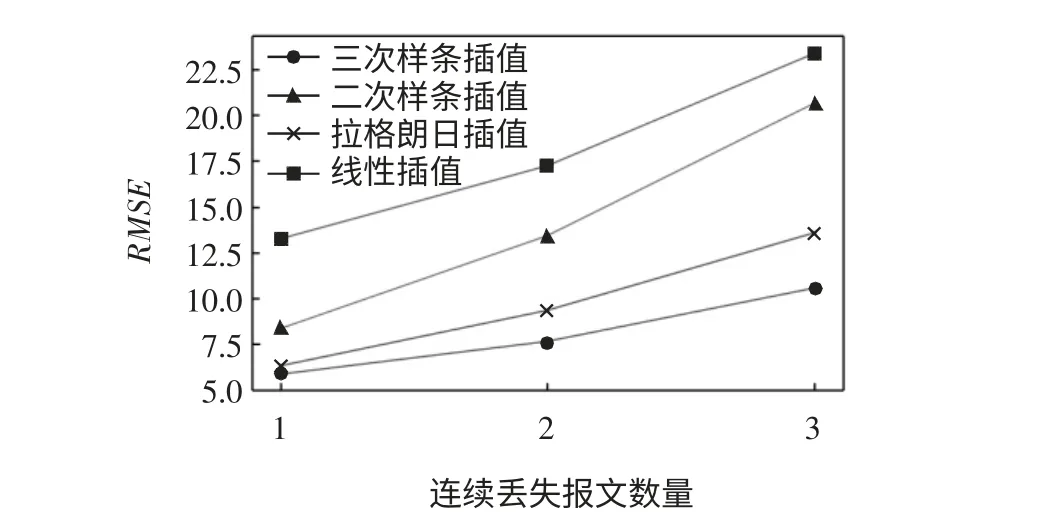
图9 不同插值算法性能对比图Fig.9 Performance comparison of interpolation algorithms

从图9中可看出：插值算法处理的连续丢失报文数量越多，产生的误差越大。在相同时间间隔下三次样条插值算法在性能上要优于其他几种算法。

3.2 盲区位置概率分布

实验所用航空公司的所有航班中共有两个航班出现位置报告缺失情况，按照上述方法得到的航迹点覆盖区域和缺失区域，取两个航班的并集，得到的结果，如图10所示。其中，“×”点表示重构缺失点，其余代表其他航班点的点迹，最终将两个航班得到的平行四边形缺失区域取并集得到总缺失区域。

基于高斯核函数的SVM 分类算法得到的盲区位置概率分布图如图11所示，其中，带宽σ 的取值为评估区域的短边长，经过坐标转换后得到σ=85。

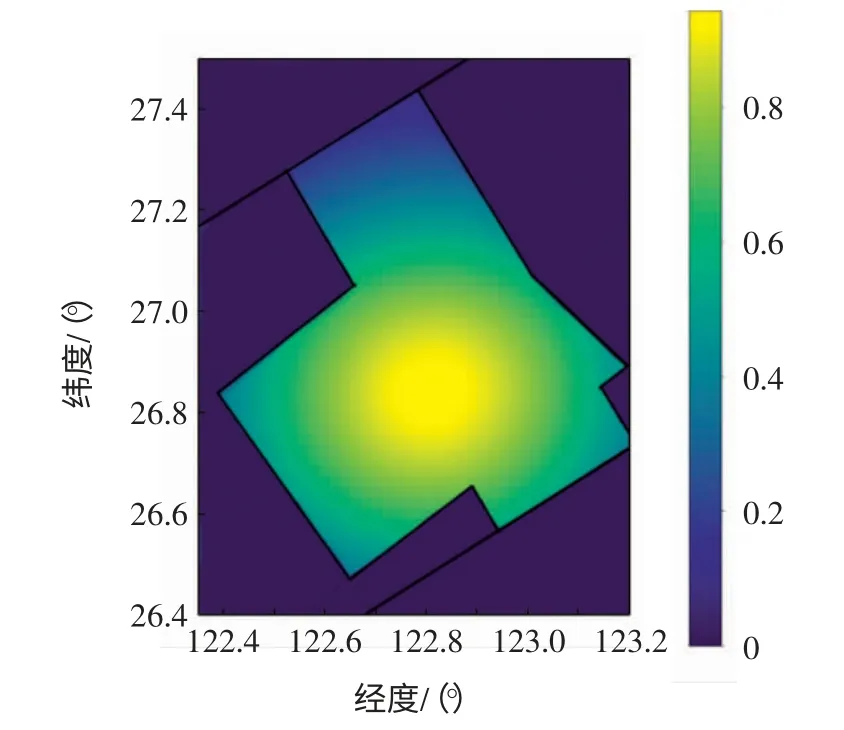
图11 ACARS 数据评估区域盲区位置概率分布Fig.11 Probability distribution of statistical assessment blind spots by ACARS

同理应用ADS-B 数据经过上述步骤也可得到相应的盲区位置概率分布图，如图12所示。

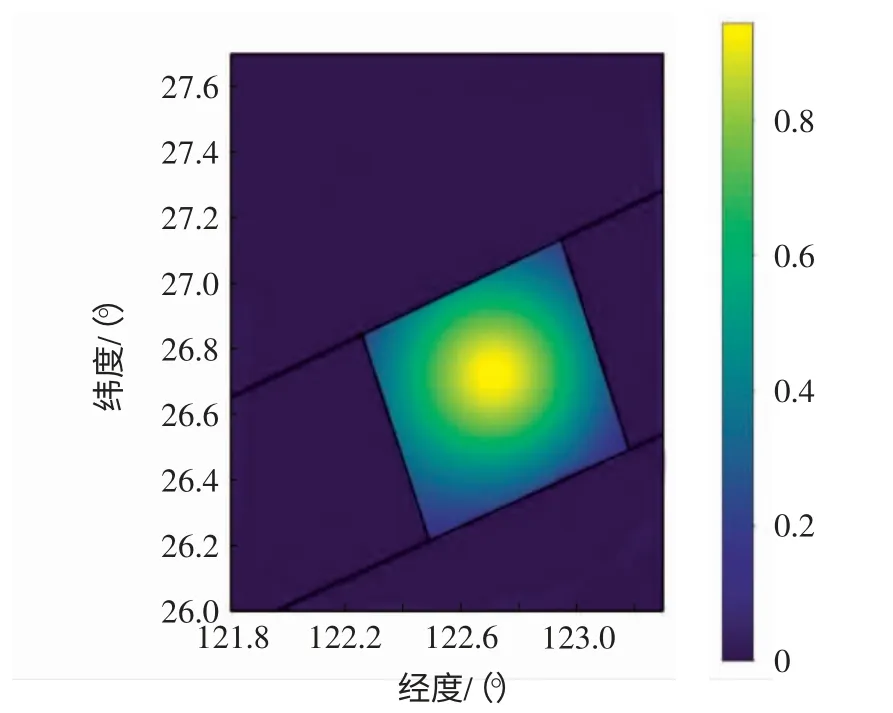
图12 ADS-B 数据评估区域盲区位置概率分布Fig.12 Probability distribution of statistical assessment blind spots by ADS-B

为了验证模型结果的正确性，选用一组相同航线的追踪数据作为测试数据（来自航班追踪网站VariFlight）。

首先，将测试数据进行预处理，将测试数据应用三次样条插值算法得到缺失值，得到的全部测试数据代入缺失区域的每个网格中，得到每个网格的缺失率，最终误差率为所有网格误差率的平均值，即

其中：MRi为测试得到的每个网格的缺失率；Pi为通过模型得到的网格的盲区概率。所用的测试数据包括原始数据和插值数据共10 000 余条，落入缺失区域的测试数据共7 848 条，以ACARS 数据划分的缺失区域为例，得到的缺失分布图如图13所示。

图13 缺失分布图Fig.13 Missing distribution

为了避免落入网格样本点过少而产生较大误差，去除落入样本点过少的网格得到的值。因此，图13中可以看到部分网格中没有数值，有数值的网格主要集中在航迹点覆盖区域的中部，最终按式（15）得到的误差率对比如表1所示。

表1 两种异构数据误差对比Tab.1 Error comparison of two kinds of heterogeneous data

算法的误差主要来源于三次样条插值算法带来的插值位置偏差，从数据对比可以看出，周期更短的ADS-B 数据在进行插值运算时产生的误差更小，因此，最终盲区分布产生的误差更小。

综上所述，模型对于两种多源异构数据都有不错的效果，但更适用于周期更短、数据量更大的数据，如ADS-B 数据。数据模型的优点在于计算简洁、运算速度快；缺点在于抗噪性较差，噪声点主要来源于非盲区原因而产生的位置报告缺失点。

4 结语

通过研究航班追踪盲区评估算法，基于多源异构追踪数据，建立航班追踪盲区评估模型。应用三次样条原理对缺失数据进行插值，然后将评估区域进行预处理，基于高斯核函数的SVM 分类原理对缺失区域内部每个位置进行盲区概率计算，将所有的影响值叠加得到区域的概率分布图中，最后通过两种常用的多源异构数据ACARS 数据和ADS-B 数据对模型进行测试，证明了算法模型的可行性。该模型在实际应用中对航空公司、局方开展航班追踪性能评估工作提供有益的借鉴。