无人驾驶车辆机场廊桥下动态避撞路径规划

王丙元，郑 芳，李 霞，姜 建，杨 搏

（中国民航大学电子信息与自动化学院，天津 300300）

近年来，无人驾驶技术发展迅速，多领域陆续有试验性项目落地。随着机场客流量不断增加，高效运营变得越来越复杂，据Airport Technology 报道，根据国际航空运输协会（IATA）调查，以往在空侧（如泊位引导区、货运区）发生的事故大多是由疲劳驾驶等人为因素导致的[1]，无人驾驶车辆的使用有望改变这种局面。2017年，戴高乐机场投放两辆无人车并进行了公开测试，效果良好。目前，无人摆渡车也陆续在机场投入试运行，可以预见，无人驾驶车辆必将最先在特定区域的路径下得以应用。机场廊桥下道路类似于无信号交叉口，且廊桥旁有遮挡物，出现车辆交汇的情况多，易发生拥堵碰撞等不安全情况，因此，为保证作业车辆安全行驶，提高机场运行效率，开展廊桥下无人驾驶作业车辆避撞研究具有广泛的研究价值和应用前景。

机场廊桥下避撞属于交叉口避撞问题。针对交叉口避撞问题，Alejandro 等[2]提出了合作交叉口控制方法，当主导车辆经过交叉口时，跟踪所控制车辆轨迹，可在避免碰撞的同时增加交叉口车流量，但该方法仅使用单车道行驶，未涉及车道变换情况。Qing 等[3]提出一种基于排的动脉多模态信号在线控制，提高了无信号交叉口的交通效率，但所使用的混合整数线性程序增加了算法复杂度，未能很好地解决交叉口时间最小化问题。Aoude 等[4]将支持向量机算法和贝叶斯滤波算法相融合（SVM-BF），通过采集周边车辆信息，实现避让危险车辆的目的，但基于概率的避撞算法存在随机性和通信延迟等问题，限制了无人驾驶在开放场景下的应用。Borenstein 等[5]提出向量场直方图算法，在多障碍物环境中规划出局部较优的运动方向，但未考虑障碍物尺寸及车辆运动学特性，不能满足实时避撞要求。动态窗口法（DW）虽能在线实时规划路径，具有良好的避障能力，满足动态环境下的自主导航要求，但不能实现全局最优[6]。RRT 算法[7]在进行路径规划时无需对环境进行具体建模，对场景有很好的适应性，并能够在短时间内搜索出一条或多条折线路径，但无法满足部分路径弯曲半径的要求，不符合工程实际要求。Wang等[8]提出的快速扩展随机树（RRT,rapidly-random trees）与动态窗口相结合的算法，仅考虑静态障碍物，且单向RRT 搜索时间过长，无法应用于机场特定实际场景。

在复杂多变的真实环境中，无人驾驶车辆在全局规划的给定路径下行驶时，会受到随机动态障碍物的影响，此时需采用局部避障方法安全行驶。首先在已有研究方法基础上，建立车辆运动学模型，然后利用双向快速扩展随机树（Bid-RRT，bidirectional rapidlyexploring random trees）算法与动态窗口融合算法，实现动态约束下的无人驾驶车辆避撞。该方法利用Bid-RRT快速搜索避障路径，提高路径规划效率，同时使用动态窗口法进行局部避障路径的平滑。通过模型仿真验证该方法在机场特定路径下的车辆动态避撞性能的有效性。

1 双向快速扩展随机树（Bid-RRT）跟踪算法

RRT 是一种基于采样的路径规划算法[9]。该算法通过构建递增类型，将规划空间起点作为根节点，在空间中随机增加叶节点，生成随机扩展树，直至随机叶节点到目标节点的值小于设定阈值为止。Bid-RRT算法是RRT 的一种改进形式，分别从起点和终点各生成一棵快速扩展随机树，采用启发式连接两棵树，双向并行、相向生长直至相遇，具有随机扩展效率高、收敛速度快的特点。算法流程如图1所示，Ta、Tb分别是从路径规划起点、终点出发要扩展的随机树，xrand是随机树在自由空间随机选取点，xnew是随机扩展的新节点。

如图2（a）所示，从指定起始点A、B 开始，Bid-RRT算法在空间中并行相向搜索，A、B 之间的距离小于设定的相遇阈值时两棵树在O 点相遇，其图中曲线为从A、B 出发的双向快速扩展随机树，路径AO、BO 分别为从起点和终点出发的规划路线；图2（b）中AB 曲线为Bid-RRT 算法规划出的路径，该路径折线段出现频繁且冗余线段较多。

图1 Bid-RRT 算法流程图Fig.1 Bid-RRT algorithm flow chart

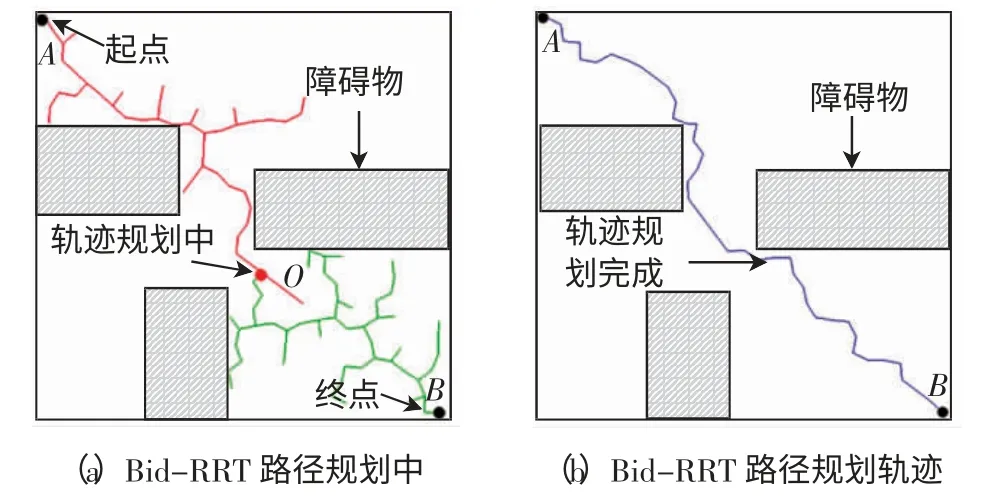
图2 Bid-RRT 路径规划轨迹Fig.2 Bid-RRT path planning track

2 动态窗口法

自主避障的动态窗口方法，通过在指定空间内搜索最佳指令，使目标函数取最大值，该算法路径规划速度快，能实时进行动态路径规划，且获得的路径更加平滑[10]。使用动态窗口法需建立车辆运动学模型。

2.1 车辆运动学模型

规划无人驾驶车辆运动避撞路径，需建立无人驾驶车辆运动学模型，以满足行驶过程中的运动学约束。由于车辆地面运动过程复杂，为保证算法的实时性，作如下约束和近似。

考虑机场环境下车辆低速行驶（货运10～20 km/h），将车辆简化到一个二维平面，车辆转向运动模型和车辆转向过程[11]，如图3和图4所示。图3中：（Xr，Yr）和（Xf，Yf）分别为车辆后轴和前轴轴心坐标；φ 为车辆航向角；δf为前轮偏角；vr为车辆后轴中心速度；vf为车辆前轴中心速度；L 为轴距。图4中：R 为后轮转向半径；P 为车辆瞬时转动中心；M 为车辆后轴轴心；N 为前轴轴心。

图3 车辆运动学模型Fig.3 Vehicle kinematical model

图4 车辆前轮转向示意图Fig.4 Vehicle front wheel steering diagram

在后轴行驶轴心（Xr，Yr）处，速度为

前后轴运动学约束为

联合式（1）和式（2）得

由前后轮几何关系得

将式（3）和式（4）代入式（2），得航向角速度为

其中：w 为车辆航向角速度。同时，由w 和车速vr得转向半径R 和前轮偏角δf为

由式（3）和式（5）得车辆动力学模型为

运动学模型进一步被简化为

2.2 速度采样

由无人驾驶车辆运动模型，利用采样的多组速度数据轨迹推算。在速度（v，w）二维空间中，根据车辆和周围环境限制，车辆最大最小速度限制[9]为

其中：v 为车辆行驶速度；w 为车辆旋转速度。由于无人驾驶车辆受到力矩限制，存在最大加速度，因此在车辆轨迹前向模拟的一个周期内，存在一个动态窗口，且该窗口内车辆的实际速度为

其中：vc、wc为车辆当前速度和旋转速度；为车辆当前最大加速度和最大减速度；Δt 为车辆轨迹前向模拟周期。

考虑到无人驾驶车辆安全行驶问题，为避免碰撞，根据制动距离，求得速度范围[12]为

其中：a 为加速度，dist（v，w）为速度（v，w）对应轨迹上离障碍物最近的距离。

无人驾驶车辆传感器检测到的最小障碍物距离在二维空间中不连续，为保证评价函数的连续性，需进行如下归一化处理，即

其中：h 为方位角评价函数；n 为所有采样轨迹个数；i为当前待评价轨迹。

2.3 评价函数

评价函数评价轨迹优劣。评价函数[12]为

其中：α、β、γ 分别为方位角、轨迹距障碍物距离、速度函数的权重；σ 为平滑函数。

表1～表3分别给出了不同权值下的规划所需时间、最小安全距离和车辆最小速度。

表1 不同α 时的实验对比Tab.1 Experimental comparison with different α

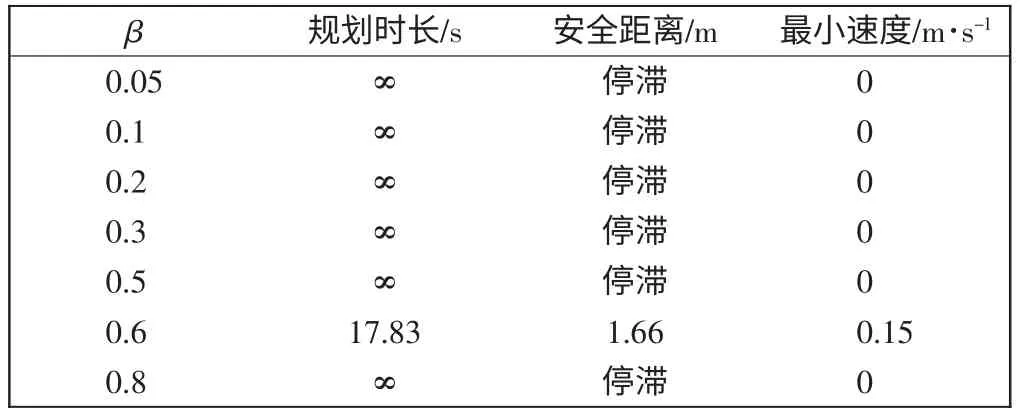
表2 不同β 时的实验对比Tab.2 Experimental comparison with different β

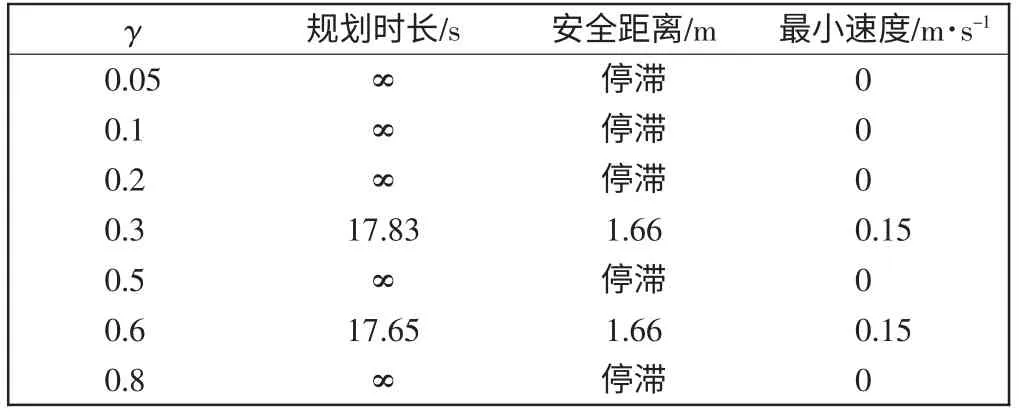
表3 不同γ 时的实验对比Tab.3 Experimental comparison with different γ

图5为不同权重和前向模拟时间p 下的轨迹，图中起点为（0，0），终点为（10，10）。图5（a）中，α=0.6，0.8 时，运行轨迹时间分别为52.47 s、56.51 s，运行时间较长。图5（b）中，β=0.2，0.8 时，运行轨迹在遇到相邻较近障碍物时停滞不前。图5（c）中，γ=0.8 时，安全隐患较大；γ=0.1 时，遇到障碍物停滞不前。障碍物是动态随机的，随着前向模拟时间p 的推移，模拟时仿真结果显示轨迹可能未触碰障碍物，但实际车辆行驶时轨迹可能已触碰障碍物。图5（d）中，p=6 时，最后规划出的实际轨迹（轨迹2）触碰了障碍物；当p =1，前向模拟时间太小，探索次数增多，导致规划出的路线（轨迹3）过长。折衷考虑选取p=3。综上结果表明，当α=0.1，β=0.6，γ=0.3，p=3时，所得规划轨迹较为合理。

图5 不同权值下的评价函数轨迹Fig.5 Evaluation function trajectories with different weights

图6为动态窗口局部避障轨迹，考虑车辆障碍物大小，以障碍盒型式给出优化避障轨迹。避障路径如图6（a）所示。图6（b）为避障采样轨迹，利用评价函数对多组轨迹进行评价，得到最优路径，图中不同数字曲线表示不同轨迹。利用动态窗口法规划局部路径虽平滑性好，但存在局部最小问题。

图6 动态窗口局部轨迹Fig.6 Local trajectories of dynamic window

3 动态窗口与Bid-RRT 的融合算法

Bid-RRT 算法虽能快速规划出全局路径，但搜索路径为折线段，不满足实际工程需求，动态窗口进行动态路径规划，规划路径平滑，但易陷入局部最小。将二者融合，在提高路径规划负率的同时改善了路径平滑性。动态窗口与Bid-RRT 融合的方法如图7所示。首先由Bid-RRT 规划出一条无冲突的动态避障全局路径，然后将全局路径信息、车辆运动模型和来自传感器的障碍物信息发送到动态窗口规划器中，进行局部路径规划，最后规划出带避障功能的优化平滑路径。

图7 融合算法规划Fig.7 Fusion algorithm planning

融合算法寻优路径如图8所示，图8（a）为规划过程，图8（b）为在Bid-RRT 全局规划基础上采用动态窗口法通过速度采样和正则化处理，规划出的一条平滑路径。可见二者融合可实现动态避障路径优化。

图8 融合算法寻优路径Fig.8 Optimization path of fusion algorithm

4 机场特定场景下的路径规划

汇流冲突和交叉冲突是造成交叉口交通事故和拥堵的主要原因。由于两种情况避撞方式相同，以汇流冲突避撞为例。采用Prescan 搭建机场廊桥下作业车辆交通场景，视廊桥下作业路径为丁字路口，完成地图构建，如图9所示。地图各坐标位置如表4所示。1 号车辆为主导车辆，2 号车辆为障碍车辆。将融合算法应用于廊桥下作业车辆避撞。设定主车辆1 在丁字路口场景下得起始位置A 和终点位置B，由Bid-RRT 和动态窗口法规划出一条从起点到终点的无碰撞最优路径。

图9 机场廊桥下车辆作业道路图Fig.9 Vehicle operation road map under airport bridge

表4 地图各位置坐标Tab.4 Position coordinates on map

考虑实际场景车辆大小，仿真设置障碍盒，将车辆当成圆的内切四边形，以圆的半径作为评价函数的约束条件，同时考虑导入仿真地图与Prescan 搭建地图的比例，选取的无人驾驶车辆运动学模型参数和轨迹评价函数参数如表5所示。

表5 融合算法输入参数Tab.5 Input parameters of fusion algorithm

机场廊桥下丁字路口动态避障轨迹如图10所示。轨迹可看出，融合算法规划路径较为平滑，规划时长较RRT 算法缩短27.2%，路径长度减少14.7%。与PRM相比，规划时长缩短69.2%。

图10 不同算法机场廊桥下丁字路口动态避障轨迹Fig.10 T-shaped intersection dynamic avoidance trajectory under airport bridge

在机场廊桥特定路径下，选取RRT、Bid-RRT、PRM、Bid-RRT 与动态窗口融合算法所得的规划时长与路径长度的10 组轨迹数据求平均值，如表6所示。

表6 不同规划路径方法规划时长及路径长度Tab.6 Planning duration and path length of four methods

表6中数据表明，融合算法规划的路径较平滑，规划时长较RRT 算法缩短40.3%，路径长度较Bid-RRT算法减少6.7%。与PRM 相比，规划时长缩短72.2%。

5 结语

针对机场空侧廊桥下特定路径，无人驾驶车辆交汇情况多，易发生碰撞的问题，提出双向快速扩展随机树与动态窗口融合算法，进行无人驾驶车辆的路径规划，保证作业车辆的安全动态避撞。仿真结果验证了算法的有效性，得到以下结论：①Bid-RRT 执行双向搜索指令，提高了收敛速度；②动态窗口算法由采样速度推算轨迹，使轨迹更平滑；③在全局路径基础上融合动态窗口进行局部规划避障，实现了动态障碍物的避撞。融合算法的平均避障路径规划时长和路径平滑度都优于RRT 算法、Bid-RRT 算法和PRM 算法。该方法亦可应用于类似场景下的车辆避撞及动态路径规划。