妙用斜边中线定理

谭炜东

由平行四边形的性质“平行四边形的对

角线互相平分”和矩形的性质“矩形的对角线相等”，我们可以得到这样一个定理：直角三角形斜边上的中线等于斜边的一半，这个定理揭示了直角三角形斜边上的中线与斜边之间的数量关系.同时由它可知，斜边上的中线把直角三角形分成了两个等腰三角形.利用这个定理解证一些几何题时，往往可以化难为易、化繁为简，收事半功倍之效.

一证明两线垂直

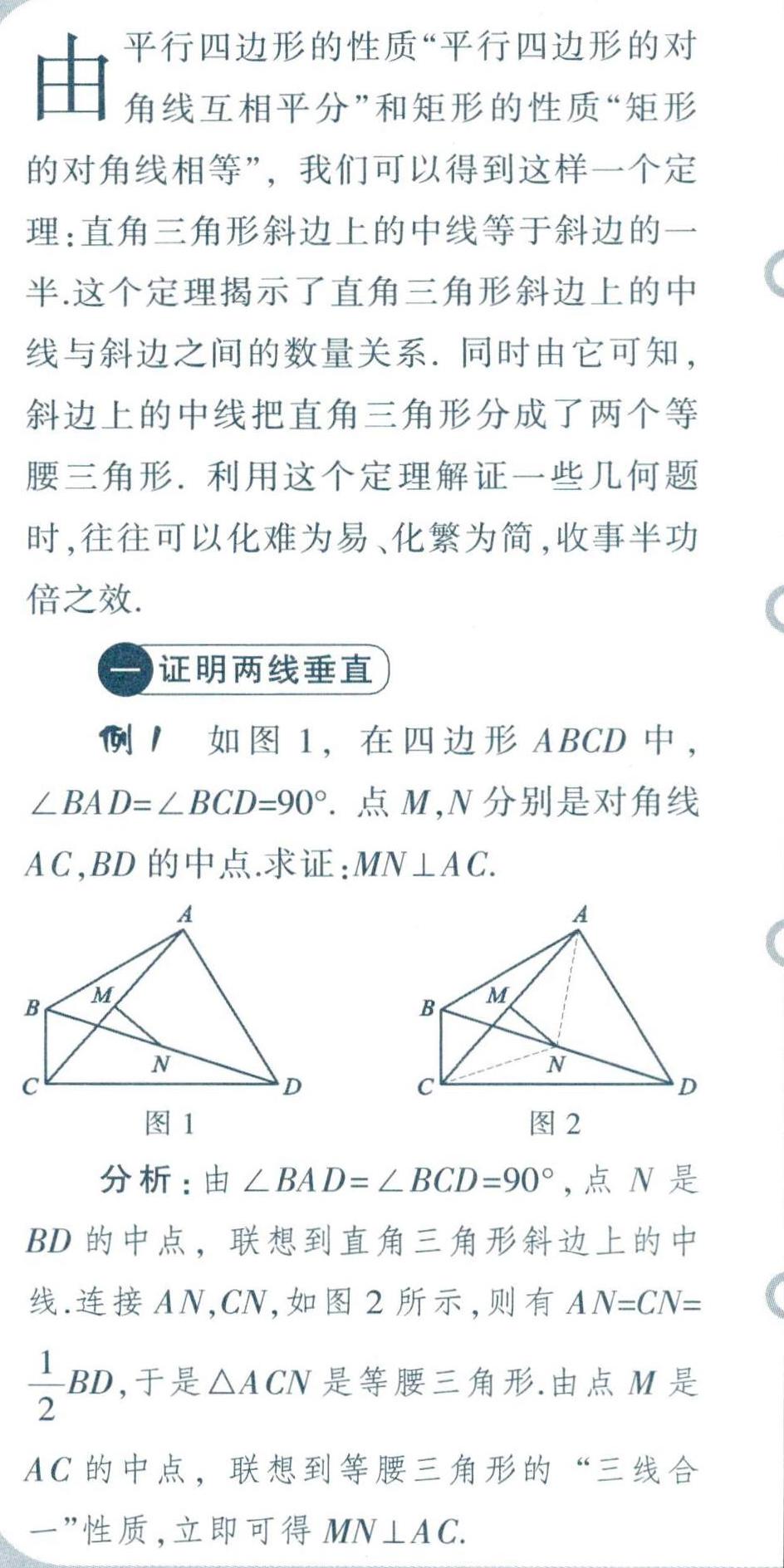
例1 如图1，在四边形ABCD中，∠BAD=∠BCD=90°.点M，N分别是对角线AC，BD的中点.求证：MN⊥AC.

分析：由∠BAD=∠BCD=90°，点N是BD的中点，联想到直角三角形斜边上的中线.连接AN，CN，如图2所示，则有AN=CN=1/2BD，于是△ACN是等腰三角形.由点M是AC的中点，联想到等腰三角形的“三线合一”性质，立即可得MN⊥AC.

二判断四边形的形状

例2如图3，在□ABCD中，过点A，C分别作对角线BD的垂线AE，CF，垂足分别为E，F点M，N分别为AB，CD的中点，连接ME，MF，NE，NF.试判断四边形EMFN的形状，并说明理由.

分析：由点M，N分别为AB，CD的中点，AE，CF都垂直于BD，根据直角三角形斜边中线定理可以得到ME=1/2AB=MB，NF=

21/2CD=ND，故∠1=∠4，∠2=∠3.由四边形ABCD是平形四边形，得AB//CD，AB=CD，所以∠2=∠4，ME=NF.于是∠1=∠3，ME∥NF.故四边形EMFN是平行四边形，

三证明线段相等

例3如图4，点E，F分别为正方形ABCD的边AB，BC的中点.DF与CE相交于点P，连接AP.求证：AP=AD.

分析：要证AP=AD，如果想利用∠ADP=∠APD，结合已知条件，这种思路几乎行不通.注意到点E为边AB的中点，AD//BC，我们自然想到延长CE交AD的反向延长线于点Q，如图5所示，易证△AEQ≌△BEC，故AQ=BC=AD，即AP为△DPQ的DQ边上的中线.结合待证结论“AP=AD”，只需证明∠DPQ为直角即可，即证∠2+∠3=90°.易证△BEC≌△CFD，所以∠1=∠3.于是，只需证∠2+∠1=90°.这显然成立，从而结论得证.

需要说明的是，数学上的很多定理都是有一定的前提条件的，直角三角形斜边中线定理也是如此，运用这个定理的前提条件是这个三角形是直角三角形，结论则是斜边上的中线等于斜边的一半，而不是直角边上的中线等于直角边的一半！

牛刀小试

如图6.△ABE和△CDE有一個公共顶点E.若∠AEB为直角，AB=CD，且AB，CD互相平分于点O，求证：∠CED为直角.

（答案在本期找）