圆环形压电振子疲劳仿真分析与实验研究

田晓超，王海刚，王 虎,吴 越，张思达,杨志刚

(1.长春大学 机械与车辆工程学院，吉林 长春 130022;2. 吉林大学 机械与航空航天工程学院，吉林 长春130025)

0 引言

由压电材料构成的压电振子具有变形精度高,速度快,体积小,无磁干扰等特点，常被作为高速、高精度的驱动源使用[1]。压电驱动机构的疲劳损坏或失效主要表现为压电振子的疲劳破坏。针对构成不同驱动机构及工作状态的压电振子，其失效形式也不同。因此，有必要对压电振子的疲劳破坏及工作寿命进行研究。

国内外相关学者针对压电振子疲劳破坏已进行了相关研究。Mizuno M 等[2]建立了疲劳寿命公式和损伤变量方程表示为静态断裂强度、疲劳极限和平均值的函数，损伤理论与实验结果比较验证了方法的有效性。M. Okayasu等[3]在5 kHz高频率下对压电陶瓷位移和裂纹扩展进行了测试，表明位移强度与扩展速率与声呐强度间存在线性关系。Mamoru Mizuno等[4]通过在各种载荷频率下对压电陶瓷进行压缩-疲劳试验，阐明了陶瓷表面的损伤机理。Mitsuhiro Okayasu等[5]研究了锆钛酸铅(PZT)的力学性能和疲劳破坏特性。Weon-Pil Tai等[6]研究了PZT极化处理和晶体结构对断裂韧性和抗疲劳性的影响。而国内学者主要针对膜片式压电振子进行疲劳仿真、建立模型及实验方法的研究[7-13]。

针对圆环形压电振子疲劳破坏问题，本文主要对其疲劳特性进行了研究，通过仿真分析和疲劳试验对用其构造的压电驱动机构疲劳使用寿命预测具有一定的指导意义。

1 结构组成与振动方式

图1、2分别为圆环形压电振子结构和实物图。环形压电陶瓷贴置在金属基板上，中间圆孔部位用于连接传振机构，通常可分为单晶片和双晶片振子。

图1 压电振子结构示意图

图2 压电振子实物图

圆环形压电振子一般为陶瓷片直径小于金属基板直径，采用周边固定支撑方式。将压电振子施加交变驱动信号时，压电陶瓷会发生收缩与膨胀，进而促使振子上、下振动，形成周期性往复运动，从而驱动系统工作，其变形示意图如图3所示。

图3 压电振子变形示意图

2 压电振子疲劳仿真分析

2.1 静力学分析

表1为选用的压电陶瓷材料。

表1 压电陶瓷材料参数

压电材料的压电矩阵和刚度矩阵为

(1)

109(N/m2)

(2)

图4为压电振子的尺寸结构。图中，b1为压电陶瓷内径，b2为基板内径，压电陶瓷直径a1=48 mm，金属基板直径a2=66 mm，陶瓷厚h1=2.1 mm和基板厚h2=1.5 mm。

图4 压电振子尺寸结构示意图

利用ANSYS/Multiphysies模块建立模型。金属基板材料选用65Mn，陶瓷材料选用SOLID5单元类型，金属基板材料采用SOLID45单元类型。边界条件限定压电振子环形基板边缘9 mm固支。得到前四阶振动模态如图5所示。

图5 压电振子前四阶模态云图

由图5可知，一阶模态符合压电振子工作模式。设定金属基板上电压为0，压电陶瓷表面电压为180 V。将所有应力集中一个方向上，仿真结果如图6所示。

图6 压电振子等效应力云图

由图6可以看出, 压电振子最大受力为86.479 MPa，远小于材料的屈服极限(108 MPa)，可认为压电振子在静力状态下不会发生疲劳破坏。

2.2 压电振子疲劳分析

将仿真疲劳计算数值进行激活，预设循环次数Np=4.67×109时，计算结果如表2所示。最大受力点结果如图7所示。

表2 不同节点处计算结果

图7 最大受力点获取示意图

在节点编号为10 023处的最大应力为86.47 MPa，循环次数为5.001×109。从压电振子实用性考虑，预设6个月循环次数Np=4.67×109(180×24×3 600×300=4.67×109)。最大应力节点疲劳耗用系数小于1，可认为压电振子不会发生疲劳破坏。

由表2可看出，危险节点的疲劳耗用系数均小于1，如果压电振子最大应力节点处不发生疲劳破坏，则认为整个压电振子不会发生疲劳破坏。此次预设压电振子6个月循环次数，认为在这种情况下压电振子有很好的疲劳强度。

3 结构参数对疲劳特性影响

3.1 金属基板材料影响

选取金属基板材料为65Mn、不锈钢、铝合金3种材料，令电压U=160 V，a1=48 mm，a2=66 mm，h2=1.5 mm，h1=2.1 mm，得到单、双晶片振子的疲劳相关数据，实验结果如表3所示。

表3 不同金属基板材料单双振子疲劳参数

由表3可看出，基板材料为65Mn的抗疲劳性能最好，且双晶片振子要比单晶片振子疲劳寿命长。

3.2 陶瓷与基板直径影响

保持压电陶瓷与基板直径比不变，分析压电振子疲劳性能随不同压电陶瓷的直径变化情况，结果如图8所示。由图可看出，随着直径的增大，循环次数呈下降趋势，表明压电陶瓷的直径越大，整个振子的疲劳寿命越短。但直径不能太小，否则振子的性能会受影响，因此，需要综合考虑各项指标来选择振子的直径尺寸。

图8 疲劳寿命受压电陶瓷直径变化曲线图

3.3 驱动电压影响

保持其他参数不变，改变驱动电压幅值，疲劳性能曲线如图9所示。由图可看出，压电振子循环次数随电压幅值的增加而下降，当驱动电压超过190 V时，压电振子未达到预定的循环次数，认为疲劳强度不能满足要求。因此，需合理选择驱动电压。

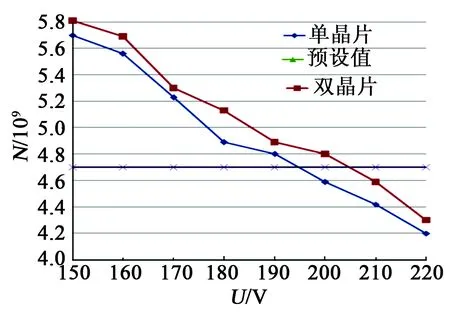
图9 不同电压下振子疲劳寿命曲线图

3.4 陶瓷与基板厚度影响

保持h1/h2=1，其他参数不变，压电陶瓷与基板厚度对疲劳性能的影响，如图10所示。由图可知，疲劳寿命随着陶瓷和基板厚度增大而不断加强。双晶片压电振子陶瓷与基板厚度均小于0.18 mm，单晶片压电振子陶瓷与基板厚度均小于0.23 mm时，压电振子未达到预定的循环次数，强度不能满足要求。

图10 陶瓷片厚度对振子疲劳寿命曲线图

综上分析可知，金属材料65Mn的抗疲劳性能最好；压电振子双晶片型比单晶片型抗疲劳性强；驱动电压的幅值影响较大；陶瓷及基板直径和厚度对振子的疲劳寿命有一定影响。因此，选用强度较高的基板材料，合理增加振子厚度，选择合适的驱动电压幅值，无特殊情况下选用双晶片型振子，对提高压电振子的使用寿命具有重要意义。

4 压电振子疲劳实验

4.1 实验方法与装置

表4为本文选用的压电振子参数。通过对一批相同结构参数压电振子施加相同的驱动频率，对比压电振子的抗疲劳性能，并从实用性的角度对其作出可靠性分析。

表4 振子参数列表

实验步骤:

1) 取20个尺寸参数一致的压电振子样品，分别编号，测定每个振子的输出力和输出位移，每个测量数据测量3次取平均值。

2) 将20个压电振子分为4组，每组5个，按每组压电振子施加电压为160 V、170 V、180 V、190 V、200 V进行疲劳试验。测试时间为3个月，记录每天振子输出力和位移。

3) 计算各压电振子试件试验前后输出力和输出位移的差值，统计相关压电振子的失效个数，算出其下降比。根据GB1772-79《电子元器件失效率试验方法》，评判此次疲劳试验的失效率、置信度及可靠性。

图11为输出力测试图。图12为输出位移测试图。

图11 输出力测试图

图12 输出位移测试图

4.2 实验结果分析

表5为实验数据测试结果。由图可看出，有3个振子在实验前后振子的性能均相差20%以上，破坏的振子都是施加了190 V、200 V高电压，而电压低于190 V的振子暂时未达到疲劳破坏的标准，可见承受高电压的振子更易发生疲劳损坏。

表5 失效振子性能统计表(共20个振子)

将失效的压电振子制作驱动器样机，与未发生疲劳损坏压电振子制作的样机进行比较，如图13所示。由图可看出，用损坏振子制作的样机比正常振子制作的样机输出能力低，可见振子的性能优劣直接影响驱动器的输出性能。压电振子在高电压状态下工作易表现出疲劳特性，其性能也明显下降，进而影响驱动器的输出性能。

图13 压电驱动器驱动能力对比图

此次压电振子振动循环实验预设为90天，除3个振子性能下降外，其他都未达失效标准。正常压电振子工作时间为90×24=2 160 h，性能下降程度最大的振子工作时间为62×24=1 488 h，此时其驱动电压为190 V和200 V。可以预测，如果在低驱动电压下其使用寿命更长。因此，从压电振子实用性和可靠性的角度分析，此批压电振子可达到使用要求。

5 结束语

利用ANSYS软件对圆环形压电振子进行了静力学和疲劳寿命研究，分析了不同结构参数对圆环形压电振子疲劳寿命的影响。结果表明，金属材料65Mn的抗疲劳性能最好；振子直径和厚度变化对其疲劳寿命影响较大；压电振子双晶片型比单晶片型抗疲劳性强；高电压、高应力会降低振子的疲劳寿命。对压电振子进行了疲劳寿命实验，从振子可靠性和实用性角度分析，选取的此批振子完全能达到使用要求。