分层多子群协作正余弦算法及应用

赵永奇，邹 锋，陈得宝，姜子琪，康佳惠

（1.淮北师范大学 物理与电子信息学院，安徽 淮北 235000；2.淮北师范大学 计算机科学与技术学院，安徽 淮北 235000）

原始正余弦算法(sin cosine algorithm，SCA)[1]是一种新型的群智能优化算法，相比于粒子群优化算法、差分进化算法、遗传算法等传统优化算法，正余弦算法具有结构简单、参数少、易于实现等优点，一经提出便引起了研究人员的关注。并且相关改进的算法可以应用到各种实际问题中，如调度问题[2]、图像分割[3]、旅行商问题[4]、电力系统优化[5]等问题。

原始正余弦算法在处理简单函数优化问题时，求解精度高，收敛速度也比较快。当需要优化的问题变得复杂、种群数量减少时，原始正余弦算法容易陷入局部最优解，使得算法过早收敛，求解精度变低。为了克服原始正余弦算法求解精度低、收敛过早的缺点，研究人员提出了众多的改进方案。Singh 等[6]利用正余弦算法和樽海鞘群算法相混合进行改进，提高算法的收敛性能；Tawhid 等[4]提出了一种离散正余弦算法，用来解决旅行商问题；Rizk-Allah[7]提出了一种基于正交并行信息的求解数值优化问题的SCA-OPI 算法。

针对原始正余弦算法后期收敛速度慢、局部搜索能力差的缺点，本文提出了一种分层多子群协作正余弦算法(hierarchical multi-swarm cooperative sin cosine algorithm，HMCSCA)。首先，在HMCSCA算法底层结构中，各个子群中的个体利用增加“提高阶段”的正余弦算法更新位置信息，并由各个子群中的最优解组成顶层种群。其次，在算法架构的顶层中，顶层种群利用全局最优个体信息和底层各个子群最优个体信息进行高斯采样实现种群信息的更新。最后，在一定迭代次数之后，利用随机重组策略打乱各个子群中的个体，保持种群多样性。

1 原始SCA 算法

SCA 算法是基于三角函数中正弦函数和余弦函数而建立的群智能优化算法，与传统群智能优化算法类似，SCA 通过随机生成一组解来启动算法的更新过程，利用目标函数对这些解进行评价，之后更新最优解，直到算法结束。更新方程为：

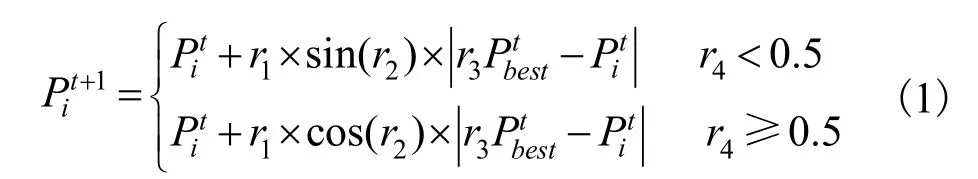
表1 SCA 算法步骤

2 分层多子群协作正余弦算法

分层多子群改进策略对算法性能的改进有明显的效果[8-9]，多子群机制能够使算法保持强劲的搜索能力，不至于过早地收敛从而陷入局部最优，可以提高算法的搜索精度。分层机制的加入可以提高算法的收敛速度。该算法改进方式被研究人员应用到多种算法的改进中[10-11]。

2.1 分层多子群策略

设计了双层多子群改进策略，结构如图1 所示。

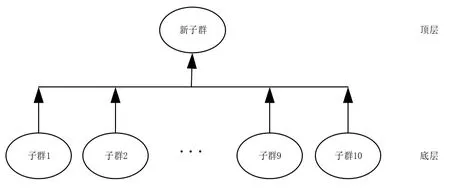
图1 双层多子群结构图

在这个架构中，算法由底层和顶层2 个部分组成。在底层中，将种群划分为10 个子群(子群1～子群10)，每个子群个体数目相等且相互独立，每个种群中的个体利用改进的正余弦算法进行更新。底层中子群更新结束之后，从各个子群筛选出最优个体组成顶层的新子群，新子群利用各个底层子群的最优个体与整个种群最优个体经高斯采样学习后更新新子群中位置信息。这样的进化机制，既可以保证种群的多样性，又能加快算法的收敛速度。

2.2 改进正余弦算法

为了提高正余弦算法的种群多样性和收敛速度，本文将对原始正余弦算法增加一个“提高阶段”[12]，该阶段利用不同个体之间的差异，提高种群的整体水平。“提高阶段”的更新方程为：

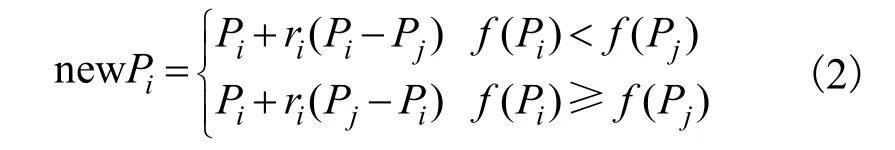
其中：f(p)表示p个体的适应度值，本文中以目标函数值作为适应度值。Pi表示第i个个体“提高”前的位置，Pj表示第j个个体“提高”的位置，且i≠j，ri为[0,1]之间的随机数，newPi表示个体“提高”后的位置。

改进正余弦算法通过评价函数的适应度值选择最优个体，如果f(newPi)＜f(Pi)，则用newPi替换Pi，反之则不变。

2.3 高斯采样学习

高斯采样学习作为在算法改进中常用的策略，被研究人员广泛应用于各类算法的改进中[13-14]。高斯采样学习可以对种群个体的位置进行扰动，在搜索前期能增强算法的探索能力，在后期能增强算法的开发能力。高斯采样学习的公式如下：

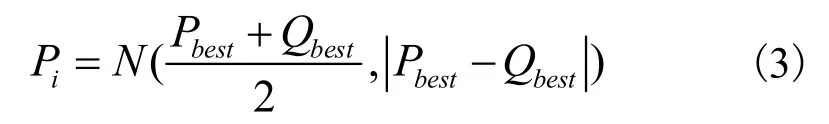
其中，Pbest为整个种群最优解；Qbest为子群最优解。

2.4 随机重组策略

HMCSCA 算法架构的底层中，由于种群被分成多个子群，且每个子群的个体数目很小，所以种群在迭代过程中很容易陷入局部最优。为避免这种情况的出现，HMCSCA 算法采用一种简单的重组方法，在该方法中，底层各个子群中的个体都要在一定次数迭代之后进行随机重组。随机重组的操作可以改变子群个体的位置信息，实现信息在各个子群之间交流，从而维持整个种群的多样性。

2.5 算法步骤

本文提出的分层多子群协作正余弦算法的寻优过程如下所示。

步骤一：设置算法的各项参数。

步骤二：初始化种群的位置，确定全局最优解。

步骤三：种群个体在底层结构中根据式(1)和式(2)进行更新。当新解优于当前解则保留新解，反之保留当前解。

步骤四：在底层结构中通过筛选底层结构中各子群中的最优个体组成新子群，新子群根据式(3)进行更新。当新解优于当全局最优解则保留新解，反之保留全局最优解。

步骤五：每五代进行一次随机重组。

步骤六：若当前评价次数FEs 小于maxFEs，则返回步骤三，否则迭代结束。

3 仿真实验分析

本文将进行2 组实验来验证HMCSCA 算法的性能，一组是将HMCSCA 算法和SCA 及其改进算法进行比较。另一组将HMCSCA 算法和其他优化算法进行比较。仿真实验将采用18 个有代表性的基准测试函数对算法的优化性能进行评估。

3.1 参数设置

本文所用的18 个函数来自文献[15]。其中，单峰函数F1～F4，多峰函数F5～F10，F11～F18 分别是F3～F10 的旋转函数。设定所有算法的种群个数m为40，以函数值为算法的适应度值，最大函数评价次数(maxFEs=5 000*dim)作为算法的终止准则。本文实验均在主频为3.2 GHz、内存为8 GB 的Win10操作系统下的MATLAB R2015b 软件上实现。

3.2 与SCA 及其改进算法的比较

为了验证新算法HMCSCA 与SCA 及其改进算法(ISCA[16]、ASCA-PSO[17]、BBNSCA[15]、SCA)之间的优劣，在测试函数10 维情况下进行实验。为了消除不确定因素带来的随机情况，每种算法独立运行20 次。表2 为实验所得的最优解(Best)、平均值(Mean)、标准差(Std)，其中表中粗体为最优值。由于部分基准函数的收敛曲线比较相似，图2为有代表性的收敛曲线。

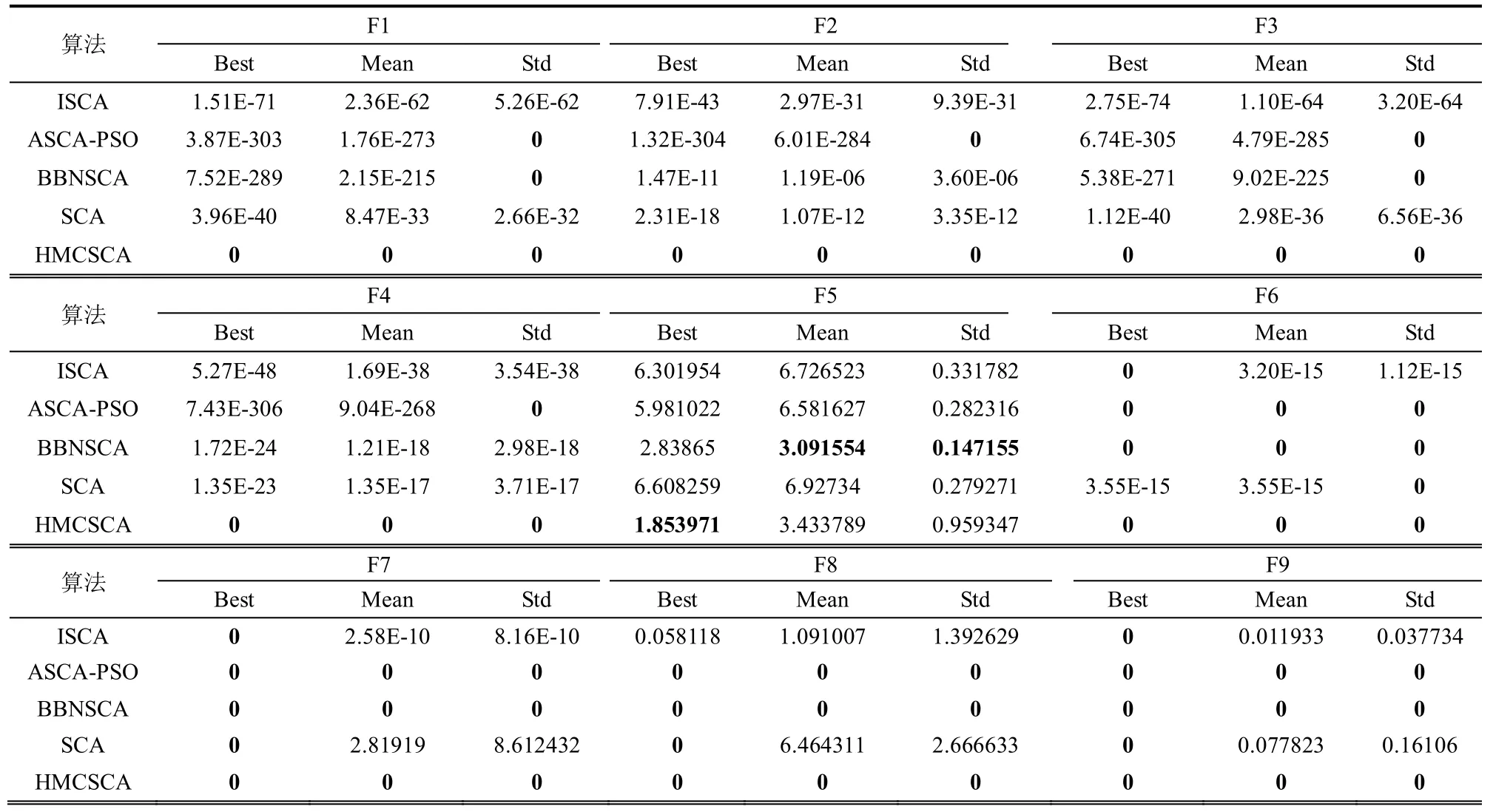
表2 10 维函数测试结果

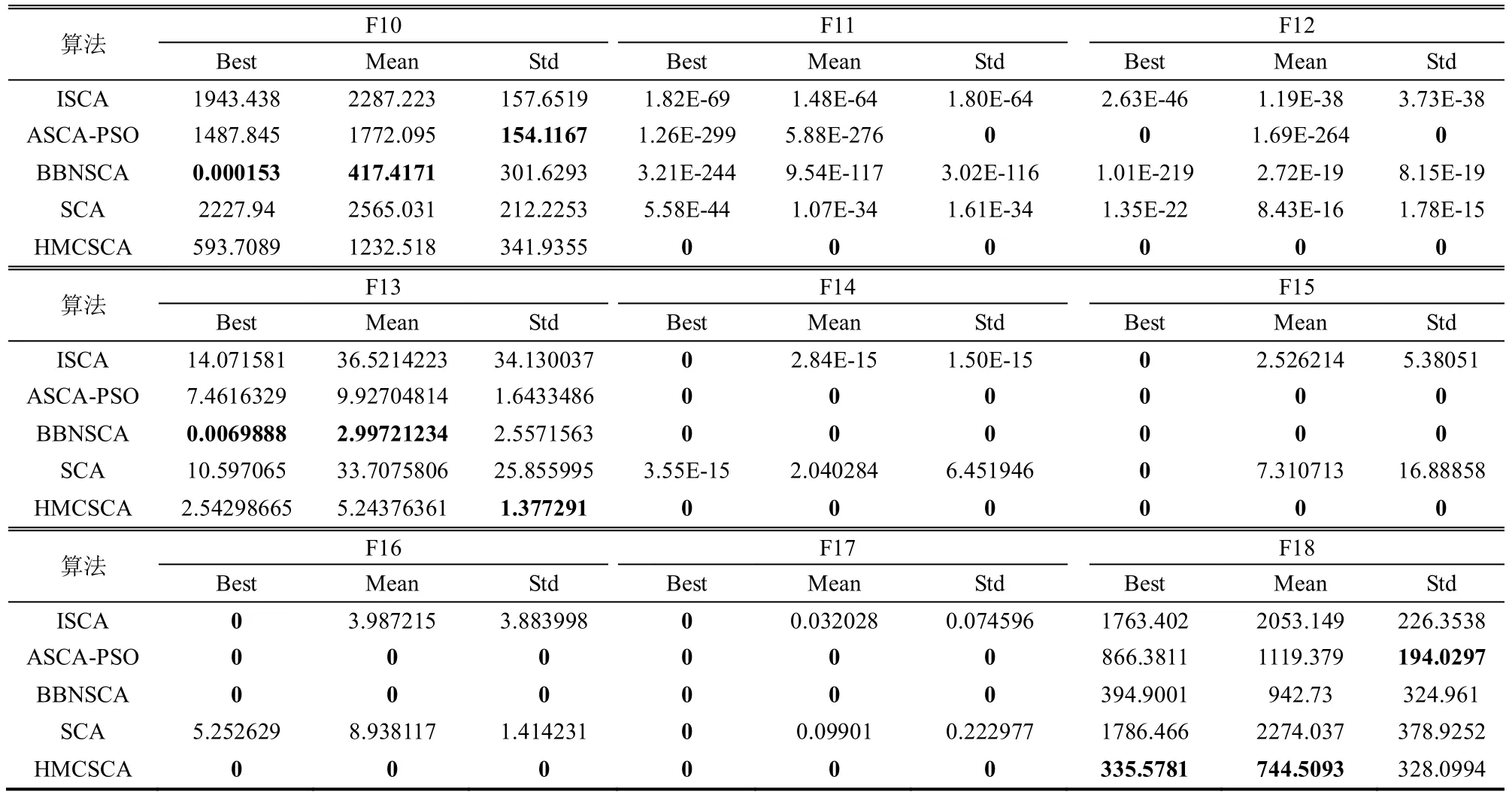
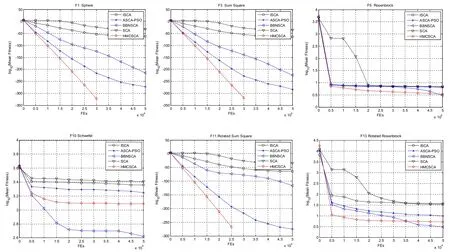
图2 10 维部分函数平均适应度值变化图

从表2 的数据和图2 的收敛曲线可以看出，HMCSCA 算法的性能明显优于SCA 算法，且HMCSCA 算法对18 个函数里面的F1～F4、F6～F9、F11～F12、F14～F17 等14 个函数收敛到理论上的最优解0。由表3 中的均值和标准差得知，HMCSCA算法对18 个测试函数的结果优于SCA 算法，表明改进策略对提高SCA 算法的求解精度和鲁棒性有着明显的效果。

相比于其他改进的SCA 算法，HMCSCA 算法在F1～F4、F11～F12 这6 个函数的求解的平均精度远远高于ISCA、ASCA-PSO、BBNSCA 算法，。而且标准差也达到了理论上的最小值，这说明HMCSCA 算法的性能稳定，鲁棒性较强。但是，无论是HMCSCA 算法还是其他改进的SCA 算法，都对F5、F10、F13 和F18 这4 个函数的优化结果较差，说明SCA 算法及其改进算法在优化类似漂移函数这样的复杂问题时性能需要加强。

3.3 与其他优化算法的比较

为了进一步验证HMCSCA 算法的性能，本次实验将 HMCSCA 算法于其他智能优化算法(BSA[18]、PSOFDR[19]、TLBO[20]、CBO[21])进行比较。数据统计方式同3.2 节。

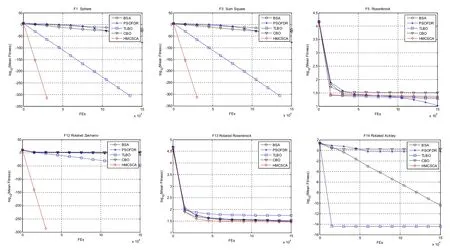
图3 30 维部分函数平均适应度值变化图

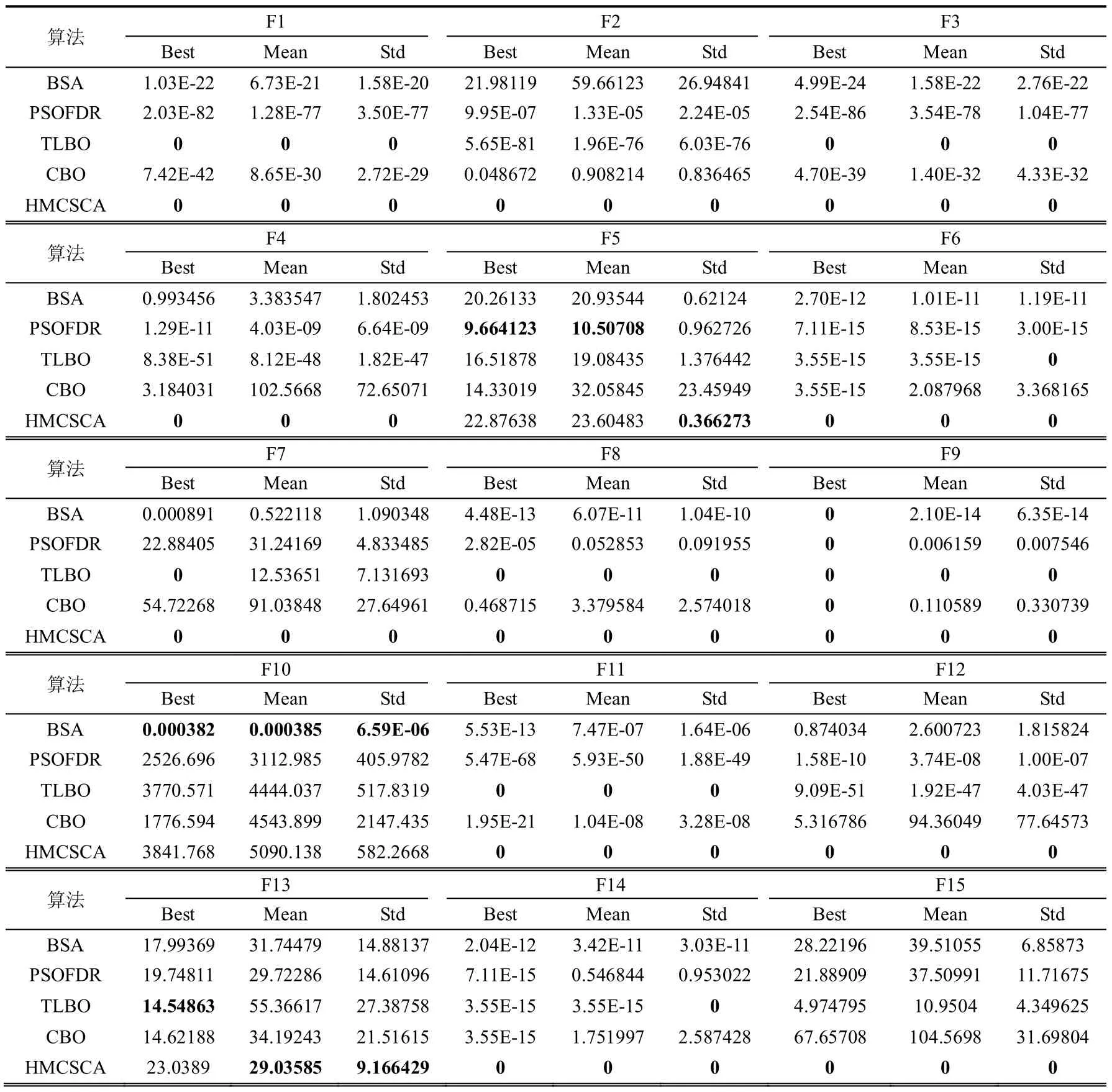
表3 30 维函数测试结果

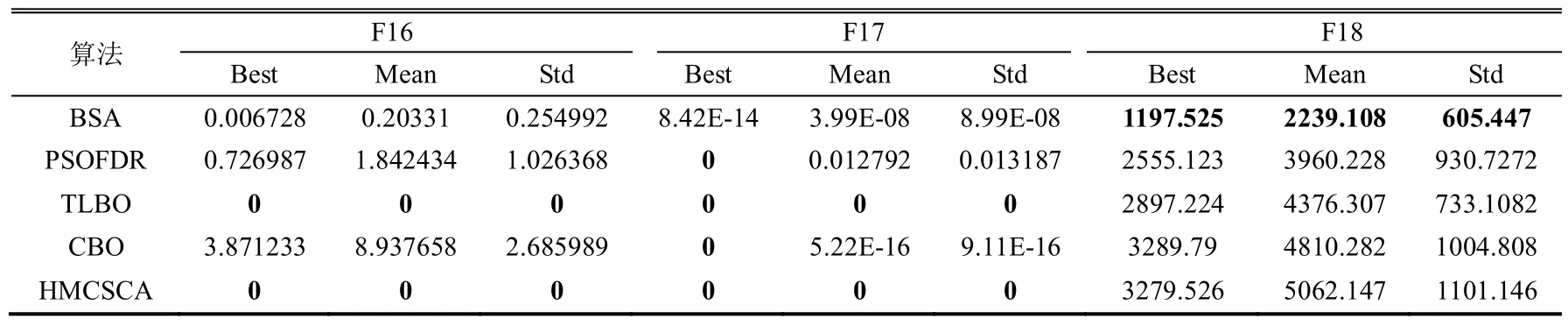
从表3 和图3 中得知，HMCSCA 算法于其他优化算法相比，在处理优化问题时的求解精度和收敛速度方面具有明显的优势。从最优解分析，HMCSCA 算法在F1～F4、F6～F9、F11～F12、F14～F17这14 个函数上优于BSA、PSOFDR、TLBO、CBO算法，且得到最优理论上的最优解，说明HMCSCA的求解精度优于对比算法。从平均值角度分析，HMCSCA 算法在F1～F4、F6～F9、F11～F17 这15个函数上的表现优于其他算法，且除F13 外，都达到了理论上的最优解。从标准差角度分析，F1～F9、F11～F17 这16 个函数上优于BSA、PSOFDR、TLBO、CBO 算法，且除了F5 和F13 2 个函数外，标准差都取得了理论上的最优解，说明HMCSCA算法具有较强的鲁棒性。

综合以上分析，HMCSCA 能获得比较好的优化性能，特别是在优化精度和鲁棒性方面，明显优于其他优化算法。其原因有两方面：一方面，在底层中，多子群策略可以实现各个子群中个体的信息交互，提高种群的多样性，避免算法陷入局部最优解。另一方面，顶层种群由底层各个子群的最优个体组成，在更新过程中，可以加快算法的收敛速度。仿真实验的结果说明分层策略和多子群策略相结合，对改进SCA 算法有明显的效果。但是HMCSCA以及其他SCA 改进算法在优化复杂的漂移函数时，没有表现出良好的性能，其原因大概是SCA 算法的框架不适合求解较为复杂的优化问题。

4 HMCSCA 在神经网络中的应用

人工神经网络[22-23]通过模拟人类学习的模式，逐渐被应用于非线性建模、模式识别和控制系统等应用领域。人工神经网络是一种能够识别输入、输出数据集之间关系的数学结构。由于其搜索空间是高维的、多模态的，所以很容易受到噪声或数据丢失的影响。因此，利用智能优化算法对人工神经网络进行优化的方法被研究人员广泛应用。

4.1 HMCSCA 进行神经网络训练

本文采用HMCSCA 算法训练的是一个三层前馈神经网络，图4 是该神经网络的基本结构[24]。

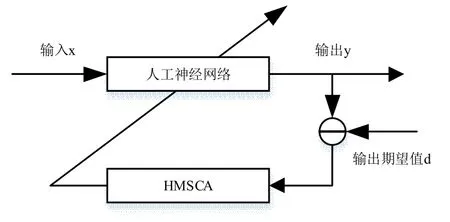
图4 基于HMCSCA 的ANN

输入连接到所有隐藏单元，这些隐藏单元依次连接到所有输出。变量由神经网络权重和偏差组成。在本文实验中，输入层中使用的激活函数是输入变量的线性组合，隐层中使用的激活函数是Sigma 函数，而输出层中使用的激活函数是隐层输出变量的线性组合。变量的范围设置为[-10，10]。假设一个具有M个输入单元、N个隐藏单元和K个输出单元的三层前馈神经网络结构如图5 所示,变量数目如下：

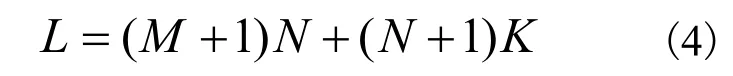
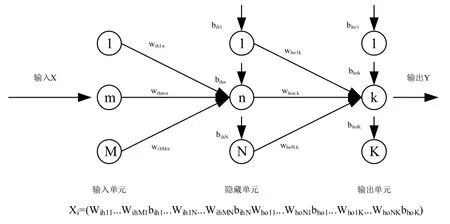
图5 人工神经网络的结构

对于神经网络训练，其目的是利用最小误差测度来训练一组权值。这里的目标函数是所有训练模式的均方误差之和(mean sum of squared errors，MSE)[25]。

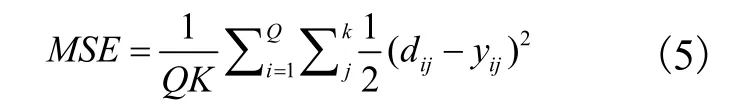
其中，Q是训练数据集个数，K是输出单元的个数，dij是期望输出，yij是由神经网络推断出来的。

4.2 非线性函数逼近

对于给定的单输入单输出非线性函数(SISO)的逼近[24]：

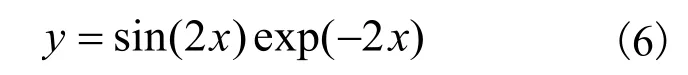
在这个实验中，通过一个包含1 个输入单元、5 个隐藏单元和1 个输出单元的三层前馈人工神经网络系统，以构建一个单输入单输出非线性系统y=f(x)实现对式(6)的建模。

该人工神经网络的变量数为16 个，由此得知，每个变量维度为16。为了训练该人工神经网络，从实际模型中选取了620 对数据。在本次实验中，算法的种群个数设定为40 个，终止条件为最大评价次数FES=25 000。实验结果如表4 所示，其中加粗数据为最优解，误差变化曲线如图6 所示。

表4 SISO 数据表

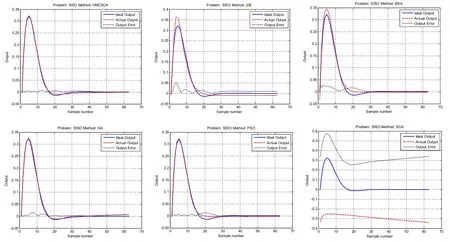
图6 SISO 误差变化曲线图

由表4 中的数据和图6 的误差变化曲线图得出，HMCSCA 算法在处理SISO 时，HMCSCA 的各项性能远远优于SCA 算法。相比于jDE，GA，PSO，BSA 算法，HMCSCA 算法在求解精度和鲁棒性方面，依然有优势。

4.3 非线性系统辨识

对于给定的多输入单输出非线性系统(MISO)，如式(7)所示：

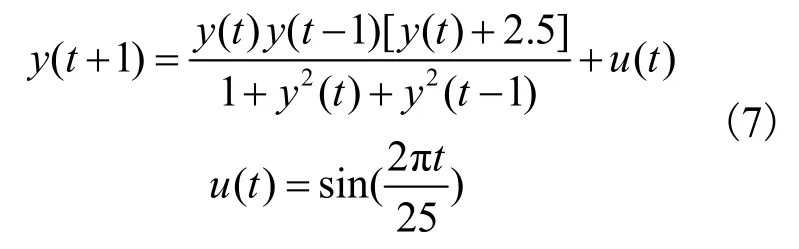
在这个实验中，通过一个包含3 个输入单元、5 个隐藏单元和1 个输出单元的三层前馈人工神经网络系统，构建如下的多输入单输出非线性系统[24]以实现对式(7)的建模：

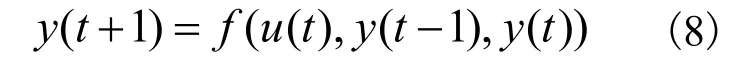
该人工神经网络的变量数为26 个，所以决策空间的维度为26。为了训练神经网络，从实际模型中选取了100 对数据。在本次实验中，算法的种群个数设定为 40 个，终止条件为最大评价次数FES=25000。其实验结果如表5 所示，误差变化曲线如图7 所示。

表5 MISO 数据表

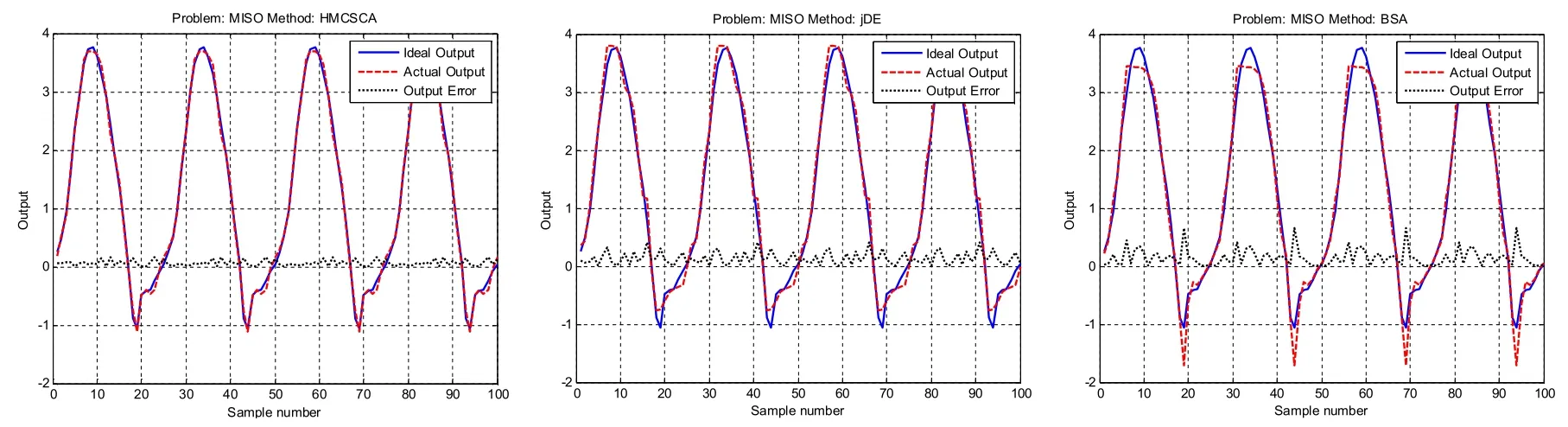
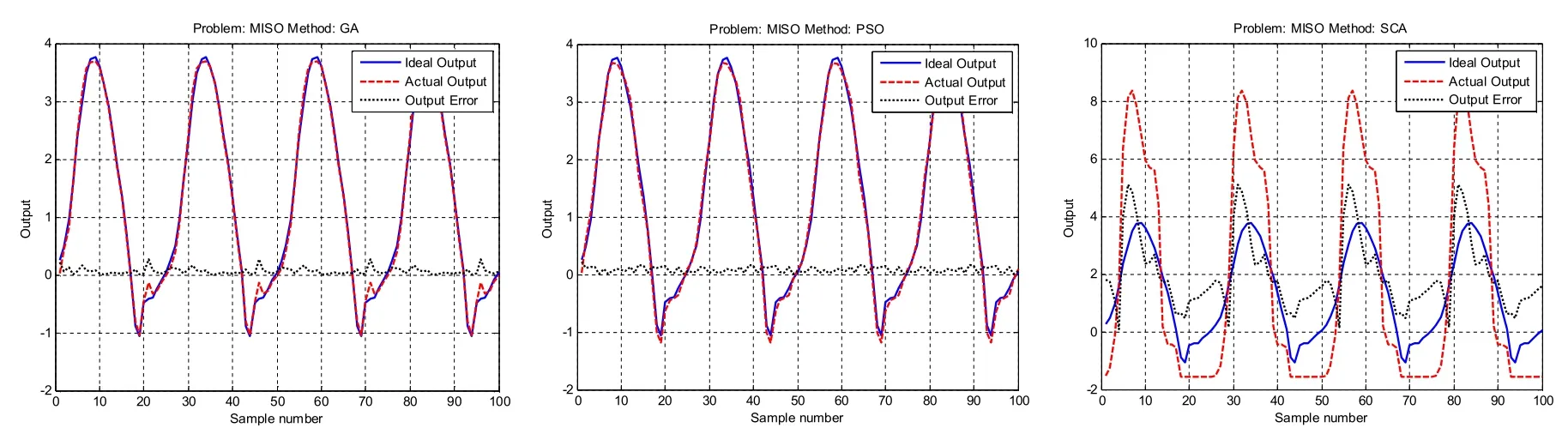
图7 MISO 误差变化曲线图

由表5 中的数据和图7 的误差变化曲线图得出，SCA 算法在处理MISO 时，优化结果比较差，性能远不如HMCSCA 算法。从均值可知，HMCSCA在求解精度方面优于jDE，GA，PSO，BSA 算法。对表5 中的标准差进行分析可得出，HMCSCA 的鲁棒性不如其他四种对比算法。

综上所述，在处理SISO 时，HMCSCA 算法的求解精度和鲁棒性优于其他对比算法。在处理MISO 时，HMCSCA 算法的求解精度优于其他算法，但是在鲁棒性方面不如jDE、GA、PSO、BSA算法。

5 结束语

本文提出一种分层多子群协作正余弦算法，该算法能够实现探索阶段和开发阶段的平衡，提高求解精度和收敛速度。通过18 个基准测试函数和在神经网络中的应用的实验结果表明，HMCSCA 算法在收敛性以及稳定性方面优于SCA 算法以及其他对比算法。但是，在处理类似漂移函数等复杂问题时，与对比算法比较并没有良好的表现，这也为SCA 算法的下一步改进指明了方向。