焦炉集气管压力状态空间建模与多模型预测控制

刘昕明，吕 亮，王 威

（1.辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105；2.中国航天科工集团公司 第三研究所,北京 100013）

焦炉集气系统是一个复杂的MIMO 系统，具有多变量、非线性、强耦合等特性，难以建立精准的数学模型[1]。由于焦炉集气系统分析与设计的需要，希望能够建立满足基本工程要求的近似模型[2-3]。此外，由于焦炉生产工作于3 个不同的典型工况，目前采用单一的控制律很难获得理想的控制效果。本文根据焦炉集气管压力现场工艺特点，将焦炉生产划分为3 个相对独立的工况：结焦初期落煤、结焦中期和结焦周期末期。首先在集气管压力系统机理分析的基础上建立非线性模型，然后非线性模型在每个工况的平衡点进行线性化，分别展开成线性状态空间子模型。根据获得的集气管压力系统的多个线性子模型，再运用基于状态空间的广义预测控制算法设计控制器，多工况之间的切换采用柔化的切换策略。最后以某焦化厂为背景，利用现场数据建立模型，并将本文方法与单模型预测控制情况下的控制效果进行了仿真对比。

1 焦炉集气管压力系统建模

某焦化厂JB8 型焦炉有两座焦炉和4 段集气管，如图1 所示。P1、P2、P3、P4分别为4 段集气管内荒煤气压力；分别为集气管蝶阀后的荒煤气压力；Ps1、Ps2、Ps3、Ps4分别为两座焦炉内碳化室底部压力，受到装煤、提导套以及煤气发生量的影响；Q1、Q2、Q3、Q4为两座焦炉上升管的煤气流量；P5为引风机吸力；P6为主管道压力；P6是引风机的机前吸力；Ps5为用户和化工处理段的煤气压力。在这里暂不考虑对其的控制，认为其始终满足控制要求[4]。

将整个系统看做连通容器，则管道的阻力系数为气压对管道流量的导数；对象的容量系数为管道容积对管道压力的导数。

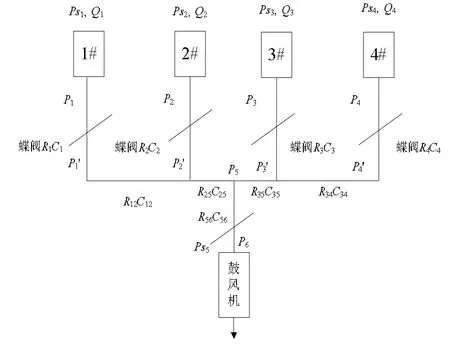
图1 焦炉集气系统结构图

根据管道阻力系数与容量系数的关系，可得dQ=Cdp/dt，由输入与输出平衡有：dQ=Q入-Q出，结合焦炉系统机构，可建立集气系统动态方程如下：

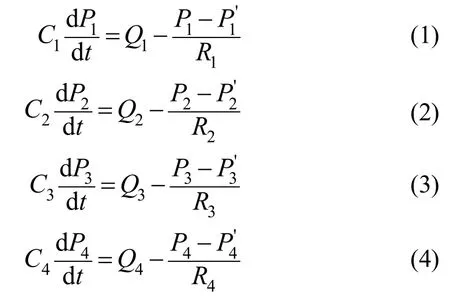
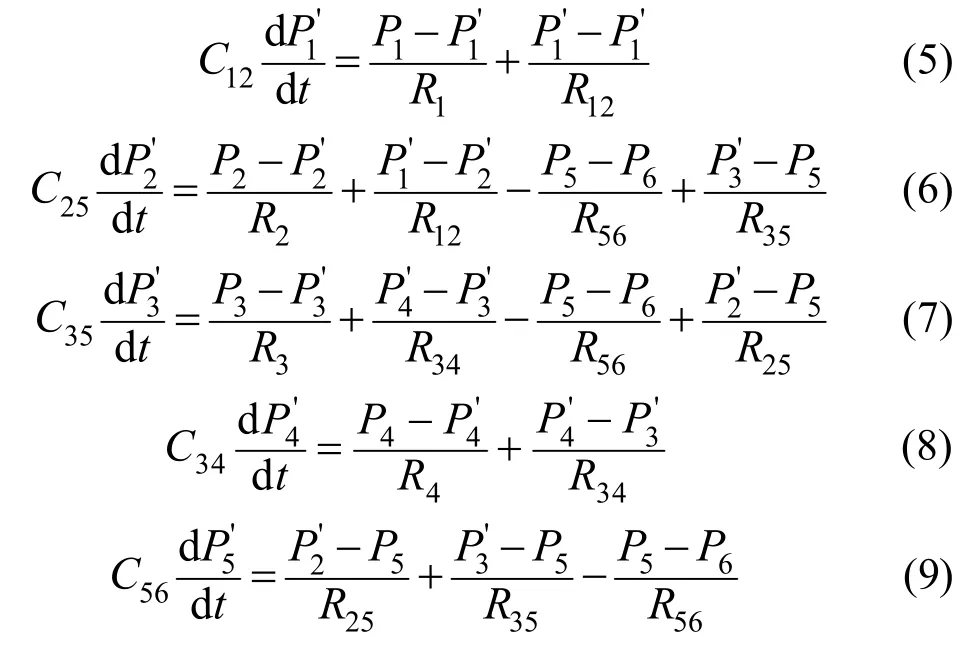
其中，R1、R2、R3、R4是蝶阀的阻力系数，R12、R34是管道阻力系数，管道阻力系数可以看作是常量。如果忽略环境因素的影响，流量与压力的关系为。那么荒煤气发生量则取决于碳化室底部压力Ps与荒煤气及其压力P[5-7]：。可以看出上述动态平衡方程是非线性方程。

将焦炉集气过程分为3个典型工况，找到每个工况的平衡点，将公式(1)-(9)的焦炉集气管压力机理模型，进行非线性方程在3个平衡点处线性化：

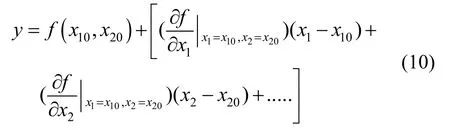
忽略二阶以上的项得，Δy=k1Δx1+k2Δx2，其中，。

设焦炉集气管压力的稳定工作点为P1=P10，P2=P20，P3=P30，P4=P40，P5=P50，P6=P60，Ps1=Ps10，Ps2=Ps20，Ps3=Ps30，Ps4=Ps40，R1=R10，R2=R20，R3=R30，R4=R40，在上述平衡点处线性化，集气系统动态平衡方程变为：

式中：Y为4 段集气管压力，U为阀门开度，则状态方程的参数，可以按如下形式表示：

2 基于状态空间的多模型预测控制

对于线性模型状态空间表达式

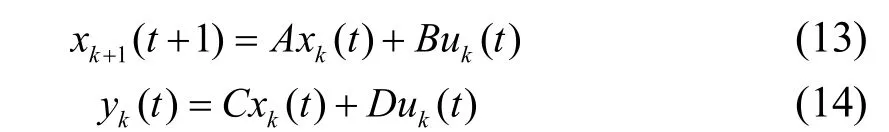
其中，A∈Rn×n，B∈Rn×m，C∈Rl×n，D∈Rl×m，为状态模型常系数矩阵，xk∈Rn×l为状态向量，uk∈Rm×l为模型输入，yk∈Rl×l为模型输出，根据预测控制原理，预测未来j步的最优系统输出为[8]：

其中，j=1,2,...,N1，预测时域为N1，控制时域为Nu，Nu步以后，控制量不再变化。写成矩阵形式有：

其中，

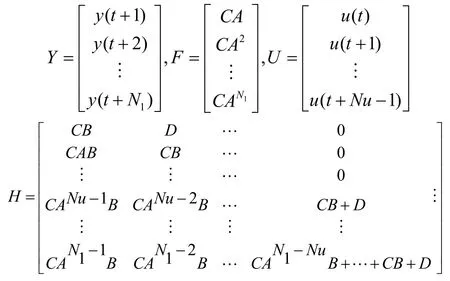
x（t）为状态向量，优化函数取为：

将（16）式代入（17）式中得到显式控制律：

焦炉集气管压力非线性模型在不同的工况下，可以近似线性化为多个线性子模型。在检测到工况变化信号后，根据工艺要求，压力设定值也发生变化，为了保证系统稳定，本文选择柔性切换方法[9]。控制过程中，多个控制器同时运行。假设系统在k0时刻切换模型，当k≤k0时，系统模型为M1；当k0＞k时，系统模型为M2；系统状态距离模型M2平衡点的均方差统计为μ。

3 仿真验证与分析

3.1 焦炉集气管压力系统不同工况选取

集气管压力的主要影响因素是焦炉装煤与换向加热，据此将焦炉生产过程中集气管压力分成3个典型工况：落煤工况下，煤从高处落下，给碳化室带来很大的冲击，此外新煤水分比较多，高温蒸发使得压力骤然升高；结焦周期中段工况，煤处于干馏状态，压力波动主要来自于末端，集气管压力总体相对稳定；结焦周期末断，煤已经变成焦炭，产生气体变少，压力减少。

3.2 焦炉集气控制系统参数选择

管道阻力系数ξ与容量系数Cv的关系如下：

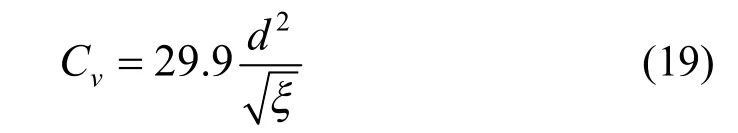
其中，d为蝶阀的内径，ξ是管道的阻力系数。

根据上述分析，根据现场数据得到焦炉集气管压力系统在3 个不同工况下的平衡点。根据本文建立的集气管压力模型，以上参数和平衡点代入(12)式，得到不同工况子模型。根据不同工况参数，对集气管压力控制系统在3 个工况模型的情况下进行仿真。

利用上面得到的数学模型，分别对装煤、装煤间歇、换向3 个工况进行验证。装煤特征主要体现在装煤扰动上，设1#焦炉装煤扰动为ΔPs1，观察各集气管压力输出变化。装煤间歇工况以及换向工况下的模型特性通过施加蝶阀阶跃ΔR1验证。最后利用多模型预测控制方法[9]验证模型的动态特征。

图2 装煤工况下施加装煤扰动ΔPs1各集气管压力曲线

图2 装煤工况下施加装煤扰动ΔPs1后，集气管1 受到影响压力急剧升高，装煤结束后，压力回落，与其相邻的2 号集气管压力由于耦合的影响也相应升高，其它集气管由于距离1 号集气管较远，受到的影响较小。

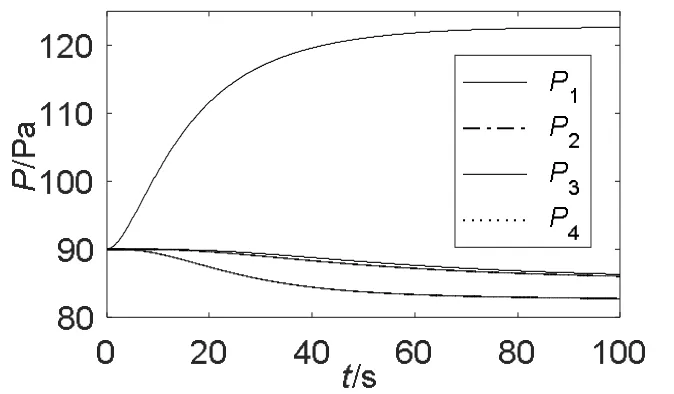
图3 装煤间歇工况下施加蝶阀阶跃ΔR1各集气管压力曲线

图4 换向工况下施加蝶阀阶跃ΔR1各集气管压力曲线

装煤间歇工况中施加ΔR1作用，由于1#集气管出气量减小，而其它相邻集气管受分配到的吸力增加，因此压力下降，如图3。换向工况模型中仍施加ΔR1作用，但是由于吸力降低压力变化幅度和速度都比装煤间歇工况缓和，如图4。

实际生产过程中，落煤属于结焦初期，接下来依次是结焦中期工况和结焦末期工况。为了验证本文控制算法，在仿真过程中前140 s 为落煤工况，中间160 s 为结焦中期；后100 s 为结焦末期。仿真结果如图5 和图6 所示。

图5 可看出本文方法超调量更小，尤其在第一种落煤工况下较为明显。将数据归一化，求得偏差平方值积分（IAE），对比结果如表1 所示，采用本文方法，在所有3 种工况下均比单一模型预测控制的控制误差小。

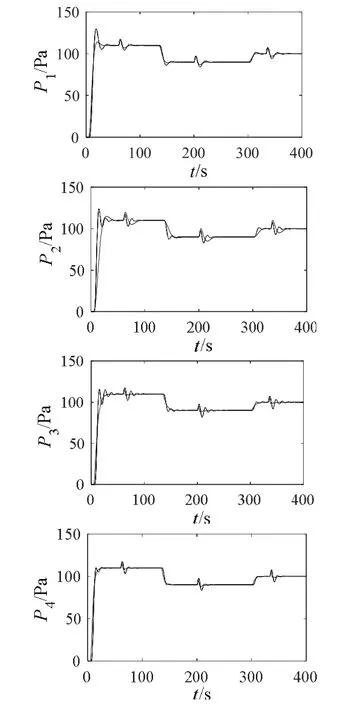
图5 阶跃扰动下多模型预测控制与单模型预测控制的系统输出对比曲线

表1 阶跃扰动下两种控制策略下IAE 指标对比

将图6 中随机扰动下的系统数据归一化，求得偏差平方值积分（IAE），对比结果如表2 所示。

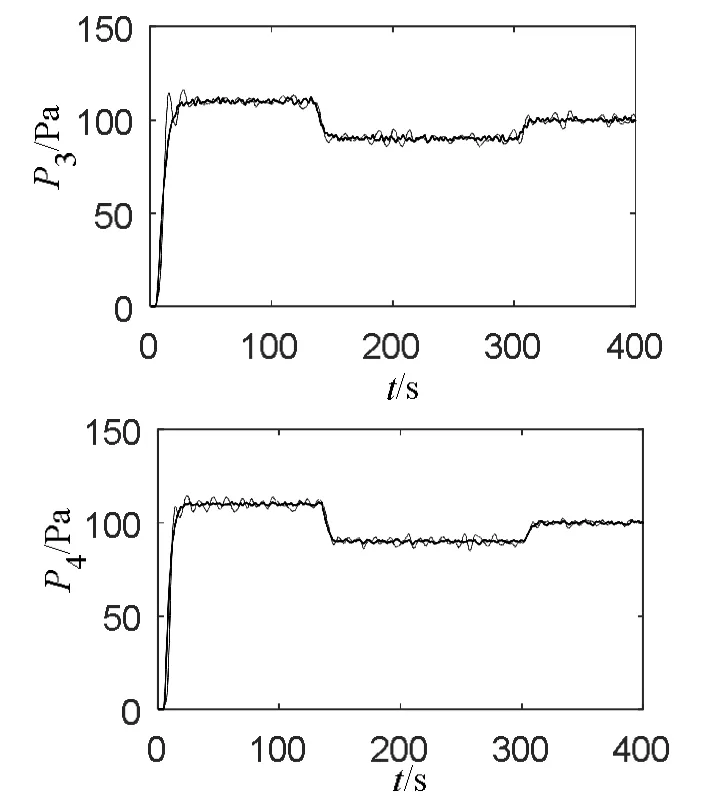
图6 随机扰动下的多模型与单模型预测控制输出对比曲线

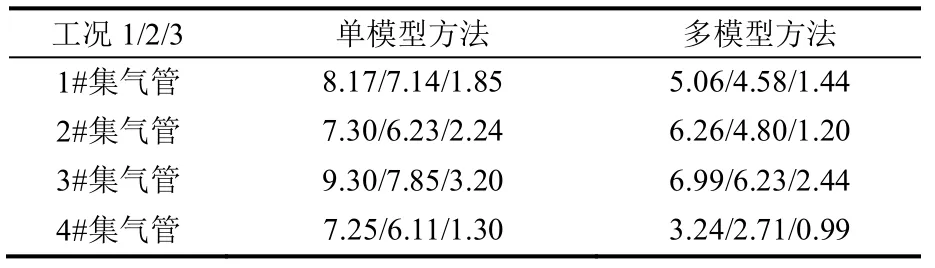
表2 随机扰动下两种控制策略下IAE 指标对比

由表2 数据可以看出，加入随机扰动后，当集气管压力受到随机扰动影响时，在本文的多模型预测控制方法在3 种工况下，比单模型预测控制情况下的控制精度较高、误差小，系统性能品质更好。

4 结论

（1）建模型动态特性与实际对象相符：焦炉产出煤气压力变化对对应集气管压力的影响最为显著；距离压力突变集气管越近的集气管，受到的耦合影响越强烈；同一组集气管之间耦合干扰更强烈。该模型建立合理，为控制器的设计提供给了方便。

（2）将此多模型预测方法与单模型预测控制情况下的控制效果进行仿真对比，在所有3 种工况中，本文方法控制精度高、误差小，控制品质更好。

（3）目前，焦炉生产集气管压力控制研究，均是针对结焦初期生产工况，没有考虑落煤、结焦末期等特殊工况下了建模与控制。本文针对3 种不同工况进行建模研究，并设计了焦炉集气管多模型切换策略，为焦炉集气管压力提供一种新的控制方案。