基于双因素学习曲线的建筑业技术学习率测算

（青岛理工大学 管理工程学院，山东 青岛 266000）

建筑业作为国民经济的重要产业部门，在国民经济中占的比例越来越高。在全球化日益加剧、经济快速发展的进程中，建筑业企业面临的环境更加复杂和多元化，仅仅依靠传统的人力、资源的投入已经不能满足建筑业在经济潮流中持续发展的需求，建筑业企业必须通过持续高效率的技术学习获取先进的技术，提高施工效率来适应快速变化的环境。而从行业角度对建筑业技术学习率进行估计，有利于相关管理者对建筑业长期技术学习路径的制定和发展方向的规划，有利于整个行业的技术分析和技术调整，对技术改革的时机做出正确的判断，从而保持建筑业高效的技术学习和持续发展。而如何对建筑业的技术学习率进行测定是一切技术学习活动的基础和前提。目前，国内外相关学者对于行业技术学习率的研究并不多，大多是对某种特定技术的技术学习率进行测算和分析。Arrow[1]首先提出了经验中学习的概念，应用单因素学习曲线对“干中学”技术学习率进行了测定；随后的一些学者如Murat 等[2]、Robert[3]采用非线性模型对不同产业的“干中学”学习率进行了测度；随着研究的深入，相关学者发现“研究中学”也会提高技术学习率。Miketa 等[4]、Jamasb[5]、Patrik 等[6]、Kristina等[7]、牛衍亮等[8]、管仕平等[9]、黄绍伦[10]、王树斌等[11]、迟春洁等[12]、Zhou 等[13]通过双因素学习曲线模型对不同产业或技术的技术学习率进行了测定，综合分析了从经验中学习和从研究中学习的学习率。

可以看出，现阶段对于技术学习率的研究主要应用单因素学习曲线和双因素学习曲线2 种方法。单因素学习曲线仅考虑“干中学”，也就是经验对于技术学习的影响，无法分析研究开发在技术学习中的作用，而双因素学习曲线考虑“干中学”和“研中学”，也就是考虑从经验学习和从研究开发中学习对技术学习率的影响，能够对技术学习率进行全面的测度。因此，本文建立了建筑业双因素学习曲线模型，赋予双因素学习曲线模型各变量新的含义，通过建立的建筑业学习曲线模型对我国建筑业技术学习率进行测算，最后基于测算的技术学习率对我国建筑业技术未来的发展提出一定的建议。

1 双因素建筑业学习曲线模型的构建

对于建筑业的技术学习，现阶段未有明确的定义，本文结合技术学习的概念和建筑业特点，给出了建筑业技术学习的概念：建筑业技术学习指的是随着建筑业技术的广泛使用和研发资金的不断投入而引起的技术改进的现象。

建筑业双因素学习曲线模型认为促使建筑业技术进步的因素有2 个：经验的积累和知识的积累。相对应的，建筑业技术学习率分为“干中学”学习率和“研中学”学习率，用于衡量2 个因素对建筑业技术进步贡献率的大小，技术学习率越大，表示技术学习效果越明显。

1.1 传统的双因素学习曲线模型

双因素学习曲线模型描述的是在累计产量和累计研发投入的作用下，单位成本的变化情况，其含义是刻画累计经验和研发投入对于技术进步的影响大小，表现形式为：

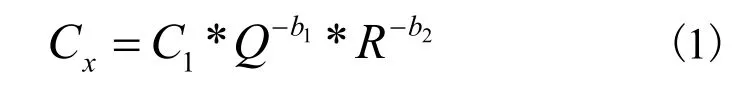
式中：Cx代表在x时刻的单位成本；C1表示研究期间内，生产第1 件产品时的成本；Q表示累计产量；R表示累计研发投入量；b1、b2分别表示干中学、研究中学的学习指数。

根据学习指数可以得出“干中学”和“研中学”的技术学习率分别为：，[14]。

1.2 变量的选取和定义

1.2.1 自变量的选取和定义

本文的自变量选取的是影响建筑业技术进步的2 个因素：中国建筑业累计施工面积和中国建筑业累计R&D 经费内部支出。建筑人员在工作中进行技术学习，随着累计施工面积的增多，工作人员技术逐渐熟练，效率逐渐增高，而以往技术的掌握又会促进新技术的产生。累计施工面积指的是从第一年开始到第N年的施工面积之和。而考虑到研发投入的滞后性和知识存在折旧的情况，累计R&D经费内部支出指的是从第一年开始到第N年的知识累计存量。

1.2.2 因变量的选取和定义

本文的因变量选取的是中国建筑业单位施工面积对应的成本(单位面积成本)，根据赵明[15]的研究，本文选取建筑业固定资产投资作为建筑业物力投入，建筑业职工工资作为人力投入，营业成本与职工工资和固定资产折旧作为建筑业财力投入，三者之和(固定资产投资+营业成本-固定资产折旧)作为建筑业总成本。每年的建筑业成本除以当年建筑业总施工面积构成单位面积成本。

1.3 不定参数的选择和定义

本文使用情景分析法，选择以下3 个不定参数。

单位成本下降的预计极小值。在累计施工面积和研发投入的作用下，建筑业技术会不断改善，建筑成本也会逐渐降低，但不会一直降低，单位成本的降低会逐渐趋向平缓。因此将估计的单位面积成本下降的极小值作为一个不定参数，可以更合理地对技术学习率进行测算。

研发滞后期数。研发滞后期数是指研发经费发挥作用，能够促进技术进步的时间与经费投入时间的时间差，一般以年为单位。对于研发投入之所以要考虑到滞后期的因素，是因为某个新技术的产生是需要一个时间过程的，少则数月，多则数年，而新技术产生以后也要经过试验等过程才能应用于具体的施工过程中。因此当年的研发经费投入并不是立即能促进技术的改善，而是会在今后的几年才会促进技术的进步。

知识存量折旧率。知识存量折旧率指的是由于新技术的出现等原因导致的以前旧的技术在每一年的淘汰率。因为知识存量也是一种无形资产，所以其必定面临折旧。随着建筑业技术的不断发展，新的技术不断出现，旧的技术不断被淘汰，只有某些有价值的技术被保留下来，因此将知识存量的折旧率作为一个不定参数，可以更全面地对“研中学”技术学习率进行测算。

1.4 模型构建

对于传统双因素模型进行修正，一方面，由于熟能生巧，随着产量增多，工作人员通过学习，工作效率提高，进而引起成本降低，这种由于产量增多而引起成本下降的现象称为“干中学”；另一方面，研发人员在研究初期困难大，随着研究深入，在不断试验中学习，在后期对于前期成果的改正工作较易，这种由于研发投入引起成本下降的现象称为“研中学”。因此在基于产量和研发2 个学习因素对于成本的影响，建立我国建筑业学习曲线模型：

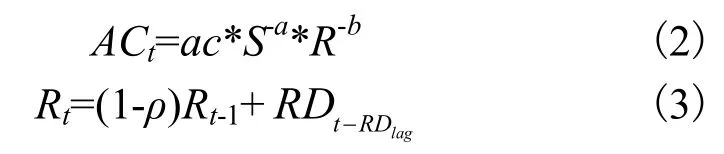
其中，ACt为第t年的建筑业单位面积成本；ac为基期单位面积成本(ac＞0)；a为“干中学”学习指数（0＜a＜1)表示累计施工面积对于成本下降的贡献率；b为“研中学”学习指数(0＜b＜1)，表示研发投入对于成本降低的贡献率；S为累计施工面积；R为累计R&D经费内部支出，式(2)“干中学”和“研中学”学习率计算公式分别为：LR=1-2-a，RR=1-2-b。可以看出，学习指数a、b越大，学习率越大，此时学习效应越明显。Rt为t时期的建筑业技术知识存量，ρ（0＜ρ＜1）是知识存量的折旧率，Rt-1指的是t时期上一年的知识存量，指的是在研发投入存在滞后期的情况下，研发经费投入对知识存量的贡献值，RDlag为研发经费投入和对知识存量产生影响之间的滞后时间。式(3)为累计知识存量的计算公式，此公式的设立同时考虑研发滞后期数和知识存量折旧率对于当年知识存量的影响，使测算结果更合理准确。

对式(2)求自然对数得：

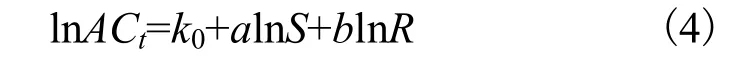
再考虑到单位面积成本的下降存在最小值，则建筑业学习曲线模型为：

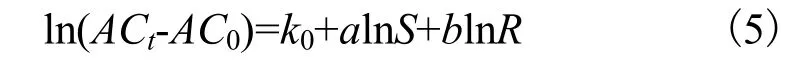
由式(5)可知，单位面积成本的预计最小值会对因变量产生影响，而由式(3)可知，由于考虑到研发投资滞后期和知识存量折旧率的影响，ρ和RDlag会影响每年知识存量的变化，从而对技术学习率的测算结果产生影响。本文结合情景分析方法，在相关学者的研究基础上，找出最优情景组合，对我国建筑业的技术学习情况做出综合评价。

3 基于建筑业双因素学习曲线模型的情景分析

3.1 数据收集与处理

本文收集了2002—2018 年我国建筑业相关数据，如表1 所示。

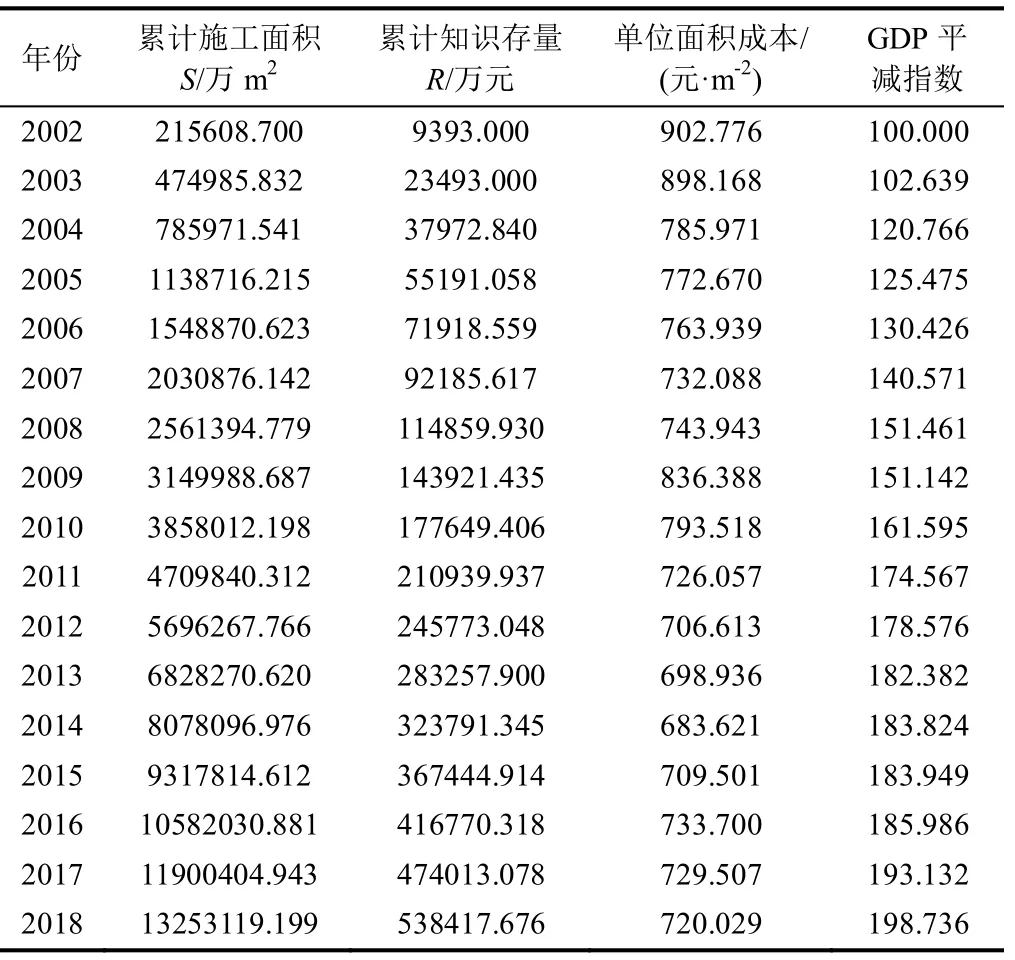
表1 2002—2018 年中国建筑业相关数据

数据来源及说明：由于我国建筑业R&D 经费内部支出从2002 年开始统计，考虑到数据的可获得性，本文选取的时间跨度为2002—2018，共17年。建筑业施工面积来源于《中国建筑业统计年鉴》，累计施工面积指从第一年开始到某时期内的施工面积之和；建筑业R&D 经费内部支出来源于《中国科技统计年鉴》。R&D 经费内部支出经过技术研发，会变成企业的知识存量，而累计研发投入指的是从第一年开始到某时期内的知识存量之和。单位面积成本=建筑业当年总成本/当年施工面积。用GDP 平减指数对单位面积成本进行处理，以消除通货膨胀的影响。

3.2 情景构建

孙凤娥等[16]在对我国以及各地区R&D 资本存量的研究中，对我国以及各个地区的R&D 折旧率均采用20.6%，因此本文假设建筑业知识存量折旧率ρ可能有下列3 种情况：15%、20%和25%。假定我国建筑业研发投入的滞后期分别为1 年、2 年和3 年。2018 年，我国建筑业单位面积成本为720.029 元/m2，因此本文假定建筑业单位面积成本的极小值有以下3 种情景，即650、600、550 元。

以上不同参数的不同取值构成了30 种不同的情景组合(AC0，ρ，RDlag)，在不同的情景组合下，本文将表1 中的数据取其对数形式，为回归分析做准备。

4 回归分析和技术学习率的测算

4.1 回归分析

基于不同的情景组合，首先使用公式(4)计算每种情景下的累计知识存量，然后使用软件SPSS23.0 对公式(6)进行回归分析，根据回归分析的检验值选出最优情景组合。最后计算出该最优情景下的技术学习率。对30 组不同的情景(AC0，ρ，RDlag)做回归分析，回归分析结果如表2 所示。

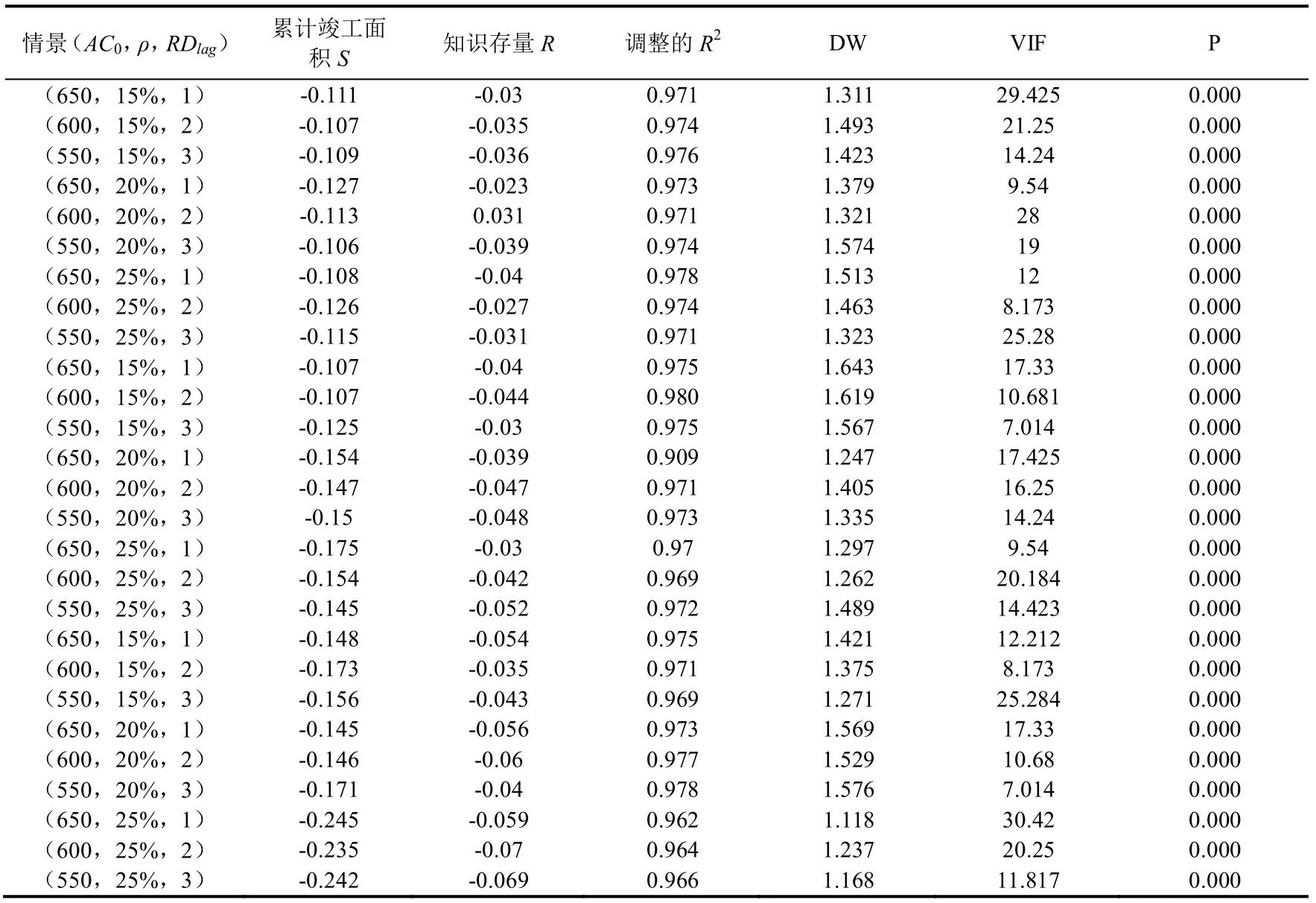
表2 各情景回归分析结果

由表2 可以看出，“干中学”和“研中学”系数均为负，说明累计施工面积和累计研发投资都和单位成本是负相关的，也就是说，和技术的进步是正相关的。在(50，20%，3)的组合下，除了统计量VIF，其他统计量都为最优，因此该情景组合为最优情景组合，即建筑业单位面积成本最小值为550元，知识折旧率为20%，研发投资滞后期为3 年。

4.2 技术学习率的计算与分析

在最优情景(550，20%，3)下，“干中学”技术学习率1-2-a=12.58%，说明累计施工面积每增加1 倍对于建筑业技术的贡献率为12.58%，单位成本下降的百分比为12.58%。“研中学”技术学习率1-2-b=2.8%，说明知识存量每增加1 倍对建筑业技术进步的贡献率为2.8%。

“干中学”的技术学习率明显大于“研中学”技术学习率，说明在建筑业的发展过程中，在经验中学习产生的学习效应比研发投入产生的学习效应更能促进技术的进步。但是未来随着建筑业的发展，建筑业的知识存量会不断累积，在无论企业还是国家都越来越追求高技术的将来，难以保证“研中学”对技术进步的影响不会超过“干中学”。

对于情景分析中的的不定参数，最优组合为(550，20%，3)，预计建筑业单位面积成本会下降到550 元/m2，说明现阶段建筑业技术还有待改善，施工、管理等各方面效率还有待提高。

知识折旧率为20%，与全国知识折旧率仅差0.6%，说明建筑业的技术更新进步处于全国平均水平，企业在研发过程中存在着知识折旧率，即今年会淘汰去年落后的20%的技术和经验，以不断融入新技术，形成新的知识存量。

研发投资的滞后时间为3 年，说明当前的研发资金投入要3 年以后才能形成新的技术，促进行业的发展。说明对于整个建筑行业而言，新技术的产生不易，也说明我国建筑业追求研发的质量。

5 结论及建议

5.1 结论

构造了建筑业双因素学习曲线模型，选取单位面积成本作为因变量，综合评价“干中学”和“研中学”对建筑业技术进步的贡献，通过学习曲线理论与情景分析的方法，对中国建筑业业的技术学习率进行了估计，得出“干中学”技术学习率为12.58%，“研中学”技术学习率为2.80%。即经验学习对技术进步的贡献率为12.58%，研究开发对于建筑业技术进步的贡献率为2.80%；经验中学习和研发中学习都对技术变革有重要影响；估算的研发滞后时间为3 年，知识折旧率为20%，单位成本下降的预计最小值为550 元。本文综合评价了我国建筑业技术学习状况，有利于相关决策者合理制定建筑业技术的未来发展路径。

5.2 建议

“干中学”在技术学习中发挥着最为突出的作用，“干中学”技术学习率明显超过“研中学”技术学习率，从侧面说明了我国建筑业仍属于劳动密集型产业的事实。对“干中学”技术学习率影响最大的是建筑从业人员的工作能力。因此企业在考虑技术改善与发展方向上，要注重企业员工的内部培训，提高从业人员的工作能力，因而提高工作的效率和质量，这样就可以促进企业技术进步，给企业带来更多的发展优势。

“研中学”对建筑业技术进步的贡献不如“干中学”显著，但是“研中学”对降低成本也十分重要，可以大胆预测，甚至随着科技的进步，在未来某一时刻，“研中学”对于企业技术发展的影响会超过“干中学”的影响。研发投资可以在一定程度上促进技术进步，然而现阶段我国建筑业技术还比较落后，科技人才比较匮乏，因此相关企业及政府应注重建筑业研发人员的培养和引进，以及生产先进设备助力建筑业发展，使建筑业技术有一个质的飞跃。