区间自适应遗传算法优化BP 神经网络权值阈值研究

（辽宁工业大学 管理学院，辽宁 锦州 121001）

遗传算法和神经网络是智能算法中两个重要方法。BP（Back-Propagation algorithm）神经网络本质上是基于梯度下降的一种迭代学习算法，其误差曲面是非常复杂的多元曲面，存在许多局部极小解，当梯度为0 时，BP 算法则无法辨别极小点性质，使训练难以收敛到指定误差；若在误差曲面平坦区，则调整时间长，影响收敛速度[1]。为了克服这些缺陷，学者提出了许多改进措施，如附加动量项、自适应学习率，与现代优化方法结合等。而建立在遗传学基础上的遗传算法（genetic algorithms，GA）主要特点是对目标函数无限制，广泛用于人工神经网络训练与优化问题[2-3]。

如何使遗传算法和BP 算法有机结合，许多学者做了大量研究。一般用遗传算法优化BP 神经网络结构和初始权值阈值[4-5]。但遗传算法求解优化问题时，只能求得给定区间内的优化值[6]。而神经网络权值和阈值所在区间一般无法预知，故本文采用能够动态调整权值和阈值所在区间的自适应遗传算法（IAGA），彻底取代BP 算法反向调整权值阈值的过程，达到自适应调整权值阈值的目的，从而将BP 算法和IAGA 有机结合起来，充分发挥各自优势，有效克服BP 算法学习过程中易陷入局部极小值、振荡等缺陷。

1 BP 算法及IAGA 算法

1.1 BP 算法原理

三层BP 算法其结构如图1 所示。

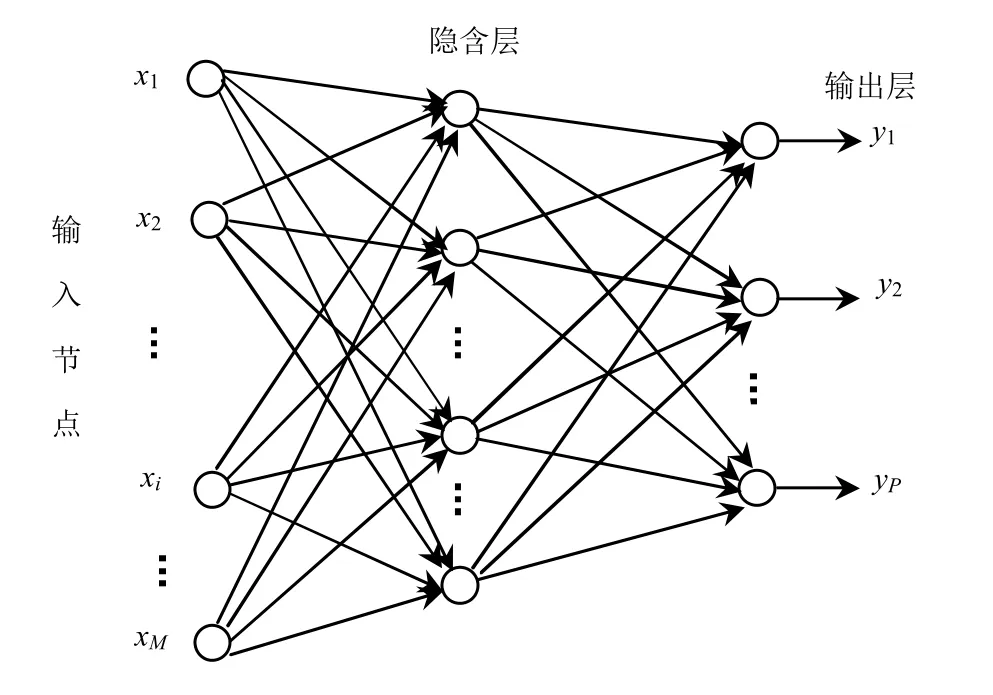
图1 BP 神经网络的结构

X=[X1,X2,…,Xk,…,XN]为N个训练样本集，Xk=[Xk1,Xk2,…,XkM]T为任一训练样本，(k=1,2,…,N)，Yk=[yk1,yk2,…,ykP]T实际输出为，dk=[dk1,dk2,…,dkP]T为期望输出。神经元激励函数均使用Sigmoid 函数：

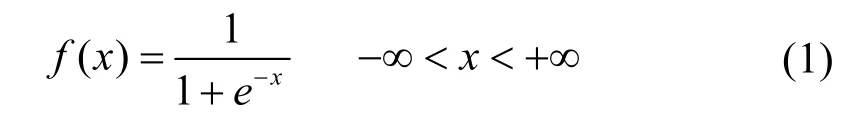
经神经网络正向传播后工作信号的实际输出为：

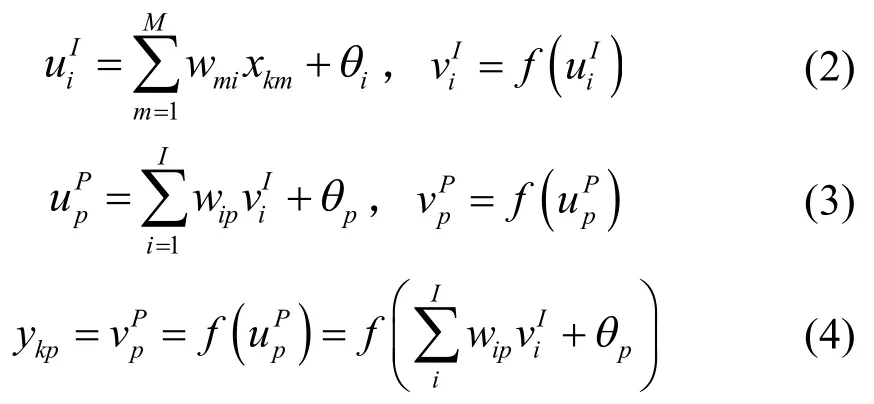
式中：i=1,2,…,I，p=1,2,…,P

设n为迭代次数，权值、阈值和网络实际输出是n的函数。则输出层第p个神经元误差信号为：

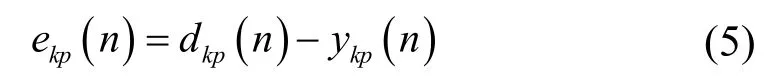
神经元p的误差能量定义为，则输出层所有神经元的误差能量总和为E(n)：

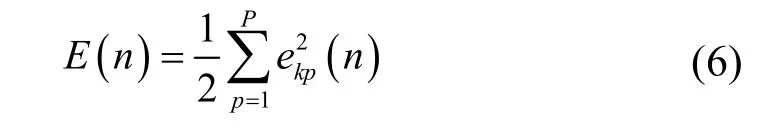
在误差信号的反向传播过程中，BP 算法是通过调整权空间中的梯度使E(n)值下降的，详细推导过程见文献[7]。

1.2 IAGA 算法描述

为了能更好的说明IAGA 自适应移动搜索区间的过程，以某一权值在初始区间[U1,U2]中的调整过程为例，且U1＞U2，U2点的目标函数值优于U1点。随机产生pop个初始种群，设所有神经元的误差能量总和达到指定较小精度要求时所对应的权值为ω*，且ω*不在[U1,U2]内，ω*＞U2。经过几次选择、交叉和变异遗传操作后种群中目标函数值最小的个体逐渐向U1点趋近，这时可取

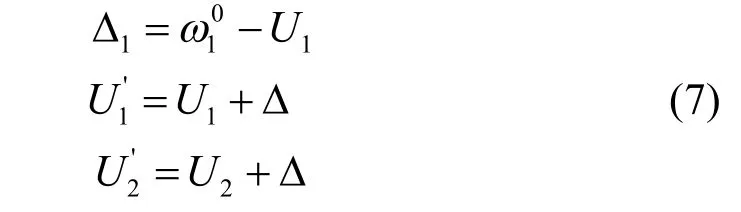
2 IAGA 优化BP 算法

2.1 IAGA 优化BP 权值阈值的思想

神经网络最优解所对应权值和阈值的区间范围一般很难预知，而遗传算法求解优化问题时，若最优解不在给定的取值范围内，只能求得一个指定区间内的较优解，有可能求不到真正使误差能量总和达到指定精度要求的较优解，使神经网络的拟合效果下降，为此本文将区间自适应遗传算法用于神经网络权值阈值的调整，即用IAGA 的优化功能，取代误差信号反向传播逐层修改权值和阈值的过程。IAGA 优化BP 算法的数学模型为：

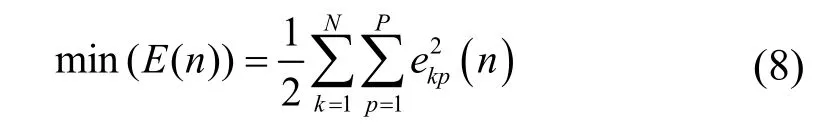
2.2 IAGA 优化BP 权值和阈值算法描述

步骤1：对训练样本进行预处理。

为避免出现奇异样本数据所引起训练时间增加和无法收敛等问题，将训练样本数据进行归一化处理，使量纲数据变为无量纲纯量。

步骤2：变量的初始化。

输入：种群规模pop，最大迭代次数T，交叉概率pc，变异概率pm，权值与阈值的初始区间。

步骤3：计算码长，随机产生初始种群。

步骤4：设置迭代次数t=0。

步骤5：形成父代种群。

步骤6：解码。

步骤7：保留m个适应度高精英个体。

步骤8：选择。

步骤9：交叉。采用单点交叉方式。

步骤10：变异。

步骤11：保留优秀个体[8]。

步骤12：判断是否满足更新区间条件，不满足，则执行步骤13，满足则移动搜索区间。

步骤13：将交叉产生的个体，按自适应变异方式进行变异。

步骤14：精英替代变异后适应度值低的个体。

步骤15：形成新一代种群，遗传进化一代完成，即t=t+1；

步骤16：判断训练误差结束条件，满足则终止遗传运算，不满足要求，则转到步骤5。

步骤17：将计算得到的权值和阈值代入工作信号正向传播的输出公式(4)，并计算神经网络的实际输出。

步骤18：反归一化处理。为了与原始数据拟合，需将神经网络的输出数据反归一化处理。

步骤19：与试验数据拟合。

3 仿真结果与分析

3.1 试验数据与预处理

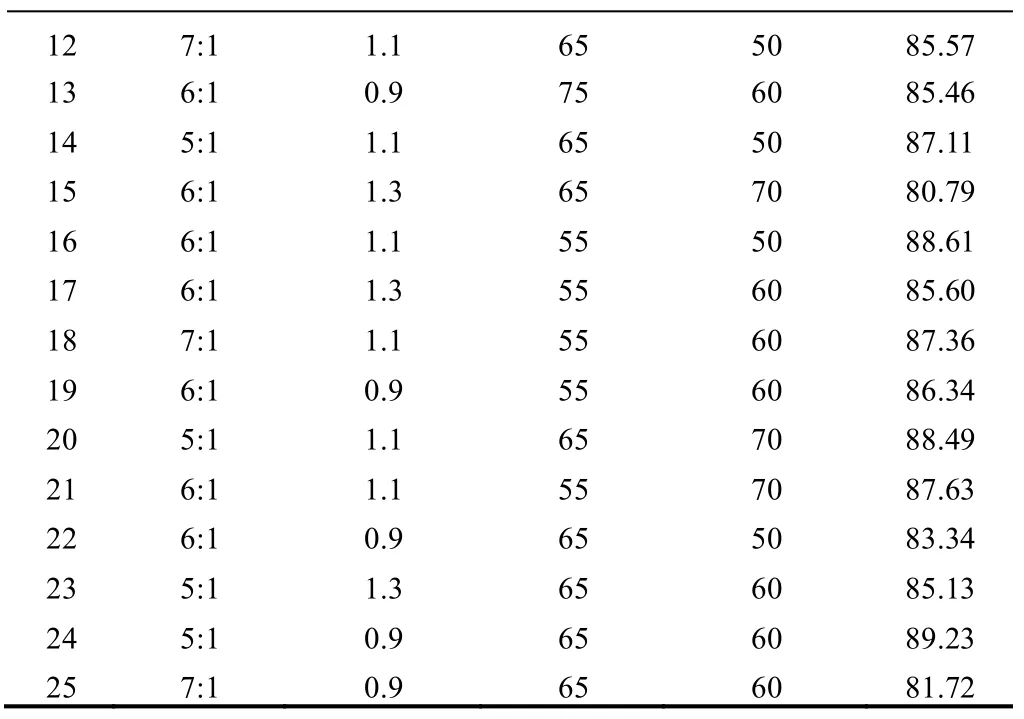
用曹秀丽等[9]所做的大豆油甲酯合成工艺试验数据为训练样本，验证区间自适应遗传算法优化神经网络权值阈值，试验训练数据如表1 所示。因Sigmoid 函数在接近0 或1 时，基本达到饱和状态，增加变慢，故将试验数据归一化处理到区间[0.1,0.8]之间，加快网络的收敛速度。

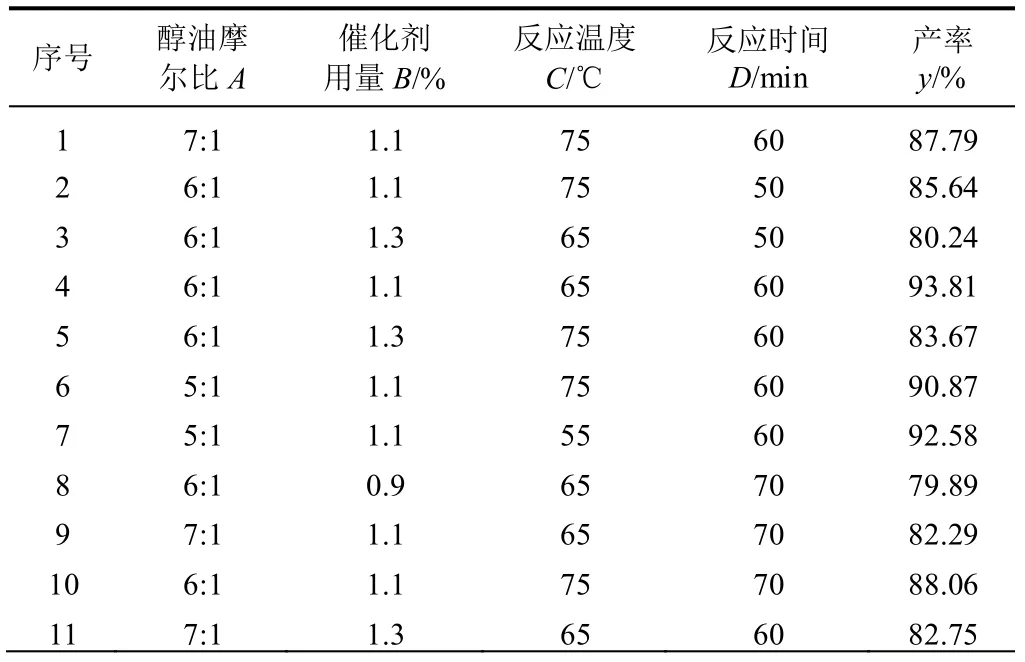
表1 试验训练样本

3.2 BP 神经网络的训练

网络结构为4-7-1。权值和阈值初始区间取值为[-10,10]，种群规模80，编码精度为1.00e-4。当遗传操作代数count=1 000 时，进行区间移动。交叉概率pc=0.95，变异概率pm=0.05，精英个体数4。用MATLAB R2016b 编程完成上述思想，当输出误差达到2.58×10-8时，算法结束，此时得到的权值阈值结果为：

将训练好的权值和阈值代入BP神经网络工作信号正向传播过程的计算公式，即式(4)，可得网络的实际输出，并实际输出反归一化处理后得到如表2所示数据。

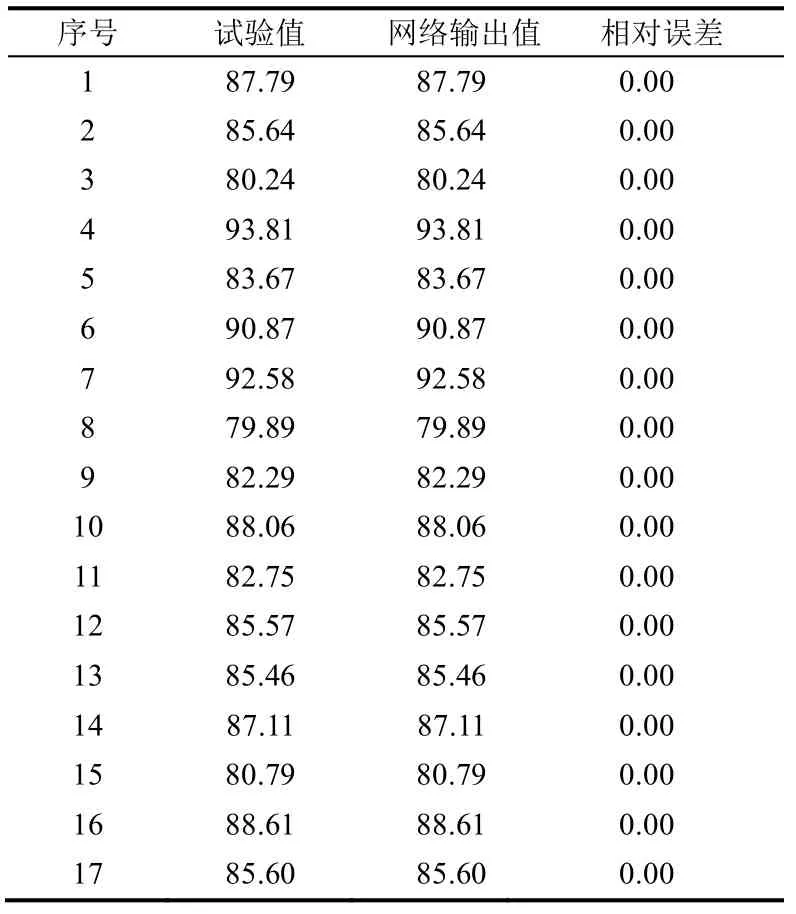
表2 网络输出值与实验值拟合精度情况 %

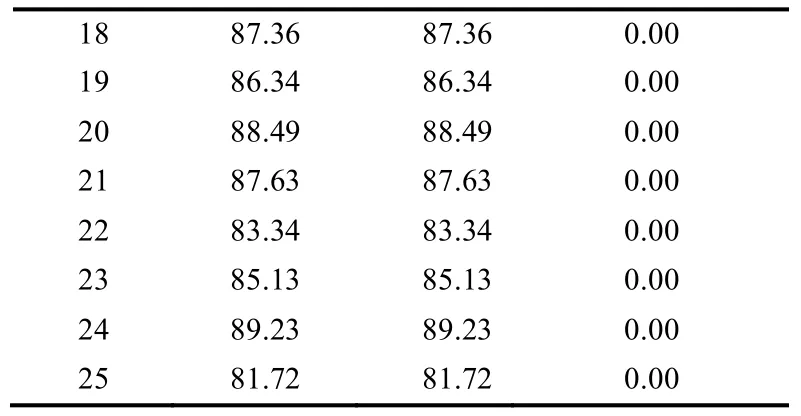
从表2 可知，用IAGA 优化方法替代梯度下降法来调整权值和阈值，可使BP 神经网络的输出数据与实验数据完全拟合，说明是一种有效的权值阈值调整方法。

4 结论

用IAGA 彻底取BP 神经网络反向调整权值和阈值的方法，可以两种智能优化方法各自的优点有机地结合起来。IAGA 具有优化BP 神经网络的能力，解决了BP 算法的困境。计算结果表明，该方法可使训练误差的目标值达到很高的学习精度。在大豆油甲酯合成工艺问题中，误差可以达到2.58×10-8，平均相对误差为0%，证明了该方法是一种可靠有效的优化方法。