隔震结构方程的一种压缩解法

田志昌， 孙欣欣， 李 娟， 李 革， 杨志军， 陈 明

(内蒙古科技大学 土木工程学院，包头 014010)

1 引 言

基础隔震[1]能够有效提高结构的抗震性能，为了达到理想减震效果，一般隔震设计中支座滑动时的刚度非常小。利用有限元软件解决大规模的代数方程计算问题，方程能否得到可靠的解取决于刚度矩阵的正定性条件。在基础固定结构体系中，通常采用逐步积分，如Newmark法，基本不存在问题。但在基础隔震的情况下，上部结构的刚度矩阵在遇到隔震支座较小的刚度时，总刚度矩阵正定性条件变差，会出现病态方程[1-4]。病态方程的解常偏离真值[2]。根据文献[2]，解决这个问题的办法有两种，一种是保证刚度矩阵中的元素差异不要太大，这显然违背了物理原理；第二种是降低矩阵规模，减缓病态。

针对此现象，本文提出利用上部结构本身的振型叠加来压缩未知量，进而减小刚度矩阵的规模。将振型叠加后的方程与隔震器参数联合形成新的不对称混合方程组。无论上部结构有多大规模，未知数目有多少，都能通过振型叠加法压缩至几十个未知数之内。根据隔震结构的特点，隔振器增加不到10个未知参数即够用。一个1万自由度的中型结构，可以用15个振型和3个支座刚体位移描述。可见压缩量达10000:18。一个18阶的方程即使系数不均匀，但计算收敛也是可靠的；而1万阶的大型刚度矩阵中，若出现非常小的刚度就会引起方程解相对误差很大的病态问题。

2 基础隔震结构体系运动方程求解

2.1 计算模型

以底部带有基础隔震器的n层框架结构为计算模型，如图1所示。

根据结构体系的模型，可写出该模型的质量矩阵、刚度矩阵和阻尼矩阵，阻尼采用Rayleigh阻尼，即C=αM+βK。无隔震器结构的总未知量为n，加入隔震器支座后增加了一个未知量，即结构的质量矩阵和刚度矩阵等的阶数增加为n+1。对隔震与上部主结构体系进行分块，矩阵可表示为

[M]n+1×n+1=m1⋱mnm0=Mn×n00m0

(1)

[K]n+1×n+1=k11︙⋱-k0knn︙…-k0…k0=Kn×nKn×1K-1×nk0

(2)

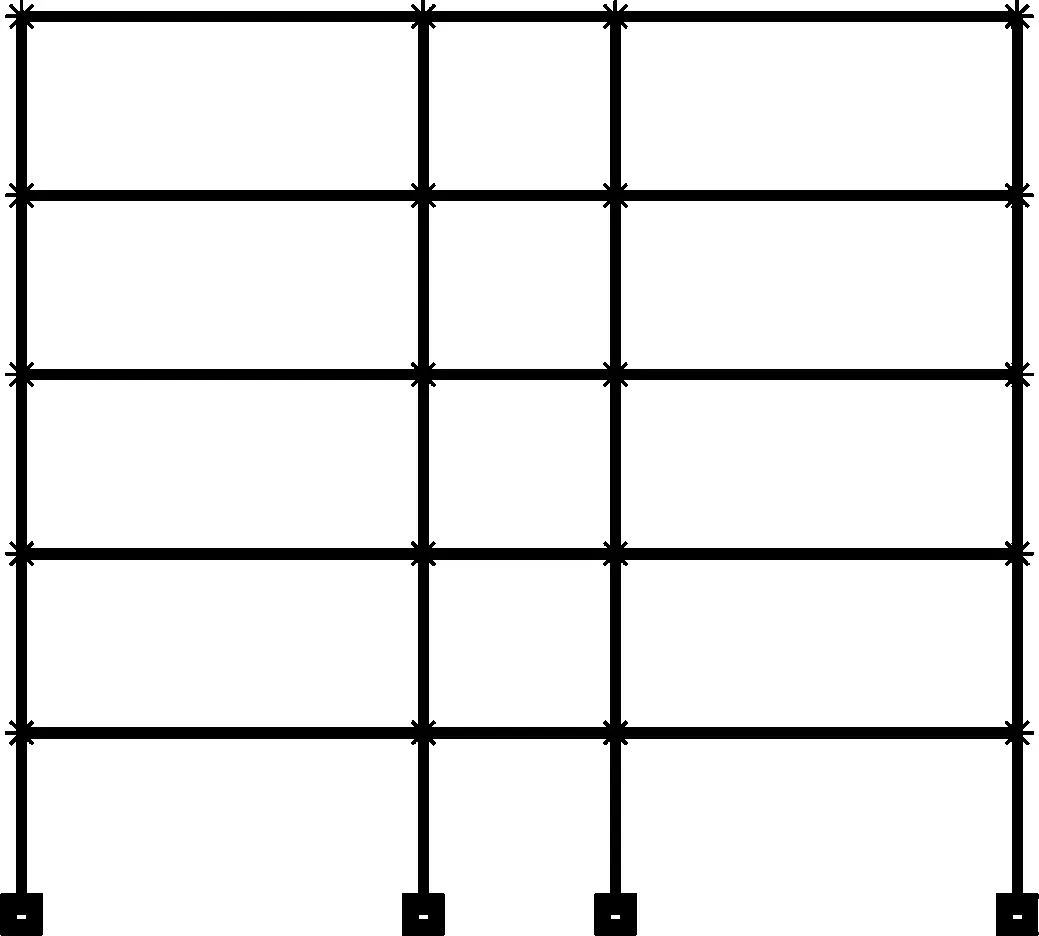
图1 n层框架结构模型

[C]n+1×n+1=c11︙⋱-c0cnn︙…-c0…c0=Cn×nCn×1C1×nc0

(3)

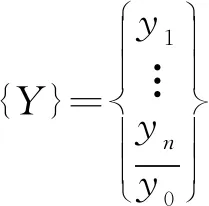
(4)

(5)

式中Mn × n,Cn × n,Kn × n和yn分别为上部主体结构的质量、阻尼、刚度和位移，m0，c0，k0和y0分别为基础隔震器质量、阻尼、刚度和位移，Yn × 1为结构相对基础的位移。

综上所述，一个n+1自由度的隔震结构模型在地震作用下的运动方程为

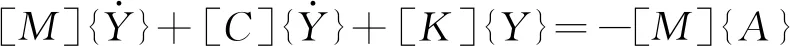
(6)

2.2 压缩未知数

方程按照上部体与基础隔器分块表示为

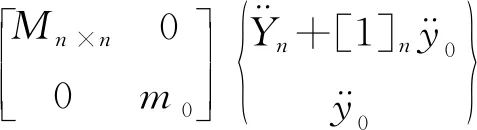
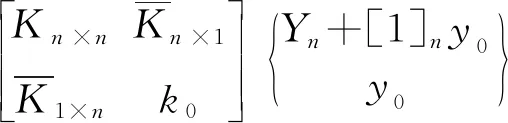
(7)

将式(7)的质量及刚度与主体系矩阵分离，可以表示为

(8)

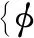
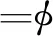
(9)

(10)

结构处于弹性阶段的振型矩阵，即

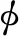
由模态的正交性[4]可知，在i≠j时，有

(11)

则式(10)可写成

(12)

将式(12)合并成统一方程得

(13)

式(13)即为结构在m个模态广义坐标下添加隔震器的运动方程，其共有m+1个方程(m为结构的模态数量)。与用振型叠加法压缩未知数的式(7)相比，方程数量明显减少，刚度矩阵规模也减小，此时组合方程包含已压缩未知量的上部结构方程和基础隔震器结构方程。

3 算法的正确性验证

3.1 计算模型基本参数

该结构为四层框架结构教学楼，层高均为3.9 m，房屋总高度为15.6 m，场地类别为二类，抗震设防类别为乙类，设防烈度为8度，柱截面尺寸为500 mm×500 mm，梁截面尺寸均为300 mm×600 mm，楼板厚度为120 mm，采用C30混凝土，结构标准层平面如图2所示。

图2 结构标准层平面

3.2 地震波数据

本文选用典型的Ⅱ类场地的El Centre地震记录，取0 s～30 s的地震波进行研究，并将地震波划分为1500步，每0.02 s为一个步长[9]。

3.3 分析结果对比

如图3所示，对框架结构进行静力分析时，在相同结点位移处的位移，用正常解法和压缩解法分别求解方程，比较两种解法结果，一次求解两种算法结果基本一致，如图3(a)所示，水平位移误差在 0.5% 以下，如图3(b)所示；在转角处的位移值基本一致，如图3(c)所示，算法误差比值在1%左右，如图3(d)所示。

如图4所示，NewMark时程计算压缩方法在 30 s 内的方程求解是收敛的；如图5所示，在同等条件下，正常解法和压缩解法在0.38 s以前的位移响应保持同步，但0.4 s以后正常解法的位移开始出现异常，后续累积发散。

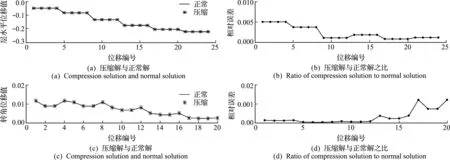
图3 压缩解法和正常解法结果比较

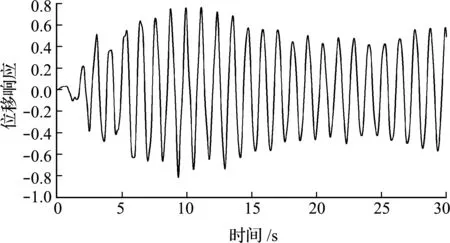
图4 压缩解法

图5 正常解与压缩解比较

4 结 论

本文提出了适用于大型结构和高层建筑隔震体系的压缩解法，通过一个框架算例，比较了正常解法和压缩解法的计算结果，得出如下结论。

(1) 两种算法在相同结点处的若干次解的位移值基本吻合，尤其是在地震波横波作用时，误差比值在0.5%以下，证实了压缩解法在框架结构静力分析中的准确性与有效性。

(2) 在逐步积分法中，正常解法累积误差可导致结果发散，而压缩解法则不会出现发散。