Laplace变换法及其在粘弹性波中传播的应用

李 想， 陈国平， 胡文军， 谢蒙优

(1.西南科技大学 土木工程与建筑学院,绵阳 621010；2.中国工程物理研究院 总体工程研究所,绵阳 621900)

1 引 言

近年来，随着科学技术的发展，泡沫和橡胶等聚合物由于其质量轻和阻尼高等特点广泛地应用在国防科技和航空航天等领域，作为缓冲、降噪及减排材料。该类材料在使用过程中常涉及冲击、碰撞和爆炸等问题，因此获取材料的动态力学性能尤为重要，许多学者做过此方面研究[1,2]。测量材料动态力学性能最常用的实验方法有落锤实验、摆锤冲击实验和分离式霍普金森压杆实验(简称SHPB)。SHPB实验技术由于其原理简单、操作方便和设计巧妙等优点，已成为最经典的测量材料动态力学性能的实验技术。SHPB实验技术基于两个基本假设，即一维应力波假定和试件应力均匀假定[3]。传统的SHPB装置为了确保压杆在实验过程中始终保持弹性状态，多采用高强度钢制作，波阻抗较高，而橡胶和泡沫等粘弹性材料波阻抗较低，使用传统的SHPB实验装置研究粘弹性材料，会造成波阻抗严重不匹配，从而导致入射波和反射波较为接近，透射波信号微弱，无法使用二波法或三波法确定应力和应变。王礼立等[4]首先提出了使用粘弹性压杆的SHPB实验技术，从而解决了波阻抗不匹配问题。

当使用粘弹性压杆来替换高强度钢杆时，若用应变片处测得的信号来代替压杆与试件接触端的信号，其结果会与真实值存在较大的误差。这是由于应力波在粘弹性杆中传播涉及到波的幅值衰减和波形弥散问题，所以必须对波形进行修正，修正波形需对应力波在粘弹性材料中的传播规律进行研究，才能确定压杆和试件接触端的动态响应情况。因此，研究粘弹性波传播问题十分必要。

本文对应力波传播分析方法进行了简要的综述，详细介绍了几种处理粘弹性波传播问题的分析方法，对比分析几种方法在各自应用上的优劣，重点介绍Laplace变换及其在粘弹性波中的应用。

2 粘弹性波传播分析方法

为分析无限圆杆上一维纵波传播问题，文献[5]给出了相速度和频率相关的频率方程，该方程只在无限弹性圆杆的情况下才有精确解。目前，对于应力波传播的分析方法多以该频率方程为基础进行研究，文献[6，7]对该方程纵波解进行了修正，文献[8]指出了纵波解在有限条件下的不精确性。

到目前为止，研究粘弹性波传播的几种方法都趋于成熟，分析粘弹性波传播正问题的方法主要有Laplace变换法、小波变换法、特征线法和传播系数法；分析粘弹性波传播的反问题研究方法主要有波传播实测信息的反分析法。

2.1 特征线有限差分法

特征线有限差分法是指对沿波前沿扰动的特征相容关系进行差分，结合Lagrange质点的粘弹性记忆效应，将求解波动方程组转化为用差分的方法求解相应特征线方程和相容方程的方法。文献[9，10]均采用特征线法研究SHPB实验中粘弹性试件的应力不均匀性，王礼立等[3,4]详细叙述了线性粘弹性杆中纵波的特征线解法。江伯涛[11]应用特征线法研究了橡胶内部应力波传播的粘弹性特性；赖华伟等[12]应用特征线法分析了线性粘弹性球面应力波问题；雷卫东等[13]研究了爆破荷载应力波在无限弹性介质中传播的特征线解。以Maxwell模型细长杆中线性粘弹性纵波传播为例说明特征线解法。

一维粘弹性试件中的波动控制方程组：

运动学方程

(1)

连续方程

(2)

Maxwell本构方程

(3)

将式(1～3)通过方向导数法处理得到x-t平面的三族特征线和相应的特征相容关系：

(4)

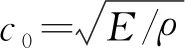
特征线有限差分法已经较为成熟，在工程应用中，其计算结果准确，接近理论解，十分便利高效，但其处理混凝土等大尺寸构件时，计算过程较为繁琐，耗时长，成本高，达不到预期效果。

2.2 传播系数法

传播系数法是建立在粘弹性波传播理论的Fourier谐波上的分析方法。传播系数法在粘弹性波的分析中研究较多，Bacon[14]提出了利用粘弹性杆进行SHPB实验和测量传播系数的实验方法；Butt等[15]对Bacon提出的方法进行了补充验证；Zhao等[16,17]将Pochammer-Chree推广到粘弹性圆柱研究中；刘孝敏等[18]在文献[14]的基础上，导出表征波衰减和弥散性质的纵波传播系数的修正公式；张方举等[19]采用波传播系数实验方法分析PC杆中的波传播过程，得到了PC杆中与波衰减和弥散相关的波传播系数；Aleyaasin等[20]用传播系数法重点讨论了材料性能和杆径对衰减和弥散系数的影响。

根据Bacon[14]对传播系数的定义，粘弹性杆轴向运动的一维方程(忽略横向惯性效应，应力波的波长比杆径大的时候)，横向惯性效应引起的几何效应可以忽略不计。

对式(1,2)进行傅里叶变换可得一维频域纵波波动方程为

(5)

线性粘弹性材料一维频域本构方程为

(6)

E*为材料的复杨氏模量，定义传播系数为

(7)

联立式(5～7)可得粘弹性杆轴向运动的一维方程

(8)

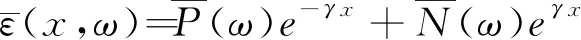
(9)

轴向粒子速度v和法向力F为

(10)

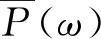
2.3 波传播实测信息的反分析法

反分析法是指通过测量距冲击点一定距离处某些部位的响应,如位移、速度、加速度或应变,来确定冲击点处的冲击力。为了解决由于测量条件限制而产生的冲击力难于测量的问题，近年来反分析法得到发展。Inoue等[21]对冲击力间接测量的反分析方法进行了综述；卢静涵等[22]将反分析法应用到对压力管道耐撞性侧向冲击实验中冲击力的校核,给出了该冲击系统的传递函数h(t)，在实验测量值的基础上,得出了较为精确的冲击力时程曲线,从而验证了该方法的实用性；王志华等[23]利用反分析法中的反卷积技术给出SHPB中波导杆的传递函数,完善了该实验装置的数据处理系统，并利用传递函数h(t)对泡沫铝动态特性实验中测得的波形进行了校正。

在结构上给定点处的冲击力和相应之间的关系可以通过线性卷积公式给出：

(t>0) (11)

f(t)=h(t)=e(t)=0

(t<0) (12)

式中e(t)是结构响应，f(t)是冲击力，h(t)是传递函数。记F(ω)，H(ω)和E(ω)分别为f(t)，h(t)和e(t)的Laplace变换。对式(11)进行Laplace变换可得

(13)

由式(11)可得

H(ω)=E(ω)/F(ω)

(14)

由此可求出H(ω)，并将其做Laplace反变换可得

(15)

通过式(15)可求出传递函数h(t),式中S=Re(ω)。在传递函数h(t)已知的情况下，若已知冲击的结构响应e(t),就可根据反卷积技术求得冲击点的冲击力时程f(t)。

在实际应用中，利用反分析法求解冲击力f(t)时，求得传递系数h(t)最为关键，不同的系统对应不同的传递系数h(t)，现多使用计算机有限元仿真模型计算传递系数h(t)，建立与实际相符的模型较为困难，且计算结果存在一定误差。

2.4 小波变换分析法

小波变换是在Fourier变换的基础上发展而来，是对Fourier变换的补充和升华。Fourier变换处理非平稳信号最大的缺点是无法获知频域上的时间信息。1994年以来国内掀起了对小波分析研究的热潮，小波分析在损伤检测、信号去噪和图像压缩等方面有了长足的发展。文献[24-26]研究了小波变换在损伤探测方面的应用；朱希安等[27]综述了小波分析的研究现状；李宏男等[28]则论述了小波分析在土木工程领域的应用；刘希灵等[29]使用离散小波变换对岩石SHPB实验中的信号进行去噪，得到精确的重构信号；刘立伟[30]利用小波变换对木材应力波缺陷进行了检测；燕永峰等[31]使用修正萨道夫斯基公式和多频带小波包系数，利用Matlab语言编程，提出了一种新型的爆破振动信号波形预测模型；李林[32]使用小波分析研究应力波在粘弹性杆中传播，对波形进行了预测和可视化。

下面介绍小波变换分析粘弹性波传播问题。

连续小波变换的定义：

(16)

A>0,a和b分别为伸缩和平移因子，Ψ(t)为母小波,满足容许性条件

(17)

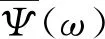
为了研究粘弹性波传播的衰减和弥散特征，需分析应力波信号的相位和幅值信息，连续小波采用复数小波，母小波使用Gabor小波。

一维Gabor小波函数定义为

(18)

傅里叶变换为

(19)

式中 关于γ的取值，多数文献均取值5.336[33,34]，di Lanza等[35]研究发现，当γ=5.336时，Gabor连续小波变换的群速度值与Pochhammer-Chree理论计算值比较吻合。

在使用小波变换求解波传播问题时，由于小波变换的理论知识较为复杂抽象，初学者不易上手；且计算过程中，实际运算量较大，对计算环境和计算速度要求较高；最重要的是小波基的选取尚未有系统规范的方法，有待科研人员进一步探索。

3 Laplace变换法研究粘弹性波

3.1 Laplace变换法的基本原理

Laplace变换是在Fourier变换的基础上进行研究，为弥补Fourier变换处理非平稳信号上的不足而提出。其数学原理是在Fourier变换的基础上乘一个衰减因子e- a t，具体过程如下。

(20)

(21)

式中a为实数，i为虚数单位，s为复数，令s=a+iw。

由于粘弹性波传播过程中的波动控制方程是一组偏微分方程，可以通过求偏微分方程的技术来对粘弹性波的传播问题进行求解，而Laplace变换是将时域的波动偏微分方程转换为拉氏域的常微分方程求解的一种方法，早期便有学者提出使用Laplace变换对波传播问题进行求解，但限于将像函数转换为原函数的过程十分复杂，研究进展缓慢。且Laplace变换是一种半解析法，需要根据初始条件和边界条件结合波动控制方程求解。近年来由于计算机技术的高速发展，发展了很多Laplace反变换的技术，Dubner等[36]将Laplace变换与有限傅里叶余弦变换结合起来进行Laplace变换的数值反演；Durbin[37]对Dubner的方法进行改进优化，提出了一种精确的拉普拉斯变换数值反演方法；Wilcox[38]为拉普拉斯变换的数值计算提供了一个有效的基础，以解决传统解析方法无法解决的瞬态问题；Honig等[39]提出了一种基于Durbin的傅里叶级数展开的拉普拉斯变换数值反演方法；Abate等[40,41]研究了多精度的Laplace数值反演；Cohen[42]整理出版了相关书籍。Laplace反变换的高速发展，为使用Laplace变换技术求解粘弹性波的传播问题提供了便利。

国内使用Laplace变换法对粘弹性波传播问题的研究不多，周风华等[43]研究了SHPB实验中的粘弹性波传播问题，采用Laplace变换处理波动方程,用数值反变换技术对像函数进行Laplace逆变换，改进FT反变换算法，并证明了其方法的有效性。周风华等[44]采用特征线法和Laplace变换法处理一维粘弹性波传播问题，比较其结果表明,沿特征线差分方法可以有效处理强间断在粘弹性介质中的传播，是一种便利、高效的数值分析方法；而Laplace变换方法具有简洁和快速的特点，对于一些简化的问题，结合数学分析软件可以迅速得到初步答案。郑宇轩等[45]采用Laplace变换处理SHPB实验中涉及粘弹性试件内部应力非均匀性问题，并给出了数值反变换解，该方法对分析应力波导致混凝土等非均质脆性材料的破坏问题提供了一个新的解决途径。王建等[46]采用Laplace变换法处理桩基应力波传播问题，将混凝土桩基简化为粘弹性介质中的一维粘弹性杆，建立杆中一维粘弹性应力波传播的控制方程，结合桩基两端的耦合边界条件对控制方程进行Laplace变换和数值反变换，得到了时间域的应力波形。

本文以一根长为L的粘弹性试件为研究对象，x为粘弹性试件的Lagrange坐标，时间为t,试件左端受到冲击荷载，采用简单的Kelvin模型描述粘弹性材料的力学特性，其由一个弹性构件和粘性构件并联而成，如图1所示。

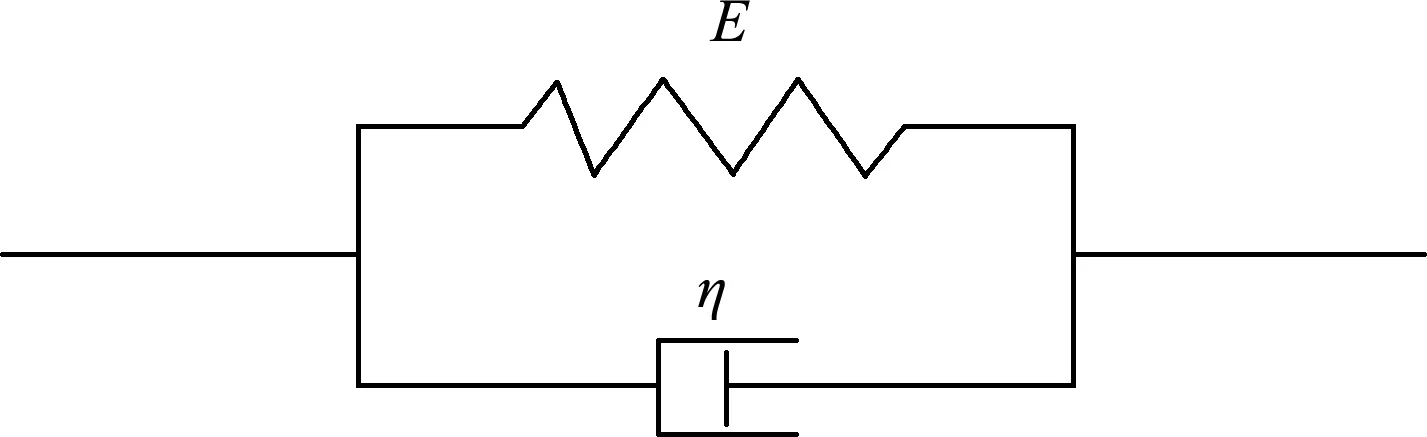
图1 Kelvin模型

材料本构方程

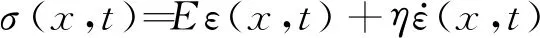
(22)

因材料最初处于静止状态，故其初始条件为

(0

对所有未知数函数的时间变量做Laplace变换，变换后的Laplace像函数在其上划横线表示，像函数的变量为s。对偏微分方程(1，2，22)进行Laplace变换，结合初始条件(23)可得

(24，25)

(26)

(27)

(28)

方程(28)的通解为

(29)

式中

(30)

虽然Laplace反变换近年得到了长足的发展，但该技术还不是十分成熟。

3.2 Laplace变换在粘弹性波中应用研究

Laplace变换法在处理粘弹性应力波传播问题方面，由于Laplace变换能够准确定位应力波任意时刻、任意点的波动情况，故在多个领域占有重要的地位。下面从地震波、基础应力波和球面应力波几个方面介绍其应用。

3.2.1 Laplace变换在地震波中的应用

当地震波通过复杂的建筑介质时，建筑物表现出内在的粘弹性特性，为准确描述地震波在粘弹性介质中的传播特征、衰减和弥散情况，刘良坤等[47]使用Laplace变换研究框架-剪力墙的地震响应，建立框架-剪力墙的动力分析模型，并通过算例与有限元模型验证所建立动力模型的正确性；李保[48]利用Laplace变换求解拱结构的地震响应,通过工程实例不同的工况来验证该方法的准确性，结果证明利用Laplace变换求解大跨度拱结构的地震激励响应问题时，比振型迭加法求解该问题更简捷，精确度更高。

3.2.2 Laplace变换在基础应力波中的应用

由于建筑物的基础多为钢筋混凝土结构浇筑，钢筋混凝土不同于一般的刚性或者弹性材料，多表现为粘弹性特征，故在研究基础受外界激励时，基础内部多为粘弹性波。王健[46]采用Laplace变换研究桩基中应力波传播问题，使用Laplace变换对控制方程和定解条件求解，并用数值反Laplace变换对像函数作反变换，得出空间各点速度和应力等物理量的精确值，是对传统方法(特征线法和传播系数法等)的一种补充；祝彦知[49]使用Laplace变换对土体受集中荷载的情况进行分析,求解土体的位移、应力和应变粘弹性解，进一步完善了空间半无限体的计算理论；王新辉等[50]运用Laplace变换研究双层地基固结问题，在Laplace 逆变换中运用Stehfest算法进行数值求解，最终计算结果与实测沉降结果相符，证明了该方法的正确性和适用性；郑长杰等[51]在研究大直径管桩在粘弹性土层中的竖向动力响应时，利用Laplace变换对控制微分方程进行求解，研究结果表明，在大直径管桩完整性试验中应考虑横向惯性效应；熊辉等[52]基于Laplace 变换，对层状地基中桩土横向振动阻抗计算问题进行了研究，并通过实例分析，验证了该方法的有效性和可行性。

3.2.3 Laplace变换在球面应力波中的应用

卢强等[53]对球面应力波传播特征进行研究，利用Laplace变换对球面波波动方程进行求解，得到Laplace域中的粒子速度、位移、应力和应变等物理量，采用基于Crump算法的Laplace数值逆变换方法分析了上述物理量的传播特征，发现折合速度势和折合位移势的峰值在波传播过程中逐渐衰减,这与理想弹性理论给出的折合速度势和折合位移势不随传播距离变化的结论不同。刘干斌等[54]基于Biot波动方程，研究在粘弹性饱和土中嵌入部分密封壳的球形空腔的瞬态响应，利用Laplace变换和Durbin提出的数值反Laplace算法求解轴对称表面荷载和流体液压的瞬态响应；夏才初等[55]基于西原模型，使用Laplace变换和逆变换，推导出了圆形隧道粘弹-粘塑性的解析解，分析围岩位移及应力等物理量随时间变化的规律，结合工程实例进行验证，建议采用让压支护技术来保证围岩和衬砌的稳定性，为圆形隧道建设提供一定的理论依据。

4 粘弹性波传播分析方法的比较

以上几种处理粘弹性波传播问题方法的使用条件及其各自的优劣总结如下。

(1) 特征线有限差分法。计算过程需使用材料的本构方程、初始条件和边界条件；该方法比较成熟[3]，计算结果准确，接近理论解，且能准确刻画粘弹性波的传播、反射和相互作用的特征，能够有效地处理强间断波在粘弹性介质中的传播，具有便利和高效的特点；但当试件尺寸过大时，计算过程较多，耗时较长，成本较高，对分析大尺寸混凝土等试件达不到预期效果。

(2) 传播系数法。计算过程需要用到材料的本构方程，不需要初始和边界条件；在使用该方法计算细长杆(即忽略横向惯性效应)的粘弹性波的传播时十分快捷，过程简单，误差在3%左右[19]；但对大杆(波长不显著大于杆径)，则需考虑横向惯性效应，计算公式冗长，过程复杂，求解困难。

(3) 波传播实测信息的反分析法。该方法不需要使用材料的本构方程、初始和边界条件；求结构冲击力十分简单，求得传递函数成为该方法的关键。由于传递函数仅与结构尺寸和材料特性有关，可先用已知力和结构响应来求得传递函数，再以此求解该系统的未知冲击力大小；但是由于在求解传递函数时，建立符合实际的有限元模型至关重要，建模过程中始终存在一定差异，造成误差较大，卢静涵等[22]在算例中存在高达13%的误差。

表1 几种波传播方法对比分析Tab.1 Comparative analysis of several wave propagation methods

(4) 小波变换分析法。计算时需要使用材料的本构方程、初始和边界条件；小波分析具有在时域和频域都显示信号细节的能力，通过平移和伸缩的可变视窗口能够聚焦到信号的任何细节部位，得到信号的瞬时特征，进行时域和频域的信号处理，在非平稳信号的处理方面具有不可替代的地位；且其计算结果精确，误差在1%～3%[28,32]。但小波变换入门困难，实际运算量较大，同时在最优小波基的选取方面，缺乏系统规范的方法。

(5) Laplace变换法。计算过程需要使用本构方程和初始边界条件；该方法能简洁快速地计算出试件的全场波动解，计算结果与特征线有限差分法基本一致，验证了该方法的有效性和精确性，且在求解某一点或某一时刻的波动问题时，计算效率高(与特征线法和传播系数法比较)[44]，同时该方法在处理大尺寸的混凝土材料的波动问题时也能快速地得到全场波动解；但数值反Laplace变换是近年随着计算机技术的发展而崛起，发展时间较短，还存在很多不足，如将波动问题从时域变换到S空间上后，可能导致后期的扰动信号对前期的波动状态产生影响，可参考文献[43]的解决方案。

5 结 论

通过对几种求解方法的优劣分析以及对Laplace变换在粘弹波中应用的研究，可知Laplace变换法相较于其他几种算法，具有十分快捷、高效和精准的特点，可求解出应力波在任意时刻、任意点的应力应变和粒子速度等物理量；尤其对于混凝土这类大试件，其他几种分析方法对其求解都比较困难或者成本较高，而Laplace变换法在求解混凝土应力波传播问题中具有其独有的优势，可用粘弹性本构模型拟合混凝土材料的动态应力应变关系[56]，将混凝土视为粘弹性介质，结合初始和边界条件进行求解。其发展趋势还可扩展到对梁和柱类大型混凝土等非均质脆性材料及飞机渡轮等缓冲材料和军工爆炸材料的冲击及碰撞问题进行求解，为这类问题提供了一个新的解决途径。