考虑动水压力和流固耦合的库水-坝体-地基系统建模与动力分析

赵佳耀， 黄 丹， 徐业鹏， 王 磊

(河海大学 力学与材料学院，南京 211100)

1 引 言

目前，我国已建或在建的大型水利工程大多处于地震多发区[1]，面对地震的强破坏性和不可预知性，结构物极易受到损伤破坏并导致水灾、滑坡和海啸等灾害发生。因而针对水工建筑物系统开展抗震分析非常重要，广受力学和相关工程领域关注。

在水工建筑中，水体由于地震而产生的动水压力会显著影响结构的动力响应，不可忽视。20世纪30年代，Westergaard[2]针对水工建筑物中最典型的坝体所受的动水压力开展研究，并在假设坝体和地基均为刚性的条件下，提出了垂直坝面动水压力模型。随后，众多学者对坝面动水压力问题进行了深入研究。如Zhou等[3]通过振动台试验研究了地震引起动水压力的发展过程；王忠阳[4]首次采用等效替代方式模拟地震引发的库水作用，通过某闸墩模型研究该方法的作用机理，并验证了试验方法的可行性与适用性；王铭明等[5,6]通过振动台上坝体-库水系统动力模型试验与数值计算结果对比，表明附加质量法夸大了库水对坝体结构的动力响应。

随着数值方法研究的深入和计算机技术的发展，基于数值模拟开展动水压力和流固耦合计算成为另一个重要的途径。如陈怀海等[7]基于级数展开和线性叠加原理，提出了求解坝面动水压力的计算方法；Maity等[8]通过有限元离散迭代实现流固界面的相互作用。Zeinizadeh等[9]提出在开口收缩缝中应用动水压力的算法来研究收缩缝水压力对拱坝的影响。针对工程结构的流固耦合问题，文献[10，11]对流体-结构-地基相互作用问题开展数值分析；熊春宝等[12]对地基中的热-水-力耦合问题进行了研究；Fu等[13]考虑了混凝土面板堆石坝-库水的耦合效应；申跃奎等[14]则基于有限体积法对结构表面流固耦合问题进行了研究。针对坝面动水压力，邱流潮等[15]分析了地震作用下，拱坝上游坝面动水压力的影响因素；杜修力等[16,17]提出了一种计算直立坝面上地震动水压力的时域公式，并研究了动水压力对坝体地震反应的影响。此外，文献[18-21]基于比例边界有限元法开展了坝面动水压力求解和模拟研究。

在已有研究基础上，本文通过结合动水压力和罚函数耦合算法，在不增加自由度的条件下降低网格精度的要求以提高求解速度，构建分析地震作用下库水-坝体-地基系统动力响应的数值模型和方法，经过模型验证后，应用于某重力坝系统动力分析。该模型可全面考虑坝体和地基的弹塑性、坝体-地基间相互作用以及地震动激励下的非线性动力响应。

2 模型和方法

2.1 力学模型

将库水受地震作用引起的动力响应转化为动水压力施加于坝体。构建库水-坝体-地基耦合系统的简化力学模型如图1所示。

设地震作用下结构受到的动水压力P满足波动方程：

(1)

式中c为水中声速，2为拉普拉斯算子。

边界条件为

S1： 流固耦合面

(2)

S2： 底面

(3)

S3： 无限远处，采用无反射边界

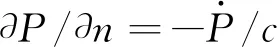
(4)

S4： 自由表面处，无压力作用

P=0

(5)

2.2 流固耦合界面处理

为分析地震作用下库水-坝体-地基系统的整体动力响应，在耦合界面处遵循几何相容条件以及力平衡条件：

vf=vs=∂u/∂t|χ，Ff+Fs=0

(6，7)

式中vf和vs为耦合界面水流速度和固体材料速度；Ff和Fs为流体和固体结构作用在耦合界面的力。

在数值模型中引入罚函数算法处理流固耦合界面，如图2所示。界面间作用力为

(8)

图1 库水-坝-地基力学模型

式中Z为穿透量，ξ为阻尼系数。

引入罚函数算法可在不增加自由度的条件下，与利用显式积分求解含有惯性项接触问题时的控制方程协调。结合动水压力模型和罚函数耦合算法，可加快计算收敛，在保证计算精度的前提下提高计算效率。

对结构模型进行离散，考虑耦合效应的系统运动方程可表示为

(9)

同时，在边界上满足：

(10)

式中

(11)

(12)

(13)

(14)

式中S为变换矩阵，将压力转换为节点力作用在耦合面上，Re表示计算域。

结构物受地震作用时，阻尼的取值影响到结构物的地震动力响应，在分析中，采用Rayleigh 阻尼，其表达式为

C=α·M+β·K

(15)

对于Rayleigh阻尼，其与临界阻尼的比值为

(16)

通过计算结构物前2阶自振频率ω1和ω2及阻尼比ξ得到待定系数α和β。

2.3 模型验证

以文献[22,23]的库-水模型试验为原型，验证本文计算模型和方法的可行性。模型如图1所示，长L1=15 m，H=180 m的矩形坝体，右侧水体L2=900 m，此时右侧边界可近似为无反射边界，网格共计164700个，网格尺寸大小为1 m。

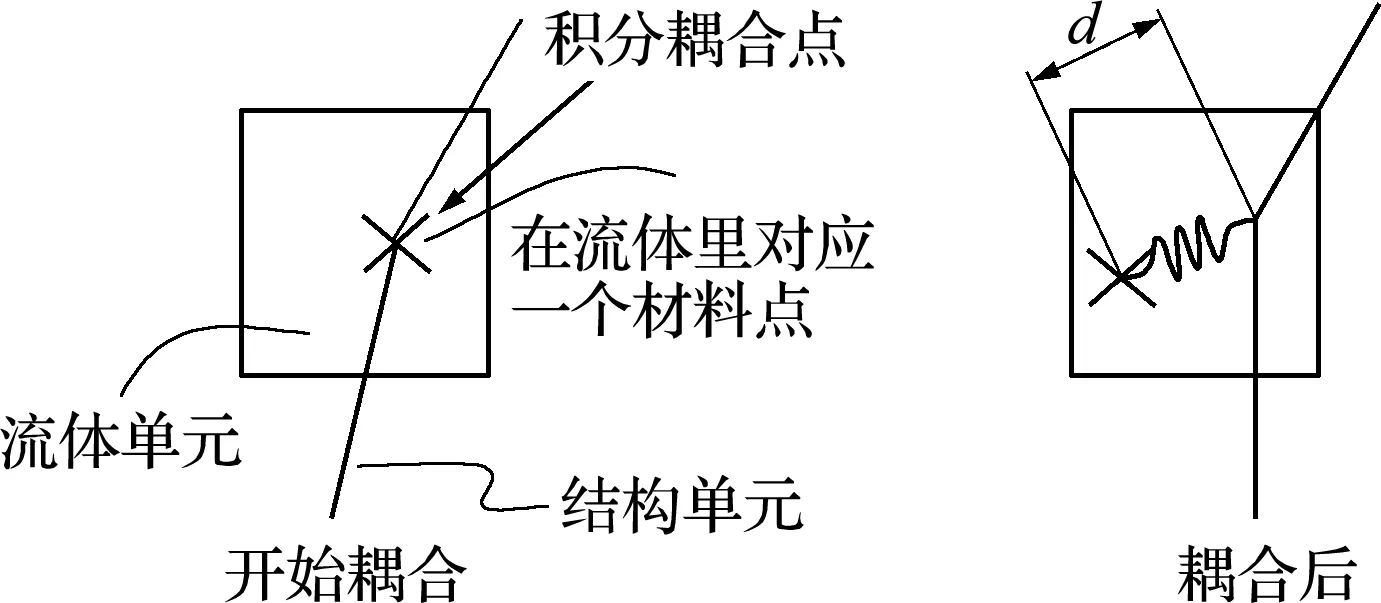
图2 耦合方法

与文献工况一致，地震水平加速度时程曲线采用EI-Centro波，地震波峰值加速度为0.2784g[22,23]，地震加速度从模型底部输入，坝基为固定端。时间步长取值遵循courant=cΔt/Δx≤1，其中Δt为时间步长，Δx为最小网格尺寸。

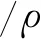
3 算例分析

以某混凝土重力坝结构为例，应用本文模型和方法分析其地震响应。坝高为100 m，坝顶长度为909.26 m。基岩以河湖沼泽相砂岩、泥岩以及含煤底层为主。本文主要研究结合动水压力模型与罚函数流固耦合算法分析库水-坝体-地基系统的动力响应，简化地基中的软弱夹层和陡倾破碎带，整体分析模型如图5所示。模型边界从半无限域土体中选取有限域土体作为计算区域，为消除地震作用下边界反射对结构物的影响，对模型底部和两侧设置粘弹性人工边界[24]。坝体及地基材料采用

图3 位移结果对比

图4 动水压力结果对比

Drucker-Prager准则描述，材料参数列入表1。

为验证本文方法对于各类结构的普适性，同时为便于与理论解、试验和工程实测值对比，对计算结果进行无量纲化处理。

对坝高与压力作无量纲化处理，y为高程，h为水深。图6为计算所得坝面处动水压力沿高程方向与Westergaard解析解[2,6]的对比。可以看出，坝面动水压力分布情况与Westergaard解析解[2,6]吻合很好，且符合实际规律，表明本方法模拟动水压力问题的可行性和高精度。

为分析地震作用下动水压力与库水自振频率的关系，对坝踵处动水压力进行傅里叶变换，对频率与压力作无量纲化处理。图7结果表明，在自振频率附近，坝体受动水压力影响较大，尤其在一阶自振频率处，坝面上动水压力出现峰值，其后动水压力迅速减小，规律与文献[6，19]的结果一致，再次表明本文结合动水压力模型和罚函数耦合算法模拟坝体结构的地震响应是可行的。

表1 材料参数

图5 库水-坝体-地基数值模型

图6 坝面动水压力分布

为进一步验证本文方法对实际库水-坝体-地基系统动力学分析的适用性，结合新丰江水库实测地震数据[25]，对坝体系统动力响应进行分析。

坝体地震加速度沿坝高的分布如图8所示。其中实测值为1967年坝基东西向地震记录，试验模型比为1∶200[25]。本文模拟结果与大坝实测值和模型试验值均吻合较好，在坝踵处模拟结果相对试验值更接近实测值，进一步验证了本文模型的可行性和模拟精度。其中，坝体顶部和坝踵处的加速度时程曲线如图9所示，在地震作用下，坝体顶部水平加速度相对坝踵处放大约7倍，与文献[25]实测数据吻合。可见，本文方法能适用于库-水相互作用下坝体系统抗震动力响应，且采用罚函数描述流固耦合界面，计算效率较高。

为对比静水压力和考虑流固耦合动水压力作用下系统的动力响应，取坝顶处的顺河向位移时程曲线如图10(a)所示。在不考虑库水动态作用时，位移响应峰值为0.0301 m，与考虑动水压力和耦合情况下的位移峰值0.0539 m相差79%。图10(b)对比了分别采用库水-坝体模型与考虑地基影响下的库水-坝体-地基模型时坝顶位移的时程曲线。可以看出，考虑地基时振动规律与库水-坝体模型一致，但幅值变化较大。对比表明，在地震荷载作用下进行坝体动力分析时，模型考虑动水压

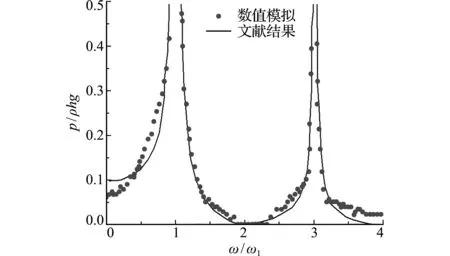
图7 坝踵处动水压力频响曲线

图8 最大加速度分布

力与流固耦合以及考虑地基对库水-坝体系统的影响是必要的。

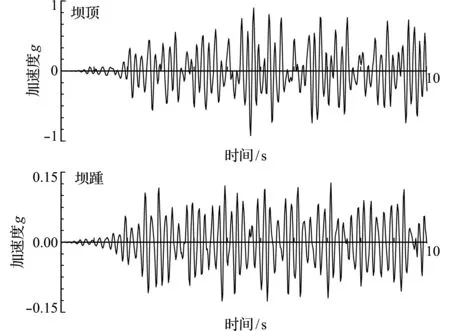
图9 坝体加速度时程曲线

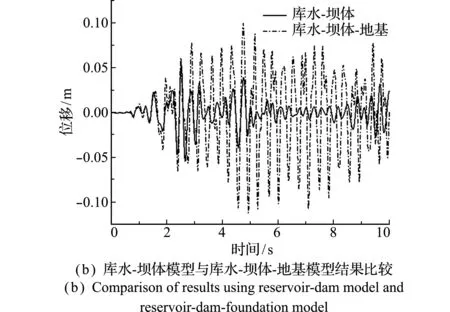
图10 坝顶位移时程曲线比较

4 结 论

本文结合动水压力模型和罚函数耦合算法，考虑地基和坝体结构的接触以及边界效应，构建了动水压力和流固耦合作用下的库水-坝体-地基地震响应分析模型与方法。结论如下。

(1) 结合动水压力模型与罚函数耦合算法可以有效地模拟流体-结构间相互作用，得到的动水压力作用和动位移与试验结果及解析解吻合较好。同时，采用该模型在不增加自由度的同时降低了网格精度要求，加快收敛，可提高计算效率。

(2) 构建的计算模型可在时域求解库水-坝体-地基系统的地震响应，坝面动水压力和坝踵动水压力频响曲线规律均与文献及实测结果一致，表明本文模型适用于分析地震作用下的库水-坝体-地基系统动力响应。

(3) 在进行流固耦合作用下的水工结构等地震分析时，考虑动水压力与流固耦合以及地基对库水-坝体系统的影响是必要的，本文在流体-结构-基础系统的地震动力分析方面的思路和措施可供参考。