考虑坝体柔性的重力坝坝面地震动水压力计算
2019-05-30胡志强郭维东
王 毅,胡志强,郭维东
(1.沈阳农业大学水利学院,辽宁 沈阳 110866; 2.大连理工大学建设工程学部,辽宁 大连 116024)
一直以来,大坝-库水动力相互作用问题备受关注,尤其是在地震频发地区,水利枢纽的安全与之密切相关。针对大坝-库水系统的动力相互作用研究,主要体现在如何准确计算地震作用下坝面所受动水压力。对于动水压力的研究,源于Westergaard[1]提出的动水附加质量理论,其忽略水的可压缩性,推导出坝前水深恒定的二维刚性重力坝受水平方向地震动激励情况下坝面动水压力解析计算公式。而后,Chopra[2]在其基础上推导了受不同方向地震动激励,考虑库水可压缩性的二维重力坝动水压力在频域和时域中的解析解。随着有限元方法(FEM)的不断发展,Chopra等[3-7]对坝面动水压力进行了深入的研究,采用FEM模拟了水的可压缩性及库底和岸坡的吸收作用对坝面动水压力的影响,并把其应用从二维重力坝推广到三维拱坝。然而,限于大坝-库水系统中库水的半无限特性,采用FEM时往往需要离散足够长库水区域,导致计算机内存占用量和计算量大;另一方面,在计算中无法实现对整个半无限域库水的完整离散,客观上需要一个合理的截断边界,并施加一定边界条件来模拟半无限域。起初的研究局限于使用Sommerfeld辐射条件[8],Sharan[9]通过添加阻尼项,提出了一种更为有效的边界条件,只需离散较短库区水域,数值计算结果表明其能够保证足够精度,并可减少部分计算量。为了解决FEM中库区离散量较大的问题,Hanna等[10]用边界元方法(BEM)对大坝-库水动力相互作用进行了研究,结果表明,在一定的库区形状下,BEM能够有效地求解坝面动水压力,且大大降低了计算量,但只能对于少数规则库区形状才能找到其基本解。
以上研究多基于刚性坝面假设,即未考虑坝面柔性的影响。事实上,在强震作用下,高坝的柔性是进行大坝-库水相互作用分析中不可忽略的因素。由于坝体柔性的存在,在一定程度上能够削弱地震作用下库水对坝体的动力作用,从而降低坝体内部响应。为了研究柔性包括坝体柔性和库底柔性对结构响应的影响,Bouaanani等[11]首先在频域中推导了刚性坝面动水压力,并考虑了库底柔性的影响;而后Bouaanani等[12]采用模态分析方法研究了坝体柔性的影响,在频域中求解了坝面动水压力,同时考虑了水库边界的吸收效应,得到了相对完善的结果。但其采用有限元的基本思想,需要离散部分计算库区和添加人工辐射边界条件,在一定程度上增加了计算量,对计算效率的提高有限。随着数值方法的发展,出现了一种新的数值方法——比例边界有限元方法(SBFEM)[13]。它基于BEM的思想,仅对求解域的边界进行离散,域内采用比例分配的思想进行解析求解,且无需BEM中复杂的基本解,由于其解形式可自动满足无穷远处辐射条件,对于求解半无限域波动问题优势明显。在SBFEM框架下,对大坝-库水相互作用的研究也有了初步进展。Lin等[14-17]基于SBFEM推导了坝面的频域动水压力,对混凝土坝动力响应进行了详细研究,结果表明该方法在处理半无限域库水时不仅能够大幅度降低计算量,且能保证足够精度,同时对库水的可压缩性和库底吸收可方便考虑。Wang等[18-20]采用SBFEM对无限域库水边界进行离散,坝体内部仍然采用传统的FEM进行求解,提出了一种半无限域的开放边界条件,得到了二维重力坝动水压力时域计算结果。
本文在此基础上,综合考虑坝体和库底柔性的影响,提出一种基于SBFEM和FEM耦合理论的求解大坝-库水系统中坝面动水压力计算方法,并通过算例对该方法进行验证,分析坝体柔性、库水可压缩性和库底反射系数对坝面动水压力的影响。
1 大坝-库水系统基本方程
1.1 大坝基本运动方程
在地震动作用下,考虑到库水对大坝的动力相互作用,大坝时域运动方程用标准FEM可描述为
(1)

由式(1)可知,若能确定在地震作用下坝面所受的动水压力,即可得到大坝的整体动力响应。对于刚性坝体,坝体内部不产生相对加速度,迎水面各点的动水压力仅与激励地震动相关;而考虑坝体柔性的影响,坝面所受动水压力与大坝自身运动密切相关,因此动水压力与坝体响应是耦合关系。对其进行解耦,是在考虑坝体柔性影响下对大坝-库水相互作用进行求解的关键。
1.2 库水基本运动方程
利用SBFEM对半无限域的库水进行离散,把相似中心O设在水库下游无穷远处,如图1所示,此时水库的上下表面趋于平行,据SBFEM基本理论,仅离散水库与大坝的交界面即可实现对整个求解水域的高精度模拟,无需添加人工截断边界,从而极大地简化对库水的离散。

图1 库水-重力坝耦合示意图
假设库水为可压缩小扰动线弹性液体,库水在整个求解域中满足如下方程:
(2)
对于整个库区,忽略库水表面微幅重力波的作用,可认为库水表面在地震过程中不发生变化,库水表面的边界条件简化为
p=0
(3)
坝水交界面上满足应力连续边界条件
(4)

库底和岸坡的边界条件采用Fenves等[5]提出的吸收边界条件:
(5)

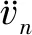
无穷远处的边界条件为
(6)
由于本文采用SBFEM,因此,式(6)是自动满足的,在计算中不需要对此边界进行特殊处理。
使用加权余量方法对库水的控制方程和边界条件进行离散,可得到在SBFEM框架下的频域动水压力方程,文献[14]给出了其详细的推导过程及其求解过程,动水压力的频域结果可表示为
(7)

1.3 大坝-库水系统的耦合运动方程
在频域中,把动水压力控制方程代入大坝运动基本方程,可得到考虑坝体柔性影响的大坝-库水系统的频域运动方程

(8)
其中Mb(ω)=AMa(ω)

方程(8)清晰地表达了大坝-库水相互作用的解耦频域运动方程,通过对坝面动水压力的SBFEM求解,得到动水压力的附加质量计算公式,实现对大坝-库水系统动力相互作用的求解。运用方程(8)可得到柔性坝面下的坝体响应,回代方程(7)即可对坝面动水压力进行求解,同时也实现了对坝体柔性的考虑。
1.4 程序实现方法
本文采用自编FORTRAN计算程序,实现了考虑坝体柔性的重力坝坝面地震动水压力的计算。计算步骤如下:
步骤1网格剖分。采用商业软件ANSYS对整个坝体进行有限元网格剖分,网格剖分可根据需要进行相关细化。此时需注意,在数据输入时标记迎水面上的节点编号,为计算SBFEM框架下的特征矩阵Ma(ω)提供便利。
步骤2SBFEM特征矩阵计算。通过提取坝面节点单元信息,在SBFEM计算体系下,求解迎水面上特征矩阵Ma(ω)。
步骤3频域运动方程求解。通过通用等参单元FEM代码组装方程(8)中的总体刚度与质量矩阵,在FEM框架下实现对方程(8)的求解,得到坝体各个节点的频域响应值。
步骤4坝面动水压力计算。通过方程(7)求解坝面动水压力,实现对坝体柔性的考虑。
2 算例验证
为了验证所提方法的有效性,选取文献[12]中的Pine Flat二维重力坝为计算模型,所有计算参数均采用文献[12]中的资料。其中,坝高为121.92 m;截面形状为三角形;上游面垂直,下游面坡度为1∶0.8;大坝混凝土弹性模量为35 GPa;质量密度为2 400 kg/m3;泊松比为0.2;黏滞阻尼比为0.1;满库状态下,坝前水深H=121.92 m;库水质量密度为1 000 kg/m3;水中压力波波速为1 440 m/s。大坝网格剖分如图2所示,坝体离散为192个四节点平面单元。地震动激励为水平方向的频域单位地震动。

图2 Pine Flat 重力坝网格剖分
2.1 刚性坝面
图3和图4分别给出了刚性坝面动水压力频响函数曲线和动水压力沿高程分布曲线,图中g为重力加速度;pstat为静水压力;ω1为水库的第一阶自振频率;无量纲频率为实际频率与ω1的比值。文献[11]给出的是不考虑坝体柔性和考虑库水可压缩性情况下的封闭形式的理论解。本文采用SBFEM计算得到的动水压力频响函数曲线和动水压力沿高程分布,均与文献[11]的理论解高度一致,表明了SBFEM在求解动水压力上的有效性,为后面的柔性坝面结果对比提供了可靠的保证。

图3 刚性坝面动水压力频响函数曲线

图4 刚性坝面动水压力沿高程分布曲线

图5 柔性坝面动水压力频响函数曲线

图6 柔性坝面动水压力沿高程分布曲线
2.2 柔性坝面
图5和图6分别给出了柔性坝面动水压力频响函数曲线和动水压力沿高程分布。计算结果表明,本文采用SBFEM计算的结果与文献[12]数值解吻合良好,仅在库水的第一阶和第二阶自振频率附近存在微小的差别,在其他频率区间内,计算结果与文献[12]数值解较为一致,尤其在工程人员最感兴趣的低频范围内,计算结果精度非常好。
2.2.1坝体柔性的影响
从图3和图5刚性坝面与柔性坝面动水压力频响函数曲线的对比中,发现在地震作用下坝体柔性对坝面动水压力的影响显著。由于坝体柔性的存在,坝面所受动水压力发生显著变化,在水库前两阶自振频率内,坝面的动水压力急剧增大;而在水库高频阶段,坝面的动水压力降低(水库的自振频率ωn=(2n-1)πc/(2H),其中n=1,2,…)。这是因为在水库低阶自振频率附近,坝体内部也产生了较大的与地震动激励相同方向的相对加速度;在高频阶段,坝体本身产生了与地震动激励相反方向的相对加速度运动,从而降低了坝体柔性对结构响应的影响,表明坝体自身的弹性在一定程度上削弱了地震动所引起的作用在坝面上的动水压力。
从坝面动水压力沿高程分布(图4和图6)可以看出,坝体柔性对坝面动水压力分布形式产生了一定的影响。其影响随着库底反射系数的减小而逐渐增大,尤其在高频阶段。由于坝体柔性的存在,坝面动水压力不再符合刚性坝面动水压力的抛物线分布形式,随着激励频率的提高,坝面上的动水压力峰值会从坝踵逐渐向坝体中上部移动。
2.2.2库水可压缩性的影响
频响函数计算结果(图3和图5)表明,库水可压缩性对坝面动水压力的影响明显。不考虑库水可压缩性时,坝面所受到动水压力与地震动激励的频率无关,在图3和图5中可以表示为数值为初始值的水平直线,即不考虑库水可压缩性时,坝面动水压力是一定值,且与考虑库水可压缩性时的初值相等。当前计算结果表明在低频阶段,库水的可压缩性会减小对坝面动水压力的估计,相反在高频阶段却明显加大了坝面动水压力的估计,对于合理地考虑坝面所承受的动水压力具有非常不利的影响。鉴于当前的研究结果均不能单一确定库水的可压缩性对坝体的响应究竟有何种定性的影响,但能够确定的是库水的压缩性对大坝-库水系统存在重要影响,因此在计算中需要分不同的计算频率进行详细考虑。
2.2.3库底反射系数的影响
动水压力频响函数结果(图3和图5)和动水压力沿高程分布(图4和图6)均表明,不论是刚性坝体还是柔性坝体,库底反射系数对坝面动水压力的影响规律均趋于一致,即随着反射系数的降低,坝面所承受的动水压力也逐渐降低。这表明水库的柔性,即库区的吸收作用,以及坝体柔性对大坝-库水动力相互作用影响明显,且有利于提高坝体的抗震性能,因此合理地确定库底反射系数能够更加合理有效地求解大坝-库水系统动力相互作用问题。
综上,从柔性重力坝的计算结果可以看出,SBFEM得到的结果与文献[12]数值解非常吻合,表明本文所提方法对求解频域大坝-库水相互作用问题非常有效。从刚性坝面的结果来看,SBFEM得到的结果与文献[11]理论解极为吻合,表明SBFEM对求解半无限域波动问题的优越性。在本文算例中,无需离散半无限域库水的整个区域,仅仅离散了库区与大坝交界面上的17个节点,相比FEM离散整个水域和BEM离散整个边界均可降低计算量以及计算机存储的压力,且并未损失计算精度。
3 结 论
a. 本文提出了一种求解重力坝坝面地震动水压力的计算方法,其能方便考虑坝体柔性和库底柔性的影响,且能保证计算效率和计算精度。
b. 坝体柔性对坝面动水压力的影响依赖于地震动激励频率。低频阶段,坝体柔性能够增大系统的响应,相反在高频阶段其能降低系统响应。坝体柔性也影响坝面动水压力分布的形式。刚性坝面情况下,坝面动水压力呈现出规则的抛物线分布;柔性坝面情况下,动水压力的分布形式趋于不规则化,尤其在高频阶段表现更为明显。
c. 库底反射系数对坝面动水压力具有较为明显的影响,随着反射系数的减小,坝面所承受的动水压力会随之降低。
