纤维分级对漂白云杉木浆纤维悬浮液屈服性能的影响

王 灿 李金隆 王 琪 邵宇正 沙九龙，* 王双飞

（1.广西清洁化制浆造纸与污染控制重点实验室，广西大学轻工与食品工程学院，广西南宁，530004；2.浙江冠豪新材料有限公司，浙江嘉兴，314200）

纸浆纤维悬浮液是非均相混合物，其中纤维被认为是固相。在造纸工业中，从蒸煮工序到纸张成形都涉及到不同浓度纤维悬浮液的流动过程，而研究纤维悬浮液的流变特性对纸浆的输送、搅拌、混合乃至设计优化高速纸机流送系统都具有重要的现实意义［1-3］。

纸浆悬浮液主要由纤维组成，通常纤维直径为15～30μm，长度为1～3 mm，具有较高的长径比。随着浆浓的增大，纤维开始缠绕并形成尺寸为1～2 cm的絮团［4］。纤维交织的密集程度可以用集聚因子N（Crowding Number）表示［5］，其表示以单根纤维长度为直径的球形区域内纤维的总数目，见式（1）。

式中，l是纤维长度（m），δ是纤维粗度（kg/m），φ是纤维悬浮液质量浓度（g/L）。

Martinez等［6］在N=16处定义了一个凝结集聚因子“Ngel”，用来表征植物纤维初始形成交织网络时的临界絮凝浓度，该临界浓度也被称为凝结点φg。当N＜16时，纤维间未形成稳定交织结构；相反，当N＞16时，纸浆悬浮液中纤维之间碰撞搭接，开始发生交织并形成连续的纤维网络，这种网络结构具备一定抵抗外部流体剪切力的物理强度，这个物理强度即为纤维悬浮液的剪切屈服应力τy［7］。研究结果［8-10］显示，剪切屈服应力与纤维悬浮液质量浓度Cm呈指数式函数关系（见式（2），a和b为常数），与纤维长径比A、弹性模量E也有定量关系（见式（3），Cv为纤维悬浮液体积浓度，c为常数），此外还会随纸浆卡伯值、纤维挺度和pH值的增大而增大，但随温度的升高而降低。

同剪切屈服应力类似，压缩屈服应力Py描述了纤维絮团抵抗外部流场挤压作用的结构强度［11］，当外部流场的压力超过絮团的压缩屈服应力Py时，纤维絮团会发生坍缩，纤维内部接触点增多，交织更密集，絮团浓度急速提高［12］。国内外研究者通过大量的研究，在植物纤维领域建立了压缩屈服应力Py与纤维悬浮液质量浓度φm之间的指数关系式（见式（4），α、β为常数）［13-14］。

考虑到压缩屈服应力和剪切屈服应力都是基于纤维网络的弹性形变，纤维网络的压缩屈服特性很可能与剪切状态下的屈服特性有关。纤维悬浮液的剪切屈服应力与压缩屈服应力的比值被称为Froude数，其作为一个无量纲数可以用来表示剪切屈服应力与压缩屈服应力间的关系［13］。

目前，有关纸浆纤维悬浮液Froude数的研究鲜有报道，从纤维絮团的屈服特性角度，Froude数作为衡量剪切屈服应力与压缩屈服应力耦合权重关系的指标亟待探索。为此，本研究从分级纤维悬浮液屈服特性的角度出发，利用沉降和流变实验来测量纤维悬浮液的压缩屈服应力与剪切屈服应力，建立了压缩屈服应力、剪切屈服应力与纤维悬浮液集聚因子的关系，并进一步探讨了二者比值与纤维形状系数、集聚因子的关系。所得结论对于在屈服应力耦合作用下，构建纸浆纤维絮凝分散倾向与纤维尺寸间的影响机制具有重要的理论和实际意义。

1 实验

1.1 材料与仪器设备

漂白云杉木浆，购自广西贵糖集团有限公司；BauerMc-Nett纤维筛分仪，奥地利PTI公司生产；KajaaniFS300纤维质量分析仪，芬兰Metso公司生产；R/S-CC型流变仪，选配V3-60-30桨式旋转叶片（直径30 mm，高度60 mm，4片），美国Brookfield公司生产；L260-5011标准纸浆疏解机，瑞典Lorentzen＆Wettr公司生产；有机玻璃量筒，购自广西美辰亚克力制品有限公司。

1.2 纤维分级处理

将干燥后的浆片浸泡在蒸馏水中24 h，然后用疏解机分散5 min，制成均匀的纤维悬浮液。随后在纤维筛分仪中分别用16、30和50目筛网对云杉木浆纤维进行连续分级。从筛网保留下的纸浆中取样，未通过16目筛网的纤维记录为R16，通过16目筛网后且留着在30目筛网上的纤维记录为P16/R30，以此类推得到P30/R50，未分级的纸浆为原浆。使用纤维质量分析仪测量纤维长度、直径和粗度。根据TAPPI T227 om-04测量分级前后纸浆的游离度。

1.3 实验方法

1.3.1沉降实验

沉降实验在内径100 mm、高度约为400 mm的玻璃量筒中进行。将纸浆用去离子水稀释成集聚因子分别为2.5、5.0、7.5、10.0、12.5和15.0的纤维悬浮液。将纤维悬浮液用玻璃棒充分搅拌混合均匀，进行沉降实验（6 h），直到沉淀层与上层清液的分界线清晰可见。在沉降过程中，随着沉降时间的变化记录沉降高度，每次实验需要进行3次。所有实验均在室温下进行。

1.3.2凝结点及压缩屈服应力测量

通过平衡间歇沉降实验确定凝结点［15］，每个量筒底部承受的压力（Pbase，i，mPa）为：

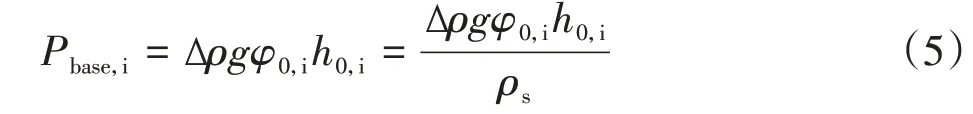
纤维沉积层的平均质量浓度（φav，i，g/L）计算方程为：

式中，Δρ是液固密度差（kg/m3），g为重力加速度，φ0，i是纤维沉积层初始体积浓度（%），φ0，i是纤维沉积层初始质量浓度（g/L），ρs是纤维密度（实验用漂白云杉木浆纤维密度为1520 kg/m3），h0，i和hf，i分别是每个实验样本的初始和最终沉降高度（mm）。构建φav，i关于Pbase，i的关系并进行线性拟合。曲线延伸至φav，i轴上的截距即为凝结点。而压缩屈服应力Py的值则可以近似等于量筒底部所受压力的1 2，即：

1.3.3剪切屈服应力测量

剪切屈服应力使用流变仪测量。测量之前，纸浆纤维悬浮液在100 s-1的剪切速率下预剪切180 s，再静置60 s，以得到相同的初始条件。预剪切和静置后，以10 r/min的转速剪切40 s，并记录扭矩值随时间的变化。随后，利用以下方程将每次启动时的峰值扭矩转换为剪切屈服应力τy［16］：

式中，Tm为测量的峰值扭矩（N·m），D为转子叶片的直径（m），H为转子叶片的高度（m）。

2 结果与讨论

2.1 不同纤维组分的形态

对纸浆进行了纤维形态表征分析，结果如表1所示。由表1可知，与原浆和短纤维组分浆相比，长纤维组分浆的纤维长度、直径和粗度最大。纤维长度及直径为数均值。

2.2 沉降过程

不同集聚因子N下原浆的沉降特性如图1所示。由图1可知，在沉降的初始阶段，纤维悬浮液以较快的速度沉降，短时间内沉降高度急剧变化。从图1还可观察到，随着集聚因子N的增大，纤维沉降速度降低。这主要是由于集聚因子N的增大使得纤维间的相互交联程度增大，从而阻碍了它们的沉降。分级所得纸浆纤维悬浮液在相同的集聚因子N范围内也具有同样的沉降性质（数据未显示）。

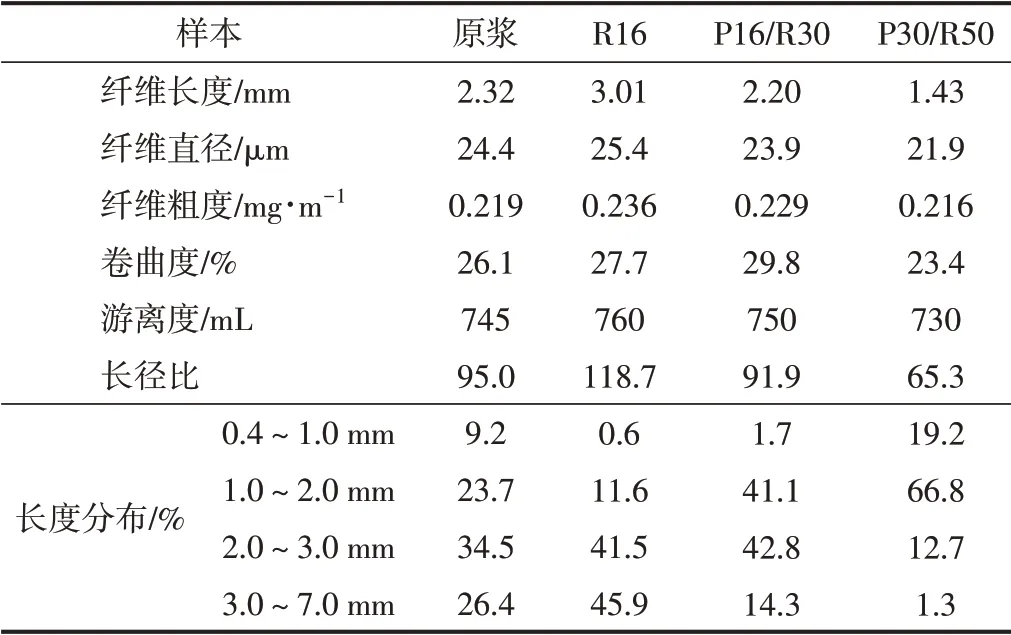
表1 纸浆纤维样品的纤维形态

图1 不同集聚因子N下原浆的沉降特性

分级前后纤维悬浮液的最终沉降高度与集聚因子N的函数关系如图2所示。由图2可知，长纤维组分浆的最终沉降高度较低，主要是因为在相同集聚因子N下，其纤维数目较少。随着集聚因子N的增大，云杉木浆的纤维悬浮液最终沉降高度呈指数增长，这主要是由于纤维相互作用发生了变化，纤维沉积层的网络结构开始发生不可逆的形变。

2.3 凝结点

对于分级纸浆纤维，测量了不同质量浓度纤维悬浮液的沉降过程并绘制φav，i与Pbase，i的关系图，并用线性方程拟合。拟合方程线在φav，i轴上的截距就是凝结质量浓度φg。图3为原浆φav，i与Pbase，i的关系图，分级前后纤维悬浮液φav，i与Pbase，i的拟合方程及其相关系数见表2。

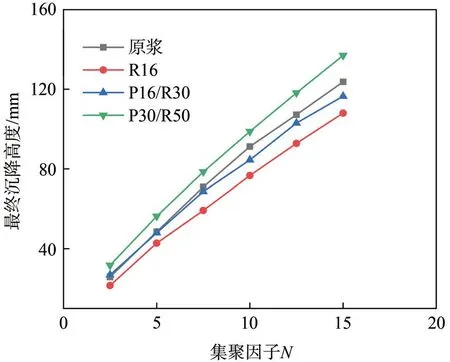
图2 不同集聚因子N下纤维悬浮液的最终沉降高度

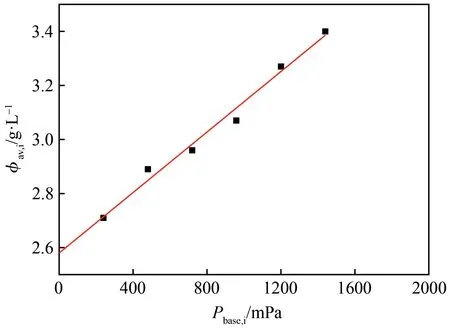
图3 原浆凝结点的测定

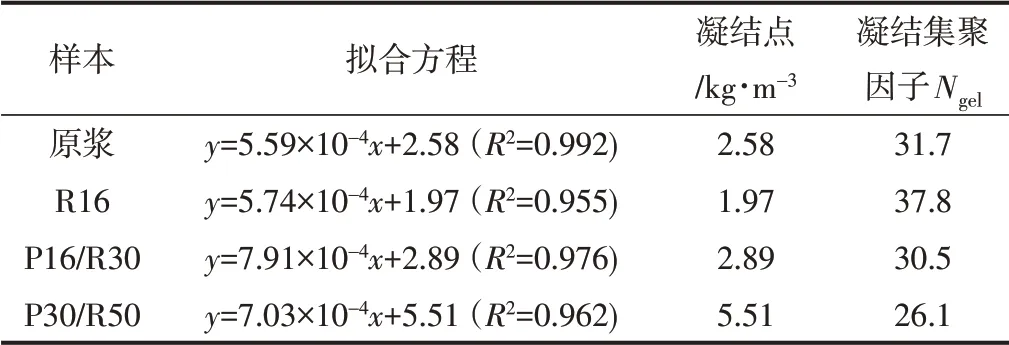
表2 分级前后纤维悬浮液的φav,i与P base,i的拟合方程及凝结点

由表2可知，分级前后4种纤维悬浮液的凝结点在1.97～5.51 kg/m3之间，与Martinez等［6］的研究结果一致。从表2还可以看出，R16纤维悬浮液的凝结点最低，说明长纤维组分悬浮液更容易达到临界浓度，形成网络结构。由式（1）可计算得到4种纤维悬浮液相应的凝结集聚因子Ngel在26.1～37.8之间，其随纤维长径比A的变化趋势如图4所示。由图4可知，云杉纤维悬浮液的凝结集聚因子Ngel随纤维长径比A的增大近似呈线性增大，回归模型的相关系数较高（R2=0.967）。此外，用沉降法测量的凝结集聚因子均大于理论凝结集聚因子(Ngel=16)，这主要是由于凝结点的计算方法不同导致［17］。

2.4 压缩屈服应力

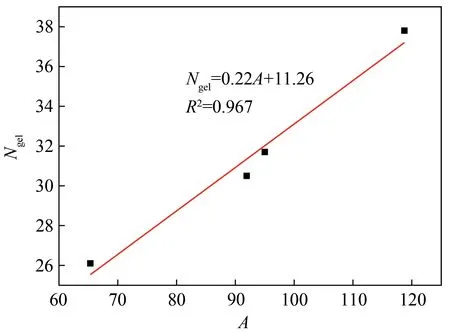
图4 云杉木浆纤维悬浮液纤维长径比A与N gel的函数关系

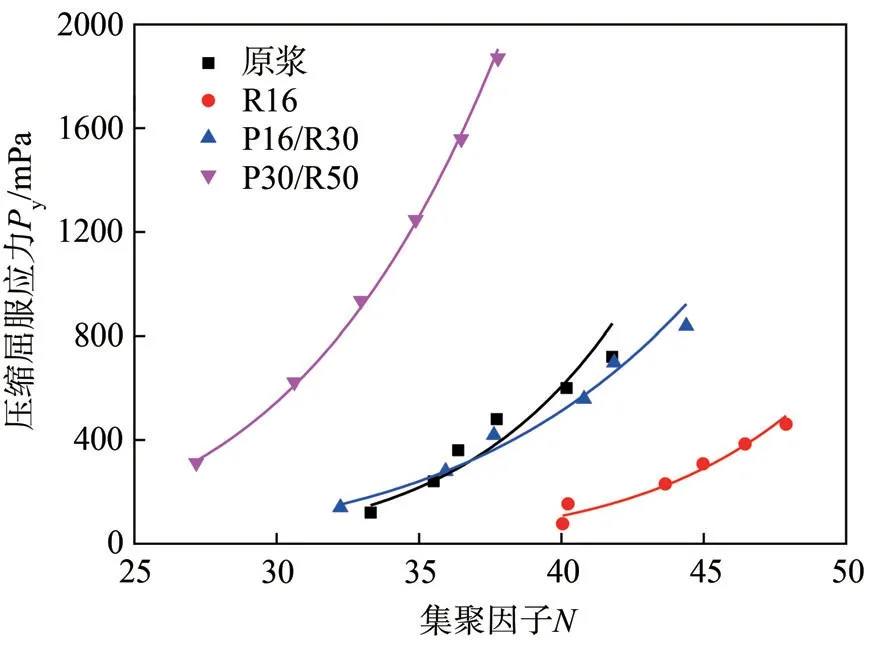
图5 分级前后纤维悬浮液的压缩屈服应力P y与集聚因子N的关系曲线

表3 分级前后纤维悬浮液的压缩屈服应力P y与集聚因子N的拟合函数

图5为分级前后纤维悬浮液压缩屈服应力Py随集聚因子N的变化曲线。由图5可知，压缩屈服应力Py随集聚因子N的增大呈指数式增大。其原因是较大集聚因子N的纤维有利于纤维网络的构建。与短纤维组分相比，P30/R50纤维组分在同样的集聚因子N下表现出的网络强度最大。在一定集聚因子N范围内，压缩屈服应力Py与集聚因子N间满足指数函数关系：

式中，a和b为常数。

表3是分级前后纤维悬浮液的压缩屈服应力Py与集聚因子N的拟合函数。从表3可以看出，回归模型的相关系数（R2）均较大，这意味着拟合出的函数模型与实验测量的压缩屈服应力Py能够很好地吻合。

2.5 剪切屈服应力

图6为分级前后纤维悬浮液的剪切屈服应力τy随集聚因子N的变化曲线。同压缩屈服应力Py变化曲线相似，随着集聚因子N的增大，剪切屈服应力τy相应地增大。这是因为随着纤维悬浮液集聚因子N的增大，纤维交织更加紧密，纤维网络结构的强度更强，从而增大了剪切屈服应力τy［18］。从图6可以发现，在相同的集聚因子N下，纤维长径比越小，剪切屈服应力τy越大。其原因是在相同集聚因子N下，纤维长径比越小，纤维数越多，纤维之间的接触点就越多，由此纤维网络就越稳固，破坏这个网络结构所要施加的剪切力就越大。通过数据拟合可得到剪切屈服应力τy与集聚因子N的指数函数：

式中，m和n是常数。

分级前后纤维悬浮液的剪切屈服应力τy与集聚因子N的拟合函数关系见表4。

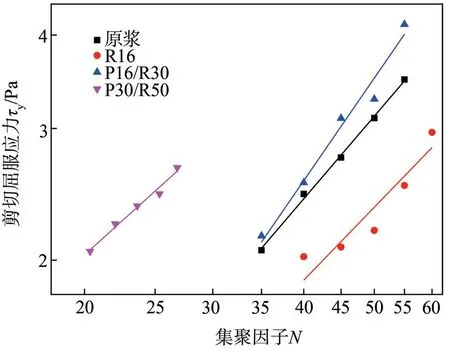
图6 分级前后纤维悬浮液的剪切屈服应力τy与集聚因子N的关系曲线

表4 分级前后纤维悬浮液的剪切屈服应力τy与集聚因子N的拟合函数

2.6 剪切屈服应力τy与压缩屈服应力P y耦合相关性

通过计算可以得到分级前后纤维悬浮液剪切屈服应力τy与压缩屈服应力Py的比值，即Froude数（P30/R50在集聚因子N为35～60下的Froude数由拟合数据推导得出）。Froude数计算方法如下：

图7显示了分级前后纤维悬浮液Froude数与集聚因子N之间的关系。由图7可知，随着集聚因子N的增大，Froude数呈非线性下降，且趋势逐渐放缓。当集聚因子N=60时，各纤维悬浮液样本的Froude数逐渐趋于一致，这意味在纤维网络开始搭建的阶段，其承受外部压力的能力弱于抵抗剪切应力的能力，而随着集聚因子N的增大，纤维网络的承压能力提高，且比抗剪切力性能提高得快，并最终趋于稳定。

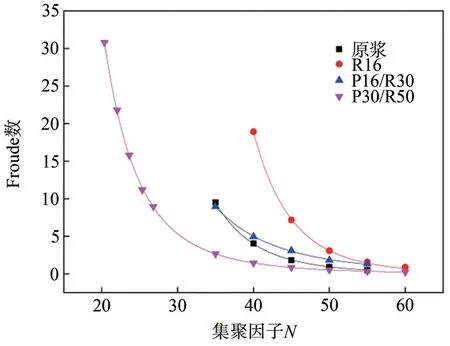
图7 分级前后纤维悬浮液的Froude数与集聚因子N的函数关系

3 结 论

采用沉降和流变实验，研究了纤维分级对漂白云杉木浆纤维悬浮液屈服性能的影响。分级前后云杉木浆纤维悬浮液的凝结集聚因子在26.1～37.8之间且凝结集聚因子随着纤维长径比的增大近似呈线性增大。在所研究的集聚因子范围内，压缩屈服应力和剪切屈服应力都与集聚因子呈指数关系，且在同一集聚因子下，纤维长径比越小，屈服应力值相对越大。Froude数（剪切屈服应力与压缩屈服应力的比值）随集聚因子的增大而逐渐降低，并趋于稳定。