珊瑚砂地质条件下钢板桩结构可靠性分析
2020-10-27吴伟东
韩 意, 张 磊,吴伟东
(1. 安徽科技学院 建筑学院,安徽 蚌埠 233030; 2. 中交水运规划设计院有限公司,北京 100007)
在一些缺乏大型施工设备的岛屿国家,钢板桩由于施工便捷经常被用作护岸结构。岛屿国家经常碰到珊瑚砂地质,珊瑚砂与传统石英砂的力学指标差异较大,其强度低、易碎、力学指标离散性大。因此在珊瑚砂地质条件下,钢板桩的结构设计不能单纯运用《码头结构设计规范》(JTS167-2018)[1],还应运用结构可靠度理论进行安全复核。
结构可靠度计算最初建立在全概率法(水准III法)理论上,由于数理理论本身的局限性,全概率法在结构可靠性研究中发展缓慢。近似概率法(水准II法)由于其计算方法简单,能够满足工程精度要求,发展比较迅速,其中一次二阶矩法应用最广泛,包括中心点法、验算点法、映射变换法、实用分析法。随着计算机技术的发展,Monte Carlo模拟的应用也越来越受到重视。采用JC法分析钢板桩结构的可靠性[2]。
我国对珊瑚砂的研究一般依托于我国南海海域的相关工程。主要通过岛屿中建造的各种码头、仓库等基础设施,进行珊瑚砂混凝土的力学试验、钢板桩等围挡结构的设计与施工、浅基础设计与施工等工程应用方面的研究[3]。李捷等[4]开展了与国家海洋权益息息相关的珊瑚砂力学性质研究,通过收集的资料总结了当前研究中的不足,并提出了建议。孙宗勋[5]通过研究说明珊瑚砂是一种特殊的岩土介质,主要成分是珊瑚和海洋生物碎屑,具有孔隙比高、强度低和摩擦角高等力学特点。佘殷鹏等[6]通过扫描电镜观测、直剪试验和颗分试验,研究了珊瑚砂的剪切特性,得出珊瑚砂具有结构疏松、孔洞明显的特征。张晋勋等[7]通过原位沉降监测和室内试验得出珊瑚砂地基的压缩特性及沉降变形规律,提出地层长期沉降的计算公式和参数确定方法。
钢板桩结构是一种在工程结构中广泛使用的支护体系,起到挡土和挡水的作用,具有环保、使用简单、施工效率高等特点[8-9]。钢板桩结构设计要关注结构受力及耐久性。钢板桩结构计算主要包含:前墙踢脚稳定性、锚碇墙稳定性、锚碇墙到前墙距离、前墙内力、锚碇墙内力、锚杆直径。钢板桩耐久性主要通过预留腐蚀裕量、加阳极保护及刷涂层实现。我国水运工程钢板桩设计施工主要依据《码头结构设计规范》(JTS167-2018)[1]。在国际工程中,可以参考的设计标准还有欧标 Eurocode 3:DesignofSteelStructures, Piling[10]和Eurocode 7:GeotechnicalDesign[11],英标BS 6349-2-2010:MaritimeWorks.CodeofPracticefortheDesignofQuayWalls,JettiesandDolphins[12],美国陆军工程兵团手册EM_1110-2-2504:DesignofSheetPileWalls[13],澳标AS-2159-2009:Piling-Design-And-Construction[14]。
以马尔代夫机场扩建项目为案例,通过原位测试取得岩土体的物理力学指标。运用可靠度理论分析了珊瑚砂力学指标的高变异性对钢板桩结构稳定可靠度的影响,得出一些有益的结论。
1 结构可靠度理论
结构的可靠性是指在规定时间和规定条件下,结构能完成规定功能的能力。结构的可靠度和失效概率是结构可靠性理论中非常重要的两种概念。其中结构可靠度是结构可靠性的度量,一般采用β表示,而失效概率是指结构不能完成规定功能的概率,一般采用Pf表示[1]。
设随机向量X= (X1,X2,……,Xn)的联合密度函数为:fX(x1,x2,……,xn)=fX(x),由此随机向量表示的结构功能函数为Z=g(X)。则结构的失效概率为:
(1)
式中:F= {x|g(x) < 0}表示结构的失效域。
计算工程结构可靠度的方法和相关研究较多。李荣庆等[15]针对《板桩码头设计与施工规范》(JTJ292-98)修订的需要,将板桩结构的参数作为随机变量,对其统计特性进行了分析,提出了板桩结构的可靠度分析方法,并将结果与国内14个板桩结构的可靠指标进行了计算比较。本文选用规范中建议的JC法进行结构可靠性计算。
运用JC法进行结构可靠度计算,极限状态方程为:
Z=g(X1,X2,……,Xn)=0
(2)

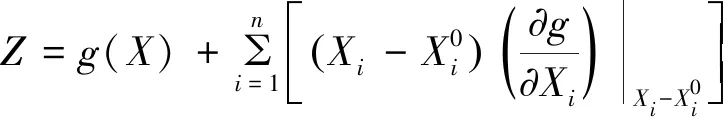
(3)


(4)

(5)

求解UXi=(Xi-μXi)/σXi方向余弦的相反数,即:

(6)
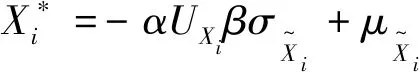
2 珊瑚砂的力学特性
2.1 珊瑚砂物理性质
珊瑚砂是一种由海洋生物和珊瑚碎屑组成的,呈松散状态、形状不规则、多空隙、颗粒分布不连续的钙质土。由于其特殊的物理性质,导致其强度、破碎规律、压缩和蠕变等力学性质与常规的石英砂有显著区别。珊瑚砂的颗粒密度范围一般在2.70~2.85 g/cm3之间,大于石英砂的平均颗粒密度2.65 g/cm3。珊瑚砂的孔隙比在0.54~2.97之间,比石英砂的范围高出许多[6]。
2.2 珊瑚砂力学指标
1) 珊瑚砂的颗粒强度。珊瑚砂颗粒在外力作用下发生破碎是珊瑚砂的一个重要特性, 这一特性在压缩和剪切过程中表现得非常明显。珊瑚砂在围压大于100 kPa 时就会产生可测定的破碎, 而且随围压的增大破碎加剧。而石英砂只有在围压大于1 600 kPa时才有轻微的破碎产生[6]。
2) 压缩特性。珊瑚砂与石英砂的压缩特性存在显著差别,主要表现在石英砂在被压缩初期会产生较大变形,并且会以很快的速度达到稳定状态,而珊瑚砂在被压缩初期沉降比较小,但是会随着时间推移发生很缓慢的长期沉降。珊瑚砂的颗粒破碎被认为是产生这种现象的重要原因之一。珊瑚砂的压缩性高,其压缩指数大约是石英砂的100倍[6]。
3) 黏聚力。根据国内外学者的试验研究,珊瑚砂有微小的黏聚力,通常数值在10 kPa左右[6]。
4) 内摩擦角。在相同的孔隙比和相近的颗粒分布条件下,珊瑚砂的摩擦角明显大于石英砂的摩擦角,可达59°,这主要是由于珊瑚砂颗粒间存在较高的矿物摩阻力、颗粒破碎及其重新排列。珊瑚砂内摩擦角随着颗粒粒径的增大而增大。由于珊瑚砂的强度较低,容易破碎,现实工程中,珊瑚砂内摩擦角呈现较强离散性,变异系数较大。
5)渗透性。珊瑚砂的渗透系数随着粒径和级配的变化而变化。粒径较小,颗粒均匀,级配较好的珊瑚砂渗透性较低。反之,粒径较大,级配相对较差的珊瑚砂渗透性一般较高。如果将珊瑚砂作填海工程的回填料,地基处理工艺会对珊瑚砂的渗透性造成较大的影响。
3 板桩结构稳定可靠性极限状态方程
根据《码头结构设计规范》(JTS167-2018)中6.3.2条规定,前墙入土深度应满足“踢脚稳定”要求[1]。
前墙结构“踢脚稳定”极限状态方程为:
Z=MR-∑MGi-∑MQj
(7)
式中:MR为板桩墙前被动土压力的标准值对拉杆锚碇点的稳定力矩;MGi为永久作用标准值产生的作用效应,包括前墙后土本身产生的主动土压力的标准值和剩余水压力的标准值对拉杆锚碇点的“踢脚”力矩;MQj为可变作用效应,通常是码头地面可变作用产生的主动土压力的标准值或墙前波吸力的标准值对拉杆锚碇点的“踢脚”力矩。
在计算极限状态方程(7)的可靠度指标时,可以采用JC法、Monte Carlo法、映射变换法等,计算结果精度都比较高,文中在计算钢板桩结构可靠度时采用JC法。
4 工程实例分析
马尔代夫机场改扩建项目具有珊瑚砂地质条件,典型护岸断面形式如图1所示。岩土勘察结果显示,该地区珊瑚砂的内摩擦角变异性较大。珊瑚砂内摩擦角φ统计值及根据内摩擦角φ计算的各作用力矩的统计值见表1。根据K-S检验,内摩擦角φ服从正态分布。工程案例主要是分析珊瑚砂内摩擦角的高变异性对钢板桩结构可靠性的影响。由板桩前墙稳定性的计算公式(7)可知,前墙稳定性与墙前被动土压力产生的力矩MR、自重产生的主动土压力力矩MG1、均载产生的主动土压力力矩MG2、剩余水压力产生力矩MG3和波吸力产生的力矩MG4有关。同时MR、MG1、MG2都与珊瑚砂的内摩擦角φ相关,因此这三个变量是相关的。

图1 马尔代夫机场改扩建项目典型护岸断面Fig. 1 Typical shore protection section of Maldives airport expansion project

表1 各作用力矩的统计值Tab. 1 Statistics of the moments
为了简化计算,案例中剩余水压力产生力矩MG3和波吸力产生的力矩MG4取定值,分别为588.08 kN·m和60.17 kN·m。
为选择最符合自重产生的主动土压力力矩MG1分布的模型,分别用皮尔逊Ⅲ分布、甘布尔(Gumbelf)分布和对数正态分布对MG1进行拟合,拟合结果见图2。
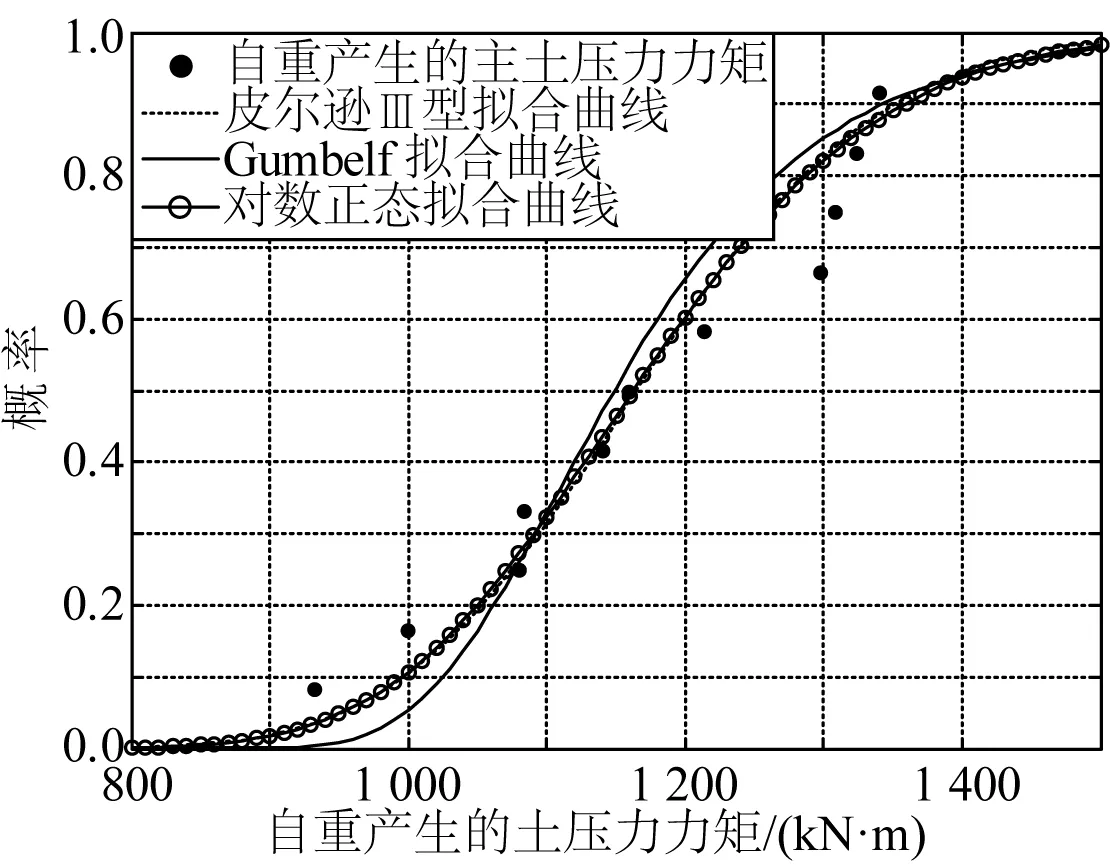
图2 MG1的三种曲线拟合Fig. 2 Fitting curves of MG1
对各分布拟合的自重产生的主动土压力力矩MG1求取拟合方差,结果见表2。

表2 MG1曲线拟合的方差Tab. 2 Variance of MG1 fitting curve
从以上拟合结果看,自重产生的主动土压力力矩MG1分布更符合对数正态分布。同理,对均载产生的主动土压力力矩MG2和墙前被动土压力产生的力矩MR分别进行以上三种曲线拟合,拟合结果表明,MG2符合甘布尔分布,MR符合皮尔逊Ⅲ分布,曲线拟合结果见图3和图4。

图3 MG2的三种曲线拟合Fig. 3 Fitting curves of of MG2

图4 MR的三种曲线拟合Fig. 4 Fitting curves of of MR
根据表1,计算求得各力矩的均值μ和标准差σ见表3。

表3 变量统计参数表Tab. 3 Statistical parameters of variables
运用可靠度理论中的JC法以及前墙结构“踢脚稳定”极限状态方程(7),计算护岸板桩踢脚可靠度指标,可得可靠指标β=3.023 5,对应的失效概率Pf=0.001 2。
根据《码头结构设计规范》(JTS167-2018)中6.3.2条规定,前墙入土深度应满足公式γ0[∑γG1MG1+γG3MG3+ψ(γG2MG2+γG4MG4+……)]≤MR/γR,在珊瑚砂内摩擦角φ取推荐值27°时进行计算,求得持久组合设计低水位的前墙稳定力矩设计值(上式中MR/γR)与踢脚力矩设计值(上式中γ0[∑γG1MG1+γG3MG3+ψ(γG2MG2+γG4MG4+……])的比值为1.13。具体系数取值及计算结果见表4和表5。

表4 按照规范分项系数取值Tab. 4 Partial factor in accordance with the codes

表5 按照规范计算的结果Tab. 5 Calculation results in accordance with the codes
上述计算结果表明,采用《码头结构设计规范》(JTS167-2018)进行稳定性计算满足结构安全时,考虑将珊瑚砂内摩擦角作为变量,进行踢脚稳定性可靠度复核,踢脚稳定性可靠度不能满足《港口工程结构可靠性设计统一标准》(GB50158-2010)的β≥3.5的要求(安全等级二级)[16]。
在上述计算过程中,将珊瑚砂的黏聚力C取为0,实际工程中珊瑚沙的黏聚力虽然很小,但也是存在的。荀涛等[17]在研究中指出,珊瑚砂的黏结力参数为2.56 cm3/s2,颗粒之间接触面积很小,黏结力较低。在考虑珊瑚砂黏聚力为10 kPa的情况下,依然采用JC法以及前墙结构“踢脚稳定”极限状态方程(7),计算可靠度,得到可靠指标β=3.078 8,对应的失效概率Pf= 0.001 0,具体的计算结果比较见表6。

表6 是否考虑黏聚力计算结果比较Tab. 6 Comparison of whether or not considering the cohesive force
计算结果表明,是否考虑珊瑚砂的黏聚力对钢板桩结构稳定可靠度的影响并不大。
5 结 语
在珊瑚砂地质条件下,钢板桩结构稳定性的计算需要特别关注两点:一是珊瑚砂内摩擦角的高变异性;二是珊瑚砂具有一定的黏性。通过计算分析可以得到如下结论:
1) 设计人员在选取珊瑚砂内摩擦角的推荐值时需要慎重,按照勘察规范给出的推荐值可能偏于危险,对于港口工程,设计人员应同时按照《港口工程结构可靠性设计统一标准》(GB50158-2010)复核结构的可靠度指标。
2) 珊瑚砂具有一定的黏性,但对结构可靠度计算结果影响较小,在进行结构可靠度计算时可以忽略珊瑚砂黏聚力的影响。
珊瑚砂具备良好的渗透性能,研究珊瑚砂作为墙后回填料时的剩余水压力具有指导工程实践的意义;相比于石英砂,珊瑚砂的强度较低,研究珊瑚砂颗粒破碎对其力学指标的影响也具有指导工程实践的积极意义。这两点是珊瑚砂特殊物理性质对结构可靠度影响后续需要研究的内容。
