风机基础TLP平台在波浪中运动性能的CFD数值分析
2020-10-27安筱婷赵伟文万德成
安筱婷,赵伟文,万德成
(上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室 船海计算水动力学研究中心(CMHL),上海 200240)
海上风能作为一种清洁的可再生资源,在陆上资源日益枯竭的今天越来越受到关注,海上风机是人类开发海洋风能资源的载体。随着风能开发向深水发展,支撑风机的载体平台越来越受到关注。深水风机的优势在于深水环境中风速更大,风能更强,且不影响航运,但随着水深的增加,作用在载体平台上的水动力增加,浅水中常用的固定式平台由于造价高、质量大、建造安装难度大、运动性能不适合恶劣海况等原因不再适用。浮式支撑平台可重复使用,造价低,运动性能更好,因而在深水环境中应用广泛。
浮式平台中,张力腿平台(tension leg platform,简称TLP)是目前被广泛应用的一种平台,使用剩余浮力平衡张紧式系泊系统的预张力,具有半顺应半刚性的特点,可抵抗波浪引起的运动,以此为风力发电提供一个相对稳定的环境,减少风力发电机功率的变化对电网的影响。同时TLP自身的直立浮筒结构也为平台提供了良好的运动性能。
目前已有多座TLP实际投入生产使用,此外,研究学者也针对作为风机基础平台的TLP的特性需求,提出了许多设计方案,并针对这些设计方案进行了大量计算与验证。Ren等[1]对一种TLP—海上风机系统进行了1/60比例模型试验,以考察耦合风浪效应,同时还提出了TLP系泊系统的优化方案。Bachynski等[2]考虑100~200 m水深中作业的TLP实际情况,提出了该水深水平中TLP的设计方案。Adam等[3]提出了20~350 m水深中,将TLP作为风机基础平台的设计——GICON©设计。Gao等[4]基于边界元方法,对风机基础TLP 的运动响应和波浪力机制进行了分析。Bilgili等[5]使用全耦合模拟对于单立柱TLP风机的设计参数进行了参数研究。Han等[6]提出了一种半潜式TLP平台(submerged tension leg platform,简称STLP),此平台在作业状态下水线面面积较小,因此具有更佳的动力学性能。
与船舶不同,浮式平台需要长期保持在特定海域进行作业,因此需要系泊系统提供回复力来抑制外界载荷引起的水平运动。另一方面,风机支撑平台也不允许发生过大幅度的运动响应,这样才能保证风机发电正常输出,电网稳定。故要求浮式平台配备相应的系泊系统,以拥有位置保持能力[7]。综上所述,浮式平台工作时,需要响应系泊系统配合。
计算机科学技术的不断发展与数值计算方法的不断优化,使得船舶与海洋工程水动力学计算领域中应用计算流体动力学(computational fluid dynamics,简称CFD)方法进行计算成为可能。使用自主开发的基于开源程序库OpenFOAM开发的naoe-FOAM-SJTU求解器,该求解器可以求解船舶与海洋工程水动力学问题[8]。为了求解系泊结构物的运动响应,刘远传[9]以此求解器的6自由度运动模块为基础,联系了浮式结构物运动与系泊系统的受力,进一步开发出了系泊系统计算模块(naoeFOAM-ms),完善了原求解器的功能。
由于风机平台系统在实际投入使用时海洋环境条件非常复杂,研究不同海况下风机基础平台的运动响应特性对于指导风机系统的设计、保障人身与财产安全、保证风机系统正常工作有着重要意义。模拟中考虑了不规则波的高阶成分,相比于目前已有的工作更贴近海洋环境载荷实际情况。采用naoe-FOAM-SJTU求解器分析了一座STLP的水动力性能,计算了该平台的固有运动性能,并以此为基础分别讨论处于中等水深作业状态下以及极端海况生存状态下的运动响应情况。首先计算了STLP的固有周期,并与已有结果进行对比,验证了求解器的有效性。在此基础上分别研究了STLP在中等海况下和极端海况下的运动响应、平台受到弯矩及系泊张力,研究了在考虑非线性波浪载荷的极端海况下与一般作业海况下STLP的运动响应情况,计算了不同工况中的风机基础所受弯矩及锚链受力情况,并详细展示了流场、速度场信息,分析了高阶波浪成分、不同海况等条件对于STLP运动性能的影响。研究结果表明,naoe-FOAM-SJTU求解器可以有效地模拟TLP平台在波浪中的运动响应问题,还可以详细展示流场信息。
1 数学模型
1.1 控制方程及离散方法
关于OpenFOAM的求解原理和具体求解步骤可参见文献[10]和文献[11],这里作简单概述。文中的数值模拟基于不可压黏性流体,其控制方程为:
·U=0
(1)
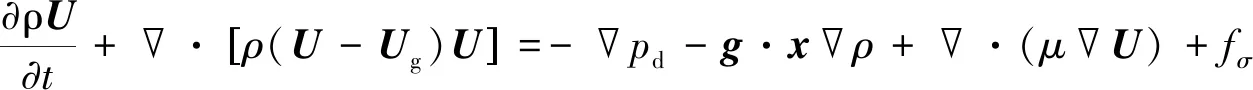
(2)
式中:U代表流场速度,Ug代表网格节点的运动速度;pd=p-ρg·x代表流场动压力,x为网格节点位置;g、ρ和μ分别为重力加速度、流场的密度和动力黏性系数;fσ为源项,表示自由面上的表面张力。
由于模拟中无来流,雷诺数小,湍流的影响可以忽略,因此采用层流模型以提高计算效率,忽略了结构物表面的边界层;采用VOF(volume of fluid)方法捕捉自由面[11-12],定义每个网格中的体积分数,通常选择ɑ=0.5等值面作为流场中的自由面。计算中,采用有限体积法(finite volume method,简称FVM)进行空间离散,使用隐式Euler格式进行时间离散,使用二阶TVD格式进行对流项离散,使用二阶中心差分格式进行扩散项离散。在进行离散化后,应用PISO算法来迭代求解和解耦压力及速度。PISO算法由 Issa提出[13],OpenFOAM中的 PISO算法采用的是由Rhie提出的同位网格方法[14]。最后,可以获得每个时间步的流场变化及最终模拟结果。
1.2 动网格技术
为了模拟平台的运动,需要不断变换计算网格以适应结构物运动对流场的影响。文中采用了naoe-FOAM-SJTU中的动网格技术。当平台发生位移时,网格的形状由移动节点改变,同时保持每个网格节点与相邻网格节点之间的拓扑关系不变。通过求解拉普拉斯方程可以得到网格节点的位置:
·(κXg)=0
(3)
其中,Xg是节点的位移,κ是节点变形系数:
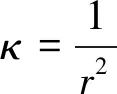
(4)
其中,r是网格中心与移动边界的距离。
1.3 造波与系泊系统模拟
影响海洋工程结构物运动最显著的环境因素之一就是波浪。文中的造波通过开源代码waves2foam[15]实现。waves2foam代码为了产生实际模拟中所需的具体波浪,改变了速度入口边界条件。文中模拟的各种波浪情况均为一阶不规则波(Jonswap谱)。在实践中,线性波浪理论被用来模拟不规则波,例如沿x轴正向传播的长峰不规则波的波面升高[7]:

(5)
式中:Aj为第j个单元波的波幅,ωj为第j个单元波的圆频率,εj和kj分别为相应的随机相位角及波数。波幅与波谱关系为:
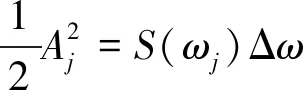
(6)
Jonswap波谱公式为:

(7)
式中:H1/3和T1分别为波浪的有效波高和平均波浪周期,峰值增强因子记为γ。
使用弹簧模拟方法来模拟STLP的垂向系泊系统,具体实现利用了naoe-FOAM-SJTU中的系泊系统求解模块[8]。弹簧模拟方法把STLP的垂向系泊系统等效为只可拉伸不可压缩的一根弹簧,且不考虑弹簧自身的重力以及流场力,弹簧模拟方法目前被广泛应用于TLP类平台运动响应计算中。
弹簧模拟方法的基本原理为胡克定律:
F=kΔl
(8)
其中,k是弹簧的弹性系数,在naoeFOAM-ms的字典文件中给定;F为张力结果,即系泊系统供给浮式结构物的回复力;弹簧的伸长量记为Δl,程序中即为系泊缆实际长度(系泊点与锚泊点的距离)与系泊缆初始长度之差。在系泊系统求解模块中,t-1时刻的系泊力是t时刻的边界条件,参与6自由度运动方程求解,得到本时刻的结构物位置,在锚泊系统中通过系泊点位置(与浮式结构物的位置有关)即可获得下一时间步的系泊力,作为外力参与6自由度运算。
2 计算模型设定
文中的计算模型参考Han等[6]的工作,风机(NREL-5MV)[16-17]、风机支撑平台与8条系泊缆共同组成风机发电系统,如图1所示。STLP作为风机的水下支撑平台,由中心立柱、4个垂直立柱、水平浮筒和斜撑构成,见图2。计算域布置如图3所示,垂直和水平浮筒完全淹没在平均海平面(MSL)下,吃水为20 m,计算域深度为100 m。模拟中坐标轴原点o设置在STLP的水线面中心,三条坐标轴遵循右手螺旋法则,z轴垂直向上。

图1 风机系统示意Fig. 1 Diagram of turbine system
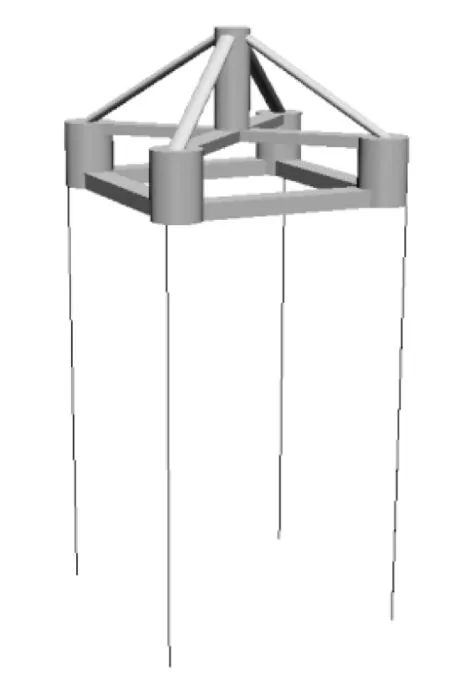
图2 STLP示意Fig. 2 Diagram of STLP
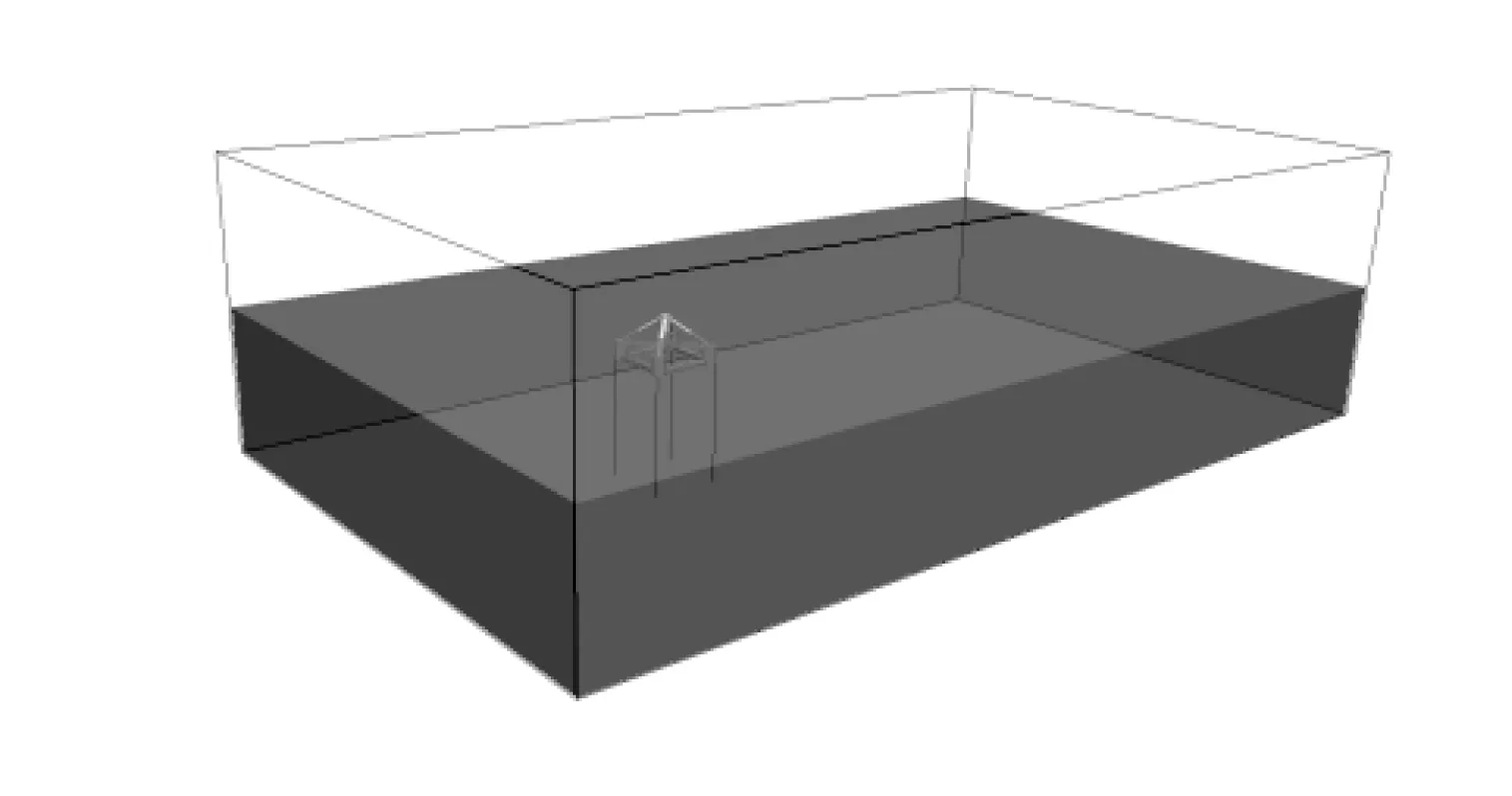
图3 计算域布置示意Fig. 3 Diagram of calculation domain
限制平台运动的锚链系统主要参数如表1所示,每2根锚链分为一组,每组锚链系泊在平台4个垂直浮筒下缘外侧,STLP平台的主要参数如表2所示,为了计算系统整体参数,NREL-5MW风机的主要参数也一并给出。需要说明的是由于风机平台模型构造上的差异,风机系统整体关于质心的横摇、纵摇转动惯量与文献设定的不相同,其他参数与文献[6]中的设置保持一致。
此算例中以作用于浮式风机系统重心上的定常外力来模拟风载荷。模拟极端海况下平台运动实际上是模拟风机的生存条件,因此此时下风机处于关闭状态。为了简化模拟,一般海况下同样简化为关闭状态,只考虑定常风和波浪条件对于平台运动响应的影响。

表1 系泊系统主要参数Tab. 1 Main parameters of mooring system

表2 平台与NREL-5MW风机的主要参数Tab. 2 Main parameters of platform and NREL-5MW turbine

图4 计算网格Fig. 4 Calculation grids
为了保证数值模拟中可以准确生成波浪并稳定传播,捕捉流场内部变化、流场自由面变化等,需要对流场内部及结构物表面进行网格生成,并对部分区域进行网格加密。使用snappyHexMesh工具[18]生成网格,可以捕捉出物面边界条件,并加密背景网格,从而生成质量较高的网格。具体流程为:首先提取风机基础平台模型的特征边,并对自由面范围、平台表面进行网格加密,以便更精准地捕捉。计算网格如图4所示,STLP平台表面与附件的网格如图5、6所示。模拟中网格量约为260×104,为满足CFL条件,计算时间步长为0.005 s。

图5 水下平台表面网格Fig. 5 Grids on the surface of submerged platform
3 计算结果与分析
3.1 STLP自由衰减验证
通过对STLP单自由度自由衰减特性的模拟来验证naoe-FOAM-SJTU求解器的准确性和可靠性。平台的外形对称,故其纵荡周期等于横荡周期,横摇周期等于纵摇周期,模拟中只计算纵荡与纵摇周期。在计算STLP自由衰减特性中,风机叶片固定且无外部风浪载荷,在单自由度的条件下将STLP以某一设定初始速度值释放以观察平台的固有周期。
图7展示了不同自由度下平台自由衰减运动随时间变化的情况以及其振动能量的频域分布,STLP运动的固有周期可根据该时历曲线得到。CFD模拟(naoe-FOAM-SJTU)的固有周期结果与势流理论计算(BModes、FAST)的固有周期结果如表3所示,其中BModes为有限元模态分析结果,FAST为Han等[6]使用FAST(NREL设计的风机载荷分析软件)进行的全耦合时域模拟结果,以BModes为参考的模拟误差由下式计算:
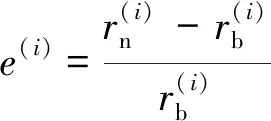
(9)

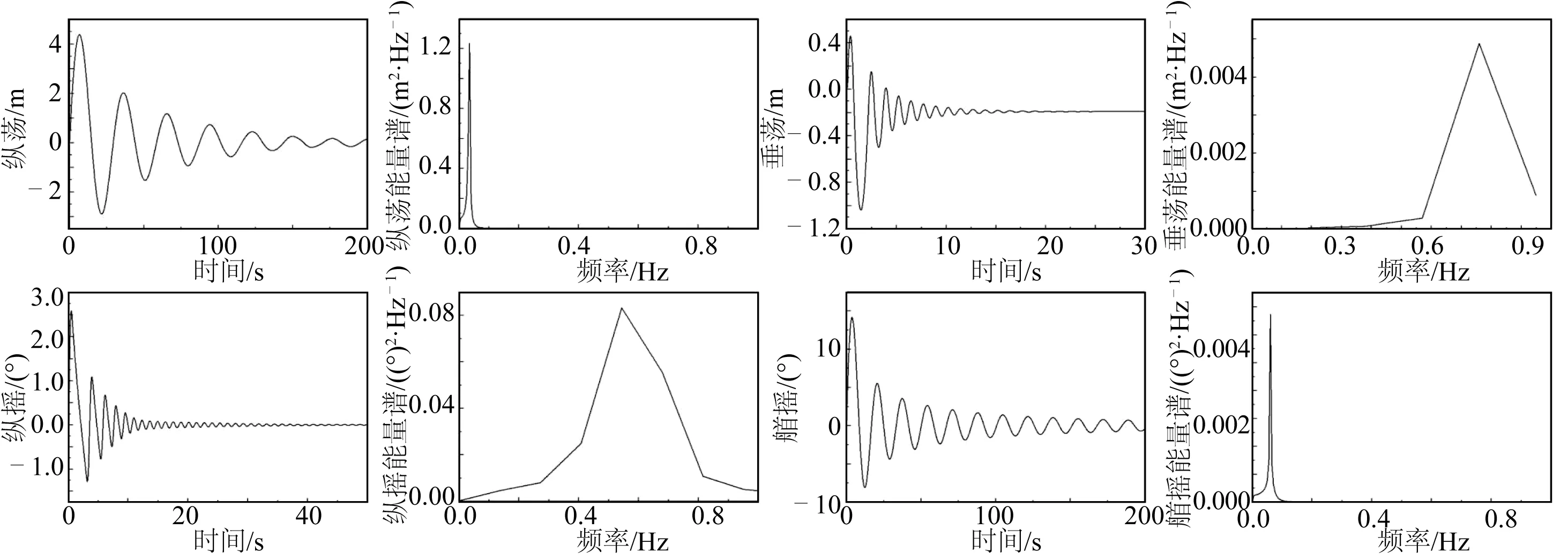
图7 STLP各自由度自由衰减运动时历曲线及能量谱结果Fig. 7 Time curves and energy spectrum results of free decay motion of the STLP

表3 STLP运动的固有周期Tab. 3 The natural period of motion of the STLP
由表3可知,使用naoe-FOAM-SJTU得到的模拟结果与已有文献结果吻合良好,误差均在3%以内(除纵摇(横摇)运动外)。其中纵摇(横摇)的自由衰减表现与文献结果偏差较大,这是因为本模拟中的风机模型与文献不同,因此对于纵摇(横摇)旋转轴的转动惯量与文献[6]中不同。该STLP的纵荡(横荡)的自有周期大于25 s,垂荡、纵摇(横摇)的自有周期小于3.5 s,完全符合浮式平台经验设计标准建议[19]。若平台的固有周期接近波浪频率,可能发生波浪载荷引起共振的危险。比较可知,相比于典型波浪频率,该STLP的纵摇(横摇)、垂荡运动的固有频率偏高,横荡(纵荡)、艏摇运动的固有频率偏低,所以共振危险较低,作为风机发电基础平台可以达到稳定输出的目的。模拟结果与文献结果吻合良好,证明了naoe-FOAM-SJTU求解器模拟此类问题的可靠性。
3.2 波浪场中STLP水动力运动响应结果
研究不同波浪场中平台的运动特性,初始时刻将平台自静止释放所有自由度运动,研究平台在波浪中运动的特性,绘制不同自由度运动、弯矩、系泊张力的时历曲线,并计算其振动能量的频域分布。最后将CFD模拟结果与已有结果对比。STLP结构与外界环境载荷都是对称的,因此文中只讨论纵荡、纵摇及垂荡运动响应。
3.2.1 极端海况下STLP水动力运动响应结果
此海况是平台的生存海况,风机处于关闭状态。将平台置于极端海况下,波浪谱采用Jonswap谱,有效波高14.4 m,谱峰周期13.3 s,平均风速49 m/s,将各自由度的运动响应结果进行统计,结果如表4所示。
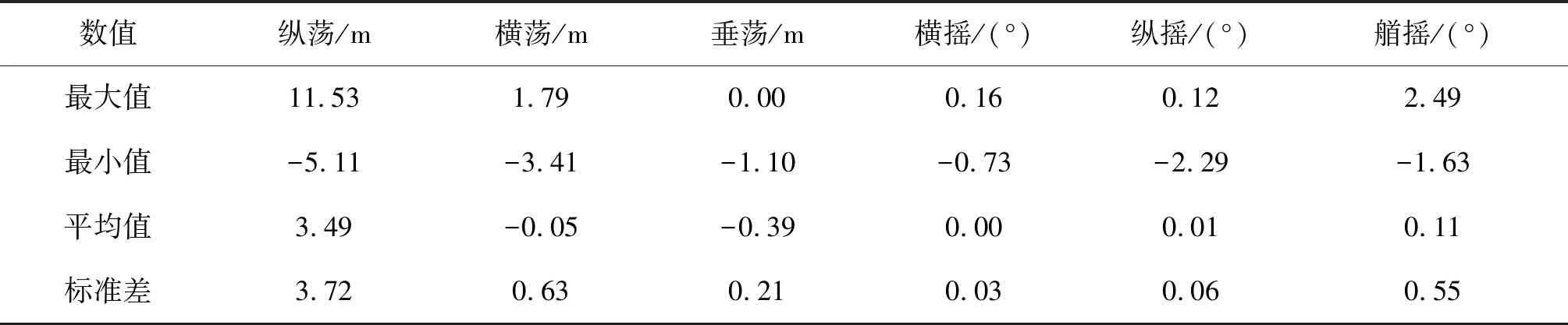
表4 极端海况下STLP运动响应统计值Tab. 4 STLP motion response statistics under extreme sea conditions
由于波浪及定常风力的联合作用,在6个自由度运动中,纵荡运动最显著,运动幅值最大,波动也最为剧烈。由于TLP平台的自身性质,平面外运动(横摇、纵摇及垂荡)的幅值很小;由于系泊系统、环境条件的对称性,横荡和艏摇运动的幅值也很小。将此海况下CFD结果与全耦合时域分析结果(考虑二阶波浪)的运动响应的平均值进行对比,如图8所示。
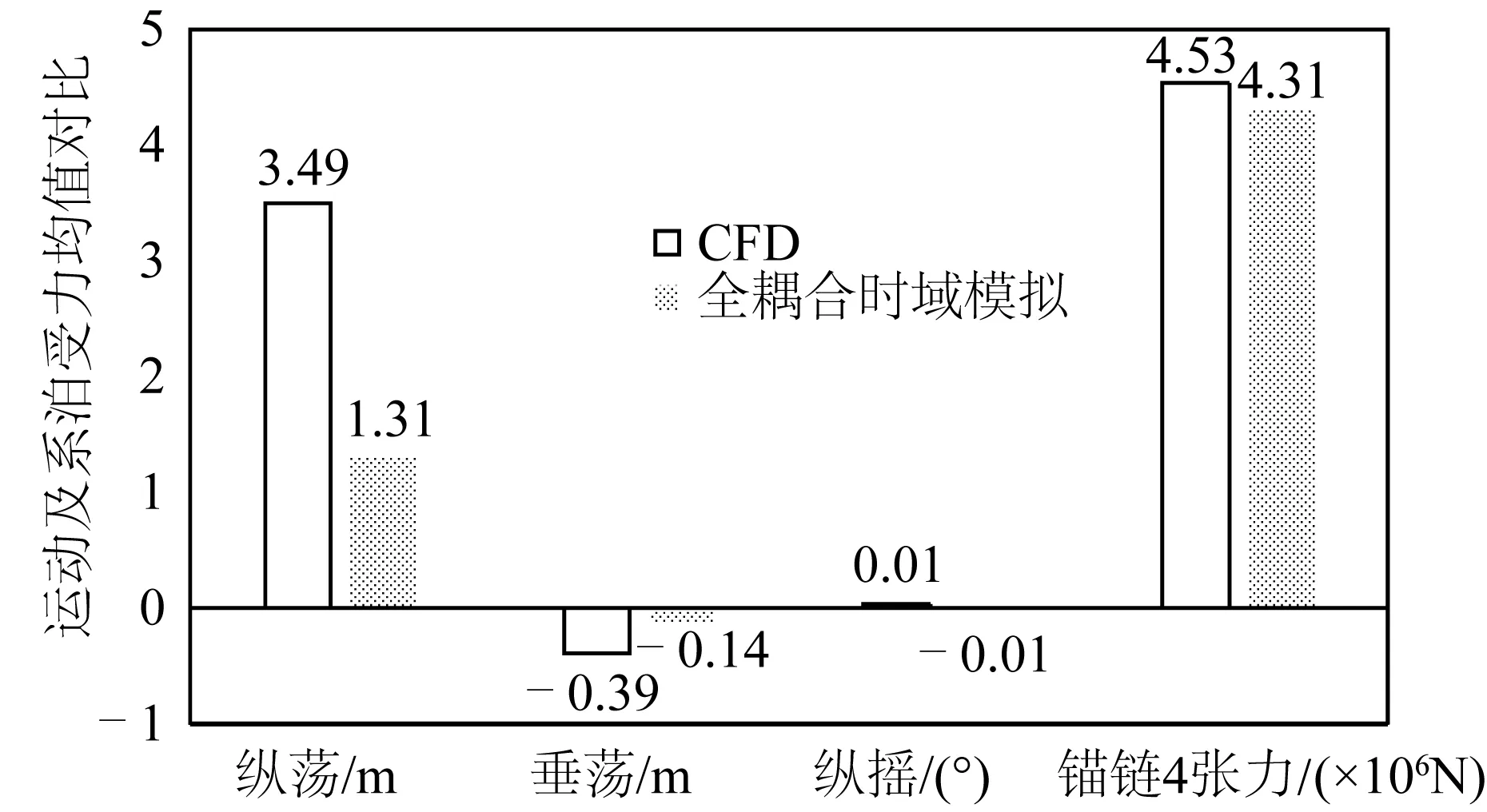
图8 极端海况下STLP的运动及系泊受力统计特性Fig. 8 Statistical characteristics of STLP motion and mooring tension under extreme sea conditions
由图8分析可知,使用CFD方法模拟极端海况下STLP的运动,相比于全耦合时域分析,运动幅度及系泊缆张力都偏大。这是更高阶波浪载荷作用在风机系统的影响所致。
将各系泊锚链的系泊力值进行统计,如表5所示,可见锚链3~6受到的平均张力最大,这是由于这4条锚链位于迎浪面。迎浪、背浪的锚链张力差距平均差值可达50 kN。

表5 系泊系统受力平均值Tab. 5 Average tension of the mooring system
将平台受到的波浪载荷、运动响应、所受弯矩和系泊系统受力的时历曲线进行快速傅里叶变换(FFT)处理,得到图9至图14。
图9为STLP在极端海况下的波浪载荷时历曲线与能量谱结果,可见CFD模拟考虑了波浪的各阶成分。图10为STLP在极端海况下的纵荡运动时历曲线与能量谱结果,此时在运动中波浪频率响应占主要成分,纵荡共振响应也较为明显。波浪频率响应成分远大于纵荡共振响应,虽然此时纵荡运动的固有频率(0.0336 Hz)接近波浪频率范围。这一特性与Han等[6]的全耦合时域分析结果相似。与全耦合时域分析结果对比可知,在CFD模拟中,高阶波浪成分更多,能量更分散,因此波浪频率成分峰值相比于全耦合模拟结果偏小,纵荡共振响应也更分散。这是因为图10(d)中最多只考虑到波浪二阶载荷,而图10(c)中波浪的各阶成分均考虑在内。对比可知,纵荡运动受到高阶波浪荷载的影响不敏感。
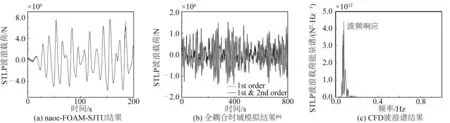
图9 极端海况下平台波浪载荷随时间变化曲线与能量谱结果Fig. 9 Time curves and energy spectrum results of wave load under extreme sea conditions
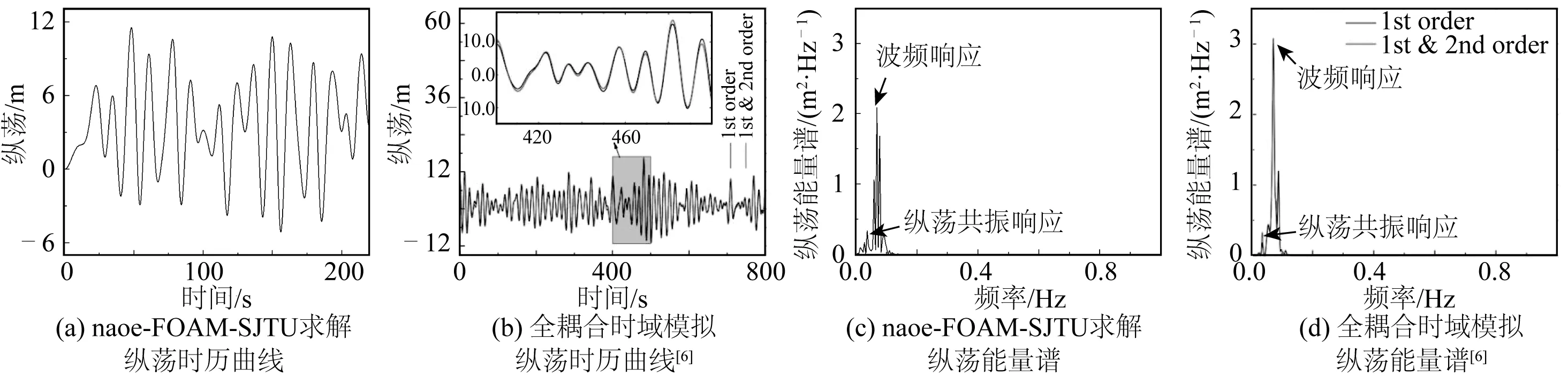
图10 极端海况下平台纵荡运动随时间变化曲线与能量谱结果Fig. 10 Time curves and energy spectrum results of surge motion of the STLP under extreme sea conditions
在纵荡运动随时间变化的曲线中,发现STLP平台的纵荡平衡位置不在0位置处,有明显漂移,这是定常风载荷的作用影响。CFD模拟中将湍流风场等效为定常风场,结果与全耦合模拟中的结果相差不大,可知在极端海况下,风机关停状态下风场对于STLP的纵荡运动影响不大。
图11为STLP在极端海况下的垂荡运动时历曲线与能量谱结果,可见在极端海况下,平台的垂荡运动响应中主要成分是波浪频率响应和纵荡共振响应,其中波浪频率为主导。因为平台初始为直立状态,垂荡会与纵荡在运动中发生耦合现象,因此能量谱中会出现纵荡共振成分。由于TLP系泊系统的固有特性,垂荡运动的平衡位置低于水平面。
极端海况、湍流风场中的STLP垂荡运动能量谱结果中(图11(d))明显可见风频率响应,但在CFD模拟中由于将风场等效为定常场,所以无此成分,说明极端海况下风场作用对于处于关停状态的风机STLP系统的垂荡运动影响较大。
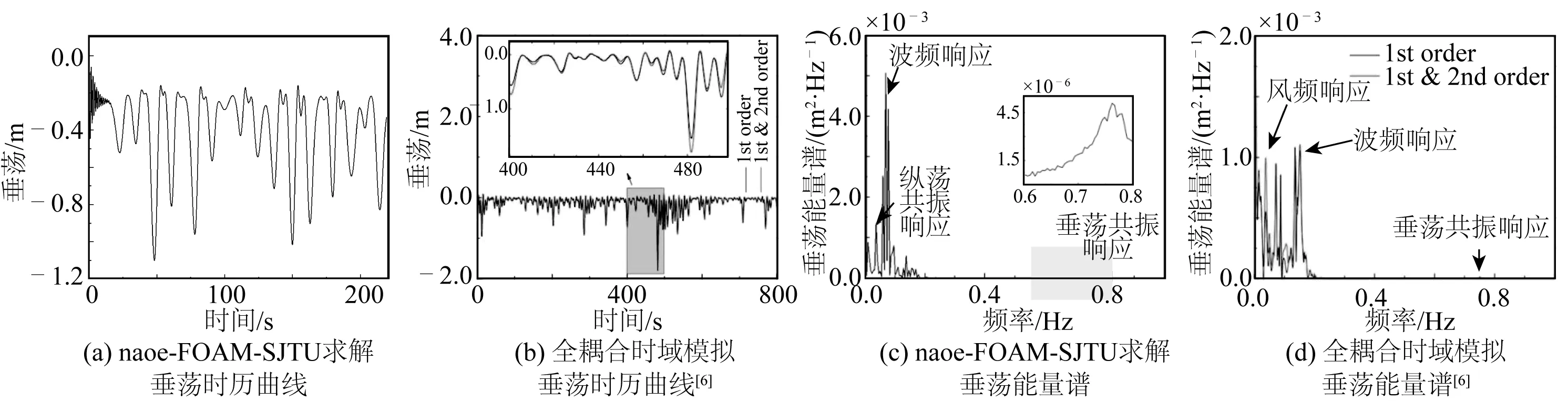
图11 极端海况下平台垂荡运动随时间变化曲线与能量谱结果Fig. 11 Time curves and energy spectrum results of heave motion of the STLP under extreme sea conditions
图12为STLP在极端海况下的纵摇运动随时间变化曲线及能量谱结果。在此情况下,能量谱中占主导成分的分别是波浪频率响应和纵摇共振响应成分。在CFD模拟中,除一阶、二阶波浪成分外,还可见更高阶的波浪成分,而全耦合时域模拟只有二阶波浪成分;由CFD结果可知,平台运动的纵摇共振响应成分由于波浪中的高阶成分的存在而变大,且响应的频率范围也更大。由上述分析可知,在此情况下波浪的高阶载荷对STLP的纵摇运动影响较大。与纵荡结果类似,风场对于极端海况下风机关闭状态下的STLP的纵摇运动影响不明显。
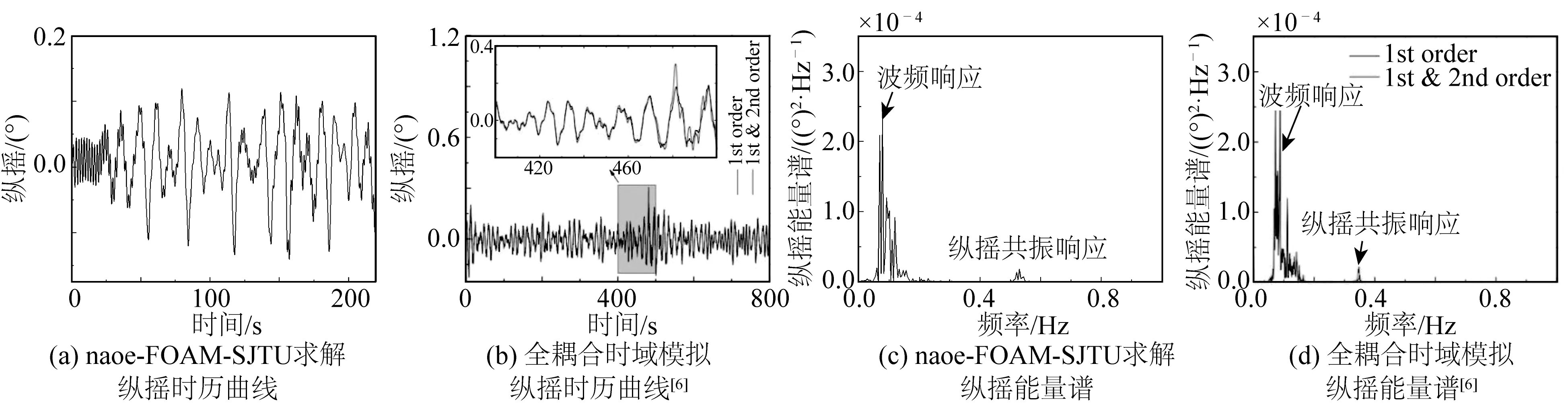
图12 极端海况下平台纵摇运动随时间变化曲线与能量谱结果Fig. 12 Time curves and energy spectrum results of pitch motion of the STLP under extreme sea conditions
由以上各图可知,平台在极端海况产生运动时,纵荡运动幅值较大,纵摇、垂荡运动幅值较小,平面内近似柔性,平面外近似于刚性。这种运动特性的产生是TLP自身的系泊特性决定的:TLP的张力腿平衡了大于重力的浮力,因此系泊缆始终是受拉状态,限制了平面外运动的幅值;STLP的主体是一个直立的浮筒,在吃水方向尺寸要远大于在水平面内的尺寸,所以受到的垂直方向波浪力要小于水平方向上的波浪力,因而在平面内具有柔性的特点[20]。STLP的这种特点使其可以很好地抵抗波浪引起的运动,并为风力发电提供一个相对稳定的环境。
图13是极端海况下平台受到的y向弯矩随时间变化曲线与能量谱结果,其中y向弯矩是针对风机基座而言的。由图可知在弯矩受力能量分布中,占主要成分的是波浪频率响应和平台的纵摇共振响应。将CFD结果与时域分析结果对比,发现CFD模拟中弯矩FFT结果的纵摇共振成分有显著升高,对应的频率范围也更广。出现这种现象是因为平台y向弯矩主要受纵摇运动影响,而CFD模拟中全面地考虑了波浪更高阶成分,高阶波浪载荷引起了更大的纵摇运动,使得风机的重力对于y向弯矩的贡献更大。

图13 极端海况下平台y向弯矩随时间变化曲线与能量谱结果Fig. 13 Time curves and energy spectrum results of y bending moment of the STLP under extreme sea conditions
锚链4位于迎浪面,图14为STLP在极端海况下锚链4的张力时历曲线及其能量谱结果。锚链4张力的能量谱中,占据主导地位的是波浪频率响应,且可见平台的纵摇、垂荡共振响应成分。而对比发现,全耦合结果中纵摇成分几乎不可见,说明高阶波浪载荷将引起系泊张力上更大的共振响应。

图14 极端海况下锚链4张力随时间变化曲线与能量谱结果Fig. 14 Time curves and energy spectrum results of #4 mooring tension of the STLP under extreme sea conditions
以上结果显示出:极端海况下STLP运动响应主要是波浪频率成分主导,也有共振响应成分存在,且高阶波浪载荷对于纵摇共振响应的增加效果较为显著,高阶波浪载荷将引起y向弯矩与系泊张力上更大的共振响应;风场对于极端海况下处于关停状态的风机垂荡运动响应影响较大;CFD结果与部分势流理论结果相比,可以明显体现出波浪中更高阶成分对于平台运动性能的影响,还可以可视化地显示出流场详细情况,如图15和图16所示。

图15 极端海况下瞬时流场Fig. 15 Instantaneous flow field under extreme sea conditions

图16 STLP在极端海况下不同时刻的流场状态Fig. 16 The state of the flow field at different times under extreme sea conditions
图15为极端海况下平台附近的瞬时流场,图15(a)为波谷经过平台,图15(b)为波峰经过第一排斜撑,图15(c)为波峰经过第二排斜撑。由图可以看出由于平台斜撑的存在,波浪在传播到斜撑时将被阻塞,产生局部次生波。当波峰到达斜撑时,在斜撑上产生了爬高现象。波浪继续传播,被斜撑阻塞的波浪离开斜撑,绕过斜撑继续传播,与入射波叠加,从而将导致波浪变形。
图16为极端海况下不同时刻的流场状态。可以看出,对于文中使用的二维不规则波,在经过一定时间的演化及与平台的相互作用后,流场变得非常复杂,整体波面受影响很大,已具有了三维特性。
3.2.2 中等海况下STLP水动力运动相应结果
将STLP置于中等海况下,波浪有效波高3 m,谱峰周期10 s,平均风速11.4 m/s,STLP运动响应统计值见表6。文中模拟只考虑风机基础平台的运动性能,暂不考虑与风场的耦合作用,因此关闭风机,使用作用在风机系统重心处的定常风来等效湍流风场。

表6 中等海况下STLP运动响应统计值Tab. 6 STLP motion response statistics under moderate sea conditions
与表4相比,由于环境较为缓和,中等海况统计值各项数据都比极端海况下的小很多。主要运动仍为纵荡运动。将各系泊缆所受张力的均值进行统计,如表7所示。

表7 系泊系统受力平均值Tab. 7 Average tension of the mooring system
由表7可知中等海况下各系泊缆绳的张力分布非常均匀。说明此时系泊系统可以充分发挥能力,比较不易发生断裂情况。
将平台受到的波浪载荷、运动响应、所受弯矩和系泊系统受力的时历曲线进行FFT处理,模拟结果如图17~22所示。
图17为STLP在中等海况下的波浪载荷时历曲线与能量谱结果,可见CFD模拟考虑了波浪的各阶成分。

图17 中等海况下平台受到的波浪载荷随时间变化曲线与能量谱结果(naoe-FOAM-SJTU)Fig. 17 Time curves and energy spectrum results of wave load under moderate sea conditions (naoe-FOAM-SJTU)
图18为STLP在中等海况下的纵荡运动时历曲线与能量谱结果,结果与极端海况下结果类似,主要成分为波浪频率响应,纵荡频率响应也较为明显。相比于图10中在极端海况下的结果,由于有效波高的降低,波浪频率成分减少,因此中等海况下纵荡共振响应更显著。
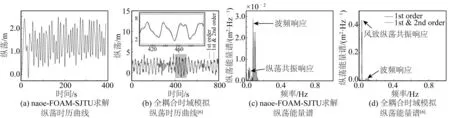
图18 中等海况下平台纵荡运动随时间变化曲线与能量谱结果Fig. 18 Time curves and energy spectrum results of surge motion of the STLP under moderate sea conditions
图19为 STLP在中等海况下的垂荡运动时历曲线与能量谱结果。发现在中等海况下,垂荡运动主要成分是波浪频率响应和垂荡共振响应,且可见纵荡共振响应,其中波浪频率响应最为明显。与图11对比可知,由于有效波高的减少,波浪频率成分减少,垂荡运动中的垂荡共振成分更加明显。与全耦合时域模拟结果对比可知,高阶波浪在中等海况下对垂荡共振运动的影响明显,使得垂荡共振运动对应的频率范围更大。
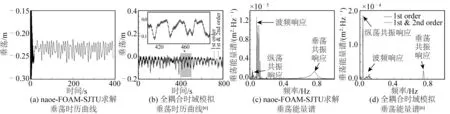
图19 中等海况下平台的垂荡运动随时间变化曲线与能量谱结果Fig. 19 Time curves and energy spectrum results of heave motion of the STLP under moderate sea conditions
图20为STLP在中等海况下的纵摇运动时历曲线及能量谱结果,与极端海况结果类似,纵摇运动的主要成分是波浪频率响应及纵摇共振响应,但与极端海况相比纵摇成分更显著。风机关停使得纵摇运动中几乎没有纵荡共振成分和垂荡共振成分,运动相对简单。
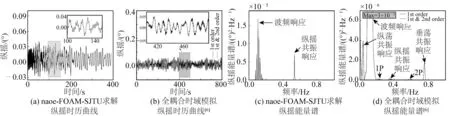
图20 中等海况下平台的纵摇运动随时间变化曲线与能量谱结果Fig. 20 Time curves and energy spectrum results of pitch motion of the STLP under moderate sea conditions
图21是STLP在中等海况下y向弯矩时历曲线与能量谱结果,其中主要成分为纵摇共振成分,同时可见波浪频率成分。相比于极端海况,由于纵摇成分的增加,中等海况下y向弯矩中纵摇成分显著增加。
图22为STLP在中等海况下锚链4的张力时历曲线及其FFT处理后的能量谱,其中能量谱主要成分为波浪频率响应、纵摇及垂荡运动频率成分,垂荡成分范围较大,这是因为系泊张力主要是由垂荡运动和纵摇运动决定的。

图21 中等海况下平台受到的y向弯矩随时间变化与能量谱结果Fig. 21 Time curves and energy spectrum results of y bending moment of the STLP under moderate sea conditions

图22 中等海况下平台的4号锚链张力随时间变化曲线与能量谱结果Fig. 22 Time curves and energy spectrum results of #4 mooring tension under moderate sea conditions
以上结果显示出风机关停状态下处于中等海况的STLP运动响应主要是波浪频率成分主导,也有共振响应成分存在,由于有效波高减小,相比于极端海况,各自由度运动的共振响应更加明显。高阶波浪在中等海况下对垂荡共振运动的影响明显,使得垂荡共振运动对应的频率范围更大。
由于不考虑风机作业的影响,CFD模拟的平台各自由度运动结果仍是波浪频率占主要成分。由于风场作用在叶片上的力沿纵荡方向,因此全耦合时域模拟结果中纵荡成分明显,对比说明在中等海况下作业中风机的影响决定了STLP的各自由度运动响应,考虑风机的作用影响则风机基础平台的运动更加复杂,对风机和基础平台的强度、抗疲劳性等性能的要求更高。
STLP在中等海况下的平台附近瞬时流场如图23所示,图23(a)为波峰经过第一排斜撑,图23(b)为波峰经过第二排斜撑;中等海况下不同时刻的流场如图24所示。

图23 STLP在中等海况下的平台附近瞬时流场Fig. 23 Instantaneous flow field near platform under moderate sea conditions

图24 STLP在中等海况下不同时刻的流场状态Fig. 24 The state of the flow field at different times under moderate sea conditions
由图23、24可知由于平台的存在,入射的二维不规则波浪在平台附近的传播受到了影响。平台斜撑具有阻塞作用,波浪在到达第一排斜撑时出现波面抬升,绕过斜撑后汇合,在第二排斜撑的阻塞作用下再次爬高,导致波峰线出现明显变形,不再为直线。
为了更清晰地分析波面,研究平台附近的流场及速度场。图25为T=375 s时平台附近流场及速度场,此时将平台隐去。可见由于平台斜撑的阻塞作用,波浪在斜撑附近辐射、绕射,形成了局部的次生波。分析速度场可知,平台斜撑的存在对于流体速度影响极大。

图25 T=375 s时平台附近流场及速度场Fig. 25 Flow field and velocity field near the platform at T=375 s
4 结 语
对一座STLP的运动特性进行了CFD数值模拟。首先对STLP的自由衰减运动进行了CFD模拟,计算出STLP的固有周期,并将结果与全耦合时域分析结果对比,发现二者基本吻合,验证了利用naoe-FOAM-SJTU求解器处理此类平台在波浪环境下运动问题的准确性和可靠性;在此基础上分别模拟了两种不同海况下平台的各自由度运动响应、风机对平台弯矩及系泊系统受力的时历特性及能量谱特性,并对结果进行了分析,得出以下结论:
1) 文中研究的TLP在波浪中的各自由度运动、风机对于底座的y向弯矩及系泊系统张力的主要成分是波浪频率响应及当前运动共振响应,除此之外,也耦合了其他自由度运动。
2) 极端海况下,平台的纵荡受波浪高阶成分的影响较小,纵摇比较容易受到高阶成分影响;中等海况下高阶波浪载荷对垂荡运动的影响明显。
3) 极端海况下风机处于关闭状态,风场对于STLP垂荡运动影响较大,对纵荡、纵摇影响很小;中等海况下风机的工作很大程度上决定了STLP的各自由度运动响应,考虑到风机的作用影响则风机基础平台的运动更加复杂,对风机和基础平台的强度、抗疲劳性等性能的要求更高。
4) 中等海况由于有效波高较小,因此相比于极端海况条件,波浪频率成分偏小,共振运动成分更显著。
5) CFD模拟结果相比部分势流理论结果更加精细,可以捕捉到波浪的高阶成分,并展示出流场可视化图像。由于结构物的存在产生了波浪的辐射、绕射现象,极端海况下流场非线性更强。
6) 文中研究的风机基础平台在平面内的运动呈现出柔性特点,在平面外的运动近似于刚性,具有良好的运动性能,可有效避免平台产生波浪频率上的共振,作为风机发电基础平台可以达到稳定输出的目的。
