聚焦波作用下立柱高阶波浪力特性研究

吕合媛，卢文月，李 欣

(上海交通大学 海洋工程国家重点实验室，上海 200240)

海洋环境千变万化，使得环境载荷十分复杂。随着近些年来海洋环境不断恶化，极端海况频繁出现，波浪砰击、高频共振响应(ringing)等现象成为了海洋工程领域内非常受关注的话题。在极端波浪作用下，由于波浪及其相互作用具有非线性特性，结构物上的波浪荷载由入射谱峰值频率附近的线性谐波分量和峰值频率倍数的高阶谐波分量组成[1]，这些现象具有很强的高频特性。海洋结构物多种多样，无疑都会遭遇恶劣海洋环境，即面对强非线性条件，结构物所遭受破坏程度也会因波浪情况的不同而不同。关于海洋中波浪载荷的理论分析工具能较好的预测波浪力的前两阶成分，但对于严峻海况下的高频成分预测结果与实际相差较大[2-3]。所以对总波浪力高阶成分的研究是非常需要且有意义的。

最初关于波浪高频特性的研究来源于对ringing现象的研究。ringing现象是多样化的，会出现在锚链、平台立柱、船体等部位，不断有学者对实际工程中出现的相关现象提出分析模型。挪威石油管理局(NPD)也曾汇编了一份文件总结挪威运营商和一家挪威工程公司对于高阶锚链响应分析的观点，Natvig[4]在其基础上进行深入的研究，提出新的分析模型，指出ringing产生过程中出现的非高斯波可能是诱发其产生的一重要因素。Davies等[5]对陡波作用下的模型和实尺度固定结构物和浮动张力腿平台的ringing现象及其载荷特性进行了总结。Grue等[6]也通过不同尺度下的试验研究，总结了各波浪参数对波浪力的影响，详细解释了高频谐波成分出现的原因。Chaplin等[7]通过重复试验，分析了作用于同一陡波的垂直圆柱在固定和底部由弹簧支撑两种状态下的试验结果，得出了结构物的瞬态剧烈响应来源于波浪的高阶成分的结论。另有相关试验证实ringing现象就是高阶谐波对结构物瞬态剧烈响应的激发，且通常是三阶和频分量[2, 6]。

极端波浪的激励和响应等特性一直以来都是海上工程领域备受关注的话题，为了充分捕捉结构物在极端波浪中的总力和响应，必须分离并精确计算高阶波载荷谐波，由此众多学者开始展开一系列对于波浪高频特性的研究。关于提取规则波高阶谐波的研究多是利用傅里叶变换，但对于不规则波，傅里叶变换显然不再适用[1]。Ma等[8]应用平均小波能量来分析谐波下波浪力的幅值，展开波浪水槽中垂直圆柱在聚焦波作用下的试验，用平均波能分析了聚焦位置处确定频率范围内力和波高的前六阶谐波分量，结合波能分析对六阶分量进行对比研究，结果表明，该方法适用于瞬态或短时时空序列的谐波分析。Zang等[9]提出了一种适用于陡波作用下圆柱所受载荷分析的新方法，通过假设自由表面高度和聚焦波水平载荷在频率和波陡上均存在广义斯托克斯谐波序列，提取相互作用中较高的谐波，将一波群与其逆波群分别作用得到的力的时历相结合，来提取总水动力载荷中的完整谐波结构，并通过垂直圆柱波浪试验证明了此方法的优越性。此方法被称作“逆相位分解方法”，后面也将利用此方法展开研究。

1 聚焦波理论模型

Chaplin[10]总结了实验室内通过聚焦手段生成瞬态波的三种优化方式，分别为相速度法、逆传播法和波群速法，对于聚焦波的模拟，普遍采用相位聚焦法，在物理水池或数值水池中使波浪能量在特定的地点与时刻汇聚，生成能量高度集中的强非线性波浪。由于不同波频或波数的前进波在水中传播时存在传播速度不同的色散现象，在聚焦波的模拟中，需要使波浪能量定点汇聚，使各成分波在某一位置同时达到最大值，叠加形成聚焦波列。随机波浪可以表示为无数个随机余弦波浪的线性叠加：

(1)

其中，N为组成波数目，an、kn、ωn、εn分别为第n个组成波的波幅、波数、圆频率和随机相位，为了使所有组成波在特定位置xc及特定时刻tc同时达到最大值，随机相位εn可以设为εn=knxc-ωntc。这样，波浪的分布可以描述为:

(2)

采用新波理论推演聚焦波群来模拟海洋环境中的极端波浪。Tromans等[11]提出了能够模拟给定波峰值的瞬态波“新波”理论。该理论用来模拟给定目标波峰高度的聚焦波，优点为不受组成波数目的影响，通过实现设定的目标波峰高度，并将波浪谱能量按照相关比例分配到不同的频率区间内，进而求得各组成波波幅的高度，无论组成波数目多少，在目标位置处聚焦波波浪的波峰值均为事先指定值，且该方法不需要很长的随机波列[12-13]。新波理论模型是将波面看做一个高斯随机过程，把历史记录中最不利的波面情况通过数学方法表达出来。单位波峰的标准型波面可以表达为波面升高的自相关函数形式，即：

(3)

式中：δω为能量谱的频率间隔，S(ωn)是组成波对应的波浪谱，σ2是波浪谱S(ωn)的方差。通过ηN(t)=ηNΔr(t)可以获得与给定波峰值一致的瞬态波波浪升高的时历表达。波峰波谷的不对称性依赖于所选取波浪谱的形态。每个组成波的波幅值按照下述公式求解：

(4)

则单向入射波聚焦模型可以表示为：

(5)

图1 局部波浪参数描述Fig. 1 Description of local wave parameters

聚焦波是一种瞬时大波，属于非平稳过程，采用局部波浪参数对其进行描述。如图1所示，聚焦波的波峰值Hc为静水面到最大波峰高度的垂向距离；波谷Ht为峰前波谷到静水面的距离；波峰前后波谷之前的时间间距为聚焦波的谷谷周期Ttt，上升周期和下降周期分别为波面从峰前波谷到波峰、从波峰到峰后波谷的时间，聚焦波的理论局部波数k和局部波长L均通过谷谷周期计算得到，波陡定义为波峰与谷谷周期的比值Hc/Ttt；KR为散射参数,定义为立柱等效半径R与波长L的比值；KC数定义为πA/R。

2 数值模型及准确性验证

2.1 模型参数

数值计算波浪水池模型如图2所示，水池长10 m，高1.25 m，初始自由液面水深为0.9 m，自由液面以上高度为0.35 m，在距离水池入口5 m处放置虚拟浪高仪，水池尾端1.5 m为“消波区域”，结构物放置于水池5 m处。数值计算假设流体不可压缩、黏性系数为常数，控制方程为连续性方程、N-S方程和自由液面控制方程。数值波浪水池入口端边界条件设为速度入口，另一端出口设为压力出口，底部与立柱表面设为壁面(无滑移)，水池两侧面设为对称面。

图2 数值波浪水池Fig. 2 Numerical wave tank

参照真实海洋平台所处海域情况设计工况，采用波浪参数为有效波高Hs=13.4 m，谱峰周期Tp=14.7 s，峰高因子γ=2.4的JONSWAP谱，并以200的缩尺比进行换算。结构物参照真实海洋平台立柱以200的缩尺比换算得来，为一个横断截面为正方形的立柱，表1给出了结构物的具体尺寸。

表1 结构物尺寸Tab. 1 Size of structure

选择STARCCM+软件中的VOF波模块造聚焦波，是一种纯数值造波技术，需要在波浪入口处导入各个成分波浪的参数，包括每个成分波的波幅、周期和相位信息。成分波的参数参照之前所述方法计算得来。数值水池“消波区域”通过在边界施加控制方程，整个流域按照此方程进行控制。

为了得到效率与质量较高的数值模拟计算，进行数值计算之前需要进行网格和时间步长的敏感性分析。经验证，在纯波浪作用下，水池宽度对波浪的计算没有影响，为提高计算效率，波浪校核阶段建立“伪二维”数值波浪水池，即将水池宽度设置为很小量(y方向)，这里设置为0.001 m。在数值波浪水池中，从自由液面附近到整个计算域进行了五次网格密度的过渡，表2给出了网格划分的区域位置，以及每块区域内网格的尺寸为基准值的百分比。分别设置基础尺寸为0.003 m、0.006 m、0.009 m、0.012 m、0.015 m来测试网格的敏感性，由图3可以看出基础尺寸越小计算精度越高，0.003 m、0.006 m的网格计算精度均较高且相差不大，考虑到0.006 m的基础网格计算时间短于0.003 m,所以最终选择0.006 m的网格进行计算。

表2 网格划分方案Tab. 2 Mash scheme

图3 不同基础尺寸下模拟对比Fig. 3 Simulation comparison under different foundation sizes

2.2 波浪校核

利用新波理论推演出一系列单向入射的聚焦波群，聚焦位置为距离入口5 m处，聚焦时间为5 s，波幅为1的标准聚焦波型，选择0.02 m，0.04 m，0.06 m，0.07 m作为波峰值来制定工况，表3为工况参数。

表3 工况参数Tab. 3 Parameters of cases

尤其是以聚焦波为代表的极端波浪的传播过程是非线性的，在聚焦目标位置处，各组成波的相位和幅值与目标值不可避免会存在差别。为了提高聚焦波的模拟质量，采用相位—幅值优化方法对波浪信号进行优化。通过比较聚焦目标位置测量谱与目标谱的差距，调整波浪输入信号的相位及幅值信息[14]。迭代优化过程如下：

φi+1=φi+(φT-φMi)

(6)

(7)

其中，φi为初始输入的波浪信号或上一次输入的波浪信号的相位角，φi+1为新的信号相位角，φT为目标波浪时历组成波成分的相位角，φMi为试验得到的波浪时历组成波的相位角，a为波浪组成成分的幅值，其上下标具有与φ相同的含义，迭代优化过程中均是多退少补的过程，尽管在迭代优化过程中高阶波浪成分均作为自由组成波处理，但是由于每次优化都是基于上一次模拟结果进行，因而相位—幅值优化方法内在的考虑了波浪非线性效应。

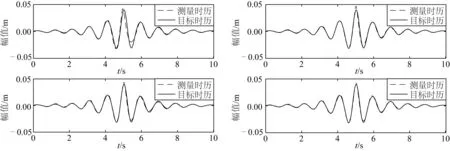
图4 工况2优化结果Fig. 4 Optimization results of NO.2 work conditions

图5 工况2优化后模拟波浪谱与波浪靶谱对比 Fig. 5 Comparison diagram of simulated wave spectrum and wave target spectrum after optimization of NO.2 work conditions

作为示例，图4为工况2的优化过程，图5为工况2优化后模拟波浪谱与波浪靶谱对比。

图6为各个工况波浪优化结果，图6(a)为设定4个工况的优化结果，图6(b)为设定工况所对应增加180°相位角的波列优化结果。从中可以看出相位—幅值优化方法使得聚焦波最终模拟结果与目标时历更为接近，优化效果较好。0.02 m，0.04 m，0.06 m校核结果相比0.07 m效果较好，原因为波幅为0.07 m工况波陡较大，会出现波浪破碎现象，校波过程较为困难。

图6 工况1～4优化结果Fig. 6 Optimization results NO.1～NO.4 work conditions

2.3 模型准确性验证

将数值水池宽度扩大至1 m与模型试验波浪水槽一致。计算立柱的三种固定方式在聚焦波作用下所受波浪力，三种固定方式分别为：完全固定、单自由度纵荡、单自由度垂荡。立柱的运动设置通过在模拟树中添加DFBI模块，在此模块中选择所涉及的运动方式来完成。数值计算涉及网格运动，应用重叠网格法进行建模。重叠网格部分的网格参数按照自由液面附近网格尺寸设置，初始化后，重叠网格与数值水池网格交界处会自动过渡处理，图7为算例初始化后三维网格模型。

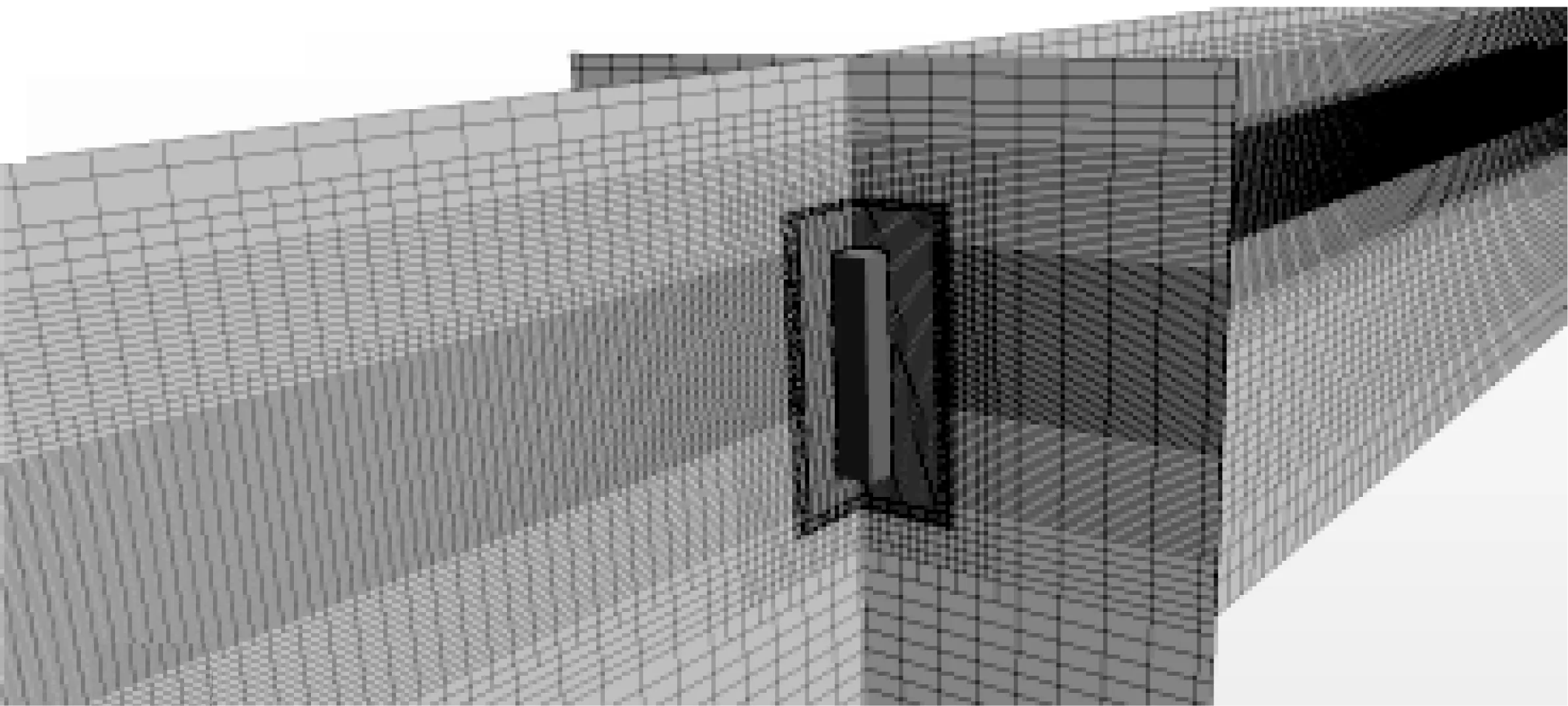
图7 三维网格模型Fig. 7 Three-dimensional mesh model

选择工况2进行模型准确性验证，图8为固定立柱在物理试验与数值模拟下所受纵向与垂向波浪力对比，图9为单自由度垂荡运动状态下物理试验与数值模拟中立柱所受纵向与垂向波浪力及垂荡运动对比。可以看出各结果的整体趋势一致，但数值有略微差别，分析此差别是由校波结果与试验环境引起的，可以得出此数值计算模型具有准确性。

图8 固定立柱在物理试验与数值模拟下所受x与z方向波浪力对比Fig. 8 Comparison of wave forces in x and z directions on fixed columns in physical test and numerical simulation

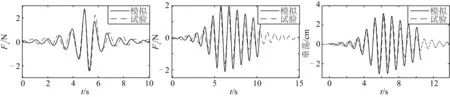
图9 垂荡运动状态下物理试验与数值模拟中所受x与z方向波浪力及垂荡运动对比Fig. 9 Comparison of wave forces in x and z directions and heave motion under heave motion condition in physical test and numerical simulation

3 结果分析

3.1 逆相位分解法

逆相位反演法是基于斯托克斯理论呈现的一种通过改变波群相位并对时历结果进行线性组合来分离高阶波浪力的方法[1]。根据经典的斯托克斯波理论，结构物水平水动力载荷为:

F=A1f11cosφ+A2(f20+f22cos2φ)+A3(f31cosφ+f33cosφ)+A4(f42cosφ+f44cosφ)

(8)

其中，Ai为波浪力中第i阶幅值，系数fmn代表波浪与波浪力之间的传递函数,φ=ωt+φ0为入射波成分的相位。逆相位分解法分离波浪力中奇次谐波和偶次谐波，对于给定的波浪条件，需要两个来自相差180°相位角的反向入射波时历。对于初始选择的信号，会生成一列在聚焦位置出现波峰的波浪时历,因此反向信号会生成一列在聚焦位置出现波谷的波浪时历。此时的水动力载荷为：

Fπ=A1f11cos (φ+π)+A2[f20+f22cos2(φ+π)]+A3[f31cos (φ+π)+f33cos (φ+π)]+

A4[f42cos (φ+π)+f44cos (φ+π)]

(9)

对两列时历进行基本运算可以得到：

(10)

(11)

即可将波浪力中奇偶次成分分离。

3.2 波浪力分离处理

对数值模拟得到的波浪力时历按照逆相位分解法进行处理，首先对对应两列时历进行峰值位置核对，来消除时间上的偏差引起的误差，然后按照上述方法将对应两列数据加和处理得到偶次谐频波浪力，差减处理得到奇次谐频波浪力，最后分别还原各阶波浪力对应的时历。图10～21为工况1、2纵向与垂向波浪力、高频分离结果以及各阶波浪力时历(图中e为实际波浪力，1为一阶波浪力，2为二阶波浪力，3为三阶波浪力，4为四阶波浪力)。工况3、4的结果不再进行展示。

图10 工况1，固定状态下Fx、高频分离结果及各阶波浪力时历Fig. 10 NO.1, Fx, high-frequency separation results and wave force of each order in a fixed state

图11 工况1，固定状态下Fz、高频分离结果及各阶波浪力时历Fig. 11 NO.1, Fz, high-frequency separation results and wave force of each order in a fixed state

图12 工况1，单自由度纵荡运动下Fx、高频分离结果及各阶波浪力时历Fig. 12 NO.1, Fx, high-frequency separation result and wave force of each order under single freedom of surge motion

图13 工况1，单自由度纵荡运动状态下Fz、高频分离结果及各阶波浪力时历Fig. 13 NO.1, Fz, high-frequency separation result and wave force of each order under single freedom of surge motion

图14 工况1，单自由度垂荡运动状态下Fx、高频分离结果及各阶波浪力时历Fig. 14 NO.1, Fx, high-frequency separation result and wave forces of each order under single freedom of heave motion

图15 工况1，单自由度垂荡运动状态下Fz、高频分离结果及各阶波浪力时历Fig. 15 NO.1, Fz, high-frequency separation result and wave forces of each order under single freedom of heave motion

图16 工况2，固定状态下Fx、高频分离结果及各阶波浪力时历Fig. 16 NO.2, Fx, high-frequency separation results and wave force of each order in a fixed state

图17 工况2，固定状态下Fz、高频分离结果及各阶波浪力时历Fig. 17 NO.2, Fz, high-frequency separation results and wave force of each order in a fixed state

图18 工况2，单自由度纵荡运动状态下Fx、高频分离结果及各阶波浪力时历Fig. 18 NO.2, Fx, high-frequency separation result and wave force of each order under single freedom of surge motion

图19 工况2，单自由度纵荡运动状态下Fz、高频分离结果及各阶波浪力时历Fig. 19 NO.2, Fz, high-frequency separation result and wave force of each order under single freedom of surge motion

图20 工况2，单自由度垂荡运动状态下Fx、高频分离结果及各阶波浪力时历Fig. 20 NO.2, Fx, high-frequency separation result and wave forces of each order under single freedom of heave motion

图21 工况2，单自由度垂荡运动状态下Fz、高频分离结果及各阶波浪力时历Fig. 21 NO.2, Fz, high-frequency separation result and wave forces of each order under single freedom of heave motion

由以上波浪力结果显示此次数值模拟计算较为稳定，且每组对应波列作用下的波浪力结果有良好的对称性。工况4为所有工况中最陡的一个，波浪优化结果较差于其他工况，其波浪力结果相比于前三个工况较为不稳定，两列波浪力对称性略差，可以推断波浪优化校核结果对波浪力结果有一定的影响，也可以认识到对于较陡波浪情况下数值模拟的计算不易控制，对于较陡波浪数值模拟的准确性有待继续考究。

由高频分离结果可以发现奇次成分中一阶以上成分相较于一阶成分非常小，在奇阶次图中几乎难以发现，偶阶次图中可以清晰分辨出二阶及更高阶成分，则说明高阶成分相比于一阶成分为非常小量。同时可以发现二阶成分前仍有一段频率较低的成分存在，这是由于逆相位分解法推演过程中二阶成分中含有和频与差频成分(式(11))，图中频率较低部分为差频成分[12]。

纵观数据处理结果，各工况下单自由度纵荡运动状态下各阶波浪力均小于固定状态，且高阶力明显较小；单自由度垂荡运动状态下纵向波浪力与固定状态相差甚微，而垂向各阶波浪力明显高于固定状态，且高阶成分突出。

由各阶波浪力时历图可以观察到，高阶波浪力时历主要集中分布在波浪聚焦发生前后，越接近聚焦时间，波浪力越大，并且从工况1至工况4，高阶成分逐渐变得明显突出，说明高阶波浪力大小与波浪自身的条件有关，能量越集中的地方就更易出现高阶成分，高阶波浪力的出现使得波浪力峰值更为尖锐，这会导致结构物受力变大、增速较大，结构物受力过于突然有可能会导致非常严重的后果。

3.3 各阶波浪力统计值

图22 各阶波浪力平均值统计Fig. 22 Statistics of the average values of wave forces of each order

图中可以看出一般情况下波浪力阶次越高平均值越小，偶尔会出现高阶波浪力大于低阶波浪力的情况。

图22(a)、(c)、(e)为各状态下各阶纵向波浪力平均值统计，对于纵向波浪力，固定状态下各阶值均为最大；其次是单自由度垂荡运动状态，此状态一阶波浪力与固定状态下相差甚小，但高阶力明显小于固定状态；单自由度纵荡运动状态下各阶均值最小，且高阶力有明显的下降趋势。可以得出固定结构物承受的纵向载荷更为严重；结构物的纵向运动会一定程度上削减纵向各阶波浪力成分，且高阶成分明显减小；结构物的垂荡运动对纵向波浪力一阶成分影响较小，高阶成分明显减小。

图22(b)、(d)、(f)为各状态下各阶垂向波浪力平均值统计，对于垂向波浪力，单自由度垂荡运动状态下各阶均值最大；其次是固定状态；单自由度纵荡运动下各阶均值最小，且高阶力有明显的下降趋势。聚焦波在工况4波幅为0.07 m，第二节波浪校核时效果较差，出现过波浪破碎现象，此时呈现出该工况下各阶波浪力不稳定。可以得出结构物的纵荡运动可以一定程度上削减垂向各阶波浪力成分，垂荡运动反而增加了垂向各阶波浪力成分。

整体看来单自由度纵荡运动对纵向与垂向各阶波浪力均有缓和作用，且纵向波浪力各阶成分有明显减小；而单自由度垂荡运动对纵向各阶波浪力影响较小，对垂向各阶波浪力产生了加剧作用，且高阶分量有明显增加，进一步增加了垂向波浪力。

4 结 语

基于立柱在聚焦波作用下的数值计算，讲述了一种利用改变波浪信号来分离垂直立柱所受高阶力的方法。介绍了聚焦波的模拟与分离高阶波浪力的具体理论方法，以STARCCM+软件为工具，分别计算了立柱在固定、单自由度纵荡和单自由度垂荡三种运动状态下所受波浪力，详细讲述了高阶波浪力分离方法的应用。经系统的研究，得出以下结论：

1) 波浪较稳定的状态下，数值模拟也有较好的稳定性，每组对应波列作用下的波浪力有良好的对称性。

2) 聚焦波模拟优化过程中利用相位—幅值优化法，在波浪稳定的状态下，取得了良好的优化结果，但对于波陡较大、波浪状态严峻的情况，数值模拟与物理试验经对比更易于破碎，优化过程难以实现，导致与目标值相差较大。

3) 逆相位分解方法可以有效分离波浪力的高阶成分。

4) 文中分别计算了结构物三种状态下所受波浪力，不同运动状态下立柱所受波浪力有显著不同。整体看来，固定结构物承受的纵向波浪载荷最严重，单自由度垂荡运动结构物承受的垂向波浪载荷最严重；单自由度纵荡运动对纵向与垂向各阶波浪力均有缓和作用，且纵向波浪力各阶成分有明显减小；而单自由度垂荡运动对纵向各阶波浪力影响较小，对垂向各阶波浪力产生了加剧作用，且高阶分量有明显增加，进一步增加了垂向波浪力。

研究过程中不难发现，数值计算在模拟真实波浪时仍存在一些不足，对于较难问题仍需继续研究，来提高数值计算的准确性。