基于尾流模型的风场偏航控制优化研究

宁 旭，曹留帅，万德成

(上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室 船海计算水动力学研究中心(CMHL)，上海 200240)

随着风能技术日益成熟，风机的单机发电功率和风电场规模都在迅速增大[1]。目前投入使用最多的风力发电机类型为水平轴风机(horizontal axis wind turbine)，该类风机在工作中会不可避免地在其盘面后方形成尾流区域，该区域内的风速较低且湍流强度很高，这使得位于下游尾流区域中风机的发电量下降，疲劳载荷显著增加，这就是所谓的尾流损失。目前，大多数运营中的风电场控制仍然遵循单机最大功率追踪策略，即每台风机作为独立的个体，根据来流速度调整叶轮转速以达到风速—功率曲线上的设计值[2]。这导致迎风向的前排风机虽以较优状态工作却会对下游风机形成严重的尾流效应，由此可带来高达40%以上的电能产出损失[3]。为了进一步提高风电场的性能和使用年限，针对风场优化控制的算法开发逐渐成为该领域的研究热点。

风洞试验[4-5]和计算流体动力学(CFD)模拟[6-8]可得到高精度的风场数据，但高昂的设备成本和计算代价使其不能有效地解决优化问题，而尾流模型基于基本物理原则对尾流场进行合理的简化，能够通过显式函数迅速地得到尾流场的速度分布，其精度虽略逊于物理试验和数值模拟，但可满足风场控制的实时性要求，在工业界已得到广泛应用。Bastankhah等[9-10]通过简化雷诺平均(RANS)方程推导出偏航角度与风机尾流偏移的关系式，这为发展偏航控制算法提供了有力的理论基础。目前大多研究将尾流模型用于风场布置优化[11-14]，事实上，风场布置会受到地形、交通、布缆等因素的限制，故相关研究成果有较大的局限性，而通过控制风机工作参数(如转速、偏航角等)的方式提高风场效率并降低荷载的可行性已被相关试验和数值研究所证实[15-16]。其中，利用风机偏航使尾流在下游偏移以减轻尾流损失的做法称为偏航控制(yaw control)或尾流操纵(wake steering)[17]。Fleming等[18-19]通过实地测试验证了偏航控制策略的有效性，Quick等[20]考虑了风向测量误差等不确定因素，提高了偏航控制的可靠性，Howland等[21]也通过实际风场测试证实了偏航控制对于提高总体功率和发电稳定性的意义，但是这种策略在不同风况以及不同风场布置形式下的性能差异仍未得到有效分析，由于这种控制优化算法可应用于已建成的风电场，深入考察该策略在不同条件下的效能有重要意义。

基于尾流模型构建大型风电场尾流求解和总功率预测模块，结合粒子群优化(particle swarm optimization，简称PSO)算法寻求多种风况下不同布置形式风电场的偏航优化控制方案，以此减少尾流损失，实现风场电能产出的优化。此外，还研究了这种优化策略在不同条件下优化效果的优劣，为未来的风电场总体优化控制研究提供参考。

1 风场尾流分布及总功率

1.1 尾流模型

尾流模型是通过基本的物理原则(如动量守恒等)或简化流动方程的手段，建立的风机工作状态与尾流速度分布的显式关系式。文中所采用的尾流模型由Bastankhah等[10]提出。该模型的基本原理是通过简化RANS方程得到速度损失通量及横向速度通量在流向的守恒关系，可表达如下：

(1)

(2)

图1为风机尾流速度分布，根据图1所示，工作中的风机圆盘后方会形成一个低速核心区，该区域内风速的大小和方向可看作均匀分布，随着尾流向下游发展，由于核心区与周围未受阻滞的流动之间存在速度差，其边界处会形成剪切层并不断向内部发展，核心区不断收缩，直至剪切层在尾流中心处汇聚，该处便是近尾流区和远尾流区的分界点。物理和数值试验表明[9]，远尾流区的时均速度损失在x和y方向均符合高斯分布形式，即：

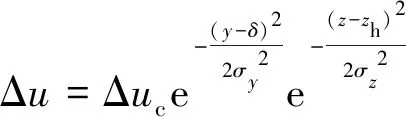
(3)

式中：速度损失Δu=(u-u)/u，u为来流速度；下标c代表尾流核心区；zh是轮毂高度；σy和σz分别为横向和垂向的高斯特征长度，与尾流宽度呈正比；δ为尾流在横向的偏移量。核心区速度损失可由下式计算：

(4)

式中：γ是风机偏航角，CT是风机的推力系数，D为风轮直径。在大气湍流强度下，可以假设尾流宽度随流向距离线性增加，即：

(5)

(6)

其中，x0是近远尾流区分界点处的流向坐标；ky，kz为横向和垂向上尾流宽度的膨胀率，对于陆上风场该值可取0.075，对于海上风场该值介于0.04与0.05之间[22]。

图1 风机尾流速度分布示意Fig. 1 Sketch of velocity distribution of wind turbine wake

1.2 尾流叠加

风场内部的风机往往会受到上游多个风机的影响，为了计算多尾流的相互作用，首先根据风向对风场建立直角坐标系，其x轴与风向平行，据此可以确定每个风机上下游位置的次序，坐标系原点设于第一台风机处。每个风机盘面都被划分为具有一定分辨率的二维网格平面，并定位出所有盘面内部的网格中心点如图2所示。在每个网格点上，可以根据上游风机Ti的相对位置由公式(3)计算出其产生的尾流速度损失Δui，不同风机尾流混合所造成的速度损失以平方叠加法则计算，即：

(7)

式中：Δutot为所有上游风机引起的总体速度损失。

1.3 确定风机气动系数

风机的推力和功率可由推力系数CT和功率系数CP表示为如下形式：

(8)

(9)

其中，ρ=1.225 kg/m3为空气密度；A是风轮面积；ue为等效入流速度，是计算风机气动性能的重要参数，有多种计算方法。文中将ue定义为风轮盘面内所有网格点速度的平均值[23]，即：

ue=u

(10)

其中，Δui为第i个网格点处的总体速度损失，N为风轮盘面内的网格点总数。理论上在风机型号确定的情况下，风机的气动系数CT及CP是等效入流速度ue的函数：

CT=fT(ue),Cp=fP(ue)

(11)

但该函数通常不能由解析式直接表达，故使用线性插值法获取。文中选用NREL-5MW标准风机[24]，该风机轮毂高度zh=90 m，叶轮直径D=126 m，额定转速与入流风速分别为12.1 r/min及11.4 m/s，额定功率5.3 MW，其CT—ue和CP—ue曲线见图3。

2 粒子群优化算法

2.1 粒子群优化算法流程

粒子群优化(PSO)算法[25]模仿鸟群觅食的行为，鸟抽象为粒子而食物就是目标函数的最优解。PSO算法由若干具有随机位置和速度的粒子进行初始化，随后每个粒子以计算过程中其本身的最优点pb和全局最优点pg为参考，在参数空间中往复运动以寻找最优解，其计算流程如图4所示。

图3 NREL-5MW风机气动系数曲线Fig. 3 Aerodynamic coefficients curve of NREL-5MW wind turbine

图4 粒子群算法流程Fig. 4 Flowchart of particle swarm algorithm

在风场优化问题中，风机的偏航角度γ是优化参数，目标函数值为风场总功率输出，所以第i个粒子的位置和适应值分别表示为：

pi=(γ0, …… ,γk, …… ,γNt)

(12)

(13)

式中：k为风机编号，Nt为风机数量。其速度v和位置p更新公式如下：

(14)

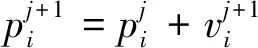
(15)

式中：j为循环数；w为惯性权重，文中取0.4，控制粒子对上一个循环中速度的继承量；c1、c2为学习因子，分别决定每个粒子自我总结和向群体中领导者学习的能力，通常取c1=c2=2；r1，r2为0至1之间的随机数，总粒子数为Np。需要注意的是，文中所使用的尾流模型只在-30<γ<30范围内适用，所以需要对更新后的粒子位置检查和纠正使其满足上述条件，当粒子越过边界时将其赋值为边界值。

2.2 算法收敛性验证

偏航优化问题的参数维度高，且求解域内存在多个极值点，而粒子群算法具有一定随机性，传统的相对误差收敛性判据可能使程序提前终止导致寻优效果较差。为了选择适当的算法总粒子数和迭代次数，以下文中图5所示风场为例，入流风速、风向和湍流强度分别设为7 m/s，270°和5%，风机行间距Δr与列间距Δc均为4D，针对粒子数和迭代次数进行算法收敛性分析。

图6中显示了粒子总数分别为10，20，30和40时，粒子群算法每次迭代得到的风场总功率结果。图像显示，在4种情况中粒子群均可以在10次迭代以内将总功率从11 864 kW提升至13 500 kW以上，粒子数较高时收敛速度略快，随着迭代次数增加，粒子数为10和20的计算最终分别只停留在13 767 kW和14 093 kW，陷入了局部最优，粒子数增大至30和40时搜索得到的最优解可达到约14 200 kW。需要指出的是，粒子群算法属于随机搜索算法，在收敛前并非每一次迭代都能够提高目标函数值，且最终结果仅为近似全局最优而非理论最优解。经验表明，越接近最优解时，越需要更多的迭代次数才能进一步提高优化结果，粒子数为30和40时在迭代30次后收敛于同一水平，可认为已接近最优解，因此在下文的研究中将粒子总数和迭代次数均设置为30。

图5 风场布置示意Fig. 5 Sketch of wind farm layout

图6 不同粒子数下的寻优结果Fig. 6 Optimization results with different total particle numbers

3 算例分析

为了探究偏航控制策略在不同风况和不同风场布置间距下的可行性和有效性，设置了两座具有不同间距的风场，采用典型的平行四边形布置，30台风机以5行6列平行均匀分布，行列间的夹角通常根据当地盛行风况确定，文中设置为75°，风场风向标与具体布置形式如图5所示。共设置了6组不同工况，在不同风速、风向以及湍流强度的风况条件下，对偏航控制的优化效果进行了对比分析，各工况参数列于表1。

表1 各工况参数设置Tab. 1 Parameter setup of different cases

3.1 风向与风速

入流风速对风机的气动性能及尾流特征有显著影响，在机组布置确定的情况下，风向的改变决定了各风机在流向上的间距大小，进而成为评估风场所受尾流损失程度的关键参数。为了分析不同风速风向条件下偏航控制对风场发电量的优化情况，对工况1和2的优化结果进行了对比，见表2和表3。

在工况中，优化前所有风机均为迎风状态，即偏航角度为0，优化后根据粒子群算法得到的最优解，将不同位置的风机调整至合适的偏航角度，使尾流轨迹偏移以达到优化风场的目的。表2中列出了工况1采用偏航优化策略前后风场总功率的数据。据表可以看到，风场的总功率对风向非常敏感，如在270°和255°风向下后者总功率是前者的2.5倍，这是由于270°的风向刚好与风机组成行方向平行(见图5)，此时后排风机会被前面同行的风机尾流完全遮蔽，这样叠加后的尾流速度损失将远高于其他风向的情况导致风场发电量损失严重，同理，195°风向与风机成列方向平行，故总体发电量亦远低于其他风向。因此，在不同风向上偏航控制对风场性能提高的程度有着巨大差异，在270°和195°风向的情况下，优化的效果最为显著，风场总功率分别提高了14.60%和8.78%，因为偏航控制可使尾流偏移至轮毂中心线两侧，此时可有效改善对下游风机的遮蔽效应。此外，在风向为150°和135°时，虽然优化率较低，但仍能使总功率得到可观的改善，分别提高了3 575.0 kW和2 848.8 kW。而在其他风向上，优化前风场总功率已均超过120 MW(无尾流干扰下的理想总功率为159 MW)，说明风场所受尾流损失已经很小，故偏航控制在此时无法大幅提高风场性能。

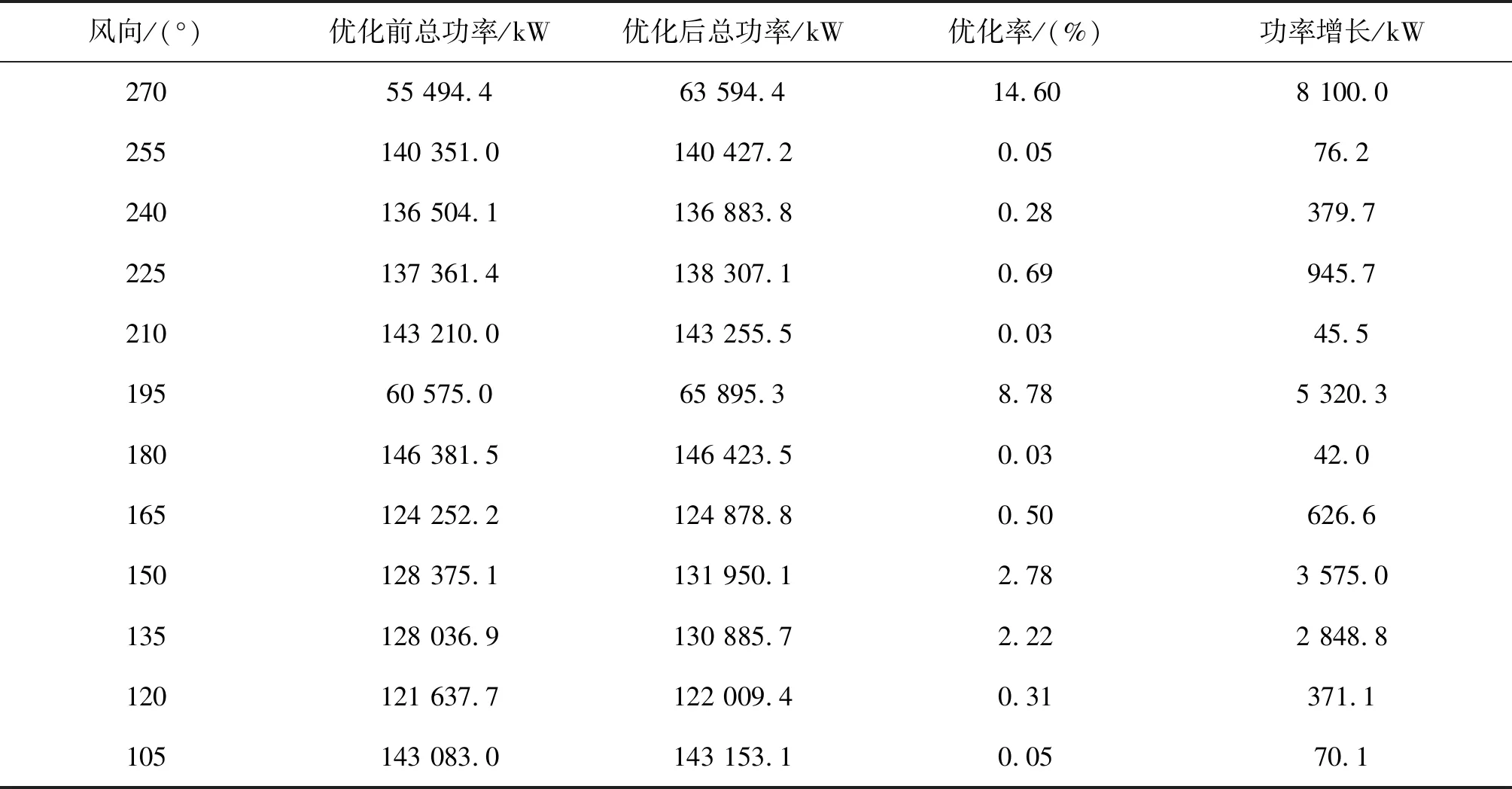
表2 工况1优化结果Tab. 2 Optimization result of case 1

表3 工况2优化结果Tab. 3 Optimization result of case 2

工况2与1相比，入流风速由额定风速11.4 m/s降至7.0 m/s，风机的叶尖速比由7.0升至7.9，推力系数增加，尾流损失加剧，下游风机发电量损失随之增大。表3的数据显示，此条件下对风机进行偏航控制可以实现更高的优化率，在270°和195°两个风向上，总发电量分别提高了19.78%和13.49%。

以270°风向条件为例，工况1与2分别以图7中的偏航角度对风场实施了偏航控制。优化前后的尾流场速度损失分布如图8所示，由图8(a)、(c)可知，优化前所有风机以0°偏航角迎风且为串列布置，下游风机位于上游风机尾流的正中央，这使得风场尾流损失非常严重，尤其在入流风速为7.0 m/s时，风机推力系数增大，首排风机后的速度损失已经接近0.8；由图8(b)、(d)可知，通过调整每台风机到合适的偏航状态，其尾流分别向南北产生了明显的偏移，虽然这样会使自身功率降低至原来的cos3γ倍，但可大幅降低其下游机组所受的尾流影响，实现风场的整体优化。由图8可见，在优化后的风场中，风机后方速度损失由接近0.8降至0.5～0.6之间。

图7 270°风向各风机偏航角度Fig. 7 Yaw angles of each wind turbine under 270°wind direction

图8 270°风向尾流场速度损失分布Fig. 8 Wind farm wake velocity deficit distribution under 270°wind direction

图9为采用偏航优化控制前后各风机功率的对比情况 ，结果显示在不利风速下，无论风速大小，若不对风机进行偏航调整，则仅有首排风机能够获得可观的发电量，下游风机在尾流的影响下入流速度有限，工作效率非常低；经过偏航优化，下游风机发电量均得到一定提升，尾流损失得到明显改善，电能产出更为均匀。由于风机尾流内部不仅速度降低，湍流强度也会明显上升，使得受其影响的风机入流稳定性下降，会对风机叶根、低速轴等结构产生更大的疲劳载荷，所以偏航控制不仅能够提高整体发电量，还有益于降低机组疲劳载荷，提高其服役时长。

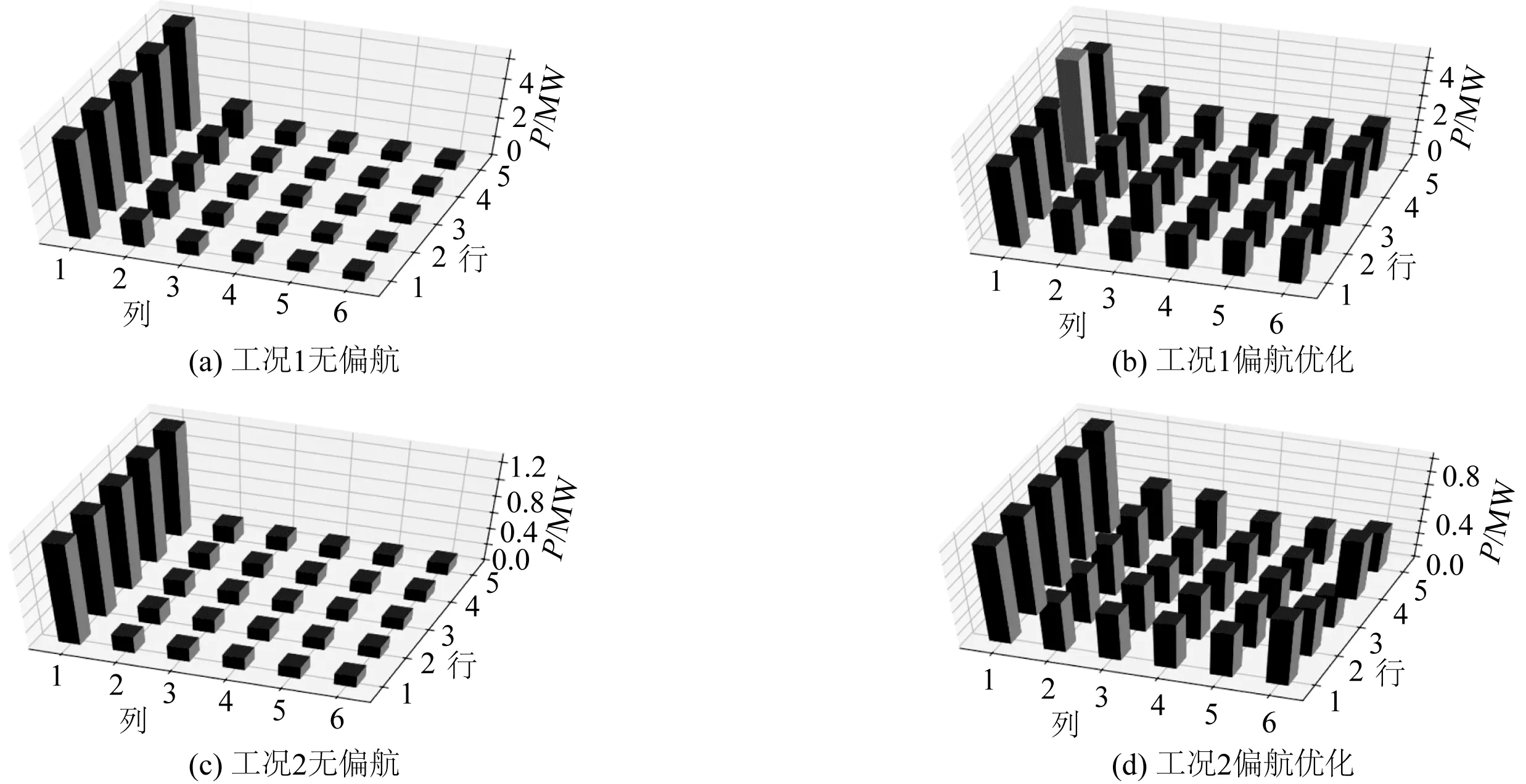
图9 270°风向各风机功率分布Fig. 9 Power outputs of each wind turbine under 270°wind direction

3.2 不同湍流强度

湍流强度定义为流向脉动速度标准差σu与平均来流风速u之比：

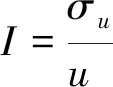
(16)

大气的湍流强度对风机尾流的发展起着至关重要的作用，更大的湍流强度会加速大气环境与尾流区域的动量交换，风机叶尖后侧形成的剪切层会以更快的速度增长，远尾流区的开端提前，尾流膨胀速度加快。工况1和2中湍流强度为5%，该值与海面上中性或稳定大气边界层内部的情况接近，而在陆上风场中，由于地面粗糙度的提高，边界层底部摩擦加剧，边界层内湍流更为活跃，尤其在光照充足的白天，大气转变为对流边界层，此时风机工作高度上的湍流强度往往超过10%甚至更高。为了探究在这种情况下偏航控制的性能，将工况3中的湍流强度设置为15%，并在风向为270°的条件下与工况1和2的结果进行对比。

图10为工况3和4中风机的最优偏航角度，比工况1和2有所降低。在湍流强度较低时，尾流速度恢复慢，同样偏航角度下，尾流轨迹相对非偏航的中心线偏离更远，所以大偏航角可以明显提高下游风机的有效入流速度；反之，湍流强度很高时，速度损失恢复速度提高，尾流偏离程度对偏航角的敏感度下降，此时偏航角过大反而会造成总功率下降。从图8(b)、(d)与图11的对比中可以看出，湍流强度提升至15%后，风机尾流的横向尺度更大，同样偏航角下尾流的偏移程度明显减弱。

图10 270°风向各风机偏航角度Fig. 10 Yaw angles of each wind turbine under 270° wind direction

图11 偏航优化后尾流速度损失分布Fig. 11 Wake velocity deficit distribution of wind farm with yaw control

表4为270°来流下，湍流强度分别为5%和15%时的风场发电量及偏航控制的优化效果对比。结果显示，风速相同的情况下，湍流强度增大10%使得未优化前的功率提升约30%，而此时偏航控制所能带来的发电功率增长非常有限，在来流为11.4 m/s和7.0 m/s时的优化率分别跌至仅1.36%和4.00%。

表4 不同湍流强度下偏航控制效果对比Tab. 4 Comparison of effects of yaw control under different turbulent intensities

3.3 不同风机间距

风机的布置间距对风场的年发电量影响非常显著，加大风机在主风向的布置间距可以有效降低尾流损失，但由于受到空间限制，电缆、运输和运维成本的约束，风场布置往往要通过合适的布置间距来找到发电量和成本间的平衡[21]。对于以平行四边形布置的风场而言，7个风轮直径的间距更为常见，比如丹麦的Horns Rev风电场[26]，故将讨论风场布置间距为4D和7D时偏航控制效果的变化。

图12显示了工况5和6的偏航优化控制方案，与工况1和2相比，拉大布置间距后各风机偏航角度变化很大。在间距为4D时，除最后一列风机以外，大部分风机产生了±30°的偏航角(该尾流模型所能够计算的最大偏航角)，实际上进一步增大偏航可能会有更好的优化效果；而当间距增大至7D时，尤其在低风速下，最优偏航角度基本在20°以内，同一行风机的偏航角度根据流向位置逐渐变化，这是因为更长的间距使得尾流速度损失得以更好的恢复，偏离尾流能够带来的收益明显减小。

图12 各风机偏航角度Fig. 12 Yaw angles of each wind turbine

图13中将偏航优化前后的各风机功率绘制成折线图，对比发现在两种入流风速下偏航策略有所不同：在额定风速下第一列风机基本以额定功率运转，而第二列或第三列的风机以较大角度偏航以提高下游的总体功率；在低风速下，首列风机进行偏航，其下游各列风机的功率均得到提升。

图13 偏航优化前后各风机功率曲线Fig. 13 Power outputs of each wind turbine with and without yaw control

工况5和6与工况1和2的结果对比列于表5，以观察加大间距后的偏航控制效能。间距增大后，虽然偏航控制仍能为风场发电能力带来一定的提升，但在来流为11.4 m/s和7.0 m/s时的优化率仅有1.04%和1.94%，由于尾流损失减小，偏航优化控制的效果显著下降。

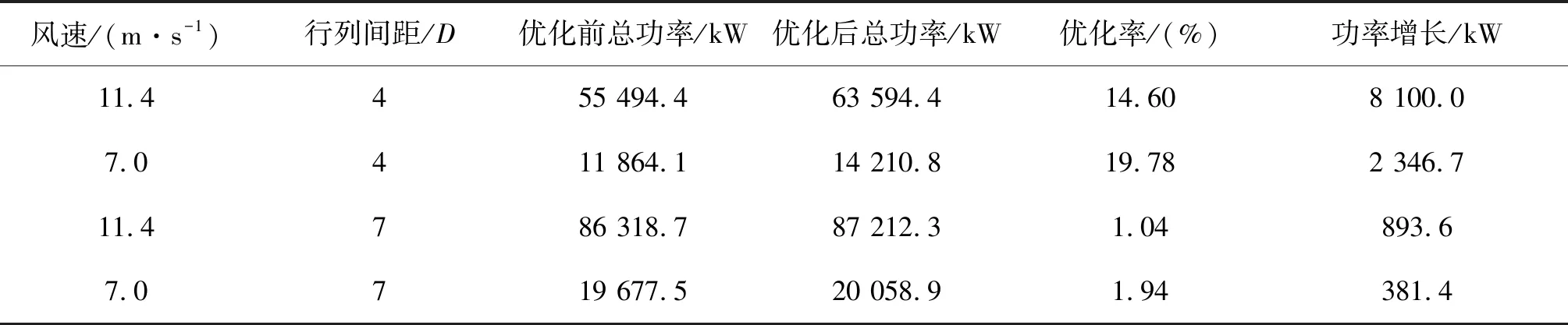
表5 不同布置间距下偏航控制效果对比Tab. 5 Comparison of effects of yaw control under different wind turbine spacings

4 结 语

基于偏航尾流模型结合粒子群优化(PSO)算法对不同风向、风速、湍流强度以及风场布置间距情况下的偏航优化效果进行了对比研究。结果显示，偏航控制可以在不利风向下(即风机排列与来流平行时)发挥明显效果。由30个NREL-5MW风机以5行6列间距4D均匀布置的平行四边形风场，面对湍流强度为5%的11.4 m/s额定风速，风向为270°和195°的情况下，偏航可使风场总功率分别提升14.6%和8.78%，尤其在风速为7.0 m/s时，能分别提升总功率的19.78%和13.49%。而在湍流强度提升至15%后，各风况下的偏航效果均降至5%以内，这是由于湍流的增强使得尾流的横向尺度增大，且尾流偏转效应不再明显。风场布置间距由4D增大至7D后，尾流损失可以在更长的距离内得以更好地恢复，偏航控制能带来的收益也明显地降低。综上，风机偏航控制能够在大气条件较稳定，不利风向且风机的流向间距较小时显著提升整体发电量，风速降低优化率更高，但在湍流强度高且风机间距较大时，偏航控制的效能非常有限，考虑到实际大气测量的不确定性以及计算误差，此类条件下不宜采用偏航控制优化策略。