序贯截尾检验法在一维修正增程弹密集度评估中的应用

舒延春

(92941部队43分队，辽宁 葫芦岛125001)

密集度是炮射一维修正增程弹最重要的战术技术指标，其相对于传统无修正弹药的最大优势是成倍提高了纵向密集度[1]。通常衡量地面火炮弹药密集度大小的指标包括两个，即纵向密集度和横向密集度，分别由EX/X和EZ表示，其中EX和EZ分别为纵向和横向散布中间误差，X是最大射程。一维修正增程弹是一种新概念的灵巧弹药，其经济成本远高于普通弹药，因此，传统的密集度指标评估方法势必造成试验成本的增加；目前针对这类弹药常用的检测方法为序贯截尾检验法，该方法能够在不增加使用风险的前提下，减小试验鉴定样本量，科学评定一维修正增程弹的密集度指标。

1 传统检验法

传统检验弹药落点密集度指标的方法是点估计法，该方法根据落点坐标计算其纵向概率偏差和横向概率偏差，假设：进行N组试验条件一致的修正弹密集度试验，每组发射n0发弹丸，并用(ΔXij，ΔZij)表示第i组第j发弹弹丸的纵向横向偏差，其中i=1，2，…，N，j=1，2，…，n0。N组数据就构成了一个数据样本。

下面以计算纵向概率偏差为例，给出点估计法的具体应用。

N组射击后，落点纵向偏差的均值为

(1)

落点纵向偏差的方差最大似然估计为

(2)

纵向概率偏差为

(3)

用点估计计算落点概率偏差，该方法通常在舰炮发射的弹药中使用。根据数理统计理论，假设样本是服从正态分布的随机变量，且通过抽样得到一定的样本，然后进行方差的计算和评价。所以，采用此方法评定密集度，需要有足够的样本来保证估值的置信度和精度[2]。表1和表2中的数据为试验组数N、每组试验射击次数n0与点估计系统误差δm和均方差误差δp的关系。

由表1和表2可以看出，样本数越多，估值精越高。为保证点估计的精度，取N=6、n0=6比较合适，此时，可以保证系统误差和均方差误差接近0.1。也就是说，从统计结果来说样本容量为36，并不算多，但对修正弹来说，如果外场射击试验一个项目进行36发试验存在较大难度；从理论上讲，射击试验次数越多，试验周期越长，难以保证试验条件的一致，将导致各子样不是同一母体，估值失真，试验经费也太高。所以，这种传统的试验评定方法不适合对精度要求较高的修正弹药落点密集度的评定。修正弹必须采用新方法进行密集度评定。

表1 点估计系统误差δm

表2 均方差误差δp的关系

2 序贯截尾检验理论算法

目前一些行业比较常用的样本检验方法是序贯检验方法，其优点是可以确定平均试验次数，缺点是所确定值与试验结果通常不相等。所以在应用序贯检验法时，首要任务是试验次数上限值的确定，若试验次数小于该值时做出决策，则试验结束，节省试验次数；若试验次数达到上限时，不可再进行试验，此时必须做出决策，这种方法被称为序贯截尾检验方法[3]。

设随机变量X(射程)的概率函数为f(x，θ)，建立互相竞择的检验假设。

H0：θ=θ0，H1：θ=θ1=λθ0>θ

式中：θ为分布参数；λ为鉴别比，且λ>1。

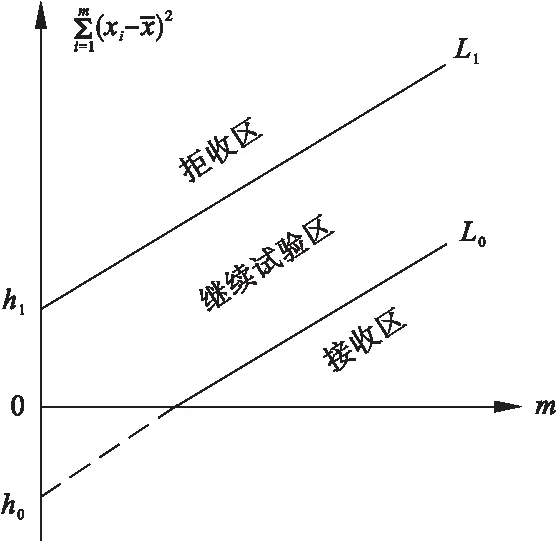
设α和β分别为弃真错误和采伪错误的概率，如果有两个与α和β相关的常数，假设为A和B，这两个数的大小关系为：0

根据子样数据似然比

(4)

进行判别，其原则为：

如果B

如果Om≥A，则拒绝假设H0，终止试验；

如果Om≤B，则采纳假设H0，试验结束。

所以，在进行检验时是序贯的，每次试验都要进行假设检验的判断，并作出是否进行下一次试验以及采纳或拒绝H0的结论。

针对修正增程弹落点密集度试验样本，落点偏差(x，z)为服从正态分布的独立随机变量，即X～N(μx，σx)，Z～N(μz，σz)，其中μx、μz、σx和σz均未知。

以纵向密集度检验过程说明序贯检验方法的应用。

第一步：对试验样本标准方差σ的互相竞择检验假设进行建立。

H0：σ=σ0，H1：σ=σ1=λθ0>σ0

式中：σ0为研制指标要求的纵向标准偏差；σ1为使用方能接受的最大纵向标准偏差指标。

第二步：以风险相当原则为依据进行α和β，的选择，二者分别为研制方和使用方的风险率，一般由双方协定，然后即可由公式(5)、(6)计算A和B的值。

(5)

(6)

且A和B应满足关系式0

第三步：判别

经过m次密集度试验，得到纵向子样(x1，x2，…，xm)。

当假设H0：σ=σ0为真时，出现子样(x1，x2，…，xm)的概率为

(7)

当假设H1：σ=σ1为真时，出现子样(x1，x2，…，xm)的概率为

(8)

因此，当

(9)

继续进行第m+1次试验；当

(10)

采纳假设H0，试验结束；当

(11)

拒绝假设H0，试验结束。

(12)

(13)

(14)

式(12)～(14)中，μx为未知的总体均值，在样本量足够时，对于总体均值可用子样(x1，x2，…，xm)的均值代替，所以子样均值为

(15)

等式右端的m用(m-1)替代，变形为

(16)

继续进行第m+1次试验；当

(17)

采纳假设H0，试验结束；当

(18)

拒绝统计假设H0，试验结束。

图1 序贯检验图

图2 序贯截尾检验图

图1中，L0和L1的斜率为

(19)

截距h0和h1绝对值相等，h0为

(20)

第四步：序贯截尾检验的判定

由H0：θ=θ0，H1：θ=θ1=λθ0>θ0的假设检验，当α和β均给定时，进行n0次发试验后，可应用式(18)～(20)进行检验。若检验结果还需进行试验，但序贯检验又必须在n0处截尾，则检验方法如下：

如果式(22)成立，则采纳假设H0。

(22)

当满足下式时，拒绝假设H0。

(23)

式中C为拒绝上/下限，

(24)

3 应用计算

以一维修正增程弹最大射程纵向密集度序贯检验为例[4]。假设已知参数：对于修正弹，其最大射程纵向密集度指标为纵向概率偏差Ez=89m；将纵向概率偏差换算成可接收的标准偏差σ0=Ez/0.6745=132m；

建立互相竞择的检验假设

H0：σ=σ0=132m，H1：σ=σ1=λσ0，

使用蒙特卡洛法进行计算，对λ、α和β三个参数取不同数据，计算双方实际风险α′、β′和平均试验次数n0，结果如表3所示。

确定序贯截尾检验方案：在表3的15个方案中，可选取1个较为合理的进行检验。如：选择方案7，选定鉴别比λ=1.3，双方风险α=β=0.2，截尾数n0=20，但实际弃真概率和采伪概率分别为α′=0.1312，β′=0.2003。

表3 序贯检验方案

开始试验，以方案7为例利用检验表法进行序贯检验。

(25)

(26)

式中：xm为对应于第m发的落点纵向偏差；Am为对应于第m发的接收区域边界值；Rm为对应于第m发拒收区域边界值。

建立修正弹纵向密集度序贯检验表[5]，并将试验数据和结论记录于检验表内。以一次纵向密集度试验为例，表4为该次密集度试验序贯截检验表。

表4 密集度试验序贯截尾检验表

由表4可知，

当试验进行到第13发时，按照序贯截尾检验规则，试验结束，认为纵向密集度满足要求。

4 结束语

按序贯检验理论，和传统的经验做法比较，在满足生产方风险和使用方风险可接受的情况下，可以减少高价值弹药试验样本量，降低试验费用，缩短试验周期。尤其是对于一维增程修正弹这种成本和试验条件一致性较高的新概念弹药，在研制阶段采用本文提出的序贯截尾检验法对其密集度进行评估十分有效，同时该方法的结论还可以为靶场性能状态鉴定阶段提供借鉴。