现冲突激兴趣绘流程导实践

陈元炎

摘 要：“烙饼问题”主要探讨的是优化时间的策略问题，在教学如何烙3张饼时，教师应着重引导学生探究怎样用数学的方法来解决实践操作中的时间优化。通过数学计算与惯性思维影响下实际操作之间所需时间的差异冲突，引导学生绘制操作流程表;通过观察、修正、优化、丰富流程表，轻松破解实践中的思维惯性。并在流程表的引导下轻松参与操作，在做、说、看、听的多元协同作用下，激发学习兴趣，进行有效学习。

关键词：“烙饼问题”;流程表;优化时间;学习兴趣

新课程标准对学生情感态度的要求包括：积极参与数学活动，对数学有好奇心和求知欲。[1]兴趣是最好的老师，是学生学习的内部动力，知识的传授只是学生学习的外部因素。可是，在课堂教学实例中，普遍存在“一切以知识的掌握为核心”的教学设计理念，让学生成为知识的接收器，使学习成为学生沉重的负担。数学学习应重视在数学活动中的感悟与联想，埋下数学思想的种子，为深入学习数学做好准备。

一、“烙饼问题”教学设计的不足之处

（一）重知识的传授   轻兴趣与联想

在众多课例中，教师都重视学生的预习，让学生不断去经历烙饼的操作过程，叙述操作方法，让他们学会最少时间的计算。这样会使学生产生一种错觉：数学是一种只有我先把事情做好，才能理解掌握的高深学问。大多数预习不到位的学生在没有操作流程引导下进行操作，会出现迷茫、困惑，甚至产生对数学的恐惧。适度的思考会激发学生思考的热情、参与的兴趣，而过度的思維跳跃，会让学生迷茫、畏惧。

这种课例确实能培养学生扎实的知识技能，学生能在不断重复的操作和叙述中，牢记知识与技能，但大多数学生的学习过程是沉闷、乏味的，他们无法对数学学习产生高涨的热情。这样的设计缺少对“烙饼问题”中优化思想的联想，使其成为一个孤立的问题，无法与握手情境、两两结合的情境产生串联，对学生思维品质的发展不利。从某一问题出发而能够触及同类问题的思想是教学的永恒追求。[2]

（二）重数学的抽象性  轻数学的指导性

数学广角是一组全新的学习素材，对知识的衔接与迁移要求不高。在这种情境下，教师可以破除“从生活实践中抽象出操作流程表及时间计算方法”的局限性，通过数学计算结果与实践惯性操作结果之间的差异冲突，构建“通过计算发现修正操作流程表指导生活实践”的新型数学课堂，这样能有效地降解数学难学的情绪，提高学生学习数学的兴趣。

一线教师基本上是从具体操作中去总结提炼烙饼的最佳方案，从而引导学生掌握烙饼的时间计算。这样会增加学生学习的难度，对操作流程的叙述容易产生混乱。其实，通过条件的分解，学生完全可以自己通过列式计算出所需的最少时间，并通过与不同实际操作的时间进行对比，明确计算出最优化的时间。当实际操作时间大于计算时间时，教师要引导学生反思操作流程、观察流程、优化流程，让学生用数学问题的结果去指导生活中的实际操作。进而触类旁通，联想到“两两组合”，联想到握手游戏的安排等。

二、教学环节设计及设计中的一些想法

（一）导课——小提示

（1）每张饼有正反两面，三张饼一共有几个面？

（2）如果一个锅每次最多可烙2张饼，那么6个面至少要烙几次？

（二）问题探究

1.情境呈现，信息提取

出示主题图中的语言信息，让学生提取烙饼规则要求，并进行操作性说明。

生：每次最多烙2张饼;两面都要烙;每面3分钟。

师：我们要把叙述性语言解读成操作性语言，哪个同学来说说。

生：（1） 一次可以烙1张饼，也可以烙2张饼;每次用时都是3分钟。

（2）每张饼烙完正面，要再烙反面。

2.实践操作，绘流程破冲突

（1）2张饼如何烙？需多长时间？

（2）4张饼如何烙？6张呢？…

2张一组，一组一组地烙，可以有效地推广到所有偶数张的情况。

（让学生觉得烙饼是一件很容易的事情，激起所有人参与的热情，为后面的冲突作铺垫）

（3）如何烙1，3，5张饼。

师：烙1张饼，该如何烙？需多长时间？

生：烙完正面烙反面，要6分钟。

师：因此，我们有的时候也会把信息“每面3分钟”，呈现为“烙一张饼要6分钟”。

出示主题图，理解题意：

爸爸、妈妈和我每人一张，要烙几张饼？（3张饼）

“尽快吃上饼”，要求烙的时候要尽量节省时间。

师：烙3张饼，该如何烙？需多长时间？

生1：先2张一组，再烙剩下的1张，要烙4次，共需12分钟。

师：大家同意他的方法吗？

生2：不同意，他这样烙，浪费了很多时间。

师：他为什么会浪费时间？浪费了多少时间？哪个同学能准确地告诉大家？

生3：烙一张时有空位，会浪费3分钟。

在学生迷茫困惑之时，教师应适当加把火，然后给予一些必要的引导，激起学生的好奇心，为破解难点点燃情绪。

师：数学问题不要靠猜，要有明确的思路和方法。同学们可结合课前的小提示，尝试列式计算一下烙3张饼所需的最少次数。

生列式计算：3张×2面÷每次2张=3次

现冲突：计算只要3次，而实际操作却要4次，是操作方法有问题，还是计算方法有问题？生活中碰到这种事情时怎么办？

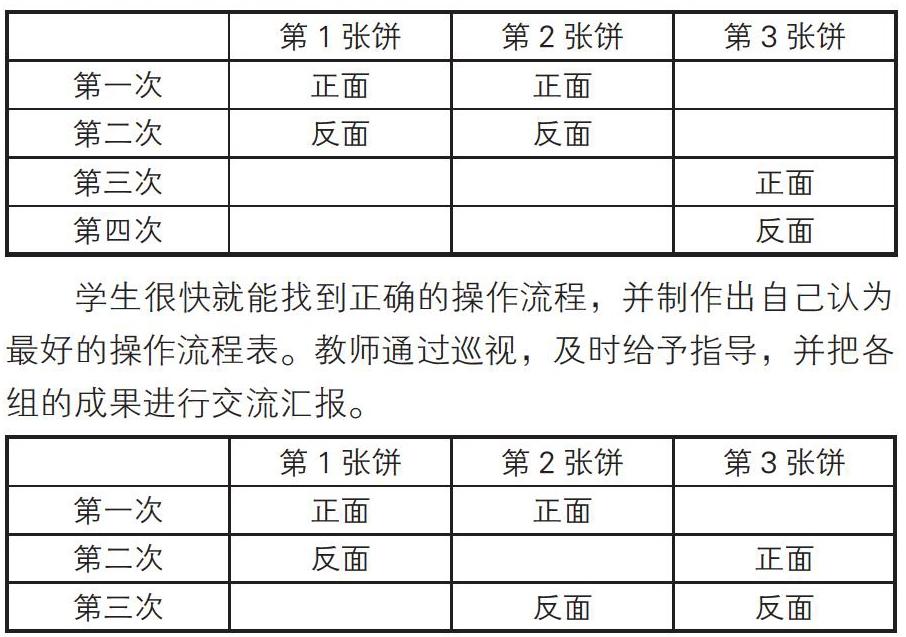
教师引导学生绘制数学流程表，并通过流程表来发现问题和解决问题。教师可以把上面学生1的烙饼方法制成一张操作流程表，观察其流程，看看有什么发现。

学生很快就能找到正确的操作流程，并制作出自己认为最好的操作流程表。教师通过巡视，及时给予指导，并把各组的成果进行交流汇报。

所需最少时间：3×3=9（分钟）  每次3分钟×3次=所需时间

原来数学可以通过计算，绘制数学流程表，指导我们在实践中优化时间。学好数学，能让我们从数学角度去解决很多实际问题。

接下来，学生根据操作表可以很轻松地进行正确的操作，但是要避免把数学课上成劳动课。

在烙饼的实践中，教师引导学生体验3张饼中“两两组合一次”的方式进行烙，让学生对具体操作有一个更直观的感知。[3]

第一次：第一张饼和第二张饼一起烙3分钟。第二次：第二张饼和第三张饼一起烙3分钟。第三次：第三张饼和第一张饼一起烙3分钟。

进而可以把上述的3张饼想象成三个小朋友，创设出情境：三个小朋友，每个人都有左右兩只手，他们要怎样才能把6只手两两握在一起？（注意不能把同一个人的两只手握在一起）并让学生叙述：我是第一张饼，第一次和第二张烙，第二次和第三张烙，第三次你们两个一起烙。

让学生初步感受到表示的不同方式方法，从而积累恰当的数学表达和表示的认知经验、优化的观念和有序思考的认知经验。教师让学生动手烙一烙，动动嘴巴说一说、看一看别人的操作，听一听同学的叙述，在多种感官的协同参与下，让抽象的感知融入学生的认知结构中去，并培养学生联想、情境串联的能力。

师：烙5张饼该怎样安排，才能使所需时间最少？

因为前面对1张饼和3张饼的讨论比较充分，学生对浪费时间和优化时间的情形印象深刻，所以很容易想到用3+2分成两组的方法。

师：7张、9张会安排吗？

奇数张，不能出现1张的情况，因此，先3张一组，以后每2张一组，一组一组地烙。

（三）总结拓展

1.总结

通过本节课的学习，我们知道，除了1张外，其他张数都可通过最优方案进行操作，最少时间可以直接通过列式计算得到。计算得到的时间一定是最少的，但要考虑是否能在操作中得到实现，烙饼的优化策略，就是为了使烙饼的实际操作时间等于计算时间。

在本节课限定的情境下：

烙饼的最少时间=饼的张数×2面÷每次2张×每次所需时间（1张除外）

完成相应的“做一做”练习。（要求先绘制流程表，再计算所需的最短时间）

2.拓展

妈妈要烙6张饼招待客人，每次最多可烙4张饼，每面都要烙，每面2分钟，最快几分钟可烙好？（要求先制作操作表，再计算所需时间，有兴趣的同学可以探究5张饼的情况）

参考文献：

[1]王光明，范文贵.新版课程标准解析与教学指导（小学数学）[M].北京：北京师范大学出版，2019.

[2]吴 飞.“烙饼”的数学建模和教学逻辑[J].福建教育学院学报，2016，17（2）：61-63.

[3]李 婷，卢建川.小学数学“烙饼问题”表征模型的比较与反思[J].数学教学通讯，2018（22）：26-28.