考虑组合风险的指数化投资与随机线性二次最优控制
2020-10-24李院德陈启宏
李院德, 陈启宏
(1.安徽省教育科学研究院,安徽 合肥 230061; 2.上海财经大学 数学学院计算科学与金融数据研究中心,上海 杨浦 200433)
0 引言
指数化投资是通过购买全部或者部分标的指数(例如S&P500、沪深300、恒生指数等)的成分证券,以追求组合收益率与指数收益率之间的跟踪误差最小化为业绩评价标准的投资方式。作为被动的投资组合方式,指数化投资具有能够使投资者享有市场平均收益水平、分散投资风险、投资成本低廉、投资组合透明化等优势,因此日益受到投资者的亲睐。 在经济整体陷于疲态的情况下,全球指数化投资产品规模继续维持稳定增长态势,截至2016年9月,全球ETF产品(交易型开放式指数基金)规模首次突破了3万亿美元,亚洲地区的ETF产品规模也创造历史新高,达到了3010亿美元。在我国,上市指数基金产品发展较快,形成了一定规模,并且仍然有很大的发展潜力。因此,关于指数化投资问题的研究颇具实际意义。
最早对指数化进行研究的是Treynor和 Black,他们在1973年提出了组合收益率的跟踪误差的计量方法[1],将跟踪误差定义为投资组合的收益率序列与目标指数收益率序列的线性回归中的残差的标准差。Perold在1984年采用均值方差模型对大规模证券投资组合进行优化[2],他在研究中指出均值方差模型也可以用于指数追踪。 Franks在1992年采用MV(均值—方差)模型研究基于基准组合的跟踪问题,通过最小化跟踪误差,仿真了50年的跟踪情况,得到了MV模型可以在低风险的情况下最小化跟踪误差的结果[3]。Pope and Yadav在1994年提出将跟踪误差定义为投资组合的收益率与目标指数收益率的差值序列的标准差[4]。Gaivoronski, Krylov和Nico van der Wijst在2005年采用了一种二次优化启发式算法,研究了在一个动态设置中选择和再平衡最优指数投资组合的问题[5]。近些年来,随着随机最优控制理论的发展,一些学者开始运用最优控制理论研究指数化投资问题,其中Browne在1999年利用随机控制的方法,研究连续时间情形如何使组合效用优于基准指数,并给出了相关的结论[6]。 Zhou在2006年利用随机最优控制的方法在连续情形下进行指数跟踪[7],并通过实证研究展示了运用随机最优控制方法进行指数化投资的现实意义。 2008年,Amott and Hsu指出了在不完美市场条件下,市值指数的投资组合会因为价格噪音而导致其绩效落后于非市值加权的投资组合绩效[8]。此外,国内对于指数化投资也有一些相应的研究,如董裕平和段嘉尚在2013年探讨了以我国A股市场上市公司的会计信息来编制基本面指数,并采用历史数据进行投资回测检验[9],该文也通过例子说明了研究开发一些适合我国资本市场发展阶段的可投资的策略性指数产品,有利于增加市场的长线投资需求,引导多种投资理念,培养多元投资方式。 为了消除参数的扰动对最优解产生的影响,安晓敏2016年在线性跟踪误差的指数化投资组合研究中,考虑了模型参数为矩形不确定集、椭球不确定集的鲁棒模型,通过实证发现该模型的解具有鲁棒性和最优性,且该模型与基准模型的收益一致性较好,但跟踪误差较基准模型大[10]。在商品指数化投资方面,李卓在2017年运用线性映射的方法估算了商品指数投资者的头寸,结合指数波动因子VIX以及标普500指数,构建了一个四元SVAR模型[11]。
股票市场指数是描述股票市场总的价格水平变化的指标,它是构成标的指数的成份股票的综合平均价格表现形式。指数化投资旨在追求组合收益率与指数收益率之间的跟踪误差最小化。若将市场标的指数中的各成份股票的数量按相同的比例缩小,使缩小后的标的指数的财富量I(t)与投资组合的财富总量x(t)在投资初期相等, 则可用|x(t)-I(t)|在时间上的累积量表示跟踪误差。于是指数化投资问题可以归结为一个随机线性二次最优控制问题。
类似于文献[7],本文考虑了连续时间和离散时间两种情形(对每种情形又分别讨论有限时区和无限时区两种情况),证明了在这两种情形下都能够找到最优的投资策略使得目标泛函取得最小值。之所以分别讨论有限时区和无限时区两种情况,一方面,从理论的角度,这是两种不同的类型,它们的求解方法有所不同;另一方面,从实际的角度,对于在特定时间段进行的指数化投资,需要考虑有限时区的情况,而对于永续存在的指数型基金,则需要考虑无限时区的情况。
作为指数化投资的业绩评价标准,本文提出极小化跟踪误差和投资组合的风险之和(其中风险用风险资产的累积方差来衡量),并假设组合风险在目标泛函中的的权重为λ(λ>0)。若λ→0+则表明投资组合只注重跟踪误差的最小化,即文献[7]的情形,本文在注记中将通过随机最优控制的例子予以说明。
另外,持有标的指数中的所有成份股在实际操作中是有难度的(尤其是对于规模较小的投资组合),本文假设指数化投资者是利用已选取好了的部分成份股票构建投资组合,至于如何选股则并不涉及。
1 指数化投资的控制模型
1.1 连续时间模型
假设在完备概率空间(Ω,F,Ft,P)中,某一个市场指数(例如S&P500)由m只成份股票组成(假设在所考虑时段内标的指数的构成不变),且每只股票的价格Si(t),i=1,2,…,m满足随机微分方程:
(1)
其中W(t)=(W1(t),…,Wm(t))T是m维标准布朗运动(t∈[0,T],W(0)=0)。此外,假定无风险债券满足:
dS0(t)=rS0(t)dt,S0(0)=S00
(2)


(3)
将市场上标的指数各成份股的数量按相同比例缩小,使调整后的成份股财富量与投资组合的财富总量在投资初期相等。调整后市场上标的指数成份股的财富量表示为(aj为调整后第j只股票的数量):
(4)
于是
(5)
用|x(t)-I(t)|在时间上的累积量表示跟踪误差,则指数化投资问题可以归结为如下的随机控制模型(其中e-2ρt是贴现因子,T<+∞为有限时区的情况,T=+∞为无限时区的情况):
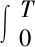
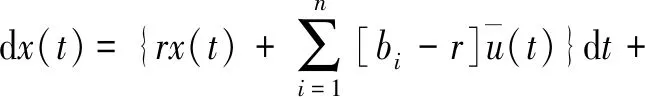
(x(0),I(0),Si(0))=(x0,I0,Si0)
(6)

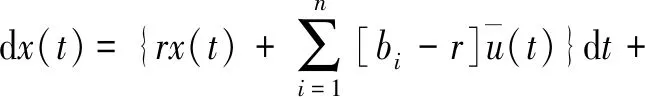

(x(0),I(0),S(0))=(x0,I0,Si0)
(7)
1.2 离散时间模型
在概率空间(Ω,F,P)中,假设某一市场指数由m只成份股组成(假设在所考虑时段内标的指数的构成不变),每只股票的价格Si(t),i=1,2,…,m满足下面的差分方程:
(8)
其中W(t)=(W1(t),W2(t),…,Wm(t))T是系统噪声,t∈{0,1,…,T}时间变量,且过程{W(t),t=0,1,…,T}是二阶平稳事件,均值和协方差满足E[Wi(t)]=0,E[Wi(k)Wi(l)]=δkl,其中δkl是Kronecker函数,i∈{1,2,…,n},k,l∈{0,1,…,T}。此外,假定无风险债券满足:
S0(t+1)=rS0(t),S0(0)=S00
(9)
考虑实际情况,我们假设bi>r>1。


(10)
将市场上标的指数各成份股的数量按相同比例缩小,使调整后的成份股财富量与投资组合的财富总量在投资初期相等。调整后市场上标的指数成份股的财富量表示为(aj为调整后第j只股票的数量):
(11)
则有:

(12)

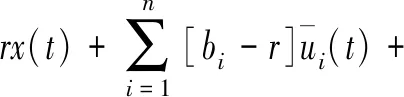
(x(0),I(0),Si(0))=(x0,I0,Si0)
(13)
2 最优策略的存在唯一性
2.1 连续时间情形
定义1对于系统
(14)
若存在一个反馈控制u(t)=KY(t),使得闭环系统
(15)
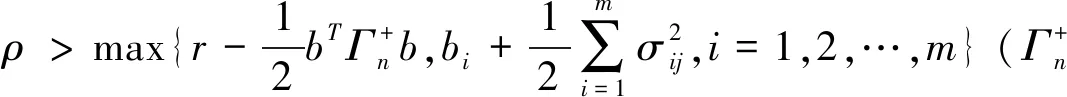
由于满足稳定性条件,系统(7)可以作如下变换:
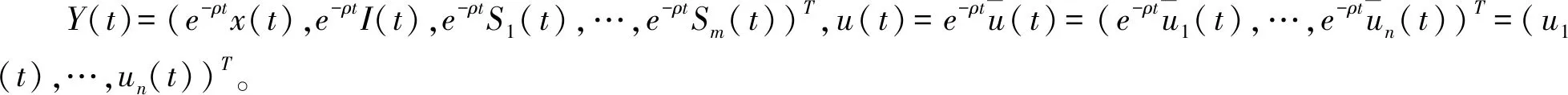
则(7)变成如下的随机线性二次最优控制问题:

s.t. dY(t)=[AY(t)+Bu(t)]dt+
Y(0)=y0
(16)
在连续时间情形,我们有如下结论(为了方便证明,我们先给出如下引理):
引理1对于线性微分方程:
(17)

证明由于方程(17)是线性的并且所有的系数是有界的,那么显然存在唯一的一个解P∈C([0,T];Sn)。现在考虑下列随机微分方程:
(18)
由文献[12]第一章定理6.14可知方程(18)存在唯一且可逆的解Φ(t)。 利用伊藤引理,可以得到

上面等式两边同在[t,T]上积分
Φ(T)TP(T)Φ(T)-Φ(t)TP(t)Φ(t)
于是推得
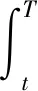
两边取期望(利用伊藤过程的鞅性质,最后一项伊藤积分的期望为0),可得
P(t)=E{[Φ(t)-1]TΦ(T)TGΦ(T)Φ(t)-1+
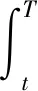
因为Q≥0,G≥0,所以P(t)≥0。
定理1(连续时间情形最优投资策略的存在唯一性)
(1)对于连续有限时区的情形,存在唯一的控制变量
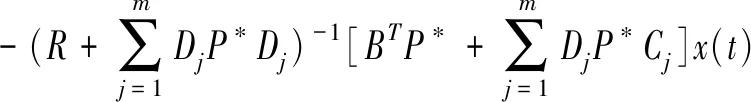
使得随机线性二次最优控制问题(16)的目标泛函取得最小值,即利用随机控制进行指数化投资时,存在唯一的最优策略使得跟踪误差与组合风险加权总和最小。其中P*、φ是以下方程的解:

(19)
(20)
(2)对于连续无限时区的情形,由于系统(16)均方能稳,则该系统存在唯一的控制变量
使得随机线性二次最优控制问题(16)的目标泛函取得最小值,即利用随机控制进行指数化投资时,存在唯一的最优策略使得跟踪误差与组合风险加权总和最小,其中Pmax是以下方程的最大解:

(21)
证明(1)随机线性二次最优控制的经典解法是借助于Riccati方程求解。若(19)和(20)有唯一解P*、φ,则系统(16)的最优控制为:
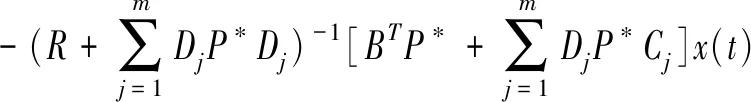
以下证明(19)和(20)存在唯一解。由之前的矩阵变换,显然有R>0,Q≥0,我们容易将式(19)变为:
(22)
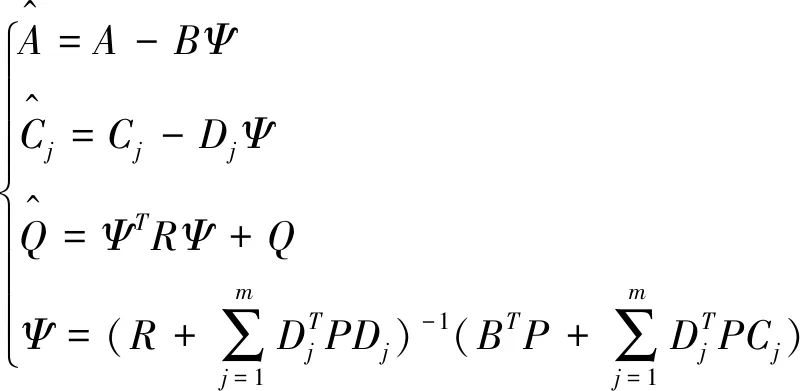
作如下迭代:
则可以得到一列Pi满足下面的方程:
由引理1可知Pi(t)≥0,下面我们证明Pt≥Pi+1。
首先我们同样可以写出Pi+1满足下面的方程:
两式相减可得:
(23)
令Δi=Pi-Pi+1,Λi=Ψi-Ψi-1,则有:

=B(Ψi-Ψi-1)=AΛi


又因为:
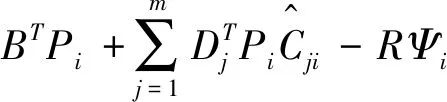
=0
则(23)式可以变为:
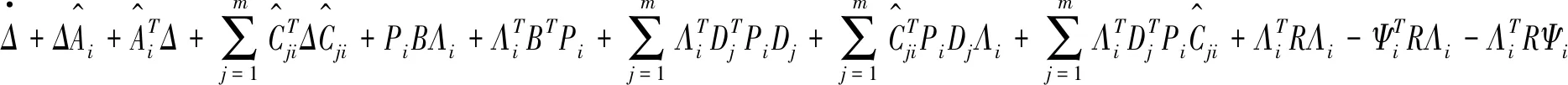

因为P1≥P2≥…≥Pi≥Pi+1≥…≥P≥0,则有:



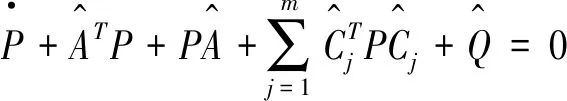
则有P为Riceati方程(19)的解。
下面证明唯一性:
假设P和P*是方程(2.8)的两个解,则它们分别满足如下方程:
(24)
(25)
再令Δ=P-P*,Λ=Ψ-Ψ*,其中Ψ*的定义与上面的相似,(24)~(25)则有:
由引理可知P≥P*,同理再令(25)~(24)同理可以证明P*≥P,从而便有P*=P,这就证明了唯一性。容易发现(22)是一个一阶线性微分方程,显然存在唯一解,从而定理得证。
(2)类似于有限时区的情形,无限时区的线性二次最优控制问题仍可借助于Riccati方程(19)求解,在系统(16)均方能稳的条件下若(19)有最大解Pmax,则(16)的最优控制即为:
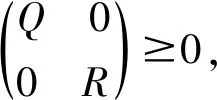
2.2 离散时间情形
定义2对于系统
(26)
若存在一个反馈控制u(t)=KY(t),使得闭环系统
(27)
定义3考虑下面的随机系统:

定义4对于以下系统:
(28)
若Z(t)≡0,a.s.,∀t∈N⟹Y(s)=0,则称系统 (A,A1,…,Am;C)(或(28))是精确能观的。
引理2若系统(A,A1,…,Am)是均方能稳的,则对任意的Q≥0,下面的Lyapunov方程:
(29)
存在唯一的解P≥0。

下面证明P是唯一的。在系统(26)中,令u(t)≡0,P(0)=P(1)=…=P(T+1)=P,从而对任意的Y(s)∈Rn,有:

Y(0)TPY(0)-E[Y(T+1)TPY(T+1)]=Y(0)TPY(0)-E[Y(T+1)TPY(T+1)]
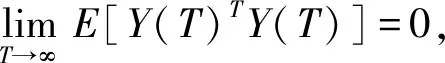
对于离散无限时区的情形,我们给出两个假设条件:
(L1)系统(A+BK,C1+D1K,…,Cm+DmK)是均方能稳的。
由于满足(L1),(L2),我们可以对系统(13)作如下变换:

则离散有限时区的控制模型转化为:

s.t.Y(t+1)=AY(t)+Bu(t)+
Y(0)=y0
(30)
在离散时间情形,我们有如下结论:
定理2(离散时间情形最优投资策略的存在唯一性)
(1)对于离散有限时区的情形,存在唯一的控制变量

使得问题(30)的目标泛函取得最小值,即利用随机控制进行指数化投资时,存在唯一的最优策略使得跟踪误差与组合风险加权总和最小,其中P*(t),t=0,…,T是如下Riccati方程的解:

(31)
(2)对于离散无限时区的情形,若系统还满足条件(L1)和(L2),则存在唯一的控制变量
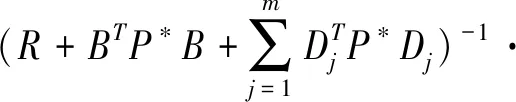
使得问题(30)的目标泛函取得最小值,即利用随机控制进行指数化投资时,存在唯一的最优策略使得跟踪误差与组合风险加权总和最小,其中P*(t),t=0,1,…,是如下Riccati方程的解:
(32)
证明(1)对于离散有限时区的情形问题(30)相应的Riccati方程为(31),由于(31)是有限时区差分方程,故存在唯一解P*(t),t=0,…,T,从而容易得到(31)存在唯一的最优控制。
(2)对于离散无限时区的情形,问题(30)相应的Riccati方程为(32)。以下证明在条件(L1)和(L2)下,(32)存在唯一解P*(t)>0,t=0,1,…:
第1步证明(32)有解P(t)≥0。 首先考虑有限时区离散LQ问题,我们的目标是寻找u(0),u(1),…,u(T),使得
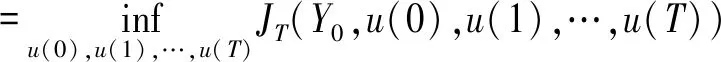
显然VT(Ys)随着T的增大而增大,且下面的Riccati方程:
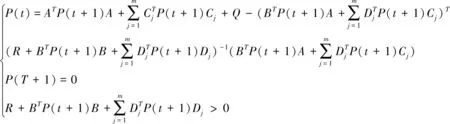


=VT1-t(Y0)≥VT-t(Y0)
又如果0≤t1≤t2≤T,显然有PT(t1)≥PT(t2),从而PT(t)相对于T是递增的,相对于t是递减的。
另一方面,因为系统(30)是稳定的,故存在u1(t)=K1Y(t)使得闭环系统(27)均方能稳,所以对任意的Y0∈Rn,存在常数c1满足:
此外还有:

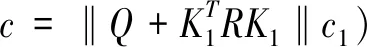
对于∀T∈N,∀t≤T有:
c‖Y0‖≥J(Y0,u1)≥V(Y0)≥VT-t(Y0)

第2步证明P>0且唯一。 先证明P>0,否则存在Ys≠0使得PY0=0,将(32)写成:
(33)
令u(t)=KY(t),则对任意的T∈N

=-E[Y(T+1)TP(T+1)]≤0

3 注记
上文证明了连续/离散情形下,运用随机线性二次最优控制进行指数化投资的最优策略的存在唯一性。人们自然会想到,当组合风险在业绩评价中的权重λ→0+(即投资组合只注重跟踪误差的最小化而不考虑降低组合风险)时,本文中最优投资策略的极限应该就是文献[7]的结果。以下我们将通过连续/离散情形随机最优控制的例子予以说明。
例1求解如下最优控制问题:

s.t. dx(t)=[x(t)+u(t)]dt+[x(t)+u(t)]dW(t)
x(0)=x0
解首先要求系统必须是均方能稳的,假设反馈控制为u(t)=ax(t),则有:
dx(t)=(1+a)x(t)dt+(1+a)x(t)dW(t)
由伊藤引理有:
dE(x(t)2)=(3+a)(1+a)E(x(t)2)dt




例2求解如下最优控制问题:

s.t. dx(t)=[x(t)+u(t)]dt+[x(t)+u(t)]dW(t)
x(0)=x0
解由例1知-3 由上可知,当ε→0+时,例2中最优控制的极限即是例1中的最优控制。 对于离散时间情形,我们给出如下例子: 例3求解如下最优控制问题: s.t.x(t+1)=[x(t)+u(t)]+u(t)W(t) x(0)=x0 解首先要求系统必须是均方能稳的,假设反馈控制为u(t)=ax(t),则有: Ex(t+1)2=(a+1)2Ex(t)2+a2Ex(t)2 =(2a2+2a+1)Ex(t)2 则当|(2a2+2a+1)|<1时,即-1 例4求解如下最优控制问题: s.t.x(t+1)=[x(t)+u(t)]+u(t)W(t) x(0)=x0 解首先要求系统必须是均方能稳的,假设反馈控制为u(t)=ax(t),由例3可知当-1 令ε→0+,对最优反馈控制变量两边取极限可得: 由上可知,当ε→0+时,例4中最优控制的极限即是例3中的最优控制。 本文将考虑组合风险的指数化投资问题归结为随机线性二次最优控制问题。 本文的主要结论是:对于有限时区的情况,无论是连续还是离散时间情形,最优控制都唯一存在,即利用随机最优控制进行指数化投资,最优投资策略唯一存在并且可以精确求解;对于无限时区的情况,在连续时间情形,本文证明了系统在均方能稳的条件下存在唯一的最优投资策略;在离散时间情形,当系统均方能稳且精确能观时最优投资策略是存在的,且相应的Riccati方程存在唯一的正定解。 本文还通过随机最优控制的例子说明了文献[7]所讨论的问题,可以视为本文的模型当λ→0+(即投资组合只注重跟踪误差的最小化而不考虑降低组合风险)时的极端情形。 然而,在实际投资中,由于各种外生因素的影响,往往需要不断调整模型的反馈控制函数的参数,以使目标系统达到最优状态。这样频繁的更新反馈控制往往会使系统陷入局部最优而不是全局最优。其实,这也是用数学模型来解决现实问题存在的一个共同的问题,值得进一步研究。 另外,由于侧重理论推导,未进行实证分析,本文模型对于市场实践的应用价值尚待检验,拟作进一步研究。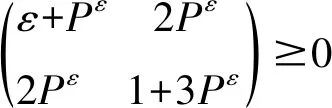

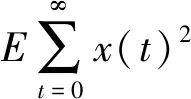


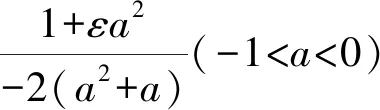

4 小结

