基于广义WOWA算子的Pythagorean模糊决策方法
2020-10-24沈志杰
李 鹏, 沈志杰
(江苏科技大学 经济管理学院,江苏 镇江 212003)
0 引言
Yager基于直觉模糊集提出了Pythagorean模糊集(PFS)的概念[1,2],并指出Pythagorean模糊集在描述模糊信息时具有更强的表现能力,引起了大量专家学者的关注。Zhang和Xu[3]定义了Pythagorean模糊数(PFN)的基本运算法则及距离公式。Ren等[4]考虑了决策者的“有限理性”,将Pythagorean模糊集与TODIM方法结合。Peng和Yang[5]将Choquet积分引入到Pythagorean模糊信息环境中,定义了Pythagorean模糊Choquet积分算子。Garg[6]将一些几何聚类算子推广到Pythagorean模糊环境中。刘卫锋等[7]在Pythagorean模糊环境下定义了诸多有序加权几何算子。
集结算子在信息集结方面具有诸多优势,目前已有大量的集结算子被应用于解决多属性决策问题[6~10]。有序加权(OWA)算子[11]是对数据进行从大到小重新排序,根据数据的位置进行加权再集结,现已被用于多目标生成树[12]、投资组合选择[13]、信息融合[14]等领域。加权有序加权(WOWA)算子[15,16]是在OWA算子基础上进一步考虑了信息本身的重要性,即属性权重融合了位置权重和客观权重。广义加权有序加权(GWOWA)算子[17]在保留WOWA算子优点的同时引入人工变量,增加了决策者对信息集结的控制能力。
然而,GWOWA算子在Pythagorean模糊环境下的研究尚不多见。因此,本文定义了广义Pythagorean模糊加权有序加权(PF-GWOWA)算子,讨论了PF-GWOWA算子的相关性质,并基于PF-GWOWA算子提出了决策方法。本文提出方法的优势在于:①综合考虑多属性决策矩阵中属性的位置权重和客观权重;②引入参数使得决策者掌握主动权,可以根据实际情况变动参数,调整决策模型;③将GWOWA算子拓展到Pythagorean模糊环境中,扩展了GWOWA算子的应用范围。
1 基本概念

为方便起见,称β=P(μβ,υβ)为Pythagorean模糊数。
定义2[3]设β=P(μβ,υβ)为任意Pythagorean模糊数,则称s(β)=(μβ)2-(υβ)2,h(β)=(μβ)2+(υβ)2,为β的得分函数与精确函数。
定义3[3]设Pythagorean模糊数βi=P(μβ,υβ)(i=1,2),则以下结论成立:
1)如果s(β1)>s(β2),则β1>β2;
2)如果s(β1)=s(β2),h(β1) 3)如果s(β1)=s(β2),h(β1)=h(β2),则β1~β2。 定义4[3]设βi=P(μβ,υβ)(i=1,2)为Pythagorean模糊数,则两者之间距离定义为: |(πβ1)2-(πβ2)2|) (1) 定义5[3]设Pythagorean模糊数β1=P(μβ1,υβ1),β2=P(μβ2,υβ2),β=P(μβ,υβ),则以下运算法则成立: GWOWA算子是一种广义的WOWA算子,它在保留WOWA算子特性的基础上引入参数λ,决策者可根据实际情况进行调节。本文将该算子推广到Pythagorean模糊环境中,提出广义Pythagorean模糊加权有序加权平均(PF-GWOWA)算子。 (2) 定理1设Pj=P(μj,υj)(j=1,2,…,n)为任意个Pythagorean模糊数,则通过式(2)进行集结仍为Pythagorean模糊数,并且满足 PF-GWOWA(P1,P2,…,Pn) v1(Pσ(1))λ+v2(Pσ(2))λ 因此,n=2时成立; 2)假设n=k时成立,即 因此,n=k+1时成立。 显然,根据1)和2)可知,对于任意的n,定理1均成立。 例1设P1=P(0.8,0.2),P2=P(0.7,0.4),P3=P(0.6,0.5),v=(0.3,0.5,0.2)T,λ=2,根据定理1可得: =P(0.7,0.3) PF-GWOWA(P1,P2,…,Pn) =ωσ(j) 进而可得: PF-GWOWA(P1,P2,…,Pn) 定理3设(P1,P2,…,Pk)为任意一组Pythagorean模糊数,Pj=P(μj,υj),j∈[1,k]。当λ=1时,式(2)退化为PF-GWOWA算子,即: PF-GWOWA(P1,P2,…,Pn) PF-GWOWA(P1,P2,…,Pn) 由于PF-GWA算子、PF-WOWA算子和PF-WA算子是PF-GWOWA算子的特殊情况,因此Pythagorean模糊数通过PF-GWA算子、PF-WOWA算子和PF-WA算子集结之后仍为Pythagorean模糊数。 设某决策问题,备选方案集为X={X1,X2,…,Xm},属性集为C={C1,C2,…,Cn},决策矩阵为G=(Pij)m×n(如表1所示),其中Pij=P(μij,υij)(i=1,2,…,m,j=1,2,…,n)为Pythagorean模糊数。 表1 Pythagorean模糊数多属性决策矩阵 (1)位置权重确定模型 设属性Cj的位置权重为wj(j=1,2,…,n),根据文献[11,21]可构建最大熵规划模型求解: (3) 其中α为人工变量,可根据决策者实际的乐观程度进行调节,满足0≤α≤1;disp(w)∈[0,ln(n)]。 (2)客观权重确定模型 离差最大化[22]方法是一种用于计算属性权重的有效方法。本文将离差最大化方法推广到Pythagorean模糊多属性决策矩阵中,进而求得客观权重。 在Pythagorean模糊决策矩阵G=(Pij)m×n中,属性Cj下,方案Xi和其它所有方案的离差值记为Tij: |(υij)2-(υij)2|+|(πij)2-(πlj)2|) 进而,属性Cj下所有方案和其它方案的离差值为Tj: |(υij)2-(υlj)2|+|(πij)2-(πlj)2|) 基于此,建立以下规划模型计算客观权重: (4) (5) (6) (3)基于WOWA算子权重方法的客观权重确定模型 通过WOWA权重算子[15]集结位置权重和客观权重,可得属性Cj在方案Xi下的综合权重vij: (7) (8) (4)决策步骤 综上所述,可得到基于PF-GWOWA算子的模糊决策方法决策步骤: Step1根据式(3)求得属性Cj的位置权重wj(j=1,2,…,n); Step2根据式(4)~(6)计算属性Cj的客观权重ωj(j=1,2,…,n); Step3根据式(7)~(8)得到属性Cj的综合权重vij(i=1,2,…,m;j=1,2,…,n); Step4根据式(2)确定各方案的综合属性值Vi(i=1,2,…,m); Step5根据得分函数s(Vi)对方案进行排序择优。 某地区发生地震,有4个受影响地区(X1,X2,X3,X4)需要支援[23],专家根据四个属性(C1,C2,C3,C4)对该4个地区进行评估,得到决策矩阵(如表2所示),其中C1指遇难人群的年龄、性别、身体健康情况,C2指遇难人员的伤残情况,C3指遇难人群所处的环境情况,C4指遇难的人数和地震发生的时间。 表2 决策矩阵 Step1利用式(3)算出位置权重,如表3所示。 表3 α取不同值时的位置权重 显然,当α=0.5时,各位置权重都为0.25,即数据排序后不受顺序的影响。同时,以α=0.5为分界线,上下两部分呈现出斜对称的规律。为消除各属性位置权重差距过于悬殊影响最终结果,分别选取α等于0.3、0.4、0.5、0.6、0.7时的位置权重进行计算。 Step2使用离差最大化的方法求出C1、C2、C3、C4的客观权重。根据式(4)建立二次规划模型如下所示: ωj≥0,(j=1,2,3,4) Step3根据式(7)~(8)求得属性的综合权重如表4至表8。 表4 α=0.3时综合权重情况 表5 α=0.4时综合权重情况 表6 α=0.5时综合权重情况 表7 α=0.6时综合权重情况 表8 α=0.7时综合权重情况 表9 各方案的综合属性值 Step4计算λ分别取1和2时,各方案综合属性值如表9所示。 Step5根据精确函数和得分函数对四个方案进行排序,如表10。 表10 方案优劣排序情况 显然,受参数的影响,PF-GWOWA在不同情况下会退化成其他算子。总体而言,当α取0.3和0.4时,方案X4为最优方案。当α取0.5、0.6和0.7时,方案X2为最优方案。可见,决策者的乐观程度影响着最终的最优方案,乐观程度越高,最优方案更趋向于方案X2,反之则更趋向于方案X4。 TOPSIS法[3]是对备选方案进行排序的常用决策方法。为了验证PF-GWOWA算子的有效性,本文用TOPSIS法对上述案例进行再次求解。 首先,求出正、负理想解分别为: X+={(C1,P(0.9,0.2)),(C2,P(0.7,0.4)),(C3,P(0.8,0.4)),(C4,P(0.7,0.3))}X-={(C1,P(0.3,0.8)),(C2,P(0.4,0.9)),(C3,P(0.5,0.7)),(C4,P(0.5,0.8))} 然后,算出各方案与正负理想解之间的距离,进而算出Xi与X+的接近程度RC(Xi)(i=1,2,3,4),最后根据RC(Xi)对个方案进行排序,如表11所示。 表11 各个方案与最优、最劣方案的距离、接近程度及排序 可以看出,用TOPSIS法求得的最佳方案为X1,但是它与排名二、三方案(X4和X2)的接近程度相差特别小。相反,根据表9与表10可知用PF-GWOWA算子及其退化算子求得的排名第二和第三方案之间的优劣差明显比TOPSIS法大,且排名前二的方案优劣差距也明显较大,但两方法算得的最劣方案皆为方案。综上所述,PF-GWOWA算子在处理优劣程度相似的方案时,扩大了方案之间的优劣差距,使决策者更易选出最优方案,使最终的结果相对更具说服力。 本文主要解决权重未知的Pythagorean模糊多属性决策问题。首先,提出了基于Pythagorean模糊数的GWOWA算子,并证明了该算子的一些性质;其次,根据OWA算子权重算法和离差最大化思想分别设计了该算子中位置权重与客观权重的计算模型,并基于该算子提出了决策方法;最后,通过算例分析和方法比较,说明了该模型的可行性。

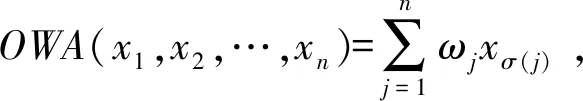
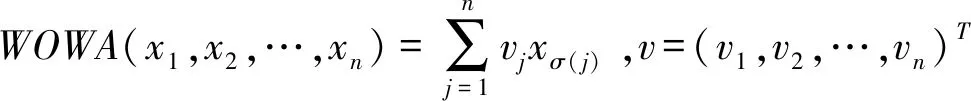

2 基于Pythagorean模糊数的GWOWA算子



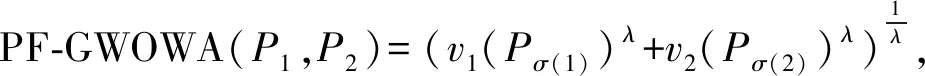
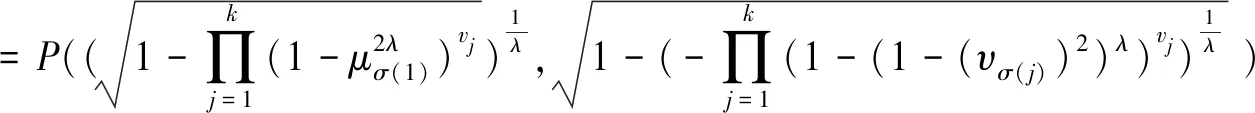







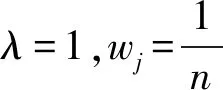

3 基于PF-GWOWA算子的决策模型
3.1 决策问题描述

3.2 基于PF-GWOWA算子的信息融合

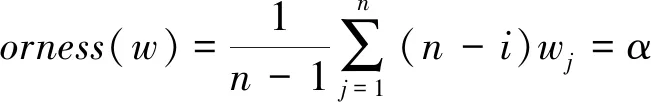




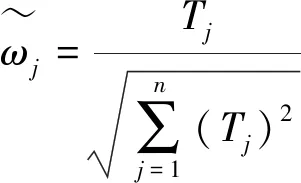


4 算例分析

4.1 决策过程










4.2 方法比较分析

5 结论
