基于APL的EWMA控制图经济统计优化设计

王海宇， 乔百豪， 瞿博阳

(1.郑州大学 商学院，河南 郑州 450001; 2.中原工学院 电信学院，河南 郑州 450007)

0 引言

作为过程质量控制的主要技术方法，控制图已经在工业生产中得到了广泛的应用。控制图设计好坏的主要评价指标可以分为统计特性与实施成本两种，即统计性和经济性，因此其优化设计主要包括统计性设计、经济性设计、经济统计性设计三种方法[1]。统计性设计的参数主要由控制图的两类错误确定，通常控制图的设计是在将误发报警的概率维持在一个较小的值的基础上尽可能地减小漏发报警的概率[2]。平均运行长度(ARL, Average Run Length)是目前最为普遍使用的控制图效率评价指标，它比较容易计算，便于被人们接受并使用[3]。由于ARL是样本数的平均值，受抽样频率等的影响较大，往往不能完全反映不同的控制图方案在监控效率上的差异[4]。

从经济层面上看，控制图设计同样会影响抽样、检验、异常来源查找及消除等的成本。因此，Duncan首先构建了X-bar控制图监控生产过程的费用函数，为控制图经济设计的研究奠定了基础[5]；Lorenzen和Vance考虑生产过程在寻找异常因素以及修复系统的时候是否停止运行，构建了通用的费用函数模型[6]。后续大多数控制图经济性设计的研究都是在这两篇文献的基础上发展来的。

为了兼顾控制图的统计性能与经济性能，人们又提出了过程质量控制的经济统计设计，综合考虑经济性和统计性，一些学者们在经济性设计上增加了统计性约束，使控制图在达到统计性能情况下成本最低[7]。对于控制图的经济统计设计来说，带有统计约束的经济设计并不是一种非常有效的方法，在很多实际应用中，统计特性都具有和经济特性同等重要的地位，因此成本和统计特性都应该作为设计目标同时进行优化[8,9]。Evans和Emberton提出了具有成本函数和统计指标两个设计目标的均值-极差控制图的优化设计，首次将控制图优化设计转化为多目标决策问题[10]；Safaei等提出了考虑田口质量损失函数的控制图经济统计优化设计模型[11]；Yang等以成本和ATS为经济统计多目标函数，以ARL作为统计约束，构造X和 S控制图的经济统计设计模型，并采用改进粒子群优化算法对该模型进行求解[12]。

由于休哈特常规控制图对小偏移不是很敏感，EWMA图被广泛地用于对过程中出现的较小波动进行质量监测。SEREL基于损失函数提出了EWMA图的经济性设计方法[13]；AMIRIA等基于成本和过程参数的不确定性构造了稳健的EWMA图经济设计和经济统计设计[14]；常志远等采用差分进化式烟花算法研究了自适应EWMA图的经济统计设计[15]。然而在这些已有的研究中，大都采用ARL、ATS等不够精确的性能评价指标作为统计性和经济性目标函数的计算依据，难以获得更准确的控制图性能评价结果和最佳的控制图优化设计方案。针对这一问题，本文采用更为精确的产品长度作为计算依据来讨论EWMA图的经济统计多目标优化设计的具体方法。

1 EWMA控制图的经济统计设计

(1)

其中，Z0=μ0，0<λ≤1，i=1,2,…。

(2)

控制图应用的一个质量周期是从生产过程开始到消除过程异常波动，包括过程处于受控状态、失控状态、排查异常、消除异常等多个阶段，如图1所示。

图1 控制图应用的质量周期示意图

在对EWMA图进行优化设计时，通常需要确定样本容量n、抽样间隔h、控制线参数k、平滑系数λ等参数，参数的选择既要考虑过程的统计性能，也要考虑其经济性，即控制图的经济统计设计。

1.1 统计性评价指标:APL的计算

对于控制图的统计性能，通常使用平均运行长度(ARL, Average Run Length)，即过程出现异常波动到该异常波动被控制图发现之间的平均样本数，作为评价指标。当过程处于受控状态时，希望有尽量少的虚发报警，即ARL0越大越好；当过程处于失控状态时，希望能够尽快发出异常报警，即ARL1越小越好。而ARL0和ARL1不可能同时达到最优，因此在控制图的统计优化设计中，往往将ARL0保持为一个较大的固定值，然后进行参数优化选择以使ARL1达到最小。但ARL往往存在度量不够精确，无法在样本容量、抽样间隔等有差异时有效进行控制图监控效率的衡量和比较，因此本文采用更为精确的平均产品长度(APL, Average Product Length)，即过程出现异常波动到该异常波动被控制图发现之间的平均产品数，作为评价指标。

首先，如图1中段所示，从过程出现异常波动到该波动被控制图发现之间生产的总产品数，即产品长度L可以表示为：

L=D+h(S-1)+nS

(3)

其中，n为样本容量；S为从过程出现异常波动到被发现之间抽样的样本个数；h表示样本之间间隔的产品数；D表示从过程出现异常波动到之后的第一个样本之间的产品数。

产品长度L的期望，即APL就可以表示为:

APL=E(D)+(n+h)E(S)-h

(4)

而EWMA图的ARL可以采用Markov链的方法进行求取。将EWMA图的控制限区间[UCL,LCL]等分成2m+1个子区间，其中，均值附近为一个小的子区间，上下控制限分别到均值子区间之间都等分为m份，这样每个子区间的宽度均为：

(5)

第i个子区间的中心位置为

(6)

当m足够大时，若EWMA统计量Z落入第i个子区间，则可以近似认为Zi=Yi。

pjk=P(到状态k│在状态j)

j,k=-m,-m+1,…,-1,0,1,…,m

(7)

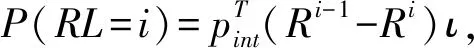
(8)

将式(8)代入式(4)中可得：

(9)

1.2 经济性评价指标：成本模型的计算

在以往的控制图经济性优化设计模型中，通常采用单位时间内产生的费用来衡量一个质量周期内的费用大小，即一个质量周期内的平均费用除以一个质量周期的平均时长。但这种评价方法同样存在不够精确甚至不能够很好反映生产现场真实情况的问题，比如当控制图出现报警，在确认该报警是否为误报警、查找异常原因、消除异常原因等阶段中，若过程处于停止状态，则这些停止状态的时间越长，一个质量周期的总时长也越长，单位时间内产生的费用就可能会减小，这显然与实际生产过程中要减少停机，尽可能保证连续生产的要求是不相符的。因此，本文提出了更精确的成本模型，单位产品的质量费用，即一个质量周期内的平均费用除以一个质量周期内生产的总产品数，进行控制图的经济性评价和设计。

(10)

其次，已有的控制图经济性优化设计模型通常假设受控和失控状态下单位时间内不合格产品的质量损失分别为固定的常数，这与生产过程的实际情况是不相符的，因此可以采用Taguchi二次损失函数来分别计算受控和失控状态下单位时间内的质量损失：

(11)

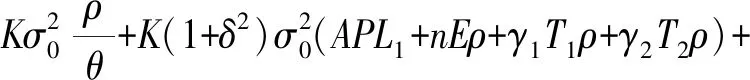
(12)

其中，γ2可以分别取0或者1，分别代表修复异常波动时生产过程停止或者继续；F表示每次误报警的平均费用；W为每次查找和消除异常波动的平均费用；a为一次抽样的平均固定成本；b为抽取一个样品的平均可变成本。

(13)

其中，N表示自然数集，控制限参数k的取值限定在0到4之间，EWMA平滑系数λ限定在0到1之间。

2 算例分析

取B=5000和B=10000两种情况，分别对偏移量δ=0.25、0.50和1.00三种不同的偏移程度，对EWMA控制图进行优化设计，其非劣解解集构成的帕累托前沿见图2所示。

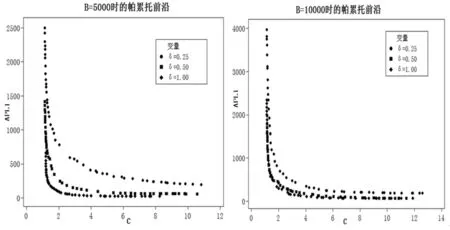
图2 不同偏移量对应的帕累托前沿

由于APL1表示的是失控时发现异常波动需要经过的产品个数，其取值为整数，因此通过取整和近似解的合并，得到不同的B值和偏移量δ组合下的非劣解各20组，结果如表1～6所示。

表1 EWMA控制图经济统计优化的帕累托解集(B=5000，δ=0.25)

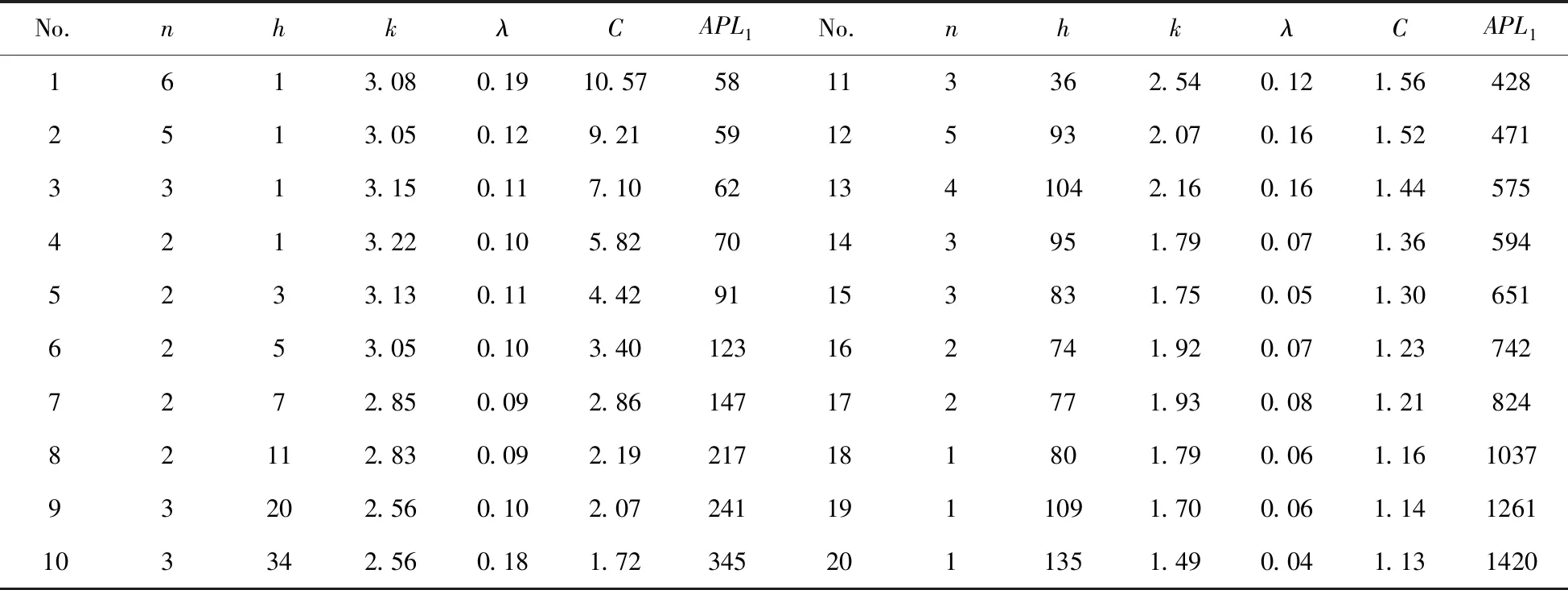
表2 EWMA控制图经济统计优化的帕累托解集(B=5000，δ=0.50)

表3 EWMA控制图经济统计优化的帕累托解集(B=5000，δ=1.00)

表4 EWMA控制图经济统计优化的帕累托解集(B=10000，δ=0.25)

表5 EWMA控制图经济统计优化的帕累托解集(B=10000，δ=0.50)

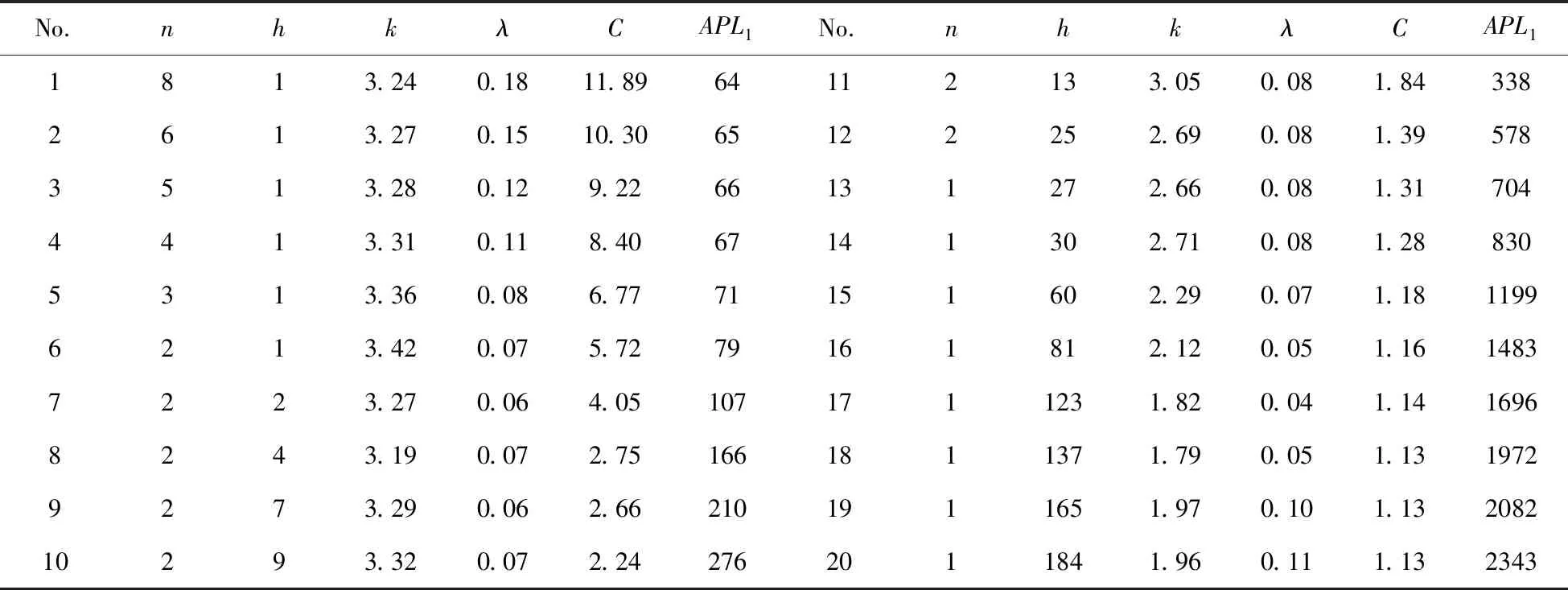
表6 EWMA控制图经济统计优化的帕累托解集(B=10000，δ=1.00)

表1～6分别给出了B和δ的不同取值组合下构造的多目标优化设计方案的多个非劣解，从这些解之间的变化可以发现，样本容量n的取值与成本C的变化成正比关系，与APL1的变化成反比关系；抽样间隔h正好相反，与成本的变化成反比关系，与APL1的变化成正比关系，这表明样本容量n对成本的影响比较显著，n越大，抽样检测成本、误报警成本等都会随之增大；而抽样间隔h对APL1的影响比较明显，h的增加必然会导致APL1的增大。控制线参数k和平滑系数λ的变化并无显著规律，这并不意味着这两个参数对成本C和APL1的影响不大，而是随着样本容量n和抽样间隔h的变化进行相应的调整，以实现两个控制目标的优化。

3 灵敏度分析

这里对控制模型中的三个主要设定参数：损失函数的系数K、单位时间生产的产品数ρ、过程处于受控状态的时间服从的指数分布的参数θ，分别进行灵敏度分析。将三个参数的设定值分别在第三节算例分析中表4(B=10000，δ=0.25)的取值的基础上增减20%，重新进行优化计算，结果见图3～5所示。

图3 参数K的变化对优化设计的影响

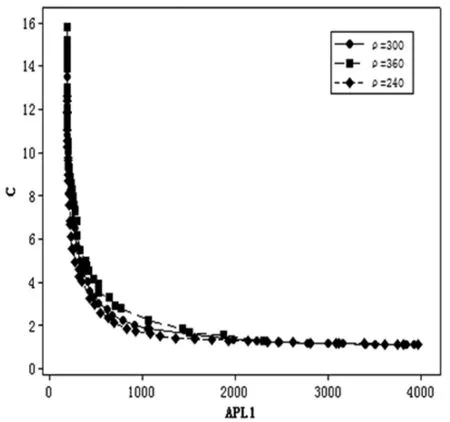
图4 参数ρ的变化对优化设计的影响

图3为参数K的取值分别为1、1.2、0.8时获得的多目标优化非劣解解集构成的帕累托前沿。由图可知，参数K的变化对该多目标优化设计的非劣解影响比较显著，随着参数K的增大，控制图的质量损失成本也将随之增大，这在图3中的帕累托前沿的前半部分(APL1<1000)的比较中体现的比较明显，在APL1的取值相同时，参数K越大的优化设计方案的非劣解的成本C越大；而对于帕累托前沿的后半部分(APL1>1000)，非劣解逐步趋向于成本降到最低限，这时候非劣解对参数K的变化逐步变得不灵敏，除非参数K出现成倍的增大或减小。

图4为参数ρ的取值分别为300、360、240时获得的多目标优化非劣解解集构成的帕累托前沿。由图可知，参数ρ的变化对该多目标优化设计的影响是不显著的，参数ρ的增大或减少并没有导致多目标优化设计的非劣解解集的分布曲线发生明显的变化，这说明该多目标优会设计方案对产品生产的速度快慢是比较稳健的，生产过程中出现生产速度的轻微变化将不会影响优化设计方案的具体应用。

图5 参数θ的变化对优化设计的影响

图5为参数θ的取值分别为0.02、0.024、0.016时获得的多目标优化非劣解解集构成的帕累托前沿。由图可知，参数θ的变化对该多目标优化设计的非劣解影响也是较为明显的，随着参数θ的增大，受控状态下的平均时长将缩短，一个质量周期的平均长度也会缩短，导致单位产品的平均质量成本将随之增大，这在图5的帕累托前沿的中间部分的比较中体现的较为明显。

4 比较分析

为了说明本文提出的经济统计设计方法的先进性，可分别与Serel等提出的EWMA图经济设计方法[13]、王海宇提出的基于APL的EWMA图统计设计方法[16]进行比较，见表7～9所示。

表7 三种EWMA图的优化设计方案比较(B=10000，δ=0.50)

表8 三种EWMA图的优化设计方案比较(B=10000，δ=1.50)

表9 三种EWMA图的优化设计方案比较(B=10000，δ=2.50)

5 结论

本文提出一种EWMA控制图的经济统计优化设计方法，经济性方面以单位产品平均质量费用为目标函数，统计性方面以失控状态下的平均产品长度为目标函数，在给定足够大的受控状态下的平均产品长度为约束的前提下，建立经济统计多目标优化模型来寻找更加合理的EWMA控制图控制参数优化设计解集。在实际应用中，相关人员可根据在统计性和经济性方面的偏好选择解集中的任意一个非劣解对应的参数设计结果作为EWMA图监控方案。