快速均值回归随机波动率模型参数估计及应用

李蓬实, 杨建辉, 林 焰

(1.东莞理工学院 经济与管理学院,广东 东莞 523106； 2.华南理工大学 工商管理学院,广东 广州 510640； 3.北京大学 汇丰商学院,深圳 100871)

0 引言

传统的期权定价模型假设波动率是常数, 根据该假设, 不同执行价格的同种标的资产的看涨期权应具有相同的波动率。 然而实证研究表明，从金融市场上的看涨期权价格推算出的波动率在平值期权(at the money)附近的波动率相对较低, 但随着期权的虚值程度(out of the money)或实值程度(in the money)增加波动率也逐渐增大。 这种现象被称为隐含波动率的“微笑曲线”(smile)现象。 隐含波动率的“微笑曲线”现象说明了在给定到期期限条件下, 隐含波动率与期权的在值程度或执行价格之间的关系并非固定不变的, 因此传统的期权定价模型中波动率为常数的假设并不符合现实。 除此之外, 隐含波动率“微笑曲线”还可能是由于标的资产价格的杠杆效应(标的资产价格与波动率之间的负相关关系)与标的资产价格的跳跃现象引起的, 然而传统的期权定价模型并没有考虑杠杆效应与资产价格的跳跃现象的存在。

为了解决传统期权模型中存在的问题, 学者们提出了各种方法来修正传统期权定价模型的缺陷。 其中两种主要的模型分别是跳跃扩散模型和随机波动率模型。 跳跃扩散模型比较适合解决到期期限较短的期权定价问题, 而随机波动率模型比较适合到期期限较长的期权定价问题。 Bakshi等[1]证明了跳跃扩散模型和随机波动率模型能够改进期权定价误差，同时也发现在考虑随机波动率之后引入随机跳跃只能够有限地减少期权定价误差。 因此, 本文主要研究随机波动率模型。

大量实证研究表明金融资产具有随机波动率的特点。 Chernov等[2]发现金融市场中股票价格的收益率具有明显的随机波动率性质。 刘志东等[3]研究了上证50股票指数及其成分股的高频数据后认为, 中国股市中约43%的风险来源于资产收益过程的随机波动风险。 通过对中国股市的研究，吴鑫育等[4]认为随机波动率模型能够更好地增加模型拟合度。 研究证明标的资产的波动率不仅具有随机的性质同时具有均值回归的特点，同时吴鑫育等[5]运用双杠杆门限随机波动率模型对中国股市进行实证研究发现，股市具有强波动率持续性以及显著的杠杆效应。 Liu等[6]通过对台湾金融市场数据的研究，发现外汇和股指市场中都存在均值回归的性质。 在实证研究的支撑下, 一般随机波动率模型假设波动率是由一个具有均值回归性质的扩散过程驱动。 Hull等[7]首先研究了具有随机波动率的金融资产的欧式期权定价问题。 Heston[8]假设随机方差(stochastic variance)服从CIR过程, 通过特征函数的方法推导出欧式看涨和看跌期权的解析解。

Fouque等[9]利用S&P500的数据证实了股指中存在的波动率聚集(volatility clustering)和波动率的快速均值(fast mean-reverting)回归现象, 在此基础上他们提出了一种基于快速均值回归的随机波动率模型, 该模型在衍生品定价方面得到广泛的应用。 Fouque等[10]在随机波动率是快速均值回归的扩散过程假设下, 利用奇异摄动分析方法推导出欧式看涨期权价格的近似解析解。 Wong等[11]研究了快速均值回归以及常数弹性波动率假设下涡轮期权(Turbo warrant)的定价问题。 通过引入违约风险中的随机波动率效应。 Fouque等[12]研究了可违约债券(defaultable bond)的定价问题, 并推导出近似解析解。 Yang等[13]在随机波动率框架下得到脆弱期权(vulnerable option)的近似解公式, 并研究了随机波动率对脆弱期权价格的影响。 Kim等[14]考虑了带有随机利率的随机波动率模型, 并证明了在较短的到期期限内新模型的对欧式期权定价效果要优于常数利率模型。

在上述研究成果的基础上, 本文研究基于快速均值回归随机波动率的双限期权(collar option)定价问题。 双限期权在到期时间T的收益可以表示为min(max(ST,K1),K2),其中K2>K1>0是期权的执行价格；ST是标的资产在T时刻的价格。 双限期权可帮助投资者锁定从投资的标的资产中赚得的利润, 还可以作为一种对冲策略使投资者避免标的资产价格剧烈变化所引起的投资风险。 除了可以对冲金融产品的风险, 双限期权还可以用于项目中的收益管理。 Yim等[15]提出将双限期权用于项目的物料采购, 用双限期权控制建筑项目中原材料的价格波动。

本文基于快速均值回归波动率的假设, 同时考虑了标的资产价格过程和驱动波动率扩散过程之间的相关性, 研究双限期权的定价问题。 由于考虑了波动率的随机性质, 期权价格难以直接获得, 因此本文采用Fouque等[10]的方法研究快速均值回归波动率框架下的期权定价。 该方法优点在于, 首先可以有效地减少随机波动率模型中的参数；其次可以通过较为简便的方法对简化后的模型参数进行估计；最后可以得到期权价格的近似解析解表达式。 本文的主要理论贡献在于：首先在快速均值回归随机波动率框架下研究双限期权, 由于双限期权在资产风险管理中的作用, 研究双限期权的定价问题具有一定现实意义; 其次, 对快速均值回归随机波动率模型中的参数进行了估计, 这些参数可以进一步应用到其它期权的定价研究中。

本文共分为五个部分。 第二部分介绍快速均值回归随机波动率模型；第三部分给出了基于快速均值回归随机波动率模型的参数估计公式；第四部分用金融市场数据估计了模型参数, 推导了考虑随机波动率的双限期权定价公式, 同时对双限期权价格进行了数值分析; 第五部分对本文进行总结。

1 模型

记标的资产在t时刻的价格为St,并假设标的资产满足以下随机微分方程

dSt=μStdt+f(Yt)StdWt

(1)

其中μ是标的资产的期望收益率,Wt是标准布朗运动,f(y)是大于零的光滑有界的函数,Yt是一个扩散过程。 与Black-Scholes模型中的常数波动率的假设不同, 式中的波动率是随机波动率。 假设驱动随机波动率的扩散过程是一个快速均值回归的OU过程,Yt满足以下随机微分方程

(2)

记为P*风险中性测度,γt为光滑的有界函数，表示波动率风险的市场价格。 根据Girsanov定理, 可得到在风险中性测度下的随机波动率模型

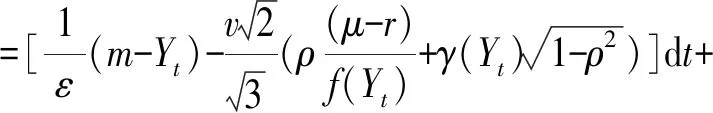
(3)

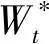
V(t,s,y)=E*[e-r(T-t)φ(ST)|St=s,Yt=y]

(4)

根据Feynman-Kac定理可知, 期权在t时刻的价格V(t,s,y)满足以下偏微分方程和终值条件

(5)

V(T,s,y)=φ(s)

(6)

将欧式期权在t时刻的价格V(t,s,y)以如下形式展开

(7)

利用Fouque等[10]提出的奇异摄动方法, 可以由上述偏微分方程和价格展开式得到关于欧式期权价格近似表达式。 由该方法得到的关于欧式期权价格的三个主要结论：

结论1展开式(7)中的第一项与y无关,且V0(t,s)满足以下偏微分方程和终值条件

(8)

V0(T,s)=φ(s)

(9)

(10)

其中τ是期权合约的到期期限,即τ=T-t；C1和C2是待定系数。

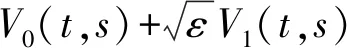
(11)

这种方法的优点在于可以有效地减少随机波动率模型中需要估计的参数的数量。 随机波动率模型涉及到的模型参数包括波动率扩散过程的均值水平、波动率的方差、波动率的均值回归速率、模型中两个随机过程的相关系数以及波动率风险的市场价格。 利用Fouque等[10]的方法，可以将上述五个模型参数包含到C1和C2两个系数中。 而C1和C2这两个系数可以通过金融市场中的看涨期权的隐含波动率的估计值得到。 这两个参数的估计方法在第3部分介绍。

2 模型参数估计

在给定期权到期时间T和执行价格K的条件下，可以从金融市场上观测到看涨期权在当前时刻的市场价格。 记该看涨期权的市场价格为Cmarket(K,T)。 所谓隐含波动率(Implied Volatility)指的是使金融市场观测到的实际期权价格与模型计算得到的理论价格相等的波动率数值。 一般将Black-Scholes期权定价公式作为计算隐含波动率的理论值的基准模型。 记隐含波动率为IV，根据隐含波动率的定义以下关系成立

Cmarket(K,T)=BSC(t,s,IV,K,T)

(12)

=sN(d1)-Ke-r(T-t)N(d2)+

(13)

其中，

=sN(d1)-Ke-r(T-t)N(d2)

(14)

(15)

(16)

BSC(t,s,IV,K,T)

(17)

将式(17)和市场实际价格的近似表达式代入式(12)后, 可知隐含波动率满足以下关系式

(18)

期权的在值程度(moneyness)指的是期权的实值或虚值程度, 定义为期权执行价格与标的资产价格的比值。 期权的隐含波动率变化可以通过期权的在值程度和期权的到期期限反映出来。 由(18)式能够进一步推导出隐含波动率IV,期权的在值程度K/s与期权的到期期限τ之间的近似线性关系。

引理1隐含波动率IV,期权的在值程度K/s与期权的到期期限τ满足以下线性关系。

(19)

(20)

(21)

根据式(19),可以利用线性回归方法估计出斜率α和β截距的值, 再利用(20)和(21)推算出C1和C2这两个参数。

3 实证分析及应用

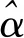
表1 斜率和截距估计值系数

得到斜率和截距的估计值后,可以根据(20)和(21)计算出快速均值回归随机波动率模型中的期权定价参数C1和C2:

(22)

(23)

(24)

从(24)可知,双限期权在到期时刻的价格等价于包含K1单位货币，一个多头头寸执行价格为K1的看涨期权和一个空头头寸执行价格为K2的看涨期权的资产组合。 因此双限期权在t时刻的价格为

(25)

其中C(Ki)为执行价格为Ki的欧式看涨期权在t时刻的价格。 众所周知，C(Ki)的表达式为

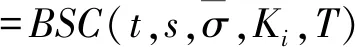
(26)

(27)

由于(25)是两个欧式看涨期权的线性组合,易知(25)应满足偏微分方程(8)。因此根据第2部分结论1可知,式(25)式快速均值回归随机波动率框架下,欧式双限期权近似解析解的第一项。在得到近似解析解的第一项之后，可以根据第2部分结论2得到近似解析解的第二项表达式

(28)

在快速均值回归随机波动率假设下，双限期权的价格Pt可以通过(25)和(28)式近似表示，即

(29)

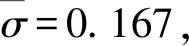
下面通过控制变量的方法进一步分析变量和参数对模型的影响。 取当期标的资产的价格的变动范围为[200,300],其它参数保持不变。根据式(25)和(29)可以分别得到常数波动率双限期权价格、随机波动率双限期权价格与标的资产价格之间的关系,如图1所示。根据式(28)可以得到双限期权近似表达式的修正项与标的资产之间的关系,如图2所示。

由图1可以看出,在考虑了随机波动率之后,双限期权的价格比常数波动率模型的价格较低。尤其在标的资产价格超过双期权合约两个执行价格的均值之后,两种不同模型给出的价格差异会更加明显。这个结果说明了,若只通过历史波动率和Black-Scholes常数波动率模型定价,很可能会高估了双限期权的价格,从而造成交易损失。由图2可知,在标的资产变化范围内，双限期权近似价格的修正项取值为负数,并且有随着标的资产价格增加而减少的趋势。因此考虑了快速回归随机波动率的双限期权价格小于常数波动率模型的价格主要是因为定价公式中的修正项的影响,反映了随机波动率对期权价格的影响程度。

图1 期权价格比较

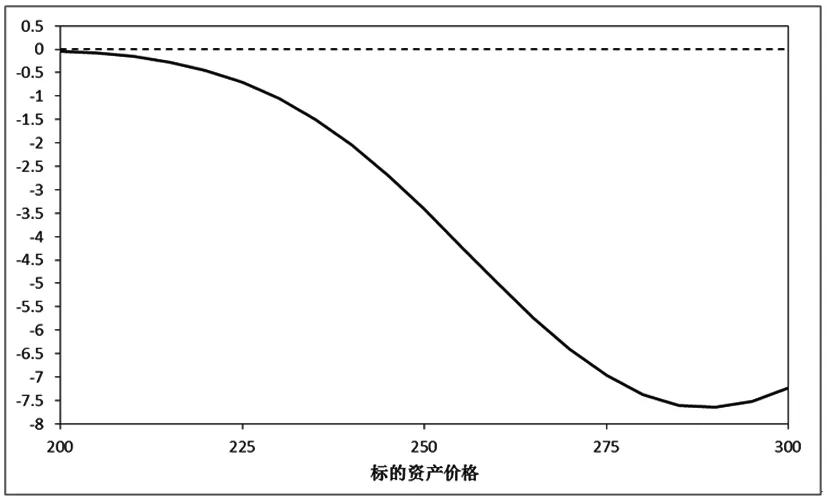
图2 双限期权修正项

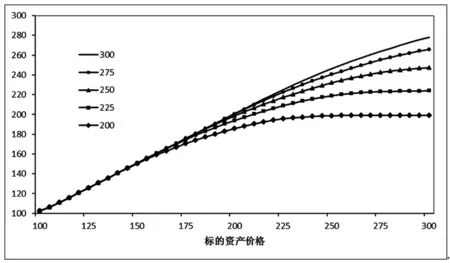
图3 执行价格对期权价格的影响

取当期标的资产的价格的变动范围为[100,300],期权执行价格K2的变动范围为[200,300],其它参数保持不变。根据式(29)可以得到具有不同执行价格的随机波动率双限期权价格与标的资产价格之间的关系,如图3所示。从图3可知,随着执行价格K2的增大,随机波动率双限期权的价格也较高。这个结论与常数波动率模型的定价是一致的,因此在随机波动率模型中,执行价格的变化并不会对双限期权的定价产生影响。

在上述的实证分析和应用中,我们首先利用金融市场上流动性较大的看涨期权的隐含波动率曲线估计出均值回归随机波动率模型中的两个参数,进而应用到双限期权的定价中。该方法与其它模型相比,具有两个较为明显的特点。首先减少了随机波动率模型(3)中需要估计的参数的个数,提高了效率;其次,可以先从流动性较大的期权(如欧式看涨期权)中估计出求解偏微分方程的参数,再应用到其它流动性较小的期权(双限期权)定价中,解决了某些奇异期权由于交易数据稀缺无法进行有效参数估计的问题。

4 结论

本文基于快速均值回归随机波动率模型,研究了双限期权的定价问题。双限期权可以对冲投资者由于标的资产价格波动造成的投资风险,因此研究双限期权定价问题对于金融市场中的现货和期权交易,以及金融市场的风险管理和控制具有一定的理论和现实意义。由于传统的期权定价模型中关于常数波动率的假设无法解释隐含波动率的“微笑曲线”现象,而快速均值回归随机波动率模型不但能够较好地解释隐含波动率的“微笑曲线”现象,还能够较好地解释标的资产收益的“尖峰厚尾”分布和波动率的“聚集”效应,因此在快速均值回归随机波动率模型框架下研究双限期权定价比较切合实际。本文通过市场隐含波动率的数据,估计了快速均值回归随机波动率模型中的两个参数,并应用到双限期权的定价计算中。在得到考虑了随机波动率的双限期权定价公式之后,对期权价格与标的资产价格之间的关系做了数值分析。基于快速均值回归随机波动率模型的期权定价方法可以进一步应用到其它的衍生品定价和资产组合管理中,这也是下一步研究的重要方向。