基于预防维修和质量损失函数的VSI EWMA控制图经济设计
2020-10-24薛丽
薛 丽
( 1.郑州航空工业管理学院 信息管理学院,河南 郑州 450046; 2.天津大学 管理与经济学部,天津 300072)
0 引言
统计过程控制(SPC)和维修决策是生产制造的重要工具,它们有助于提升生产过程的产品质量,降低控制成本[1]。在统计控制过程中,控制图被广泛地用来监控过程波动,当过程出现小波动时,EWMA控制图比传统的休哈特控制图有着更好的监控效果[2]。为了提高控制图的监控效率,Saccucci等人于1992年提出可变抽样区间EWMA控制图[3],研究结果表明可变抽样区间的EWMA控制图的监控效率明显优于固定抽样区间的EWMA控制图。随后,许多学者对它进行了研究[4~7]。其中,为了降低VSI EWMA 控制图监控过程的费用成本,Chou & Chen研究了质量特性值服从正态分布时,可变抽样区间的EWMA控制图的经济设计[8],根据Lorenzen & Vance模型[9]建立其经济模型。
基于产品生产过程中自动化和机器化的不断增加,生产流程也从人工到机器发生不断的转变。因此,设备状况在控制数量、质量及成本方面所扮演的角色日益重要。尽管工业界和学术界早已认识到设备维修和过程质量之间的紧密联系[10],但将设备维修决策与过程质量控制决策相互整合的研究近期才引起学者的广泛关注[11~14]。另一方面,由于测量费用很高,质量损失函数得到广泛的应用,它强调质量输出与目标值的偏离带来的损失,而传统的经济模型较少考虑这部分损失。因此, 为了提高过程监控效率的同时降低过程控制成本,本文将预防维修和VSI EWMA控制图进行联合经济设计,建立基于质量损失函数和预防维修的VSI EWMA控制图经济模型。
1 可变抽样区间EWMA均值控制图
设随机变量服从正态分布,其均值为μ,标准差为σ。当过程处于受控状态时,μ=μ0,σ=σ0(μ0和σ0分别为过程均值和标准差的目标值);当过程发生变化时,σ保持不变,μ=μ0+δσ。设Xi1,Xi2,…,Xin为第i时刻所抽取的容量为n的独立同分布的样本,则正态分布下的EWMA均值图的统计量为:
(1)

UCL=μ0+kσZ
(2)
LCL=μ0-kσZ
(3)

UWL=μ0+wσZ
(4)
LWL=μ0-wσZ
(5)
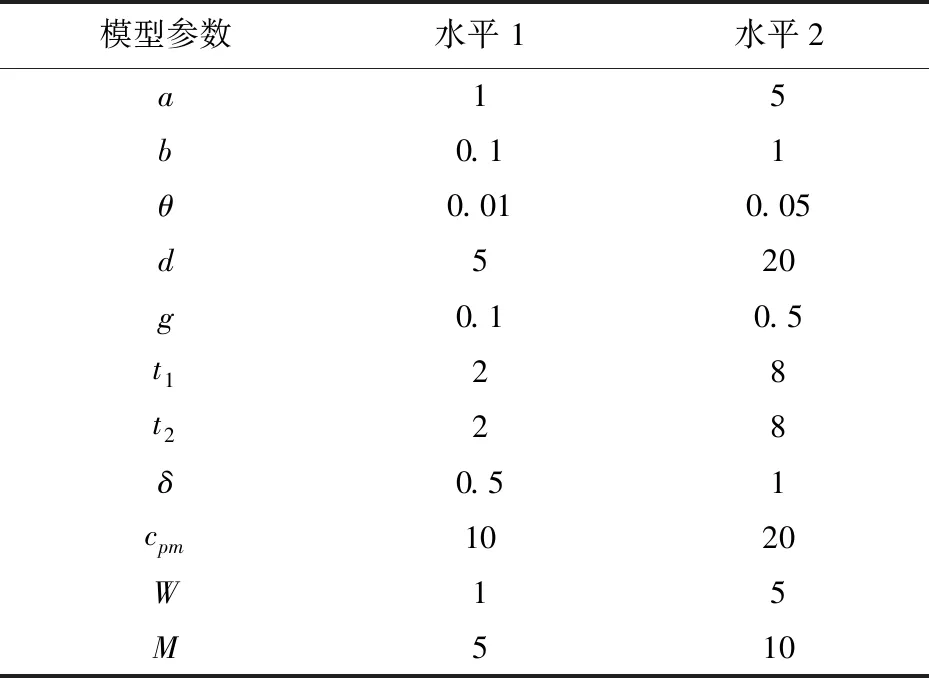
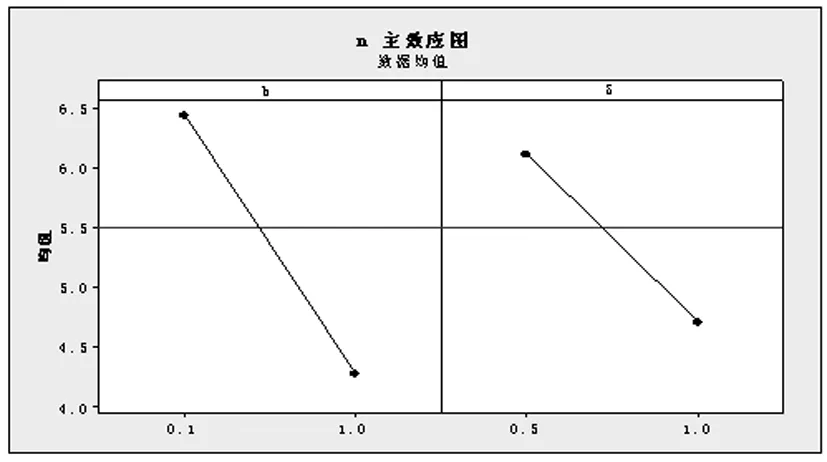
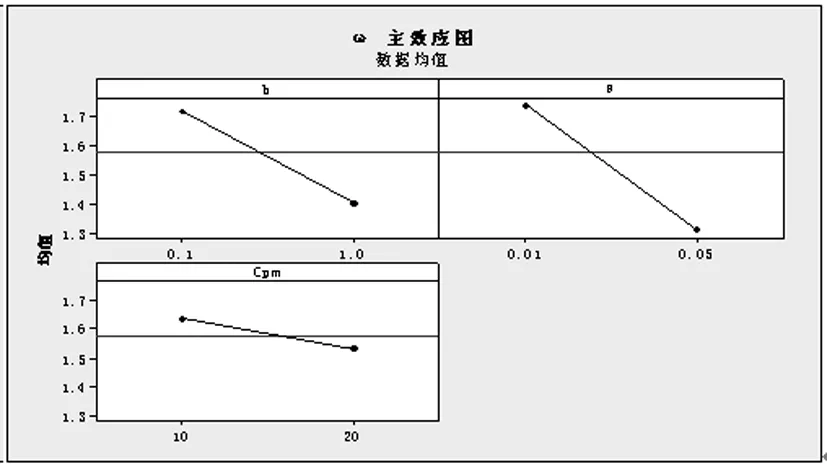
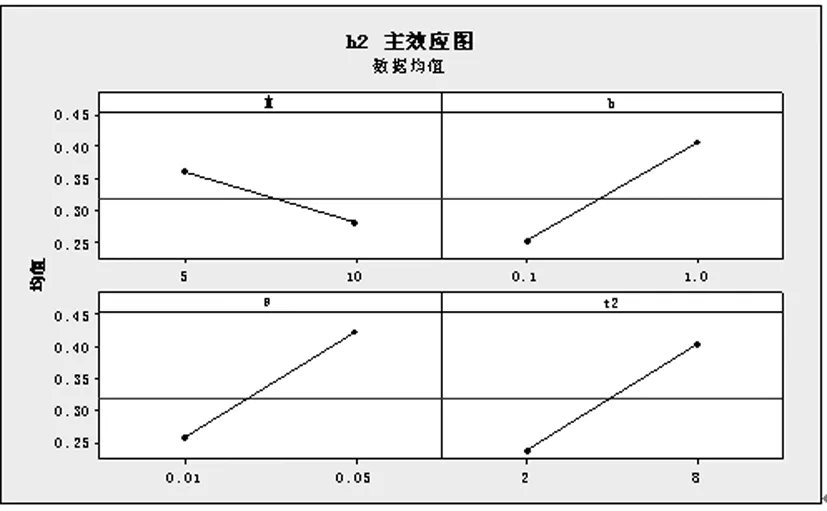
其中w是EWMA控制图警戒限的系数,且0 在建立经济模型之前,有以下几个假设: (1)过程一开始处于受控状态μ=μ0; (2)过程标准差σ不变; (3)质量特性值服从正态分布即X~N(μ,σ2); (4)若异常原因发生,过程均值变化到μ=μ1=μ0+δσ; (5)过程失控前的受控状态时间服从参数为λ指数分布; (6)在生产过程中只有一个异常原因,且抽样时异常原因不发生; (7)该过程的转变是瞬间的,它不可能自动回到受控状态; (8)当样本点落在控制图的警戒域时,立即进行预防维修。 将过程循环周期定义为从进入受控状态开始到失控,调查并消除系统原因所经历的时间。整个循环周期的期望由以下四部分组成:(1)受控阶段的时间;(2)从失控开始到发出失控警报的时间;(3)抽样和作图的时间;(4)寻找异常原因和纠正过程的时间。则过程循环周期T的公式如下: T=1/θ+(1-r1)st0/ANSS0+ATS1-τ+t1+t2+ng (6) 其中t0为寻找每个错误警报的平均时间; ANSS0为过程受控时报警所需的平均样本个数; s为过程受控时抽取样本的期望值,且s=e-θh0/(1-e-θh0)≈1/θh0; h0为平均抽样区间,h0=ATS0/ANSS0,其中ATS0为过程受控时,VSI EWMA控制图的平均报警时间; ATS1为过程失控时,VSI EWMA控制图的平均报警时间; t1为发现异常原因的平均时间; t2为纠正过程的平均时间; g为每次抽样和作图的平均时间; n为样本容量。 用马尔科夫链法可以得出ATS0和ATS1的计算公式如下: (7) 其中bj(j=1,…,2m+1)为统计量Zi处于状态Ej时所取的抽样间隔,当状态Ej为安全域时,bj=h1;当状态Ej为警戒域时,bj=h2。定义: Q=[qij](2m+1)×(2m+1)=(I-P)-1 (8) P=[pij](2m+1)×(2m+1) (9) (10) 同理, (11) (12) 同理,用马尔科夫链法可以得出ANSS0的计算公式如下: (13) 其中,qij的公式与ATS0中的qij定义一样,如式(8)、(9)、(10)。 在一个循环周期内,损失成本包括以下四方面: (1)发生错误警报的损失成本,抽样、检查、作图以及发现异常原因纠正过程的损失成本L1;(2)预防维修的成本L2;(3)过程失控时的损失成本L3;(4)过程失控时的损失成本L4。 (1)令d为每个错误警报发生的平均成本,W为发现及纠正一个异常原因平均成本,a为每个样本的固定费用,b为单元的抽样费用,则 (14) (2)令Cpm为每次预防维修的损失成本,则 (15) 其中p00和p01分别为过程受控时样本落在安全域和警戒域的概率,p10和p11分别为过程失控时样本落在安全域和警戒域的概率。 (3)假设质量特性值的规格限是m±Δ,这里m是目标值,Δ是容差,M是产品不合格时的损失,则损失函数的系数值为M/Δ2。假定过程仍处于受控状态,dv是均值和目标值之间的偏差,dv=|μ-m|,σ为过程标准差,则 (16) 其中y为单位时间的生产数量。 (4)当异常原因发生,过程处在失控状态时,产生的平均社会损失L4可表示为: (17) 由公式(14),(15),(16)和(17)可知损失成本函数L的公式如下: L=L1+L2+L3+L4 (18) 由公式(13)和(18)可知单位时间的损失成本函数ETL的公式如下: ETL=L/T (19) 通过前面的讨论可知单位时间的损失成本ETL是关于参数(n,h1,h2,k,w,λ)的函数,基于损失函数和预防维修的VSI EWMA控制图经济设计就是使单位时间的损失成本函数ETL最小确定这六个参数的最优值,于是得到一个完整的设计模型: (20) 下面给出一个算例说明如何根据VSI EWMA均值控制图的经济模型确定参数(n,h1,h2,k1,k2,w,λ)的最优解。 假设某一产品的生产过程,需要对某种质量特性值进行控制。根据收集的数据可知该质量特性值X~N(μ,σ2),当过程受控时,μ=μ0=4;当过程失控时,μ=μ1=μ0+μ0δ。模型参数和成本参数如下:a=1,b=0.5,σ=1,Δ=4,w=4,d=0.5,m=5,g=0.2hr,t1=0.5hr,t2=0.5hr,θ=0.01,γ1=γ2=1,δ=0.5,y=10,Cpm=10,M=10。 在matlab环境下编码遗传算法。所求控制图六个参数(n,h1,h2,k,w,λ)中,要求n为整数,h1,h2,k,w和λ为连续值。每个参数的取值范围为:1≤n≤25,1≤h13.5,0.01≤h2≤1,1≤k≤4,0.01≤w≤3,w≤k,0.01≤λ≤1。人口规模N为20; 交叉率为0.8;变异率为0.1;运行代数为100;适应度函数为损失成本函数ETL(如公式(19))。当遗传算法运行到100代时停止,得到VSI EWMA控制图的参数最优值:n=2,h1=2.5,h2=0.985,k1=2.097,w=0.5,λ=0.296,ETL=17.3247。 采用正交试验设计和回归分析对 VSI EWMA控制图的经济模型进行灵敏度分析。研究模型参数(a,b,θ,d,g,t1,t2,δ,Cpm,W,M)对设计参数(n,h1,h2,k,w,λ)和单位时间的损失成本函数ETL的影响,其中模型参数为自变量,设计参数和单位时间的期望费用为因变量。自变量(模型参数)分别对应的两个水平列在表1,这是一个十一因素两水平的试验,采用正交表L16(215)进行试验,共有十六次试验,每次试验用遗传算法求出模型的最优解(n,h1,h2,k,w,λ)。其余的模型参数的值分别固定如下:γ1=γ2=1、t0=1。根据正交表L16(215)所选取的十六次试验如表2,每次试验得出的结果分别记录在表3。 表1 十三个模型参数的两种水平 表2 根据L16(215)安排的十六次试验 表3 每次试验的结果 为研究模型参数对经济模型最优解的影响,令检验水平α=0.1,对每个因变量(设计参数或单位时间的期望费用)运用SPSS软件进行回归分析,由输出的方差分析表和回归分析表,得出以下结论: (1)过程均值波动δ和单元的抽样费用b对样本容量n的取值起作用,且样本容量n随着过程均值波动δ和单元抽样费用b的增大而减小。 (2)单元抽样费用b、异常原因发生的频率θ、每个错误警报发生的成本d和过程均值波动δ对控制线系数k的取值起作用,且控制线系数k随着单元抽样费用b、异常原因发生的频率θ的增大而减小,随着过程均值波动δ和每个错误警报发生的成本d的增大而增大。 (3)每个样本的固定费用a、每个错误警报发生的成本d、每次预防维修的损失成本Cpm和产品不合格时的损失M对长抽样区间h1的取值起作用,且长抽样区间h1随着每个样本的固定费用a的增大而增大,随着每个错误警报发生的成本d、每次预防维修的损失成本Cpm和产品不合格时的损失M的增大而减小。 (4)产品不合格时的损失M、单元抽样费用b、异常原因发生的频率θ和纠正过程的平均时间t2对短抽样区间h2的取值起作用,且短抽样区间h2随着产品不合格时的损失M的增大而减小,随着单元抽样费用b、异常原因发生的频率θ和纠正过程的平均时间t2的增大而增大。 (5)单元抽样费用b、异常原因发生的频率θ和每次预防维修的损失成本Cpm对警戒线系数w的取值起作用,且警戒线系数w随着单元抽样费用b和异常原因发生的频率θ的增大而减小,随着每次预防维修的损失成本Cpm的增大而增大。 (6)单元抽样费用b和发现及纠正一个异常原因平均成本W对平滑系数λ的取值起作用,且平滑系数λ随着他们的增大而减小。 (7)产品不合格时的损失M、过程均值波动δ、异常原因发生的频率θ、每个样本的固定费用a、发现异常原因的平均时间t1和每次预防维修的损失成本Cpm对单位时间的损失成本函数ETL的取值起作用,且单位时间的损失成本函数ETL随着它们增大而增大。 为了更能直观地显示出模型参数对控制图设计参数和单位时间的损失成本函数的影响关系,运用Minitab软件得到主效应分析图如图1~7: 图1 样本容量n主效应图 图2 平滑系数λ主效应图 图3 控制限系数k主效应图 图4 警戒限系数w主效应图 图5 长抽样间隔h1主效应图 图6 短抽样间隔h2主效应图 图7 单位时间的损失成本函数ETL主效应图 本文对基于预防维修和质量损失函数的VSI EWMA控制图进行经济设计研究。首先建立基于预防维修和质量损失函数的VSI EWMA控制图联合经济模型;使单位时间的期望损失成本函数最小来确定参数的最优值;其次用遗传算法来寻找联合经济模型的最优解,并给出工业中的一个例子。最后对联合经济模型进行灵敏度分析,得出控制图模型参数(a,b,θ,d,g,t1,t2,δ,Cpm,W,M)对设计参数(n,h1,h2,k,w,λ)的影响关系。2 经济模型建立
2.1 过程循环周期T的确定
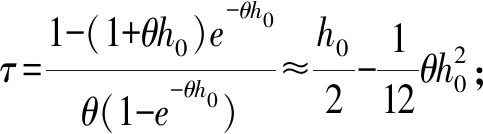

2.2 损失成本函数L的确定
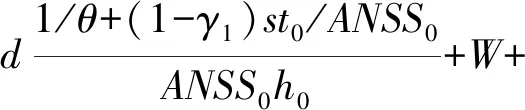
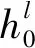
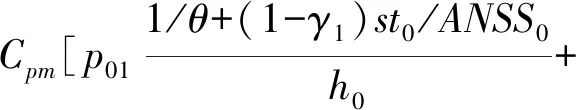
2.3 单位时间的损失成本函数ETL的确定

3 算例
4 灵敏度分析






5 结论
