互反判断矩阵一致性指标研究
2020-10-24徐迎军尹世久吴林海
徐迎军,尹世久,陈 默,吴林海
(1.曲阜师范大学 经济学院,山东 日照 276826; 2.江南大学 江苏省食品安全研究基地,江苏 无锡 214122)
0 引言
随着社会的不断发展以及人们需求的不断提高,决策分析中的问题变得日益复杂;知识更新的速度而往往会超过人们的认知速度;鉴于此,在决策分析中,如果让专家一次性直接给出所有备选方案的排序结果可能具有很大难度[1]。但若对决策问题进行分解,让专家一次只对两个备选方案进行比较并给出其重要性评价,则相对要容易得多。因此,在决策分析过程中,需要对多个备选方案进行综合排序时,可要求专家每次任意选取两个方案进行比较,在对所有方案对进行重要性比较之后,相应判断矩阵随即得到。紧接着的工作是,研究者选择适当方法,求得一组备选方案的综合排序结果。判断矩阵中的元素可取精确数字、区间数、三角模糊数等。若取精确数字,构造的判断矩阵称为数字判断矩阵,其主要有两种形式:互反判断矩阵[2~5]和互补判断矩阵[4~8]。徐泽水首次给出了互反判断矩阵和互补判断矩阵的概念,并把评估标度划分为互反性标度和互补性标度,给出了两类标度之间的密切联系,研究得出了两类标度之间的转换公式并对两类标度之间的关系进行了深入研究[5]。
如果基于问题的复杂性和专家认知的局限性,让专家每次只对两个方案进行比较,而我们最终需要求出所有方案的综合排序结果。由于专家能力的局限以及方法本身的局限性,得到的判断矩阵中部分元素可能会存在互相矛盾的现象,即存在不一致性问题。而若由不一致性判断矩阵或相互矛盾的判断矩阵出发,得到一组方案的综合排序,从而进行相关决策是不能令人满意的。因此,什么是一致性,如何判断一个矩阵是否满足一致性要求,对于不满足一致性的矩阵如何提高其一致性水平是一个重要的研究课题[9~15]。
对于未达到一致性要求的互反判断矩阵,徐泽水和魏翠萍等提出了一新颖的方法来提高其一致性程度[16]。即首先求取初始判断矩阵的排序向量,把求取的排序向量分量与初始判断矩阵的相应元素进行加权从而构建修正的判断矩阵,依次迭代进行下去。给出的定理显示修正判断矩阵的一致性水平高于初始判断矩阵,如果修正判断矩阵的一致性水平未达到事先给定的阈值要求,则只需要再进行此操作,使得修正判断矩阵的一致性水平继续提高,经过几次修正,修正判断矩阵的一致性水平一定能满足一致性要求。对于不满足一致性要求的互反判断矩阵,徐泽水提出了一个新的迭代方法,迭代方法利用原始判断矩阵特征向量对判断矩阵中偏差最大的列及其相应的行进行修正,以便提高原始判断矩阵的一致性水平[17]。提出的迭代方法易于计算机操作,且能尽可能多地保留原始判断矩阵的信息。田志友等利用原始判断矩阵的最大特征值及其Frobenius范数,给出了互反判断矩阵可能度和满意度的定义及其计算公式,并进一步把可能度和满意度集成为一个综合指标,称之为互反判断矩阵的可能满意度[18]。基于此,提出了提高互反判断矩阵一致性程度的修正算法。针对互反判断矩阵,Peláez等提出用三阶行列式的均值作为一致性指标,并把此思想推广到了互补判断矩阵中[19]。Stein等对互反判断矩阵进行了研究,基于一致性互反判断矩阵各列之和的性质,提出了新的互反判断矩阵一致性指标[20]。
对于另一种常见的判断矩阵互补判断矩阵,杨静等基于传统定义,构建了互补判断矩阵的模糊一致性指标;用来衡量互补判断矩阵的一致性程度;对于不满足一致性要求的互补判断矩阵,提出了修正算法。专家可根据此算法程序对不满足一致性要求的互补判断矩阵进行修正,此算法的优点在于其针对性强[21]。对于模糊判断矩阵,孙昭旭等提出了一新颖的互补一致性水平修正算法,此算法的基本原理是将三个极小化的最优化问题转化为一个目标规划问题,然后对此目标规划问题进行求解[22]。对于三角模糊数互补判断矩阵,杨莉等通过构建基于最小方差的多层次非线性规划模型对其加性一致性及其排序问题进行了初步研究[23]。
鉴于决策分析中问题的复杂性以及人们认知能力和决策方法的局限性,单一专家的建议难免存在不足之处,因此重大问题的决策中往往是专家团的集体参与,因此群决策问题是一个重要的研究领域。在群决策中,对于一组互反判断矩阵,徐泽水证明了若它们均具备可接受一致性要求,则由这组互反判断矩阵经过加权几何平均得到的集成判断矩阵仍满足一致性要求[24],这个重要结论为群决策的广泛应用奠定了重要基础。Dong等的研究表明若一组专家给出的所有个体判断矩阵的相容性指标均小于某个临界值,那么由此组个体判断矩阵经过加权代数平均集成获得的群体判断矩阵仍然满足可接受一致性要求[25]。Fedrizzi等考虑了个体偏好强度对互反判断矩阵一致性程度的影响,并构建了互反判断矩阵的新的一致性指标,并认为在群决策中在对个体专家的信息进行集成时,应该充分考虑到每个专家给出的个体互反判断矩阵的一致性水平[26]。本文基于互反判断矩阵与一致性互反判断矩阵集之间的距离,定义了一新的一致性指标。给出了一致性指标的度量方法。对于不满足一致性要求的互反判断矩阵,借鉴徐泽水和魏翠萍的思想[16],提出了一迭代方法来提高其一致性水平,并证明经过一定次数的迭代后得到的修正互反判断矩阵一定能满足设定的一致性水平。得出了群体互反判断矩阵一致性指标的下界。最后给出的数值例子显示了算法的可行性。
1 互反判断矩阵的若干定义

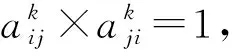
定义2称互反判断矩阵A=(aij)n×n是传递互反判断矩阵,若对任意aik≥1,akj≥1,有aij≥1成立,i,j,k=1,2,…,n。
定义3称互反判断矩阵A=(aij)n×n是一致性互反判断矩阵,如果aik×akj=aij,对任意i,j,k=1,2,…,n成立。
命题1一致性互反判断矩阵A=(aij)n×n一定是传递互反判断矩阵。
证明由定义2以及定义3易证命题1成立。
2 一致性指标的定义
定义4设A=(aij)n×n和B=(bij)n×n为两个互反判断矩阵,定义判断值aij与bij之间的距离如下:
(1)
命题2d(aij,bij)满足距离测度的三个条件:
(1)0≤d(aij,bij)<1;
(2)d(aij,bij)=0⟺aij=bij;
(3)d(aij,bij)=d(bij,aij)。


(2)证明:

⟺aij=bij
(3)由d(aij,bij)的定义知d(aij,bij)=d(bij,aij)成立。
定义5设A=(aij)n×n和B=(aij)n×n为两个互反判断矩阵,定义判断值aij与bij之间的相似度如下:
s(aij,bij)=1-d(aij,bij)
(2)
易知,0≤s(aij,bij)≤1。
定义6令A=(aij)n×n和B=(bij)n×n为两个互反判断矩阵,定义A和B之间的距离如下:
(3)
同样可得,d(A,B)满足:0≤d(A,B)<1。
定义7令A=(aij)n×n和B=(bij)n×n为两个互反判断矩阵,定义A和B之间的相似度如下:
(4)
易知,0≤S(A,B)≤1。
定义8设A=(aij)n×n为互反判断矩阵,SMn为n阶一致性互反判断矩阵集。定义A=(aij)n×n与SMn之间的距离如下:
(5)
易知,0≤d(A,SMn)<1。
定义9设A=(aij)n×n设为互反判断矩阵,SMn为n阶一致性互反判断矩阵集。令1-d(A,SMn)为互反判断矩阵A的一致性指标(CI),即:
CI(A)=1-d(A,SMn)
(6)
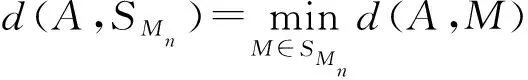
3 单人决策情形下的一致性改进算法

证明对任意i,j,k=1,2,…,n

定理2
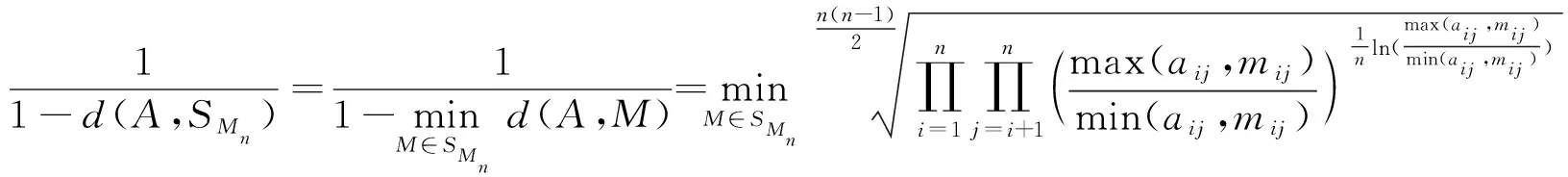
对上式两边取对数,并根据AHP中对数最小二乘排序法的相关理论得[3]:
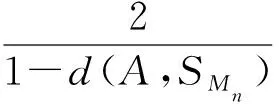
推论1
(7)
由(6)和定理2得推论1成立。
定义10如果CI(A)≥0.9,则称互反判断矩阵A为可接受一致性互反判断矩阵;否则,为不可接受一致性互反判断矩阵。

迭代算法(A1):
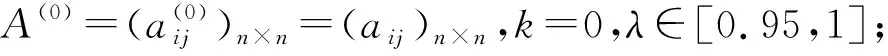

第三步:计算判断矩阵A(k)的一致性指标CI(A(k)),如果CI(A(k))≥0.9,转第五步;否则,转第四步;
下面的定理3保证了算法(A1)的可行性。
定理3令A为不可接受一致性判断矩阵。设{A(k)}为算法(A1)产生的矩阵序列,CI(A(k))为其相应的一致性指标。则有:CI(A(k+1))>CI(A(k))对任意k成立,而且:对任意给定的α0∈[0,1),存在k0,当k≥k0时,CI(A(k))≥α0。
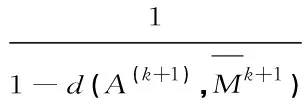

对(8)两边取对数,得:

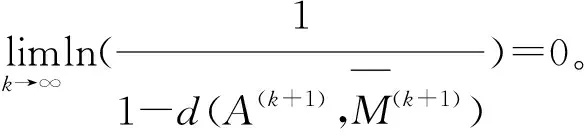
CI(A(k))序列单调递增,且极限为1,因此,存在k0,当k≥k0时,CI(A(k))≥α0。
定理3保证了对任意不具有可接受一致性的判断矩阵A,均可通过算法(A1)在有限步迭代后得到具有可接受一致性的判断矩阵。
4 群决策情形下群体判断矩阵一致性指标的下界
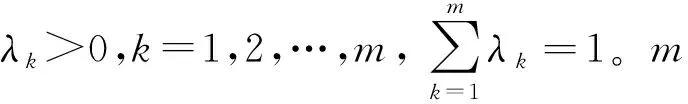
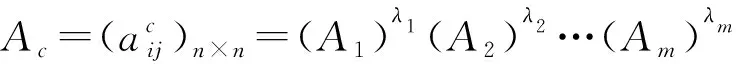
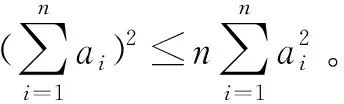
证明用数学归纳法易证命题成立。
定理4若CI(Ak)≥α0(k=1,2,…,m),则CI(Ac)≥(α0)n。
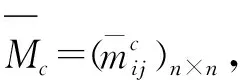

上式两边取对数,得:

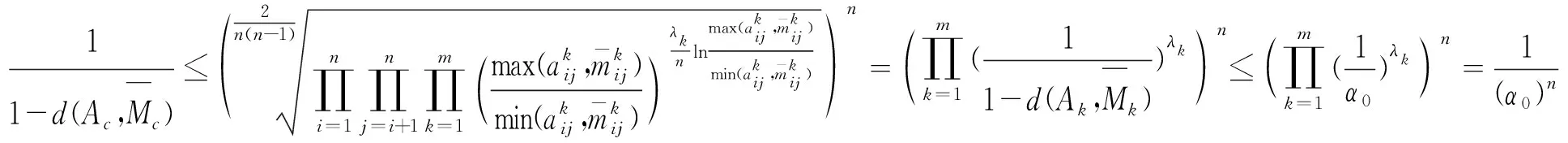
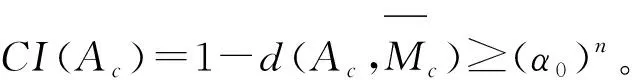
定理5假设A1,A2,…,An,B为n+1个判断矩阵。若S(Ak,B)≥α0,k=1,2,…,n,则S(Ac,B)≥(α0)n。
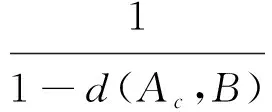
对上式两边取对数,可得:
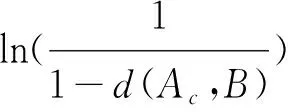

所以,S(Ac,B)=1-d(Ac,B)≥(α0)n。
5 示例
假设某位专家给出的判断矩阵A如下:

5.1 基于算法(A1)的修正

经过计算,得

取临界值α0为0.9. 一致性指标CI(A)=0.7928<0.9,为不可接受一致性判断矩阵。因此需要对判断矩阵A进行一致性修正。

第三步:计算判断矩阵A(0)的一致性指标,得CI(A(0))=0.7928<α0;转第四步;
转第二步:构造
计算判断矩阵A(1)的一致性指标,得CI(A(0)) 转第四步,对判断矩阵A(1)进行修正……经过9次迭代,得: 构造一致性矩阵 第一步:首先令A0=A,CI*=0.1,λ=0.95。 经过17次迭代,得 求得修正判断矩阵A17的最大特征值λmax为4.2538,从而一致性指标CI17为0.0950,小于0.1,满足一致性要求。因此,修正过程结束。得到最终的判断矩阵为A17。 算法(A1)与Xu和Wei方法得到的结果有所差别,这主要是一致性指标的设定原理不同造成的。两种一致性指标的比较分析需要进行更深入的研究。这也是作者下一步的努力方向。 5.3.1 定理4的数据示例 首先设有四位专家针对某决策问题给出了判断矩阵如下[24]: 假设可接受一致性指标临界值为α0=0.9。由(7)计算得四位专家给出的判断矩阵的一致性指标分别为: CI(A)=0.9668>0.9,CI(B)=0.9428>0.9 用(7)式求得群体判断矩阵的一致性指标为CI(A)=0.9494>0.9。这是定理4的一个数据例子。 5.3.2 定理5的数据示例 假设四位专家关于某问题给出的判断矩阵A1,A2,A3,A4分别为5.3.1中的A,B,C,D,第五位专家给出判断矩阵为: 文中首先定义了互反判断矩阵与一致性互反判断矩阵集之间的距离及相似度,并基于此距离和相似度定义了一个新的关于互反判断矩阵的一致性指标。给出了新一致性指标的度量方法。对于不满足一致性要求的互反判断矩阵,给出了一个迭代方法来提高判断矩阵的一致性水平,定理保证了经过一定次数的迭代后得到的修正的判断矩阵一定能满足预先给定的一致性要求。得出了群体互反判断矩阵一致性指标的下界,为新的一致性指标应用于群决策提供了理论基础。数值例子部分把提出的算法与Xu和Wei方法进行了比较,显示出文中提出的一致性指标和一致性修正算法的有效性和可行性。另外,对于群决策中定理4和定理5的结论也给出了数据示例。
5.2 基于Xu和Wei方法[16]的修正
5.3 群决策情形


CI(C)=0.9706>0.9,CI(D)=0.9594>0.9

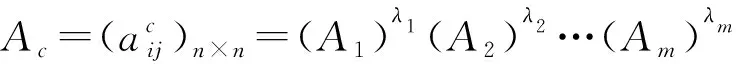
6 结束语
