信息不对称下的超对策冲突分析反问题研究

吴正稿，徐海燕，邓 潇

(南京航空航天大学 经济与管理学院，江苏 南京 211106)

0 引言

冲突具有普遍性，在经济、贸易、医疗及军事等各个领域都普遍存在着冲突。冲突的普遍性极大的促进了冲突分析理论的发展，以便辅助决策者理解、分析冲突和做出较优决策。冲突分析图模型理论[1～3](Graph Model for Conflict Resolution，GMCR)，为冲突的分析和解决提供了一种灵活、简单的方法。GMCR是在经典博弈论的基础上发展起来的，但经典博弈模型需要精准的偏好效用值。而GMCR只需要相对偏好信息，就能分析出冲突的均衡状态，是一种介于定性与定量分析之间的方法。GMCR可以最大限度地利用少量信息，为决策者提供科学的决策支持，因此被广泛运用于水污染冲突[4]、大气环境冲突[5]、能源冲突[6]、企业劳资冲突[7]和医疗保险冲突[8]等领域。而且GMCR有完善的建模和稳定性分析流程，并开发了成熟的决策支持系统[9,10]，使决策者能更加高效的分析冲突。Xu等[11，12]给出了 GMCR相关稳定性定义的矩阵表达式，用简洁的矩阵形式给出了GMCR稳定性的代数表达式，来代替原有复杂的逻辑表达，方便了冲突稳定性的求解，也促进了决策支持系统相关算法的实现。

GMCR能对不存在信息误解的冲突进行完善的分析，但对于存在信息误解的冲突，GMCR需要和其他理论相结合。目前国内外的学者一般运用超对策理论[13](hypergame，又称误对策)来研究存在信息误解的冲突。Bennett与Dando[14]最先运用超对策理论对二战期间法国的战败进行了分析。Fraser和Hipel[15]将冲突分析的F-H方法和超对策相结合，大大简化了超对策冲突的分析过程。Takahashi等[16]基于冲突分析理论，从状态角度分析超对策的均衡解，并进行了三阶超对策的应用研究。Wang等[17，18]将一般超对策理论拓展到高阶超对策并给出相应的解法。舒江等[19]提出“制约垒”概念，改进了超对策理论不能将决策目标和决策分析过程有机结合的缺点。郭文革和陈珽[20]将超对策模型拓展到最终报价仲裁领域。为了刻画局中人对超对策结局偏好认知的不确定性，宋业新等[21]构建了超对策偏好认知的信息沟通模型，并对均衡结局的鲁棒性进行了分析。Yasir等[22]基于超对策理论分析了冲突中的偏好误解和策略误解。刘德海和周婷婷[23]将误对策运用于恐怖袭击事件中，分析了政府反恐力量和恐怖分子的博弈。从目前关于超对策理论的相关文献中可以发现，现有超对策理论主要从正向视角出发，在已知所有决策者的误解信息的前提下，包括偏好误解和策略误解，运用超对策模型分析冲突中的个体稳定信息和整体均衡状态。虽然作为信息优势一方的决策者能比较容易的观察或分析出超对策冲突中真实的均衡状态，但现实中由于自身条件和认知能力的限制，很难获取对手误解的偏好信息。而冲突的反向视角能从均衡信息出发，求取对手误解的偏好信息，这是典型的冲突分析反问题研究。

对于冲突分析反问题的研究，Okada等[24]最早提出了不完全信息下的冲突分析反问题，在保证某个状态处于均衡的前提下，采用尝试法检验均衡状态的鲁棒性，但这种方法工作量大而且难以运用。Kinsara等[25]基于GMCR运用穷举法来获取使冲突方在某个状态处于稳定的所有偏好解，但这个方法的计算复杂度非常高。赵金帅和徐海燕[26]进行了有序偏好下的冲突分析反问题研究，在保证某一状态处于稳定的前提下，提出了最少约束条件下求取偏好解的方法，但依旧采用枚举法求解。Wang等[27]进行了基于矩阵形式的GMCR反问题研究，优化了原先的逻辑表达，但是仍然没有实现反问题的求解算法。

对于一个包含两个决策者的冲突，每个决策者不仅需要了解自身的偏好，还需要去获取其他决策者(对手)的偏好信息，来达到知己知彼的目的。但在信息不对称且对手处于信息劣势的冲突中，对手非常容易对决策者的偏好信息产生认知错误。当这种情况发生时，如果决策者能在谈判中察觉到对手对自身的偏好存在误解，更进一步的，如果决策者能够获得对手误解的偏好，那么决策者就可以在冲突谈判中占据主动优势，并通过设计相应的诱导机制来实现自身效益的最大化。实际上，尽管对手对决策者的偏好认知存在误差，但对手也是理性的，能正确推测决策者大部分的偏好信息。因此，可以认定对手对决策者偏好的认知误差会很小。基于以上分析，本文将超对策理论和冲突分析反问题相结合，在偏好误解最小化的前提下，以误解的偏好和真实偏好之间的差距为目标函数，求解满足稳定性约束的误解偏好，从而为超对策冲突诱导机制设计提供重要的决策支持。

本文第一部分介绍了冲突分析图模型和超对策的基本理论；第二部分针对两个决策者的冲突，详细介绍了在已知对手偏好的情况下，获取对手对决策者误解偏好的方法，即基于超对策理论的冲突分析反问题建模，并给出模型的求解方法；第三部分以电子商务环境下供应商和传统零售商之间的双渠道冲突为例，进一步验证了模型的有效性；第四部分总结并给出未来的研究方向。

1 基础理论介绍

1.1 冲突分析图模型

冲突分析图模型理论(GMCR)可以通过W={N,S,A,{≻i,～i:i∈N}}来表示。其中N={1,2,…,i,…,n}(n≥2)表示冲突中决策者的集合，n表示决策者的个数。S={s1,s2,…,sm}表示可行状态的集合，在图模型中表示顶点的集合，m表示可行状态集合中可行状态的个数。A={A1,A2,…,Ai,…Au}表示非空有向弧集合，其中Ai表示决策者i控制下的状态之间的一步可行转移，在图模型中表示顶点间弧的集合。对于决策者i(i∈N)的两个状态sp,sq∈S，其中p和q的取值范围为[1,m]内的整数，如果(sp,sq)∈Ai，就表示决策者i可以从状态sp做一步移动到状态sq。{≻i,～i:i∈N}表示决策者对于可行状态之间的简单偏好，其中表示对决策者而言状态sp优于状态sq，sp～isq或sq～isp表示对决策者而言状态sp等价于状态sq。偏好关系≻i满足不对称性，～i满足自反性和对称性，{≻i,～i:i∈K}满足完备性[11]。

1.2 冲突分析图模型的矩阵表示

设矩阵U=(U(p,q))m×m和V=(V(p,q))m×m，有L=U。V=(U(p,q)·V(p,q))m×m，其中U(p,q)和V(p,q)分别表示矩阵U和矩阵V中第p行q列的元素，“∘”表示Hadamard乘积。

如果矩阵Ji=(Ji(p,q))m×m满足下列式子：

(1)

则称Ji为决策者i的可达矩阵。Ji中第p行q列的元素相当于第p个状态sp和第q个状态sq之间的比较结果。

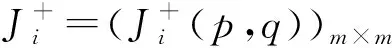
(2)

决策者i从初始状态sp出发通过一步改良可达的状态集合可以表示成：

(3)

(4)

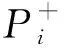
1.3 基于GMCR的超对策冲突分析理论

在信息不对称的冲突中，处于信息优势的决策者掌握了对方比较全面的信息，不容易对对方产生误解，而处于信息劣势的决策者缺乏对对方全面的了解，非常容易对对方产生误解。又因为在大多数冲突中，偏好信息非常难以掌握，常常存在误解，而关于决策者策略的信息比较容易掌握，不容易存在误解。因此，本文只考虑偏好误解的情况。

对于两个决策者N={i,j}的超对策冲突，把决策者i认知到的冲突记为Gi，决策者j认知到的冲突记为Gj。对于决策者i和决策者j，给出以下几种偏好矩阵的解释：

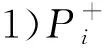
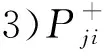
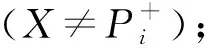
在冲突分析图模型中，当决策者无法从某个状态通过单边移动到达更好的状态，那么这个状态就称为该决策者的Nash稳定状态[28]。具体定义如下：

使决策者i和决策者j都处于Nash稳定的状态，称为冲突的Nash均衡解。

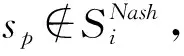
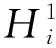
2 基于超对策冲突的反问题模型

2.1 反问题描述

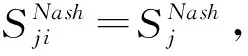
在冲突的初始阶段，决策者i与决策者j都没有意识到决策者j对决策者i存在偏好误解。此时，冲突双方在进行一阶超对策冲突。通过谈判，决策者i发现自己所认知的某些真实的Nash均衡解并不是决策者j认知的Nash均衡解，记这样的Nash均衡解的状态集合为SNash(对集合SNash进一步的解释是，该集合中的状态对于决策者i而言是Nash稳定的，但由于偏好误解，决策者j错误的认为该集合中的状态不是决策者i的Nash稳定状态)。那么，决策者i可以推断决策者j对自己的偏好产生了误解。此时，决策者i与决策者j之间的冲突就变成了二阶超对策冲突，如表1所示。

为了更全面的分析冲突局势，决策者i还需要充分掌握决策者j的误解偏好，以便做出有利的诱导或反击来实现自身利益的最大化。下文给出了求解决策者j对决策者i的误解偏好X的具体模型。

表1 信息优势方为决策者i的二阶超对策冲突

2.2 反问题模型构建

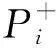
2.3 反问题模型求解

模型1是一个隐性的0-1线性规划问题，可以通过引入辅助变量将模型1转化成显性的0-1线性规划模型，以便于求解[29]。

命题1引入两组辅助变量Y(p,q)，a(p,q)∈{0,1}和无穷大的常数M，有模型1和模型2等价。

证明

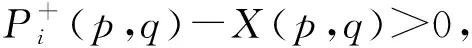
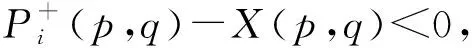
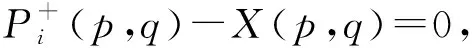
综上1)、2)、3)、4)可得模型1等价于0-1线性模型2，其中约束(10)表示变量的取值范围。

模型2:

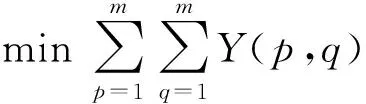
(10)

因为本文求解的偏好是相对偏好，所以使得某个决策者在某一状态处于稳定的解有很多个。一般的算法只能随机的求出0-1规划模型的某一个最优解，却无法求得所有的最优解。而实际谈判中决策者需要所有的最优解来了解对方所有可能的误解情况，以辅助自己作出较优的决策。为此需要引入求取模型2所有最优解的方法。不妨令Xα表示模型2一个既得的最优解，Zα表示最优解Xα对应的最优目标值。为了求出模型2中其它可能的最优解，需要在模型2中添加约束条件X≠Xα，来排除既得最优解Xα。求解其它最优解的模型如模型3所示。

模型3:

(11)

由于模型3中约束(11)是非线性的，使得整个模型变成非线性的。为了便于计算求解，需要将约束X≠Xα转化成线性约束。Combinatorial Benders’(CB)cuts[30]是采用线性约束来排除0-1规划模型中既得最优解的经典方法。借用该方法，可以将非线性约束(11)转化成线性约束。

令Bα表示矩阵Xα中元素值为1的位置集合，Nα表示矩阵Xα中元素值为0的位置集合,则有Bα={(p,q)|Xα(p,q)=1}和Nα={(p,q)|Xα(p,q)=0}。

定义2令|Bα|表示集合Bα的基数(集合Bα里元素的个数)，则称公式(12)为Xα对应的CB cuts:

(12)

由定义2易得引理1:

引理1如果X≠Xα,则有

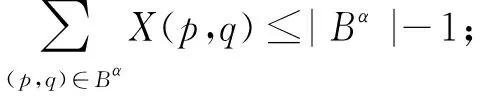
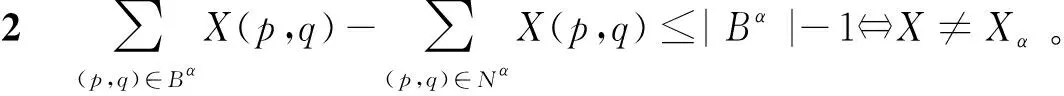
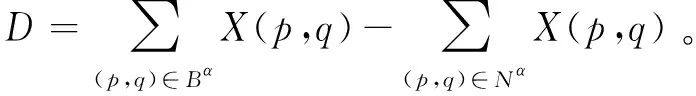
定理2揭示了公式(12)既排除了既得最优解Xα，又保留了其他所有的可行解。根据定理2，模型2可以通过添加Xα对应的CB cuts线性约束来排除既得最优解Xα，具体见模型4。

模型4:

(13)

为求解模型中所有最优解，需要在每求出一个最优解后，把该解对应的CB cuts加入到模型2的约束条件中，不断迭代，直到求得所有最优解。下文用Xc(c=0,1,2,3,…)表示模型2的解。求解模型2中所有最优解的具体算法为[31]：

步骤1令c=0，求解0-1线性规划模型2，得到初始最优解X0以及对应的目标函数值Z0。

步骤2令c=c+1，添加Xc-1对应的CB cuts到模型2的约束条件中，同时解出该模型的最优解Xc以及目标函数值Zc。

步骤3如果Zc=Z0，转步骤 2，否则转步骤4。

步骤4列出模型2的所有最优解Xl(l=0,1,…,c-1)。

3 案例分析

随着电子商务技术的发展，越来越多的供应商开始扩展网络直销渠道，极大提高了产品的市场份额和收益，但也引起了供应商网络直销渠道与传统零售渠道的冲突难题。针对这类双渠道供应链冲突问题，文献[32]构建了相应的冲突图模型。该冲突中有两个决策者：供应商(DM1)和传统零售商(DM2)。供应商有两个策略：1)协商，2)放弃(网络直销)。传统零售商有三个策略：3)退出，4)协商，5)竞争。该冲突可以构成的状态如表2所示，表中“N” 表示决策者不采取该策略，“Y” 表示决策者采取该策略，“-”表示既可以是“Y”，也可以是“N”。

表2 供应商与传统零售商双渠道冲突可行状态表

在冲突分析图模型中，策略优先权排序法是一种根据决策者的策略声明进行偏好排序的方法，相比直接排序法和策略权重法更加便捷高效[9,33]。所以，本文采用策略优先权排序法来求取供应商与传统零售商的偏好。根据双渠道冲突的实际背景，可以确定供应商与传统零售商的偏好声明，如表3所示。

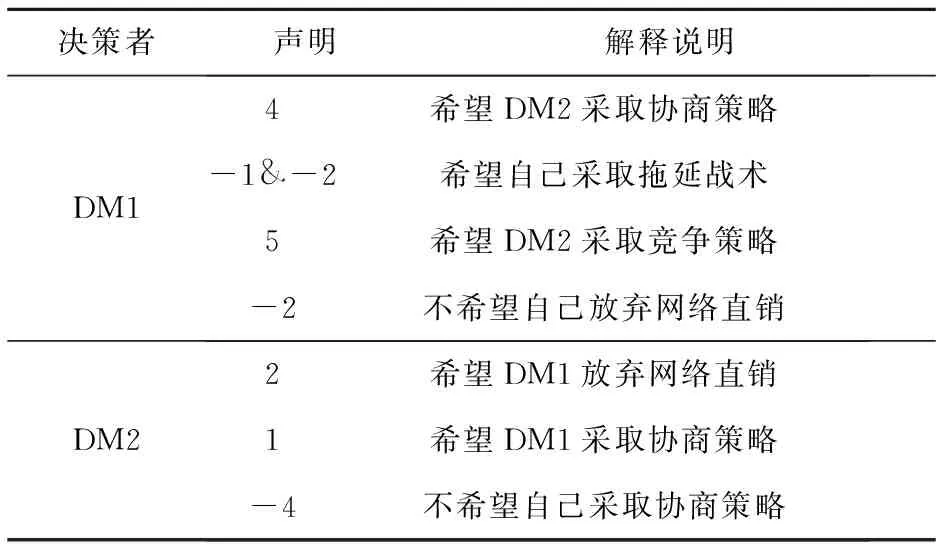
表3 双渠道冲突中各决策者偏好声明及其含义

根据表3给出的供应商与传统零售商的偏好声明，采用策略优先权排序法可以求出对于各决策者每个状态的分值大小，从而得到供应商和传统零售商相应的偏好排序：

s2≻1s5≻1s1≻1s3≻1s4≻1s6≻1s7

(14)

s7≻2s4≻2s6≻2s5≻2s1≻2s3≻2s2

(15)

具体的排序计算过程请参考文献[9]。

图1 供应商与传统零售商之间的双渠道冲突状态转移图

图1表示DM1和DM2的状态转移图，黑色圆点表示可行状态，弧的箭头方向表示由初始状态通过转移到另一个可行状态。

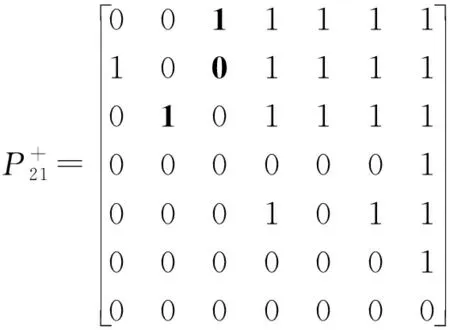
根据状态转移图，供应商与传统零售商相应的可达矩阵可以构造成：

根据上文中描述的偏好信息(14)和(15)，供应商和传统零售商相应的偏好矩阵可以构造成:

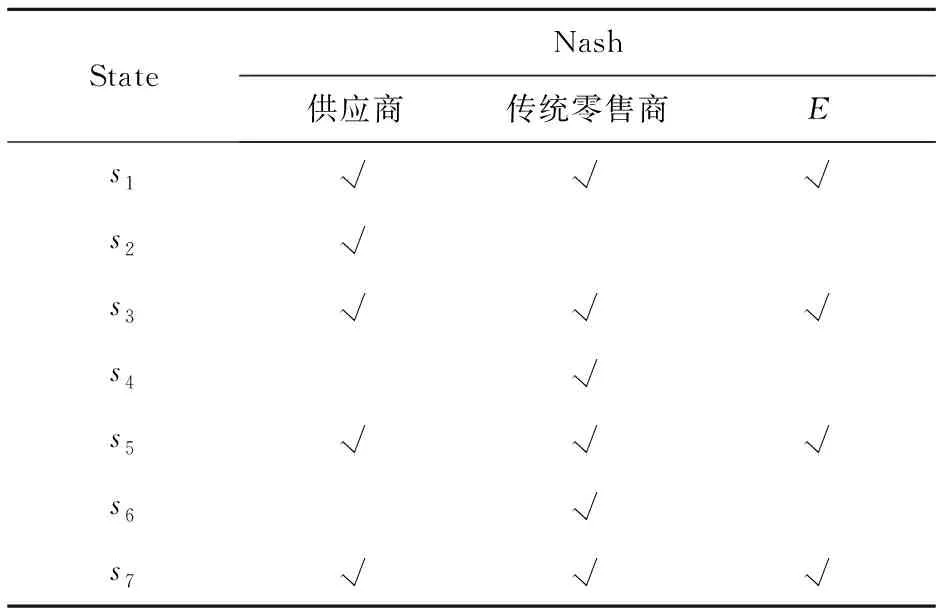
表4 传统零售商正确认知下的冲突稳定性结果

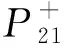
模型5:

(16)

(19)

运用文中第二部分的线性转换及算法求解，可得到模型5的所有最优解(解一和解二)。

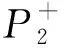
解一：供应商把s1≻2s2误解成s2≻2s1，把s1～2s3误解成s1≻2s3。

解二：供应商把s1～2s3误解成s3≻2s1，把s3≻2s2误解成s2≻2s3。

如果在误解情况下，供应商对传统零售商的偏好误解使冲突往不利于传统零售商的方向发展，那么传统零售商就可以向供应商透露自己真实的偏好来消除误解或改变自己的偏好来诱导供应商，从而使冲突往有利于自己的方向发展。

归纳为一般形式有：DM1对DM2的偏好产生误解，通过谈判DM2发现了DM1对自己产生误解，而DM1并未察觉自己对DM2产生了误解。那么DM2就可以通过本文的冲突分析反问题求解方法，确定DM1所误解的偏好。与不存在误解的冲突相比较，如果DM1对DM2的偏好误解使得冲突最后的均衡更有利于DM2，则DM2会继续让DM1误解下去；反之，如果DM1对DM2的偏好误解使得冲突局势往不利于DM2的方向发展，则DM2会通过消除DM1对自己的误解或改变自身偏好的方式来诱导冲突的发展，以实现自己利益的最大化。

表5 传统零售商为信息优势方的二阶超对策冲突稳定性分析结果

4 总结与未来展望

本文基于超对策理论，从冲突反向视角，建立了求取误解偏好的数学模型，并给了模型的求解思路，辅助决策者获取对手的误解偏好。决策者在获取这个偏好后便能制定相应的策略来诱导或欺骗对手，以使自身利益最大化。最后，以供应商与传统零售商之间的双渠道冲突案例进行了模型的应用研究，介绍了模型的构造与求解步骤，并求出了该冲突中所有可能的误解偏好。

本文方法与一般超对策方法和冲突分析反问题的具体比较见表6。本文方法与一般超对策方法相比，能够从冲突的反向视角出发，根据谈判中的均衡信息，构建具体的数学模型来准确求取误解偏好，克服了以往超对策只能假设误解偏好已知的缺点。本文方法与冲突分析反问题相比，能进一步分析存在偏好误解的冲突，且能够构建具体的优化模型并实现了求取偏好解的算法。至于如何根据本文方法求得的误解偏好来诱导对手按照自己设计的机制行动，以使自己获益最优，将是下一步研究的重点。

表6 本文方法与一般超对策方法和冲突分析反问题的比较