加权幂平均复合判断矩阵的群体AHP一致性研究
2020-10-24周金明苏为华朱晓临
周金明, 苏为华, 朱晓临
(1.安徽工程大学 数理学院,安徽 芜湖 241000; 2.浙江工商大学 统计与数学学院,浙江 杭州 310018; 3.合肥工业大学 数学学院,安徽 合肥 230009)
0 引言
运筹学家Saaty教授[1]提出的层次分析法 (Analytic Hierarchy Process,简记为AHP) 是一种实用的多准则决策方法。该方法把一个复杂决策问题表示为一个有序的递阶层次结构,通过专家的比较判断,计算各种决策方案在不同准则及总准则之下的相对重要性量度,从而据之对决策方案的优劣进行排序[1~4]。
专家判断的偏好关系已广泛应用于综合评价中,偏好关系的元素形式很多,主要有语言型[5~8]和数值型[9~13]两种偏好关系。群体综合评价问题中一般利用选择模型和共识模型处理偏好关系,并给出最终方案。选择模型,即集结方法和权向量法。在群体决策中使用的最广泛的两种集结方法就是判断矩阵的集结(AIJ)和权向量的集结(AIP)。当使用特征向量法作为权向量法时,一些学者对AIJ和AIP存在一些争议。Ramanathan和Ganesh[14]认为采用特征向量法作为权向量法时,AIJ法违背了Pareto准则[15],建议使用AIP法。Forman和Peniwati则认为AIP和AIJ的采用受不同的条件限制,是否使用AIJ或AIP取决于群体是否是一个合作的整体[16]。然而,当使用对数最小二乘法最为权向量法(RGMM)时,Barzilai和Golany表示AIJ和AIP是等价的[17]。然而,在共识模型中如何确定最终方案,关键在于专家个体偏好的集成以及一致性的共识判定。判断矩阵的一致性是群体综合评价的一个重要方面。一致性是所有决策者就所有可能的替代方案达成完全一致的意见[18~25]。事实上,在群体评价中,由于每个成员的知识结构,评判水平,个人偏以及信息的不确定性,多样性,模糊性等众多因素的影响,群体几乎不可能对所有问题达成完全一致的共识,以至于有时决策结果偏离客观现实太远,不具有说服力。因此,研究群体评价的共识模型具有重要意义。一致性测度[19,26]作为一种软共识测度不仅可以降低评价成本,而且可以衡量评价者之间的差异,也是共识模型的基础。
纵观现有文献,一方面,国内外学者关注群体AHP中判断矩阵的构造方法(正互反判断矩阵、互补判断矩阵),判断矩阵的灵敏度问题,一致性检验问题,判断矩阵的调整(修正)和标度选择合理性问题以及满意一致临界值(C.R.<0.1)的科学性等问题;另一方面,主要是判断矩阵的不确定数据属性选择问题即研究区间数AHP,三角(梯形)模糊数AHP,二元语义数AHP,直觉模糊数AHP,犹豫模糊AHP,云模型AHP等问题。然而,如何实现群体专家偏好的集结是群体AHP判断无法逃避的现实问题即如何实现复合判断矩阵的集成,它也是处理专家偏好的基础和核心内容。利用加权幂平均集成技术进行群体偏好意见的集结是有意义的。加权几何平均法是一种最常用的群体偏好集结方法,如果专家或决策者给出的判断矩阵具有完全一致性,则加权几何平均复合判断矩阵也具有完全一致性[27]。但是,若由专家给出的判断矩阵中有一些不具有完全一致性,则集结后的判断矩阵不具有完全一致性[28,29]。几何平均以及算术平均都是幂平均的特殊情形而已。关于其他幂次的加权幂平均复合判断矩阵一致性问题的研究并不多见;另外,考虑到群体AHP判断期望群体专家成员之间的意见趋同(收敛),采用加权调和平均平均复合判断矩阵方法进行群组判断矩阵的集成;进一步地,分析和研究其他幂次平均复合判断矩阵集成的性质。综上所述,需要对幂平均复合判断矩阵的一致性问题进一步研究,主要从以下几个方面进行讨论:(1)若专家群体判断矩阵均具有满意一致性,则其他类型的加权幂平均复合判断矩阵是否也具有满意一致性?(2)当判断矩阵满意一致时,幂平均的次数与一致性指标的关系如何?是否幂平均的次数越高,一致性越好?(3)判断矩阵的阶数对满意一致性的影响如何;(4)复合判断矩阵满意一致性比率关于专家权数灵敏性问题。
1 基本概念与理论
定义1设A=(aij)n×n(i,j=1,2,…,n)为判断矩阵,若
aij=aikakj,(i,j,k=1,2,…,n)
(1)
成立,称判断矩阵A是完全一致的。
定义2设A=(aij)n×n为判断矩阵,矩阵的抽象幂运算为
(2)
定义3设判断矩阵A=(aij)n×n,B=(bij)n×n的Hadmard积为C=A⊗B,其中,
cij=aijbij,(i,j=1,2,…,n)
(3)
定义4设判断矩阵A=(aij)n×n,B=(bij)n×n,矩阵的抽象加法运算为C=A⊕B,其中,
(4)
定义5称A=(aij)n×n为拟次序判断矩阵,若满足当i
(5)
定义7设判断矩阵A(h)(h=1,2,…,m),f(·)为正实数域上非负单调幂函数,加权幂平均(WPM)算子定义为

(6)
注1当s=1时,WPM算子即为加权算术平均(WAM)算子
(7)
注2当s=2时,WPM算子即为加权平方平均(WSM)算子
(8)
注3当s→0时,WPM算子即为加权几何平均(WGM)算子
(9)
注4当s=-1时,WPM算子即为加权调和平均(WHM)算子
(10)
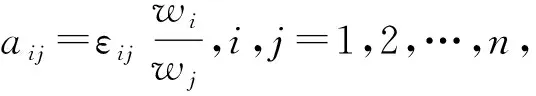

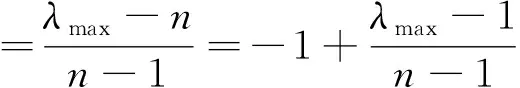
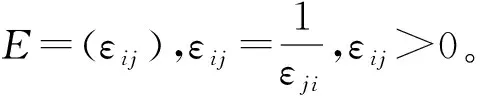
(11)


表1 随机生成矩阵的一致性指标值的均值
由矩阵的抽象加法“⊕”和乘法“⊗”运算的定义可知:运算具有可交换性、可结合性等优良性质;运算却不具备数乘可分配性和乘法对加法的可分配性。
性质1A⊗B=B⊗A。
性质2(A⊗B)s=As⊗Bs,s∈R。
性质3A⊗B⊗C=A⊗(B⊗C)=(A⊗B)⊗C。
性质4A⊕B=B⊕A。
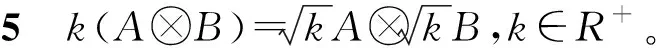
性质6A⊕B⊕C=A⊕(B⊕C)=(A⊕B)⊕C。
性质1~6的证明:A⊗B=C,B⊗A=G,cij=aijbij=bijaij=gij,∴C=G,性质1成立。

A⊗B⊗C=P,pij=aijbijcij=aij(bijcij)=(aijbij)cij,∴A⊗B⊗C=A⊗(B⊗C)=(A⊗B)⊗C,性质3成立。
∴A⊕B=B⊕A,性质4成立。
性质5成立。
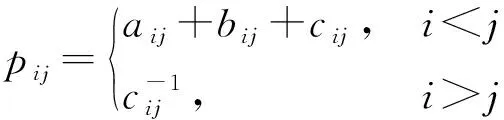
∴A⊕B⊕C=(A⊕B)⊕C=A⊕(B⊕C),性质6成立。
注5A⊗(B⊗C)≠(A⊗B)⊕(A⊗C)。
A⊗(B⊕C)=P=(pij)n×n
(A⊗B)⊕(A⊗B)=T=(Tij)n×n
∴pij≠tij。
A⊗(B⊕C)≠(A⊗B)⊕(A⊗C)。
2 主要结果
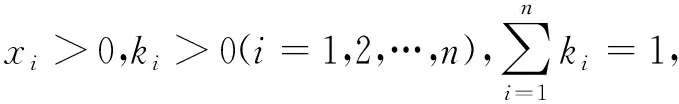
H≤G≤A≤S
(12)
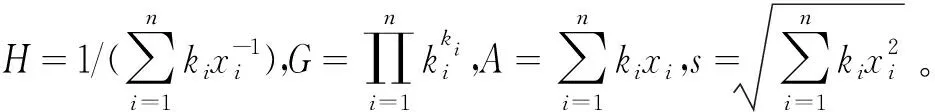

定理的证明:
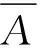

因为A(h)(h=1,2,…,m)是满意一致矩阵,从而有
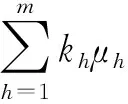

3 数值算例
设有四个专家针对四个指标分别进行评价得到拟次序判断矩阵A(h)(H=1,2,3,4),并给出各专家判断矩阵的权重向量以及一致性比率(见表2)。
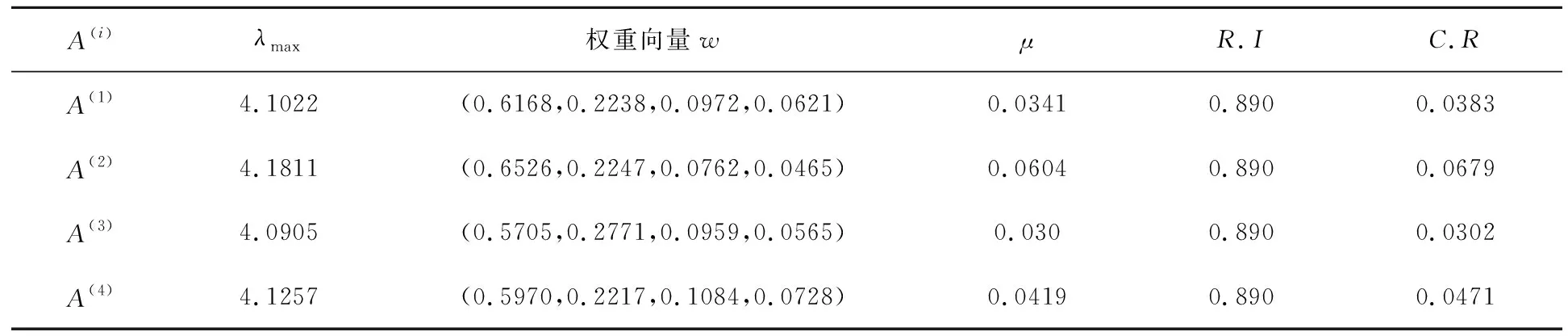
表2 专家判断矩阵的计算结果
依据一致性比率C.R<0.1,可知四个专家判断矩阵均通过一致性检验,是满意一致性矩阵。
(1)若假设四个专家中没有权威专家,不妨设权重为k1=k2=k3=k4=0.25。此时,计算得到的加权调和平均复合矩阵为
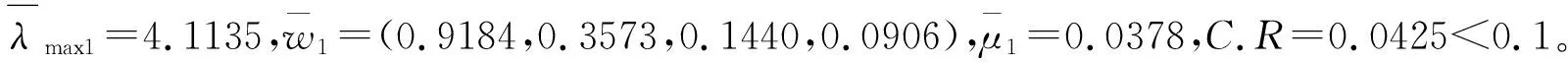
(2)若四位专家的权重有差异,不妨设k1=0.1,k2=0.2,k3=0.3,k4=0.4。经计算得到的加权调和平均复合矩阵为
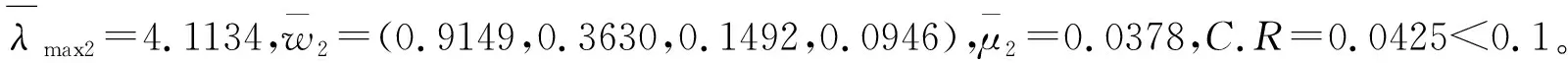
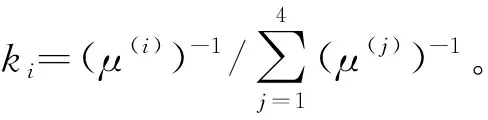
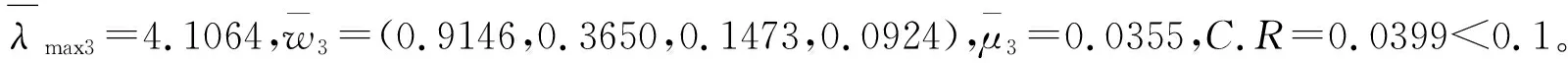
计算结果表明:在等权重、非等权重的情形下,所得加权调和幂平均复合判断矩阵均为满意一致性矩阵,一致性比率关于专家权重的扰动灵敏度较低。
利用上述四个专家判断矩阵,针对幂平均次数为s=1(加权算术平均)和s→0(加权几何平均)的两种情形下,分别计算出复合判断矩阵的一致性比率并与本文方法进行比较。从表3可以看出,三种幂平均复合判断矩阵具有近似的权重向量,均为满意一致矩阵,一致性指标值在0.0440附近,本文方法(s=-1)的一致性比率最小。

表3 幂平均复合判断矩阵的选择方法与结果比较
然而,其他幂平均的次数如何影响一致性比率未知,计算它们之间的变化规律(见图1)。
从图像上可以发现,四阶判断矩阵随着幂平均的次数的变化,一致性比率的变化关于次数s的图像呈凹函数关系,且具有以下特征:
(1)当s∈(-∞,-1.23)∪(1.23,+∞)时,C.R>0.1,即复合判断矩阵不是满意一致的;
(2)当s→0时,C.R→0, 此情形下的复合判断矩阵趋于完全一致矩阵;
(3)当s∈[-1.23,1.2]时,C.R<0.1复合判断矩阵为满意一致矩阵。采用专家判断矩阵的数据计算复合判断矩阵过程中,考虑不同的复合判断矩阵结构的三种情形下对一致性比率的影响:
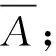
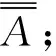
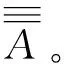
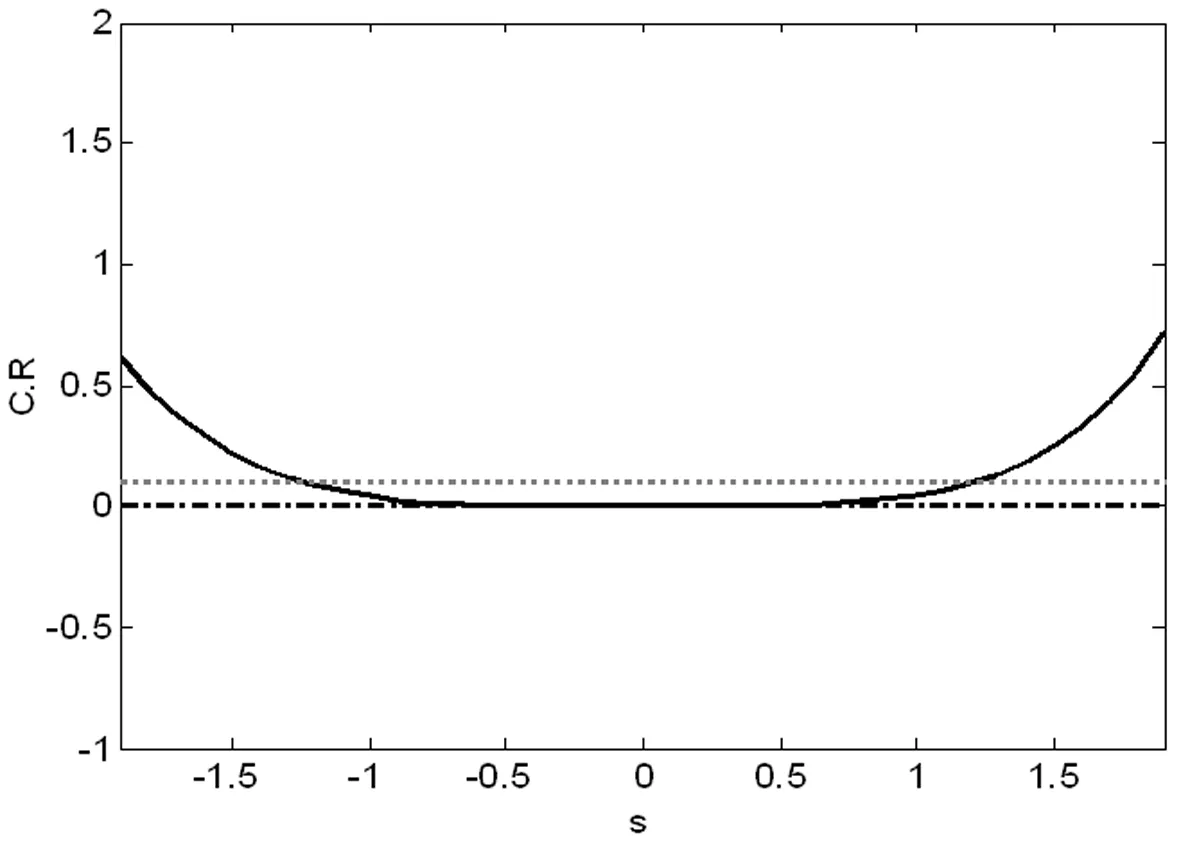
图1 幂平均的次数与一致性比率的关系(n=4)
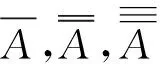


表4 调和平均复合判断矩阵的一致性比率
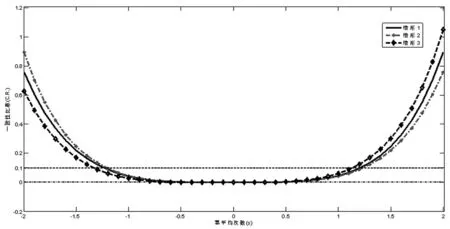
图2 三种情形下的调和平均的次数与复 合判断矩阵一致性比率的关系
当幂平均的次数改变时,三种情形下的这种相似性比较明显(见图2),从图形上看,当幂平均次数小于时,情形(2)的一致性较差,情形(3)的一致性最佳;而当幂平均次数大于1时,情形(3)的一致性反而最差,情形(2)的一致性表现的效果最佳。本文提出的方法即对判断矩阵中大于1的元素进行幂平均的效果介于两者之间,一致率的效果表现适中,本文方法所得复合判断矩阵的一致性比率相对比较稳定。
从判断矩阵的阶数来看,幂平均复合判断矩阵的一致性比率会随着阶数的升高呈下降趋势,即评价体系的指标数越多,经幂平均复合后的判断矩阵一致性程度效果越好。有趣的是,随着阶数的升高一致性比率关于幂平均的次数仍呈先减少后增加的趋势,且在当s→0时,复合判断矩阵趋于完全一致矩阵(见表5)。
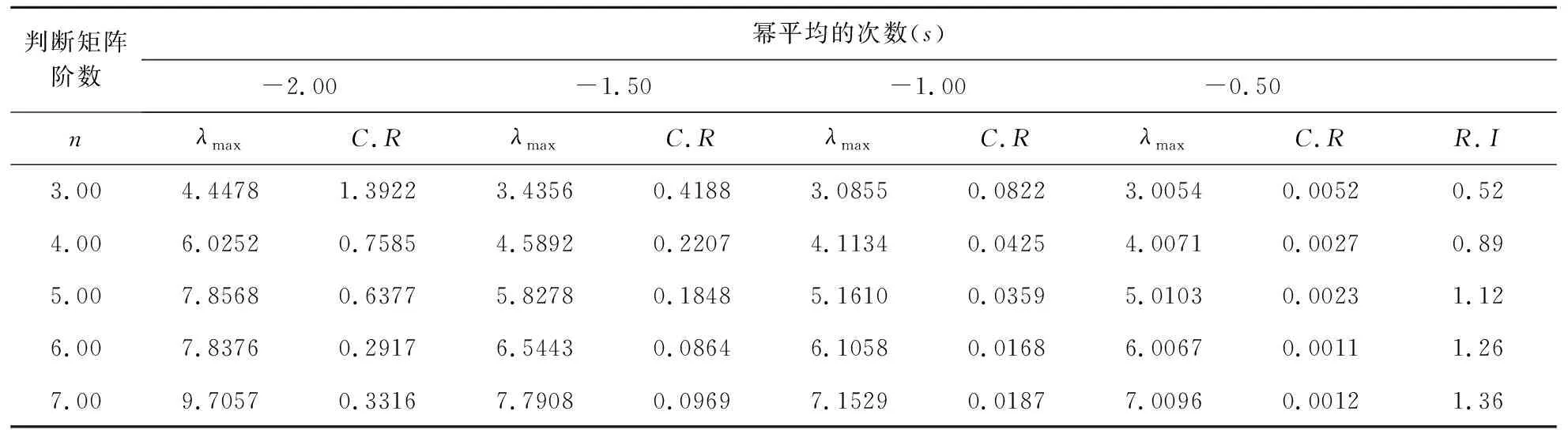
表5 幂平均次数、判断矩阵阶数对复合判断矩阵一致性比率的影响结果
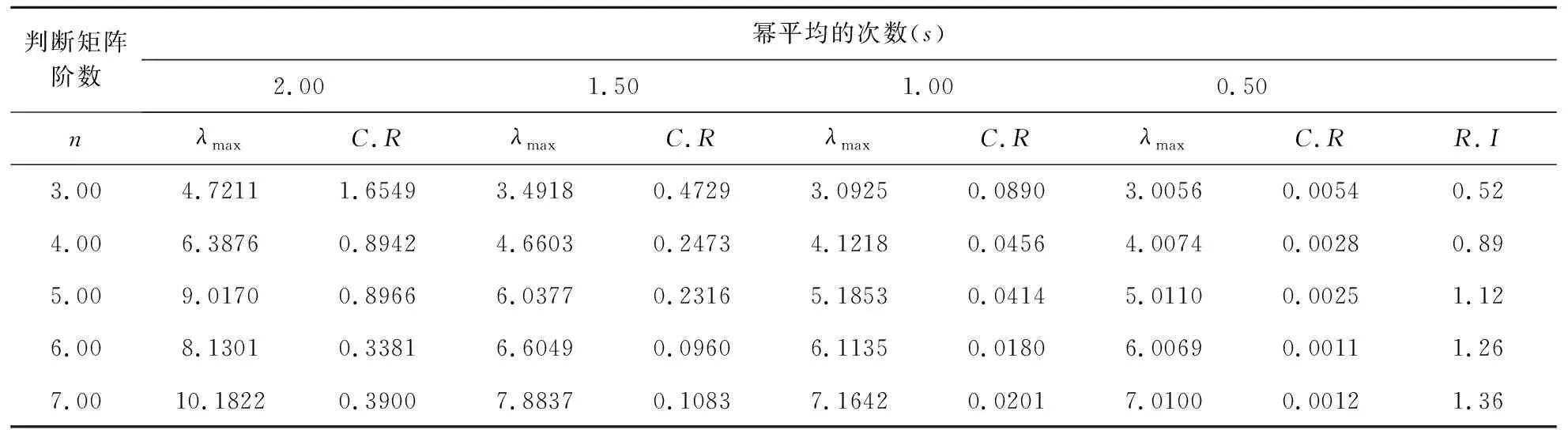
续表5
4 结束语
群体评价中专家判断矩阵的复合及其构成的复合判断矩阵一致性研究是十分有意义的。本文针对加权幂平均复合判断矩阵的一致性问题进行了研究和探索,结果表明:
(1)幂平均的次数会影响复合判断矩阵的一致性,幂平均的次数在有限区间内保证复合判断矩阵的满意一致性,有限区间长度同时依赖于判断矩阵的阶数与幂平均的次数,且一致性比率是关于幂平均次数的凹函数;当判断矩阵的阶数n=4时,复合后判断矩阵满意一致性的幂平均次数有限区间为[-1.23,1.2],随着阶数的升高,有限区间的区间长度会随之增加;
(2)判断矩阵的阶数越高,对专家给出判断矩阵的难度加大,然而随着判断矩阵阶数的升高,一致性比率会呈递减趋势,即专家的共识趋同;
(3)专家的权数对于一致性比率影响较小,即专家权数的灵敏度较低,给定权数扰动后不会影响复合判断矩阵的满意一致性。
然而,在判断矩阵阶数任意给定的一般情形下,尚未给出使得幂平均复合判断矩阵也为满意一致矩阵的有效区间。下一步的研究方向是进一步研究幂平均复合判断矩阵一致性问题的理论基础,分析复合判断矩阵的最优幂平均次数以及专家判断矩阵内部元素的波动性对复合判断矩阵一致性的影响机制,构建模型从而实现群体评价中的共识判断。
