需求可变性降低对均值CVaR约束销售努力决策库存系统的影响
2020-10-24禹海波唐中君
禹海波, 那 娜, 李 媛, 唐中君
(北京工业大学 经济与管理学院,北京 100124)
0 引言
市场不确定性的变化会影响到企业的利润和竞争力。随着产品生命周期缩短、顾客需求更加个性、产品研发困难等因素,企业面临的是可变性更加复杂的市场。例如,在2001年的第二季度,思科公司(Cisco)由于需求的快速减弱加上已签署的供应协议,使其花费了近25亿美元进行库存注销[1]。金宝汤(Campbell Soup)作为一家拥有148年历史的公司,其供应链的运作也曾经受到意外的需求高峰的严重影响[2]。由此可见,无论是需求的快速减弱还是意外高峰都会对企业的正常运作产生重要的影响。除此之外,需求的不确定性在医药行业、高科技行业中更加显著。例如,抗病毒流感药物达菲(Tamiflu)在2013年被淘汰,主要是因为需求意外地比前一年翻了一倍[3]。在高科技行业中,英特尔全球商品经理在受访中表示:“由于需求速度快和不可预测的变化以及技术产品的高周转率,导致业务供需管理极具挑战,降低需求可变性(例如进行市场调查)对公司有直接的积极影响。”产品周期缩短使需求预测更加困难,因为需要预测之前未投放市场的新产品。韩国最大的消费电子公司之一的物流规划总监表示:“大部分新产品在市场上是缺货的,理想情况下企业希望降低需求不确定性[4]。”因此,研究需求可变性降低对企业经营决策有重要的作用。目前随着技术的发展,有一些措施可以降低需求可变性。例如,在市场经济不同状态时,投放不同利润等级的产品,在市场经济繁荣时发展比较固定的客户等,这些措施在一定程度上都可以降低需求可变性;并且同一个产品在市场规模和市场状态不同时,它们的需求可变性也是不同的[5]。那么,如何有针对性的降低需求可变性是我们值得研究的问题。
常见的用于研究可变性对库存和供应链等复杂系统影响的方法有随机占优、可变序和均值保持变换。但从已获得文献来看,很少有文献对需求可变性的降低进行刻画,将之运用到库存系统决策问题中的文章就更为稀少。其中,用随机占优和可变序研究需求不确定性对库存决策及其成本(或利润)影响的文献相对较少,因为定量刻画市场需求可变性对库存决策和收益的影响是比较复杂的。Song[6]运用多可变序得到最小化成本库存系统的最优订货量和期望成本随机比较的充分条件,证明期望成本随可变性的增大而增大。Ridder等[7]通过三角概率分布给出,在一定条件下,期望成本随需求可变性增大而减少,这与直观的认识不同。禹海波[8,9]应用随机占优研究了需求可变性对库存系统的影响。但是,随机占优不太适用于一些较为复杂的库存决策问题。另一种定量刻画需求可变性对系统影响的方法是均值保持变换,但用均值保持变换研究随机变化对系统影响的文献比较少见。有一类文献是研究均值相等的变换,如Gerchak和Mossman[10]运用线性且均值相等的一类均值保持变换研究了需求可变性增加对最小化成本报童问题的影响。禹海波和王晓微[11]、禹海波和周端[12]通过均值保持变换来定量刻画决策者的过度自信水平,研究过度自信对库存系统和供应链的影响。另一类是研究均值可能不等或非线性的变换,如Levy[13,14]提出的一类均值可能不等的变换,Zhu和Wu[15]提出了一类非线性且均值相等的均值保持变换;但这两篇文献没有把变换应用到报童问题的库存决策中。
除需求可变性之外,决策者的风险偏好行为也会影响企业的收益。事实上,并非所有的决策者都是理性的,大部分人会采取保守的态度而选择规避风险,但也有部分激进投资者为更多的预期利润而追求风险。所以在研究需求可变性降低时,不仅要研究期望收益,还要研究风险对它的影响。对决策者来讲,可能存在风险中性,风险厌恶和风险追求这三情况,需求可变性的降低对它们的影响可能是不同的。因此,分别讨论需求可变性降低对不同风险偏好决策者的影响是十分必要的。
已有文献中研究风险偏好的测度主要有:期望效用函数、均值-方差、VaR、CVaR准则,但以上准则只能刻画决策者风险厌恶偏好,无法考虑多种风险偏好行为,并且均值-方差、VaR在计算上存在一定的劣势[16]。Gotoh和Takano[17]、Jammernegg和Kischka[18]提出混合条件风险价值概念(简称混合CVaR),能同时反映出决策者风险追求、风险中性和风险规避三种风险态度。Gotoh和Takano[17]、Jammernegg和Kischka[18]和禹海波[9]研究了混合CVaR约束下的库存模型,并且禹海波[9]证明了均值CVaR在一定条件下具有损失规避的特性。所以本文运用均值CVaR准则刻画零售商的风险偏好行为。
另外,随着经济技术的快速发展,产品的生命周期逐渐缩短,特别是时装、电子电器、软件技术等行业。如何在产品一开始投放市场时就取得大量销售业绩是企业必须要重视的问题。有关市场营销的报告表示:很多情况下,企业有效的销售努力行为可以扩大市场需求 ,比如设计产品在货架上的摆放、培训销售人员、定期做促销活动、加大广告投入等[19,20]。已有文献中有关需求依赖于销售努力的报童模型和供应链决策研究主要分为两大类。
第一类是基于风险中性下,研究报童模型或供应链销售努力、库存决策和协调契约问题。Pang等[21]分别研究加法和乘法需求模型下,由制造商,经销商和零售商组成的三级供应链的销售努力和库存决策问题。其它研究可参见Ma等[22]、Taylar[23],Cachon[24]等。第二类是研究报童模型或供应链同时受到销售努力和风险厌恶双重因素影响下的库存决策和协调问题。Chiu等[25]、许民利等[26]均研究了需求依赖销售努力时,风险厌恶供应链的最优订货和销售努力决策,以及TSR合同(Target Sales Rebate Contract)协调供应链的条件。Chernonog等[27]应用期望效用函数刻画零售商和供应商的风险,研究风险规避供应链下价格和销售努力双重决策问题。Suo等[28]基于收益共享和成本共担契约下,研究零售商损失规避对其销售努力决策的影响。禹海波[8]、代建生[29]均基于CVaR准则下,分别研究了销售努力和库存决策的风险厌恶报童模型和风险厌恶供应链回购契约问题。
综上所述,本文重点研究需求可变性的降低对不同风险偏好决策者的销售努力和库存决策的影响。与本文密切相关的两篇文献分别是禹海波[8]和禹海波[9]。禹海波[8]用最大化CVaR研究了风险厌恶和需求不确定性对销售努力和库存决策的影响,禹海波[9]研究了混合CVaR的随机单调性,并将其应用到库存系统中,得到需求可变性对最优订货量和最优期望效用的影响。但是,禹海波[9]这篇文献没有完全解决风险追求情形下需求可变性对系统最优期望影响的问题,也没有研究需求可变性降低对系统的影响。
本文将禹海波[8,9]进行推广,运用均值CVaR刻画零售商的风险偏好行为,并将Levy[13]提出的均值可能不等的变换应用到需求依赖销售努力且均值CVaR约束的库存系统中。首先,运用该变换来刻画需求可变性的降低(由其性质决定,详见注1),并研究它与传统方法—随机占优之间的关系(性质1),其次将该变换应用到需求依赖销售努力且均值CVaR约束的库存系统中,得到系统的库存决策、最优销售努力决策和最优期望效用(定理1),并证明关它们关于风险偏好系数的单调性以及降低需求可变性对期望效用的影响(定理2)。第三,针对风险中性、风险厌恶(最大化CVaR)和风险追求(最小化CVaR)这三种特殊情况得到相应的结果,并给出企业在库存决策和促销决策的管理启示(注12~注14)。
本文主要结构如下:第二部分运用Levy提出的变换(LMPT)刻画需求可变性的降低,研究它与随机占优之间的关系,并将该变换与广义TTT变换结合,特征刻画其随机单调性;第三部分将LMPT应用到需求依赖销售努力且均值CVaR约束下的库存系统中,研究其库存决策和最优销售努力决策,并得到它们关于风险偏好系数的单调性以及降低需求可变性对期望效用影响,并得到一些管理启示;第四部分分别研究降低需求可变性对风险中性、风险厌恶(最大化CVaR)和风险追求(最小化CVaR)三种偏好下最优期望效用的影响,并给出企业在库存决策和促销决策的管理启示;第五部分通过数值例子对上文的研究结果进行验证,并给出一些管理启示;第六部分进行总结,并指出值得进一步研究的问题。
1 LMPT的随机单调性
本文用Levy[13]提出的一类变换(LMPT)来刻画需求可变性的降低,因为该变换的方差和变异系数小于等于变换前的方差和变异系数,但该变换的均值与变换前不一定相等。它是Gerchak和Mossman均值保持变换[10](mean-preserving transformation, MPT)的推广。
本节研究该变换在不同随机序意义下的随机单调性以及它与随机占优之间的关系。

Levy[13]提出的变换(LMPT)具体如下
Xα,r=αX+(1-α)r
(1)
其中0<α≤1,r>0是实数,α表示需求可变性系数,r为代表无风险情形下实际的平均市场需求(Levy)[13]定义r为无风险投资利率)。
注1(i)给定参数α,当0<α≤1时,Var(Xα,r)=α2Var(X)≤Var(X),Cv(Xα,r)≤Cv(X)。即当0<α≤0时,该变换的方差和变异系数总会小于等于变换前的方差和变异系数。对应现实中企业家努力减少市场需求波动的情况。
(ii)当r>μX时,Xα,r的均值大于传统需求X的均值;当r=μX时,Xα,r的均值与传统需求X的均值相等;当r<μX时,Xα,r的均值小于传统需求X的均值。通常我们认为μX为市场稳定时的平均市场需求,当r>μX时,可以理解为市场繁荣时的平均市场需求;当r<μX时,可以理解为市场萎缩或金融危机时的平均市场需求。
因此,该变换(LMPT)Xα,r可刻画为:在市场状态不同时降低需求可变性后的平均市场需求。
注2(i)当α=1时,该变换(LMPT)Xα,r退化为传统的需求X;(ii)当r=μX时,该定义与Gerchak和Mossman[10],Zhu和Wu[15]的变换一致。(iii)Levy[13]和Levy[14]都没有将该变换应用到库存系统中。
记定义在区间[l1,0]和[l2,∞]上的随机变量X1和X2的累积分布函数分别为F1(·)和F2(·),表示l1与l2中较小的数。对于所有的t∈[l1∧l2,∞]定义如下2类函数:

根据禹海波[30](第三章55页)给出可变序和随机占优的定义。
定义1(i)如果X1和X2的累计分布函数之差的符号变换次数为1,即S(H1(·))=1,且符号序列为(+,-),则称X2按割准则序比X1大,记为X1≤cutX2。其中S(g(·))=k表示定义在区间[l1∧l2,∞]上函数g(·)的符号变换为k次(k=0,1,2,3,...),具体定义参见禹海波[30](第三章55页)。
(ii)如果H2(t)≥0对所有t∈[l1∧l2,∞]成立,则称X1在2阶随机占优意义下比X2大,记X1≥2-SDX2。
下面引理1给出随机占优和广义TTT变换之间的关系。广义TTT变换用于研究需求可变性对库存决策和最优利润(效用)的影响,见禹海波[30]。(A⟺B表示和B等价,A⟹B表示能推出)。

(i)E[X1-X2]≥0且X1≤cutX2⟹X1≥2-SDX2。


下面性质1给出对应不同参数α1,α2,0<α1<α2≤1对应的变换(LMPT)Xα1,r,Xα2,r的相关性质,给出它与随机占优和广义TTT变换之间的联系。
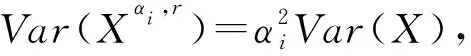
(i)当0<α1<α2≤1时,S(FXα2,r(·)-FXα1,r(·))=1,w.s.s(+,-),即Xα1,r≤cutXα2,r;
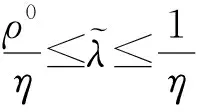
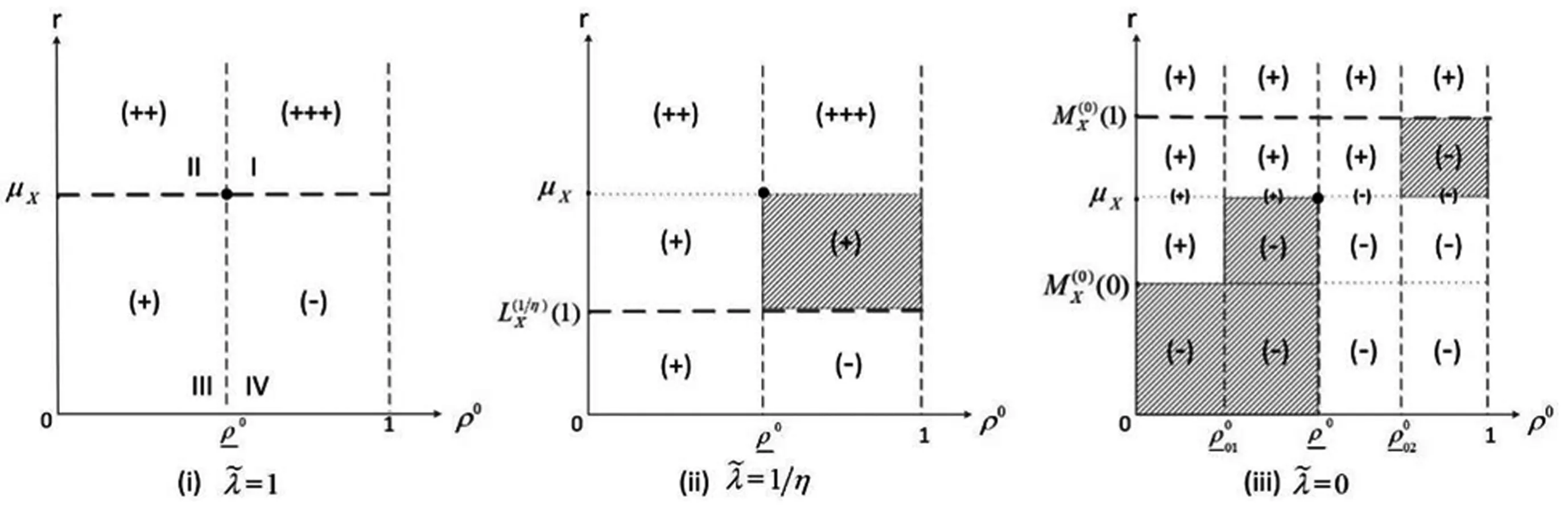
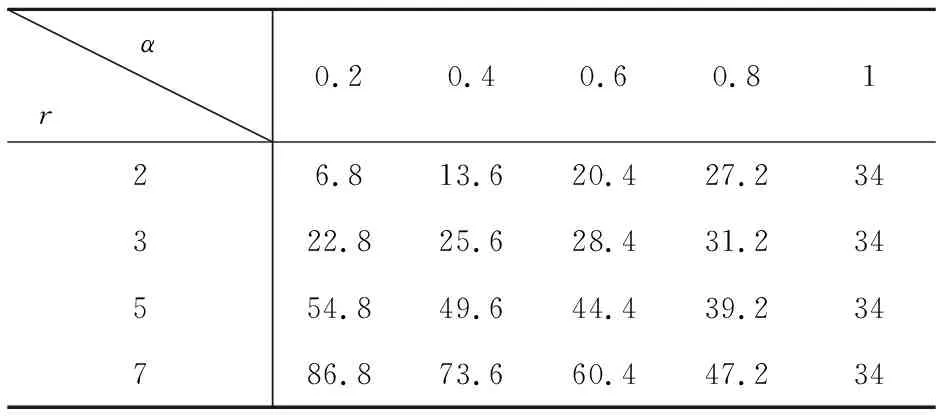
(ii)当0<α1<α2≤1,r≥μX时,Xα1,r≥2-SDXα2,r且Cv(Xα1,r) 注4若α1=1,α2=α,根据性质1可得该变换(LMPT)Xα,r与X(变换前后)的相关性质。在此条件下,性质1(ii)同禹海波[9,30],Stoyan[31]结论。 注5由性质1(iv)b)可知:在市场较为低迷或萎缩时,生产低利润产品的企业可以通过降低需求可变性(如信息共享或与其他企业合作[5],进而获得更高的利润;而生产高利润产品的企业可以通过增加需求的可变性来获得更高的利润(如把这些产品推向具有高度的可变性的市场)。 本节运用Levy[13]提出的变换(LMPT)建立需求函数,均值CVaR准则刻画零售商风险偏好行为,得到需求依赖销售努力的库存系统的最优订货量、最优期望效用和最优销售努力水平,之后进一步研究降低需求可变性和风险偏好对库存系统的影响。 考虑单周期生产单类产品的库存系统,假设市场需求d(e,Xα,r)是依赖销售努力水平e的随机变量,根据文献[23]和[24]可知,努力因素通常以加法和乘法两种形式影响需求。本文假定市场需求满足努力因素与随机因素的乘法形式,具体如下: d(e,Xα,r)=β(e)Xα,r (2) 其中β(e)是e的单调增函数,即β′(e)>0,意味着销售努力越大对应的市场需求就越大。Taylar[23]取β(e)=e,Xα,r满足式(1)。系统在周期开始前没有库存。在销售周期开始时,零售商决定以价格c向上游供应商订购该产品,订货量记为y。当需求的实现小于订货量y时,在销售周期结束时零售商以单位残值v处理剩余产品,0 假设零售商是风险偏好的,基于Gotoh和Takano[17]、Jammernegg和Kischka[18]提出的混合CVaR概念及禹海波[9]给出的混合CVaR与均值CVaR的等价性,本文定义并运用均值CVaR准则来刻画零售商的风险偏好行为。 针对大数据处理的服务架构搭建,要保证架构的稳定性,和容错率较高,在大数据分析技术中使用集群搭建,在不同的服务之间分布式搭建,合理的应用现有的资源,将资源利用率最大化。 (3) (4) (5) 这里x+=max{x,0}。 为方便本文计算,下面引理2给出混合CVaR与均值CVaR的等价性。 (6) (7) 注7(i)均值CVaR准则和均值-方差、VaR准则之间,测度具有一致性[34],但均值-方差、VaR准则只适用于正态分布,而均值CVaR准则可用于一般分布。均值-CVaR较均值-方差、VaR而言,计算结果更优。(ii)均值-CVaR有与二阶随机占优一致的随机单调性[9]。 零售商的目标是决策订货量y和销售努力水平e使其期望效用达到最大,则零售商的目标函数如下: (8) 其中,Π(y,d(e,Xα,r)) =pmin{y,d(e,Xα,r)}+ v·(y-d(e,Xα,r))+-cy (9) 结合式(6)和式(7),问题(8)可等价为如下两种形式: (10) (11) 下面定理1给出问题(8)系统的最优订货量、最优期望效用和最优销售努力水平。 定理1考虑问题(8),需求函数满足式(2)。对任意0<α≤1,则: (i)给定销售努力水平e(e>0),系统的最优订货量为: (12) (13) (ii)给定销售努力水平e(e>0),系统的最优期望效用为: (14) (15) (16) (17) (18) (19) (20) 定理2考虑由式(8)给出的问题,需求函数满足式(2)。对任意0<α≤1,则: 表1 最优订货量关于α的单调性↓ 表2 最优期望效用和最优销售努力水平关于α的单调性 本节研究降低需求可变性对最优期望效用的影响,分别考虑零售商为风险中性、风险厌恶和风险追求情形时,不同地区企业降低需求可变性对期望效用的影响。 (21) (22) (i)a)当r≥μX时,Δπ*(α,r,ρ0,1)是关于α的单调减函数。 b)当r<μX,存在ρ0∈(0,1), 当ρ0∈(0,ρ0)时,Δπ*(α,r,ρ0,1)是关于α的单调减函数,当ρ0∈(ρ0,1),Δπ*(α,r,ρ0,1)是关于α的单调增函数。 (ii)当r≥μX时,Δπ*(α,r,ρ0,1)是关于p的单调增函数。 (iii)Δπ*(α,r,ρ0,1)是关于r的单调增函数。 注12结合推论1分析企业降低需求可变性对期望效用的影响(对应图2(i))。根据Schweitzer和Cachon[35]对高利润产品和低利润产品的定义,我们划分:满足ρ0>ρ0为高利润产品,如奢侈品、高档手机、空凋等;满足ρ0<ρ0为低利润产品,如面包,本子等。 结合图2(i),推论1表明:当零售商为风险中性时,会做出理性决策。当市场比较繁荣、乐观时,无论是高利润产品还是低利润产品,企业通过降低需求可变性都会带来更多的利润,并且高利润产品效果更显著;而在市场较为低迷、萎缩时,针对低利润产品,企业降低需求可变性的措施对利润有积极影响,而对高利润产品来说,企业采取降低需求可变性的措施反而会对利润产生消极影响。例如,当金宝汤公司受到意外的需求高峰前,能够针对繁荣的市场采取一定的措施(与其他企业合作、共享信息等措施)来降低需求可变性,则在一定程度上能够有效的规避损失,获得更多的利润。 结合图2(ii)和(i)发现,此时零售商可能会在实际上损失利益的决策区域,采取降低需求可变性的措施(如图2(ii)中阴影部分),由此失误会导致企业损失一定的利益。比如当市场萎缩时,企业却采取合作或共享信息等方式去降低需求可变性,这样会进一步导致企业失利。因此,建议企业对市场经济的实际水平调研过后再决定是否进行需求可变性降低。 c)当r=μX时,存在ρ0∈(0,1),当ρ0∈(0,ρ0)时,Δπ*(α,r,ρ0,0)是关于α的单调减函数;当ρ0∈(ρ0,1)时,Δπ*(α,r,ρ0,0)是关于α的单调增函数。 (ii)Δπ*(α,r,ρ0,0)是关于r的单调增函数。 结合图2(iii)和图2(i)发现,此时零售商可能没有在实际获利的决策区域进行需求可变性的降低(如图2(iii)中阴影部分),由此失误会导致企业失去一定的获利机会。例如,在市场繁荣时,金宝汤公司没有意识到可以通过采取降低需求可变性的措施来得到更多的获利机会。因此,建议零售商可以在市场繁荣、乐观时通过信息共享,与其他企业合作等方式来降低需求可变性。 图2 降低需求可变性对期望效用的影响((+)代表积极影响,(-)代表消极影响)((+)或(-)个数越多代表影响程度越深) 本节给出特殊的例子,基于上文的LMPT,研究需求可变性降低对系统的影响。 表3 当时,最优期望效用的比较(η=0.2) αr0.20.40.60.81225.330.635.941.246.6341.342.643.945.246.6573.366.659.953.246.67105.390.675.961.246.6 αr0.20.40.60.8126.813.620.427.234322.825.628.431.234554.849.644.439.234786.873.660.447.234 本文运用Levy(1977)提出的变换(LMPT),首先给出该变换的相关性质,特征刻画该变换与广义TTT变换和随机占优之间的关系。之后,进一步将该变换应用到需求依赖销售努力且均值CVaR约束的库存系统中,研究其库存决策和最优销售努力决策,并用该变换来定量刻画需求可变性降低,研究对最优决策和最优期望效用的影响,以及风险偏好对系统影响的充分条件。最后通过数值例子研究零售商风险偏好对期望效用的影响,并得到一些管理启示。值得进一步研究的问题包括:1)将广义均值保持变换的应用推广到供应链系统中,讨论有多个决策者的库存决策及优化问题。2)广义均值保持变换的应用推广到供应链系统中,研究供应链契约协调问题。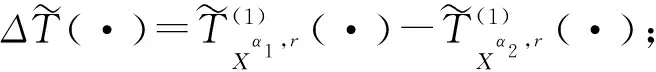

2 需求依赖销售努力且均值CVaR约束的库存系统

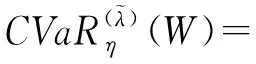




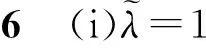











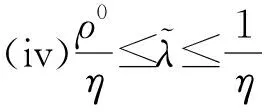

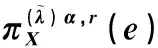


3 降低需求可变性对期望效用的影响

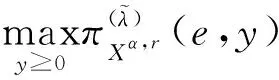





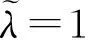











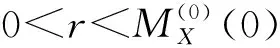

4 数值例子




5 小结
