兼顾成本与时间保证率的泊位及岸桥协同调度优化
2020-10-24宋云婷
宋云婷, 王 诺, 吴 暖
(大连海事大学 交通运输工程学院,辽宁 大连 116026)
0 引言
泊位和岸桥是集装箱码头最重要的资源,恰当合理地对这些资源进行协同调度,可以有效降低生产成本,提高企业管理水平。在合理选择泊位的基础上,采取尽可能地利用相邻泊位的岸桥协同作业,以便最大限度地减少岸桥的投入数量,降低码头作业成本便是其中一种重要的调度策略。研究这一泊位及岸桥协同调度方案的制定过程,构建相应的优化模型并设计有效的计算方法,对于港口生产的科学管理具有重要的现实意义。
目前,关于集装箱码头装卸调度的优化已有较多成果,如针对码头集卡与岸桥的协调调度问题,建立船舶在港时间最短、码头生产成本最小的优化模型[1~3];利用混合交叉作业方法与同步优化技术,建立集成调度优化模型等[4];针对泊位偏离和岸桥工作损失建立集装箱港口泊位和岸桥的混合整数线性规划模型等[5]。上述研究都有一个共同的前提,即无论船舶离港的时间是否紧急,无论需要装卸的箱量是否较多,都以船舶在港作业时间最短为优化目标[6~10],对于集装箱班轮而言,按照船期表规定的时间在港口完成装卸作业是其运行的基本性质,但对于如何结合泊位计划寻求岸桥开工数量以合理放缓作业速度的优化,则有待深入研究。
关于多目标问题的求解方法,也有诸多成果[11~13]。由于泊位分配、岸桥调度等属于NP-hard问题,因而通常利用优化算法求解[14~18]。为解决同时兼顾船舶靠泊位置和不同时刻岸桥工作状态问题,有的学者结合局部搜索算法对遗传算法进行了改进[19],采用两阶段启发式算法有效提高求解效率;针对计划期内泊位的状态和岸桥的同步调度相互关联的反馈关系设计嵌入启发式规则的遗传算法对其进行求解[20],但对于连续型泊位下泊位及岸桥协同调度的多目标求解问题还需要进行相应的改进和深化。
关于从Pareto解集中选择合理方案的问题,有的研究结合决策者的偏好[21~25]在求解过程中嵌入向量评价微粒群算法[26],或者以Pareto最优解和任何其它解冲突的大小进行排序[27],通过对双层规划上下层的协商寻求满意解以及建立指标评价体系[28,29]进行打分遴选,计算各Pareto非劣解相对于不同目标函数偏向度对Pareto非劣解进行量化评价[30]等等。但有关Pareto非劣解的寻优方法在港口管理中并未见到具体应用。
针对以上诸多问题,本文结合港口生产的实际特点,提出了新的优化思路,其主要的创新点及贡献是:①根据集装箱班轮按计划到离港的运行特点,引入集装箱班轮按计划离港保证率的概念,定量分析集装箱班轮在规定时间内完成装卸作业的概率;②以班轮按计划离港的保证率最大和码头装卸作业成本最低为目标建立多目标优化模型,采用带精英策略非支配排序的遗传算法求解,在此基础上以嵌入叠加式局部搜索算法解决相邻作业船舶共享使用岸桥问题,得到泊位及岸桥协同调度的Pareto解集;③利用“性价比”的方法对Pareto非劣解进行分析,确定既能满足集装箱班轮按计划离港的要求,又能够降低港口作业成本的最优方案,解决了在Pareto非劣解集中寻优的问题。最后,通过对大连港集装箱码头真实案例的分析,验证了本文优化模型的合理性和计算方法的有效性。
1 模型构建
1.1 模型假设
根据集装箱班轮靠泊的特点,本文采用连续型泊位的“柔性”分配方法,即沿码头岸线依次安排船舶靠泊。为简化起见,需做如下假设:①码头各泊位水深能够满足所有到港船舶要求;②船舶装卸效率与参与装卸的岸桥数成正比,即岸桥的单台作业效率不因岸桥数量的增加而改变;③允许岸桥在作业过程中移至其他船舶进行作业;④忽略岸桥移动过程的成本。
1.2 符号定义
(1)参数
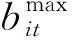
(2)决策变量
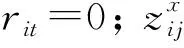
1.3 目标函数
为计算船舶按计划离港的保证率,首先需建立有关概念。
定义在正常装卸速度下,集装箱班轮能够在规定时间内完成装卸作业并按计划驶离港口的概率为船舶按时完成作业保证率。
设船舶i在港接受服务时间的概率服从爱尔朗分布,则集装箱班轮的按计划离港的保证率可表示为:
(1)
式中,T代表船公司与港方约定的船舶在港服务时间,μi代表船舶i的平均装卸效率,其取值由岸桥的单机作业效率和配置数量决定。
由以上分析,建立优化模型如下:
目标函数1:要求到港船舶能够按计划离港的平均保证率最大,即:
(2)
式中,P为所有到港船舶按计划离港的平均保证率,s为船舶数量。
目标函数2:要求码头装卸成本最低,即:
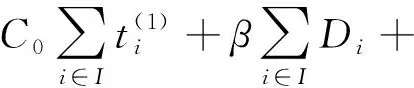
(3)
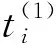
1.4 约束条件
Pi≥Pmin
(4)
(5)
(6)
(7)
(8)
(9)
(10)
上式中,式(4)表示任意船舶按计划离港保证率均需满足最低保证率要求;式(5)表示任意时刻作业的岸桥数不得超过港口配备的岸桥总数量;式(6)表示任意时刻所有靠泊船舶不得超过码头岸线范围;式(7)表示为每艘船舶配备的岸桥数量不能超过其可配备的最大岸桥数量;式(8)~(10)表示任意两艘船舶在停靠时间和停靠位置上不能发生冲突。
2 算法设计
对于多目标优化问题,需要找出解空间的Pareto边界供决策者选择。在算法选择时,由于带精英策略非支配排序的遗传算法(non-dominated sorted genetic algorithm-II, NSGA-II)具有隐含的并行性、随机性和高度鲁棒性特点,因而在多目标求解问题中具有较广的应用。但对于本文问题,为达到降低成本的目的,可允许岸桥在作业过程中在相邻船舶间协同使用,即在满足某一船舶能按时完成装卸作业的前提下,允许配备给该船舶的部分岸桥可中途转移至相邻船舶继续作业,这一调度策略大大增加了求解的复杂性。对此,本文专门设计了叠加式局部搜索算法,并将其嵌入NSGA-Ⅱ算法中。计算时,以遗传算法确定船舶的靠泊顺序与岸桥配置数量,以叠加式局部搜索算法对岸桥进行协同调度,两者不断交叉反馈推动计算进程,最终得到满足优化问题的Pareto解集。
2.1 嵌入叠加式局部搜索算法的NSGA-Ⅱ算法设计
2.1.1 染色体编码
采用十进制编码方式对染色体进行编码,设染色体长度为2s,第1到s位染色体代表船舶1到船舶s的靠泊顺序,第s+1位到2s位染色体代表船舶1到船舶s配置的岸桥数目。例如,当靠泊船舶为5艘时,染色体编码方式见图1。

图1 染色体编码方式
为保证种群的多样性,采用随机生成种群的方法,从第1到第s位染色体为1到s的随机整数序列,即船舶1到船舶s的靠泊顺序;第s+1到第2s位染色体为从船舶可配置的最小岸桥数到最大岸桥数之间的随机整数,即船舶1到船舶s配置的岸桥数量。
2.1.2 适应度函数
由于本文是解决多目标优化问题,因此个体的适应度值可通过个体的目标函数值比较得到。首先将种群中个体对目标函数值的表现进行排序,得到可行解的排序序列Xj,根据排序序列得到个体的排序号Ri(Xj),并通过式(11)~(12)可得到个体的适应度函数值,即:
(11)
(12)
式中,N为种群中个体数量,n为目标函数数量。
2.1.3 遗传操作
选择操作采用轮盘赌选择算子。交叉操作采用部分匹配交叉,即在染色体的第1至s位基因随机生成两个交叉点,把两个交叉点之间的基因序列插入对方染色体的第1个基因之前,然后将交叉段基因与原染色体基因相比较,再依次去除交叉段基因中相同的基因,将第s+1至2s位基因按照与前s位基因的对应关系重新排序,交叉过程见图2。
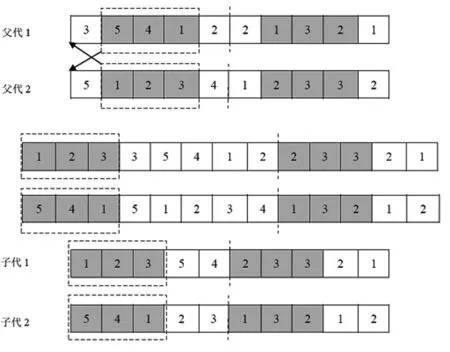
图2 染色体交叉过程
变异操作采用逆转变异法,分别对染色体的前后两段基因进行变异,以Pm为变异概率,在染色体的1至s位基因和s+1至2s位基因中分别随机生成2个位点,将2点之间的基因反转插入,产生新一代种群,变异过程见图3。

图3 染色体变异过程
2.1.4 叠加式局部搜索算法设计
所谓叠加式局部搜索,是指在局部搜索时,不断叠加前程搜索已完成的结果,在此基础上再拓展搜索范围循序进行。由于已有算法无法实现在作业中的岸桥从一艘船舶转移至另一艘船舶继续作业的调度方式,不能连续记录岸桥的工作和转移所需的时间,因此需要嵌入叠加式局部搜索予以解决。这一算法的核心思想是:当船舶i靠泊后,首先根据染色体编码确定船舶i的靠泊位置和初始配备岸桥数量,分析其相邻正在作业船舶的岸桥情况,以最低保证率和岸桥移动距离两方面判断是否采用协同调配策略:若能满足上述要求,则生成岸桥协同调配方案,确定船舶i的岸桥配备编号,记录对应的起止作业时间,同时更新受影响船舶的调度计划;若不满足,则依据染色体编码,在未参与作业的岸桥中确定新的调配方案。
2.1.5 算法步骤
以上算法的具体步骤如下:
Step1根据染色体编码规则生成染色体,得到初始的船舶靠泊顺序和岸桥配置数量;
Step2进行叠加式局部搜索,从确定的靠泊顺序(I1,I2,I3,…,Is)中选取首个待靠泊船舶,令i=Is;
Step3判断剩余岸线长度是否大于船舶i的船长。若是,令船舶i的靠泊位置距离前一艘停靠船舶舶船尾的所在位置向右l0米处;若否,令船舶i的靠泊位置距离码头岸线起始端安全距离l0米处,即yi=l0;
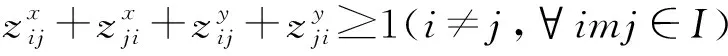
Step5令船舶i的靠泊时间延迟至冲突船舶j离港时间安全时间t0小时后,转Step4;
Step6判断船舶i需要配置的岸桥数目是否超过最大岸桥数目的限制。若是,进入Step7;否则,转Step8;
Step7按染色体生成规则重新生成新染色体,转Step2;
Step8判断船舶i和船舶i-1之间能否共用岸桥。若是,生成共用岸桥调度计划,并调整受影响船舶的调度计划;否则,生成船舶i的调度计划;
Step9判断船舶i是否为整个靠泊序列中的最后一艘船,即判断i Step10输出该靠泊船舶序列的作业调度计划,叠加式局部搜索结束; Step11根据所得作业调度计划,依据目标函数计算船舶序列的平均按计划离港保证率和作业成本; Step12根据目标函数值筛选初始非劣解集; Step13根据个体的非劣解水平进行非支配排序生成不同序值和前端,并计算同一前端不同个体之间的拥挤距离; Step14依据遗传操作规则进行染色体的选择、交叉及变异,同一前端中序值小、拥挤距离大的个体将优先被选择,获得子代B; Step15将父代A和子代B种群进行合并,重新进行非支配排序和拥挤距离的计算; Step16利用修剪函数对合并后的种群进行修剪,修剪规则为序值小拥挤距离大的个体予以保留,得到个体数等于种群大小的新种群C; Step17判断是否满足最大迭代次数要求。若不满足,转Step2; Step18筛选出最终非劣解集,得到Pareto解集,结束。 由多目标优化模型可知,在提高按计划离港保证率和降低作业成本之间要进行两全的选择,在这一对矛盾中不能有偏倚,需要在按计划离港保证率最大和作业成本最低的两个优化目标之间寻找一个平衡点,即寻求各目标均能接受即偏向最小的解,本文利用分析Pareto前沿性价比的方法选择其最优方案。所谓性价比量化方法的基本思想是,根据Pareto前沿的几何分布特点,其几何变化率分别相对于两个优化目标最灵敏的交点所对应的解即为无偏向的最优解[30](图4)。 图4 Pareto前沿各点平均变率的几何关系图(min-max模型) 基于上述思路,设J为Pareto解集的个数,可由小至大依次排列进行编号,P(j)表示第j个Pareto解的平均船舶按计划离港保证率,j∈{1,2,…,J};C(j)表示第j个Pareto解的平均装卸作业成本,j∈{2,3,…,J},则上述两目标的平均变化率为: (13) (14) (15) (16) (17) (18) 在此基础上,可得到相对于各目标的灵敏比: (19) (20) 为方便比较,需对上述结果进行无量纲化处理,具体表达式为: (21) 设灵敏比无量纲化差值的绝对值为Δε,有 (22) 式中符号意义同上。 由以上分析可知,灵敏比差值绝对值的最小值(Δε)min即为所对应的Pareto解即为所寻求的最优方案,即: (Δε)min=min{Δε(1),Δε(2),…,Δε(J)} (23) 式中符号意义同上。 现以大连港集装箱码头2010年11月16日实际生产的调度过程为背景。由现场调度记录,当时共有10艘班轮先后循序到港,各班轮的平均装卸箱量为341TEU,具体信息见表1。该码头岸线总长796m,配备有8台岸桥。由统计分析知,大连港集装箱班轮在港服务的时间服从8阶爱尔朗分布,班轮在港服务时间约定为16小时,要求任意1艘班轮按计划离港的保证率不低于80%。 根据集装箱码头的装卸工艺,装卸设备是以岸桥为核心,与场桥和集卡等按比例进行编组。由作业现场调查统计,岸桥、场桥和集卡按表2配备,当单船装卸量较少时,按下限值配备;反之按上限值配备。码头作业成本[27]见表3。 表1 到港船舶信息 表2 岸桥、场桥、集卡编组配置 表3 效率、成本的取值 利用前面建立的基于叠加式局部搜索的遗传算法,采用MATLAB编程,运算在P4CPU、内存2G、主频2.81HZ的环境下进行,取种群数量N=50,交叉概率Pc=0.5,变异概率Pm=0.1,最终得到12个满足最低保证率要求的Pareto非劣解(见图5)。由式(13)~(23),得到各非劣解对应的灵敏比无量纲化差值的绝对值(见表4、图6)。由式(23)求得(Δε(j))min=Δε(7),即图5中最小值的7#(亦即图6中的7#)所对应的方案为最优。由表4可见,Pareto非劣解集中7#方案完成作业的平均保证率达到90.27%,比保证率最低的1#方案高出达5.01%,而作业成本仅增加0.34%,综合结果最优。 按照方案7#,其作业计划具体为:当船舶1靠泊时,安排1#岸桥投入作业;当船舶2靠泊时,3#、4#岸桥投入作业;当船舶3靠泊时,4#岸桥由船舶2转至船舶3协同作业;当船舶4靠泊时,5#、6#、7#岸桥投入作业;当船舶5靠泊时,1#岸桥协同作业、2#岸桥投入作业;当船舶6靠泊时,2#岸桥协同作业;当船舶7靠泊时,4#、5#岸桥协同作业;当船舶8靠泊时,7#岸桥协同作业;当船舶9靠泊时,4#岸桥协同作业;船舶10靠泊时,1#岸桥协同作业(见图7),整个过程采取协同作业方式,自始至终只开动了8台岸桥中的7台作业,保留1台处于停产状态。与港口未优化前调度方案的对比可知,在满足所有船舶按计划离港保证率均大于80%的前提下,通过压缩岸桥的配置数量,使得港口装卸作业成本降低了1.04%(表5)。 图5 多目标优化模型的Pareto非劣解集 表4 Pareto解集对应的参数表 图6 灵敏比无量纲化差值的绝对值与作业成本的变化曲线注:括号中数字为与图5对应的Pareto解集编号 图7 泊位分配及作业安排示意图 表5 未采取协同策略的作业计划与7#方案优化效果对照表 本文解决的是泊位及岸桥的协同调度问题,即在合理选择泊位的基础上,以保证按规定时间完成装卸作业为前提,采用对相邻靠泊船舶的作业岸桥协同支援的方式,最大限度地减少岸桥等设备的投入数量、降低了码头作业成本。与以往研究的泊位及岸桥的常规调度问题相比,本文同时考虑了集装箱班轮按计划离港的要求和码头作业成本最低两个目标,结合泊位计划寻求岸桥协同调度的最佳配置和作业速度,因而大大增加了问题的复杂性。 本文引入按计划离港保证率的概念,以到港船舶按计划离港保证率最大和码头作业成本最低为目标,构建了泊位及岸桥协同调度的多目标优化模型。为求解岸桥协同调度问题,采用嵌入叠加式局部搜索算法的NSGAcvⅡ算法,以遗传算法决定船舶的靠泊顺序与岸桥配置数量;依据生成的靠泊顺序和岸桥数量,利用叠加式局部搜索方法,经过相互交叉反馈运算,得到了以目标函数进行非支配排序生成的Pareto非劣解。在此基础上,根据Pareto前沿的几何分布特点,以性价比的概念得到对应两个优化目标偏向最小的最优解。最后,以大连港集装箱码头的真实案例进行分析,结果显示,以本文的优化思路得到的泊位及岸桥协同调度计划与港口实际调度计划相比,在所有船舶按时离港的保证率均大于80%的前提下,通过压缩岸桥参与生产的配置数量,可使港口装卸作业成本降低1.04%,验证了文中提出的优化思路和算法在解决实际问题中的有效性,取得了既满足船舶按时完成作业要求,又降低港口作业成本的效果。 研究中,本文将集装箱班轮在港作业时间设为常量,实际中,还存在部分班轮公司要求船舶在港作业时间不同甚至会出现临时变化的情况,如何在更为复杂的情况下寻求协同调度的优化方案,是下一步需要研究的课题。2.2 Pareto最优解的选择

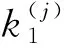
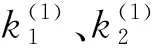
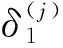
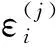
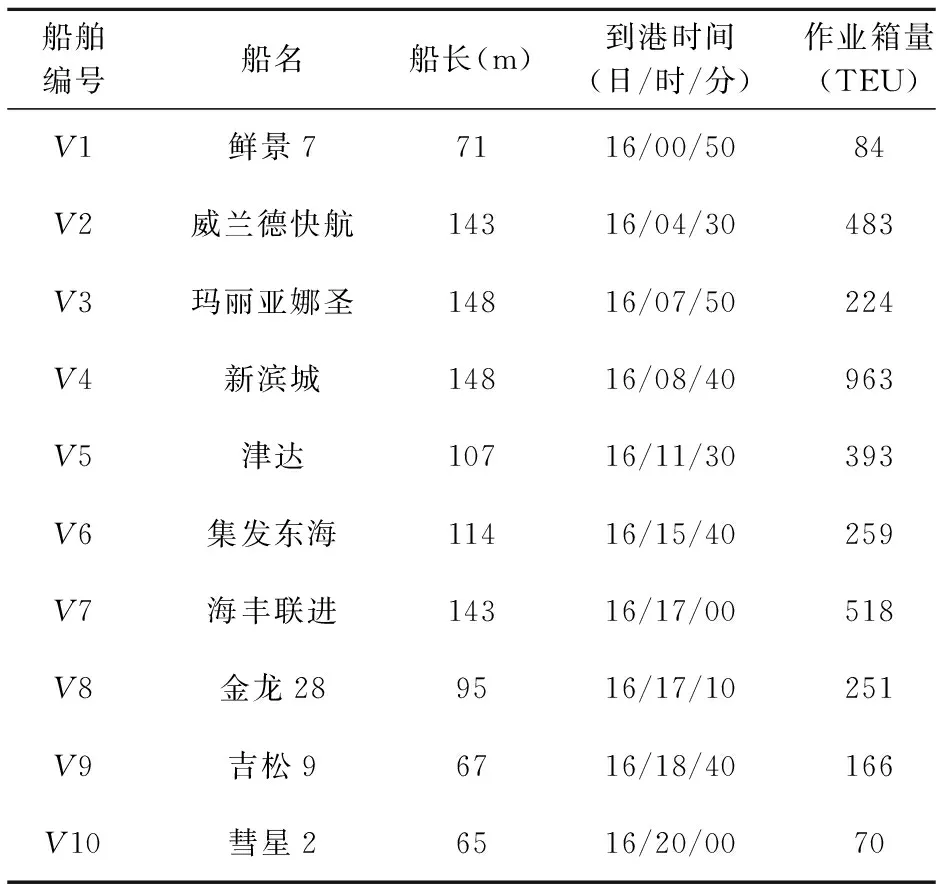
3 算例分析
3.1 基本数据
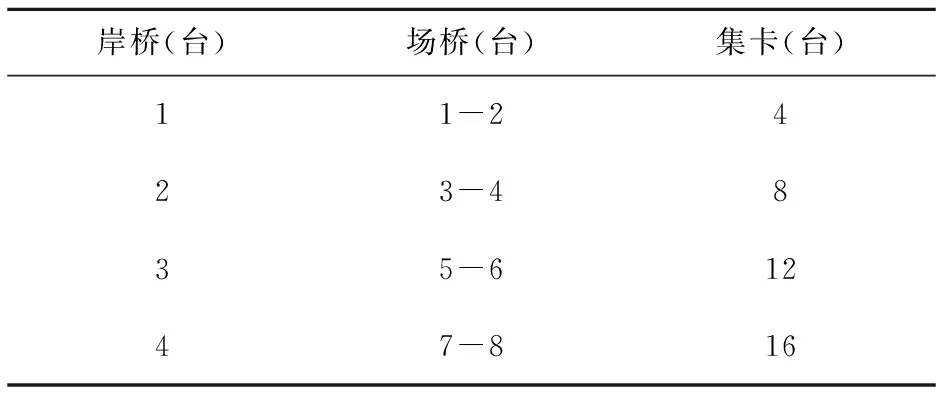

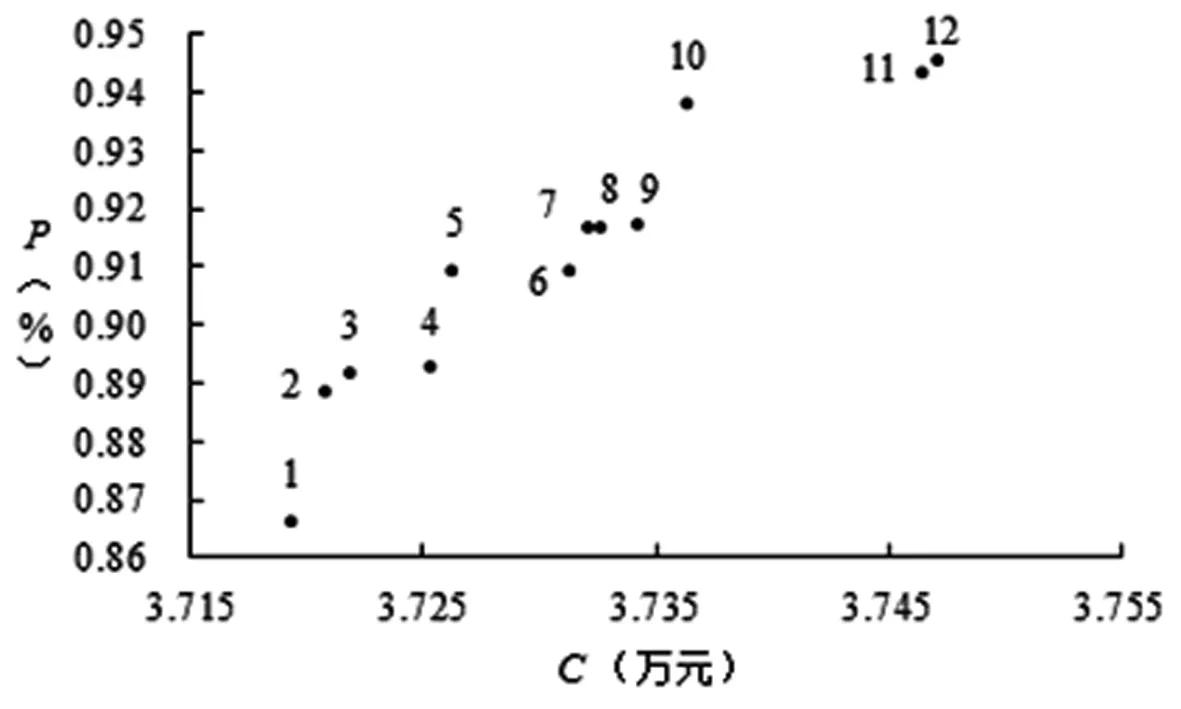
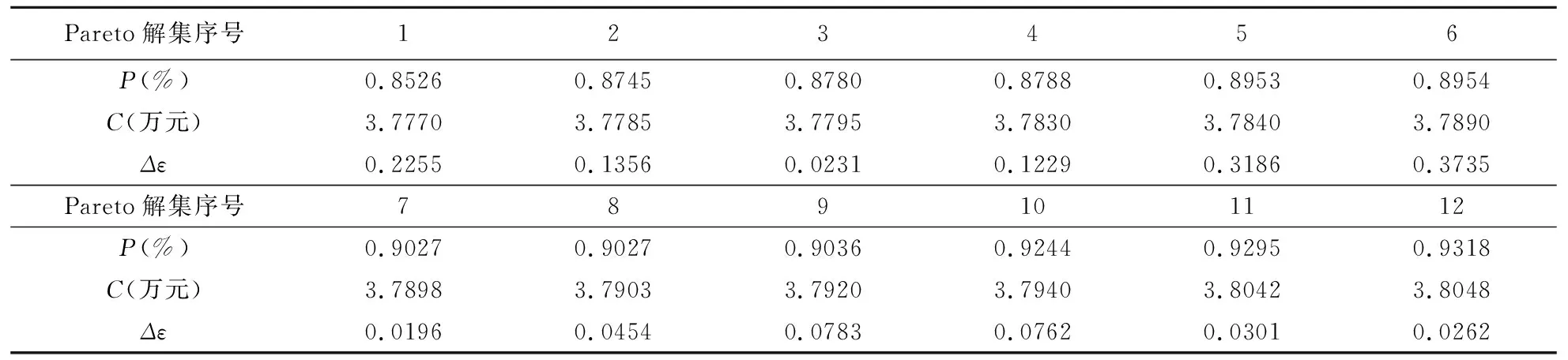
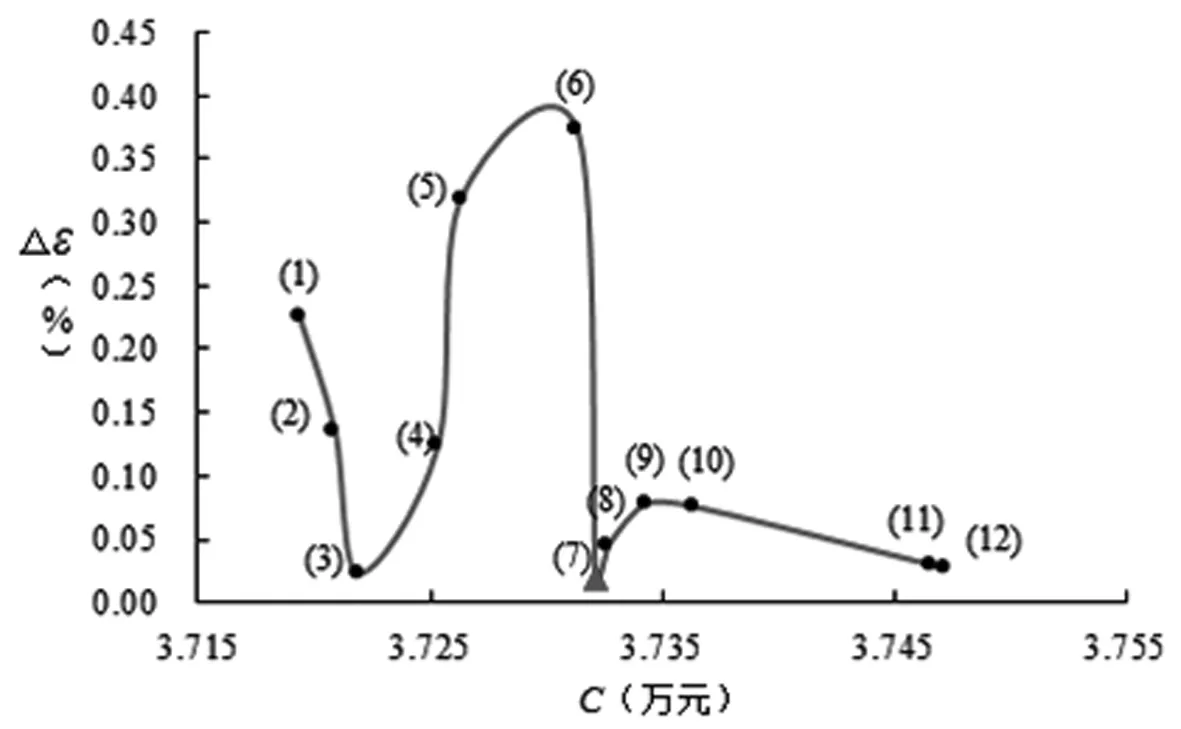
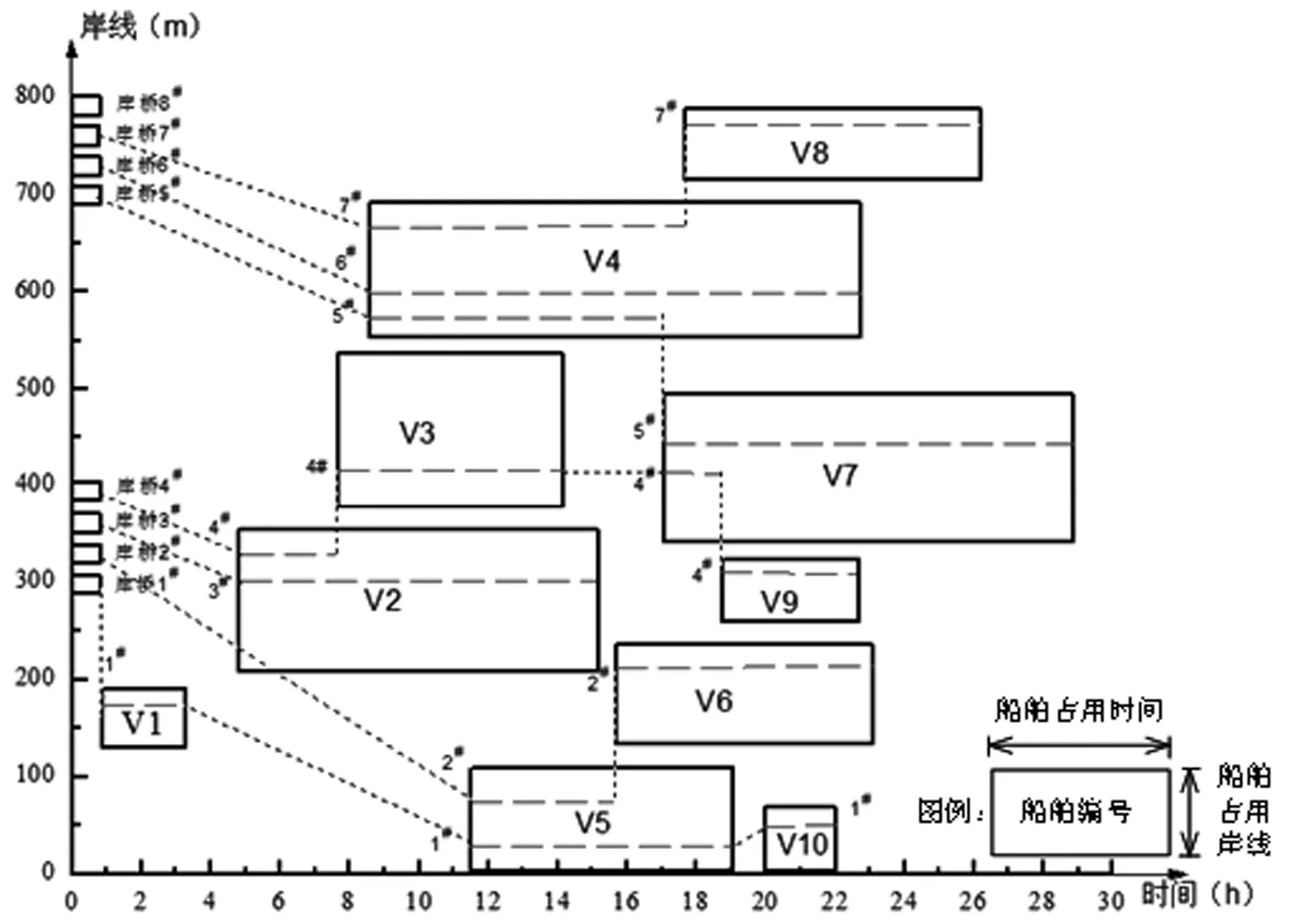
3.2 方案优化
4 结论
