基于统计分析的半潜式平台气隙预报方法研究
2020-10-24卢文月郭孝先魏汉迪
盛 楠,李 欣,卢文月,郭孝先,魏汉迪
(上海交通大学 海洋工程国家重点实验室,上海 200240)
半潜式平台是当今深水生产开发的主要结构形式之一,其适应水深范围广,抵抗恶劣环境能力强,在海洋开发中得到广泛应用。面对复杂恶劣的海洋环境,平台安全性面临严峻的挑战,而气隙是一项十分重要的设计参数[1]。当气隙为负值时,会发生甲板上浪、波浪砰击等现象,极易导致平台结构破坏、设备失效甚至威胁作业人员的安全[2-3]。基于一阶势流理论的数值计算方法[4],因线性简化而严重低估波面升高,与实际差异较大,故不能满足平台安全性要求。 国内外学者针对此问题,分别在理论分析、数值计算、模型试验等方面提出改进方法。
在计算方法及计算思路优化方面,Nielsen[5]针对浮式平台,分别将不同波浪组合下波浪升高的数值计算与模型试验做对比,利用修正简化过程的方法实现气隙计算优化;Eatock等[6]介绍了一个高阶离散元积分方程,提高了一阶和二阶问题的计算效率,同时提高计算精度;特别地,针对二阶波浪力与二阶低频运动问题[7-9],Pessoa与Fonseca基于二阶势流理论,对比5种近似方法计算二阶波浪力,通过二阶传递函数确定运动响应,采用阻尼系数与响应统计值优化预报结果;Vinje则应用概率模型,采用缩小因子更精确表达短峰波下的力与运动关系,提高准确性。
从理论模型角度,除标准线性波浪模型外,Sweetman等[10-12]采用Stokes二阶波浪理论修正水动力传递函数;Borresen等[13]进一步采用5th Stokes波浪理论修正;Kvaleid等[14]则针对平台大幅运动湿表面非线性变化现象,通过增加阻尼项修正线性计算结果。此外,也有一些学者选择不同的统计模型和估计方法分析数据,比如采用高斯分布模型、韦伯分布模型、Gumbel分布以及LH矩法对气隙值进行拟合分布[15-21]。
波浪非线性问题是气隙预报中的重要部分,一般用波浪非线性因子∂反映波浪非线性强度,∂的数值与气隙点具体位置以及浪向角相关。对一座半潜平台在极端波浪下的气隙问题进行模型试验与数值计算,结合统计分析和概率分布拟合方法,计算平台各处在不同海况下的∂值,并与DNV[22]在OTG-13中给出的建议值进行验证和比较。
1 模型试验与数值模型建立
1.1 模型试验
1.1.1 模型系统参数
半潜平台主体结构由甲板,4个方形截面立柱,4个浮体组成。平台关于中心对称,如图1所示,主要参数如表1。试验模型缩尺比为1∶60。
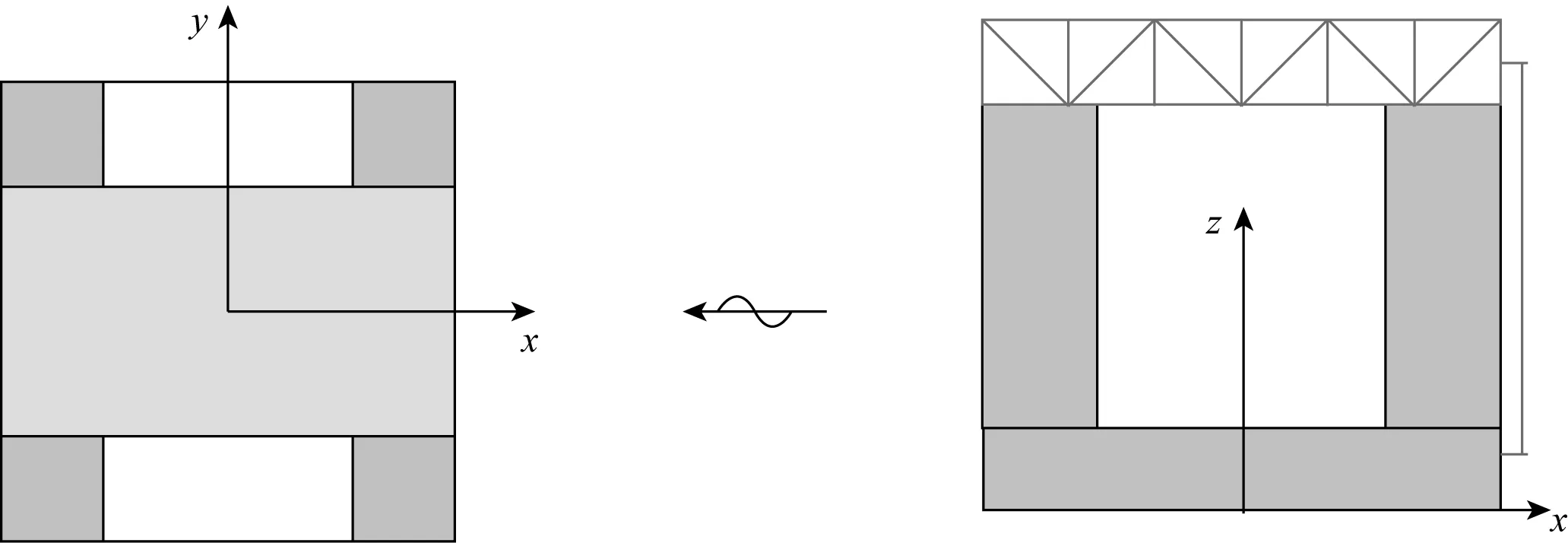
图1 半潜平台结构示意Fig. 1 Semi-submersible platform

表1 半潜平台主尺度Tab. 1 Main scale of semi-submersible platform
模型系泊系统采用等效截断系泊,由4根相同的系泊缆1~4组成,立管系统由2根立管1~2组成,如图2所示。

图2 系泊系统示意Fig. 2 Mooring system
1.1.2 气隙点分布
试验选取平台周围18个点作为气隙点,如图3所示。表2为各点坐标值,测量点静气隙距基线22 m。
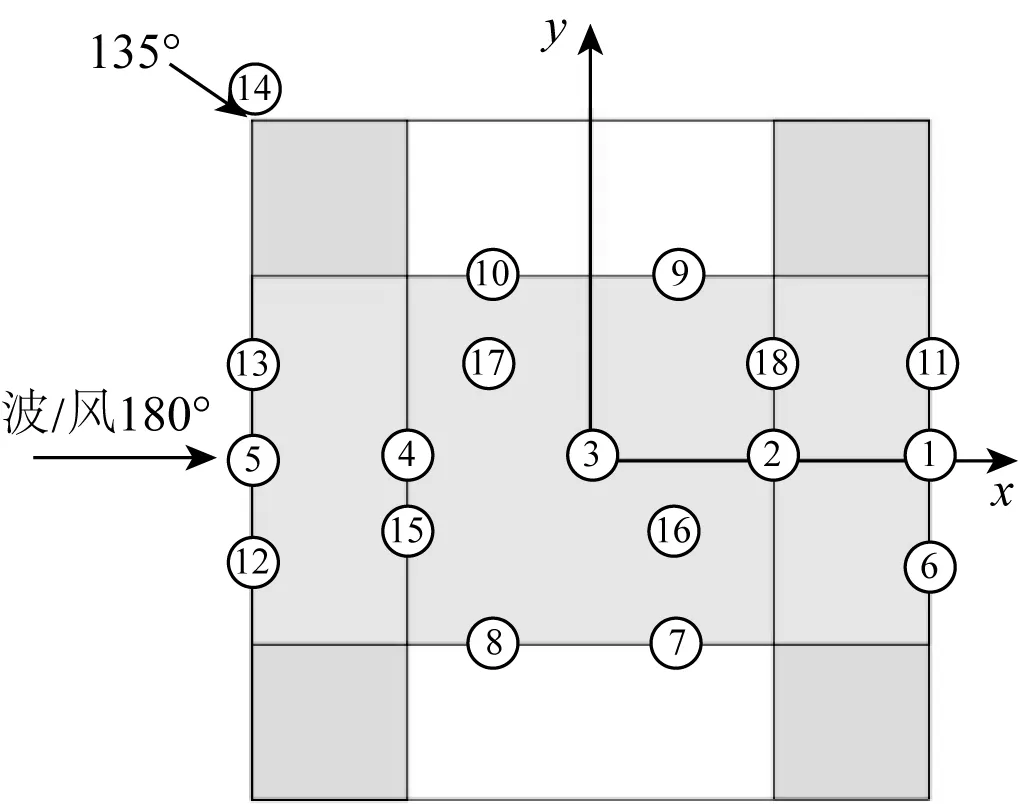
图3 气隙点分布Fig. 3 Point distribution

表2 气隙点坐标Tab. 2 Air gap point coordinates
1.1.3 海洋环境参数
半潜平台实际工作水深为588 m,试验水深为9.8 m。参考南海海域环境,选取7种海况(Jonswap谱)。波浪参数如表3所示,3个浪向角分别为180°、135°、157.5°,同时在水线面上方5 m处加风载荷,平均风载为15 754 kN,与波浪同向。
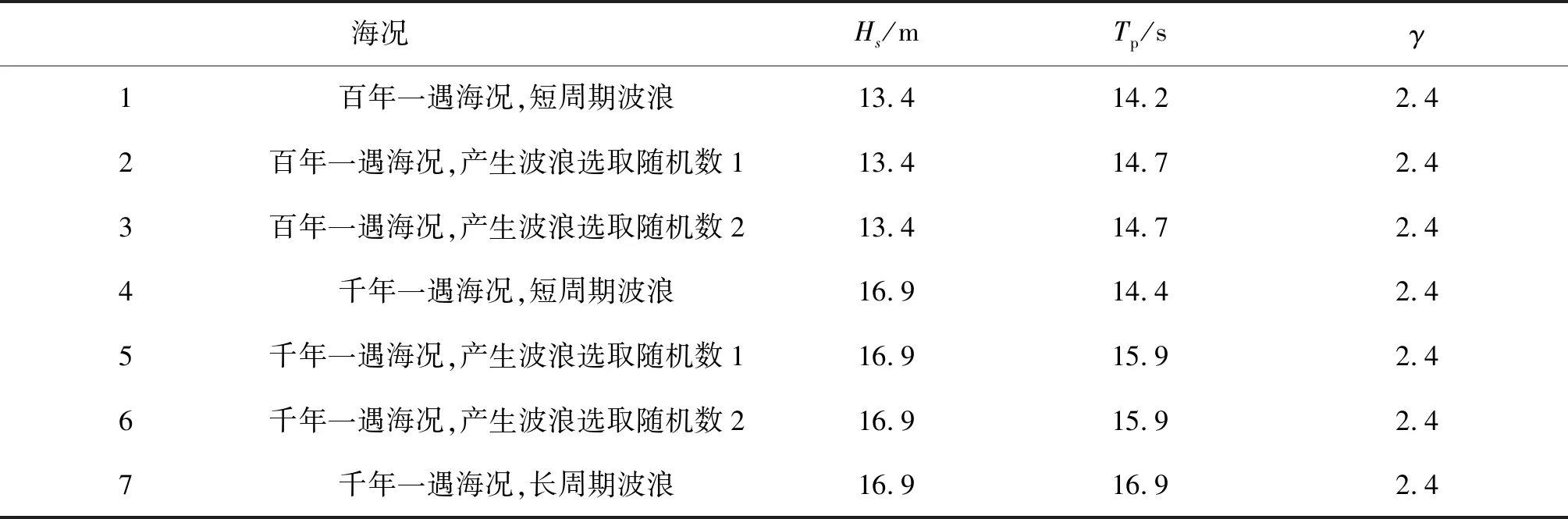
表3 波浪谱参数Tab. 3 Wave spectrum parameters
试验模拟的不规则波时历如图4所示;图5为海况2,海况5试验波谱与目标波谱的对比结果。试验波浪与目标波浪吻合较好,满足波浪环境模拟要求。
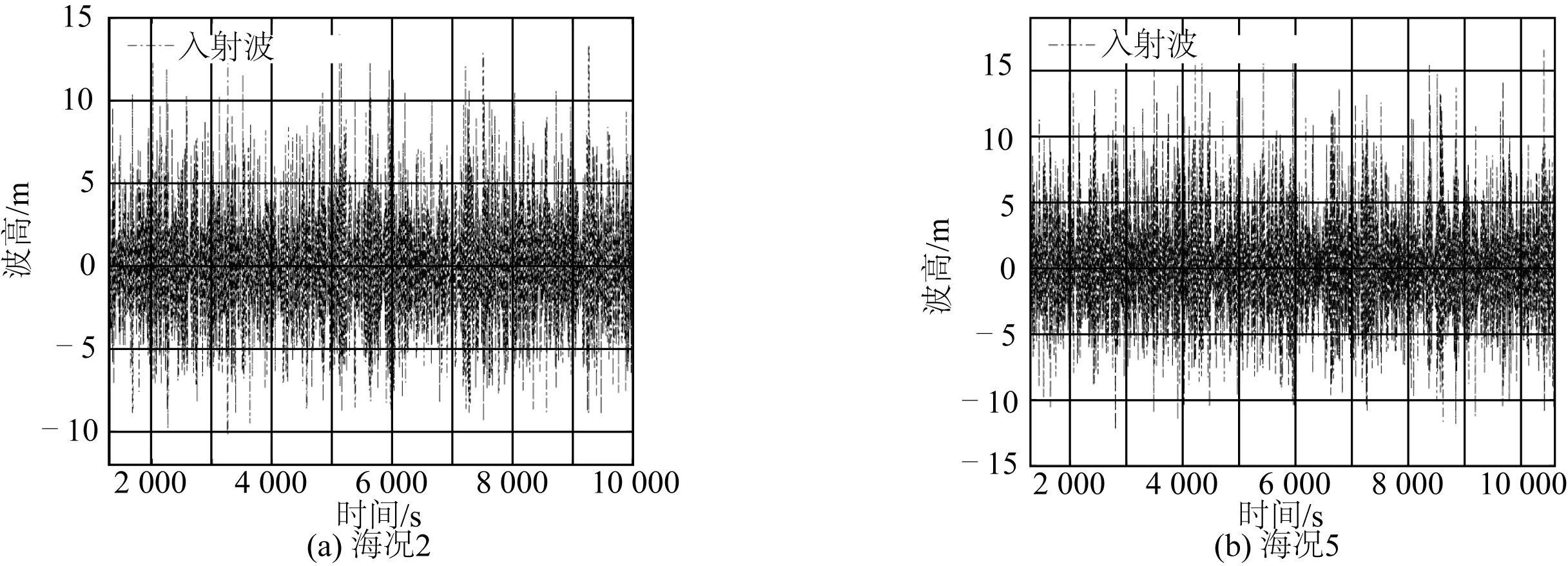
图4 不规则波时历Fig. 4 Irregular wave time history
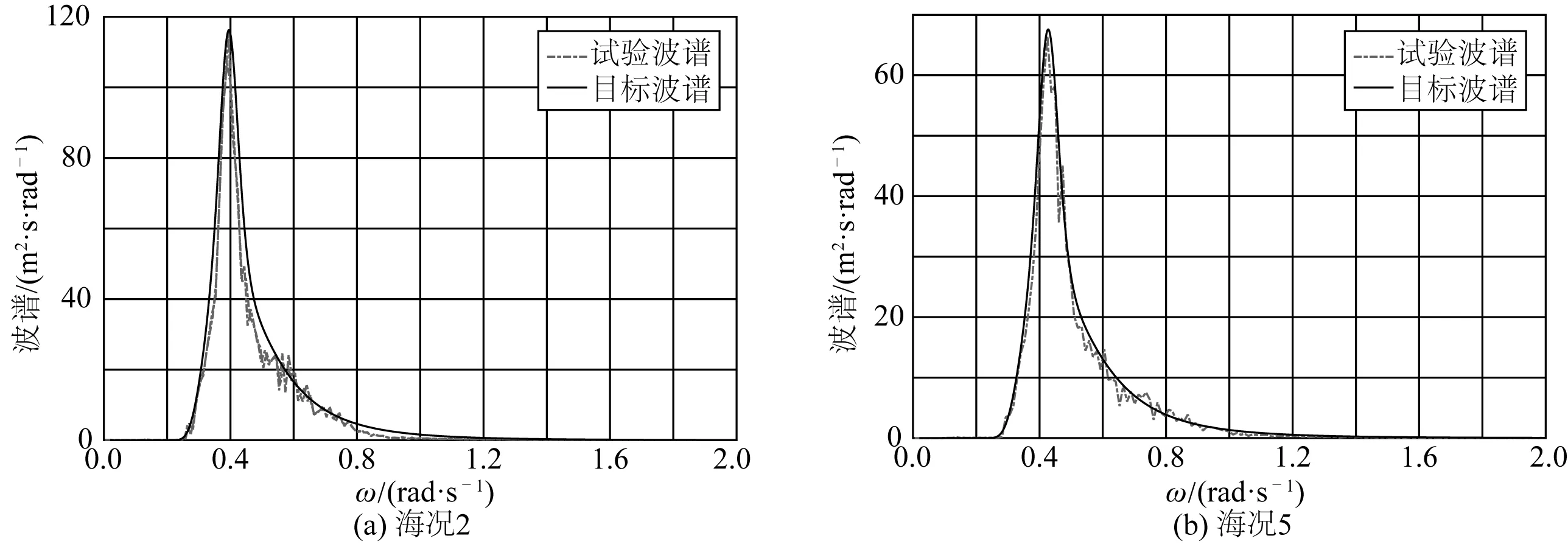
图5 波谱Fig. 5 Wave spectrum
1.2 数值模拟
应用DNV-SESAM/WADAM模块进行频域计算,DeepC模块进行时域耦合计算。建立有限元模型如图6所示,平台及系泊系统如图7所示。

图6 三维模型Fig. 6 Numerical model

图7 系泊系统示意Fig. 7 Numerical mooring system
数值模拟计算首先进行频域计算,得到平台相关的水动力参数,如附加质量,附加阻尼值等,以及频域运动响应函数RAO,波浪载荷响应函数H(ω)等,然后输入试验入射波浪时历数据,基于频域分析及脉冲响应理论,得到平台在对应海况下的运动响应及各气隙点的气隙响应时历,为下文统计分析提供可靠的数据。
1.3 模型试验与数值计算比较
平台自由衰减运动的数值计算与静水试验结果对比如表4所示。由表可知,数值模拟的平台运动周期与模型试验结果对比误差较小,满足水动力计算要求。

表4 静水分析结果对比Tab. 4 Comparison of the natural periods
通过模型试验可确定一点处的相对波面升高以及平台中心垂向位移。因此通过计算求得该点处的垂向位移,结合相对波面升高值,即可确定某一点波面升高的试验结果,进而与数值计算作对比。如图8为2号(180°)海况下波面升高的计算值与试验值,比较可以看出,数值计算结果低估了波面升高极值。

图8 气隙点1在2号海况的波面升高Fig. 8 JON2 Probe1 wave elevation
2 气隙统计分析
2.1 气隙的原理
气隙由三部分组成,静气隙、垂向位移及波面升高,如图9所示。
气隙响应α可表示为:
α(x,y,t)=α0(x,y)-χ(x,y,t)
(1)
χ(x,y,t)=(x,y,t)-zp(x,y,t)
(2)
zp(t)=ξ3(t)+ysin[ξ4(t)]-xsin[ξ5(t)]
(3)
其中,α0为静气隙,χ为相对波面升高,η(t)为响应波高,zp(t)为平台垂向位移;ξ3(t),ξ4(t),ξ5(t)分别为平台垂荡、横摇和纵摇运动。
其中响应波高由三部分组成,即入射波、绕射波、辐射波。
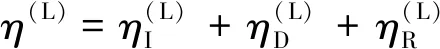
(4)
结合波浪谱,一阶响应谱为:

(5)
Hr(ω,α)=Hη(ω,α)-Hδ(ω,α)
(6)
式中:Hη,Hδ分别为波面升高传递函数和垂向位移传递函数。
若考虑非线性运动,则:
zp(x,y,t)=zmean(x,y)+zWF(x,y,t)+zLF(x,y,t)
(7)
其中,zmean(x,y)为浮体初始倾斜产生的垂向位移,zWF(x,y,t)、zLF(x,y,t)分别为波频运动响应和低频运动响应。
η=ηI+ηD+ηR
(8)

(9)
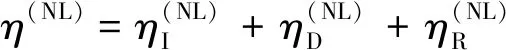
(10)
η(x,y,t)=ηWF(x,y,t)
(11)
ηWF(x,y,t)=η(L)+η(NL)≈∂η(L)
(12)
式中:上标(L)为线性,(NL)为非线性;ηWF为波频响应波高;∂为波浪非线性因子。

图9 气隙示意Fig. 9 Air gap variable definitions
2.2 统计分析方法
假设波面升高服从双参数Gumbel 分布,概率密度函数为:
fG(x,a,b)=-aexp[a(x-b)]exp{-exp[a(x-b)]}
(13)
累计分布函数为:
FG(x,a,b)=exp{-exp[a(x-b)]}
(14)
将计算值与试验值分别进行分布拟合,进而求得各气隙点在各海况下的非线性因子∂值,具体分析方法如下。
首先进行Gumbel 分布拟合,累计概率分布函数为:
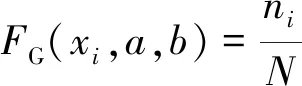
(15)
其中,N为相对波浪升高峰值个数(3 h海况),ni为数据中波浪峰值不超过xi的个数。
取对数,设:
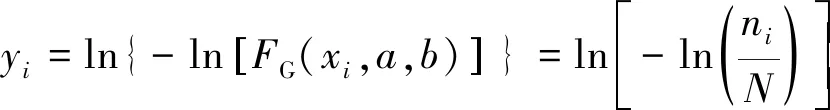
(16)
其中,a、b通过最小二乘法确定,即满足:
min[yi-a(xi-b)]2
(17)
取90% Gumbel分布值:
η90=ln[-ln(1-1/0.9N)]/a+b
(18)
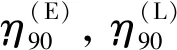
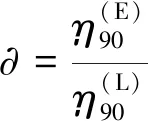
(19)
图10,图11分别为气隙点1,3,5,6,13,15在2号(180°),5号(180°)海况下的拟合结果。

图10 2号(180°)海况模型试验波面升高拟合Fig. 10 Test wave elevation ditribution, JON2, 180°
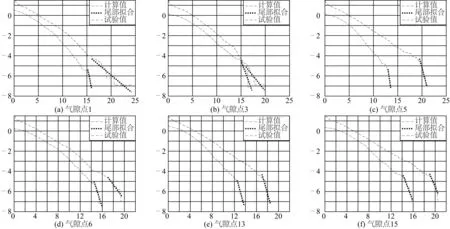
图11 5号(180°)海况模型试验波面升高拟合Fig. 11 Test wave elevation ditribution, JON5, 180°
2.3 波浪非线性因子 ∂计算结果
平台18个气隙点在每个海况下的波浪升高数据,通过Gumbel 分布拟合后,求得对应的波浪非线性因子∂值。表5为气隙点处波浪非线性因子∂均值结果。

表5 ∂计算结果Tab. 5 ∂ calculated value
图12为不同海况下各点∂值与均值结果比较。图13为浪向角180°,2号海况下,根据各点横坐标表达的∂均值分布。
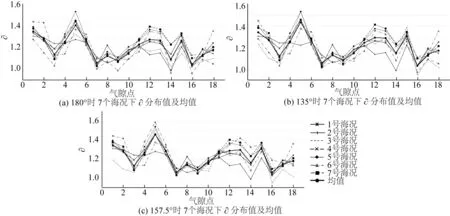
图12 7个海况下∂分布值及均值Fig. 12 ∂ distribution in 7 wave conditions and mean value
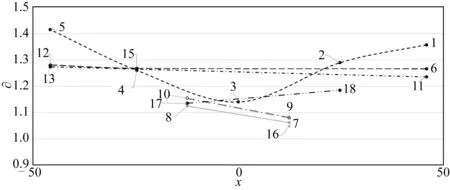
图13 2号(180°)海况下不同横坐标气隙点∂平均值Fig. 13 ∂ mean values at 18 positions, JON2 wave, 180°
2.4 结果分析
根据OTG-13中0°, 45°浪向角下半潜平台∂分布图(图14),可知平台在180°和135° 浪向角下各气隙点的经验值,如表6所示。
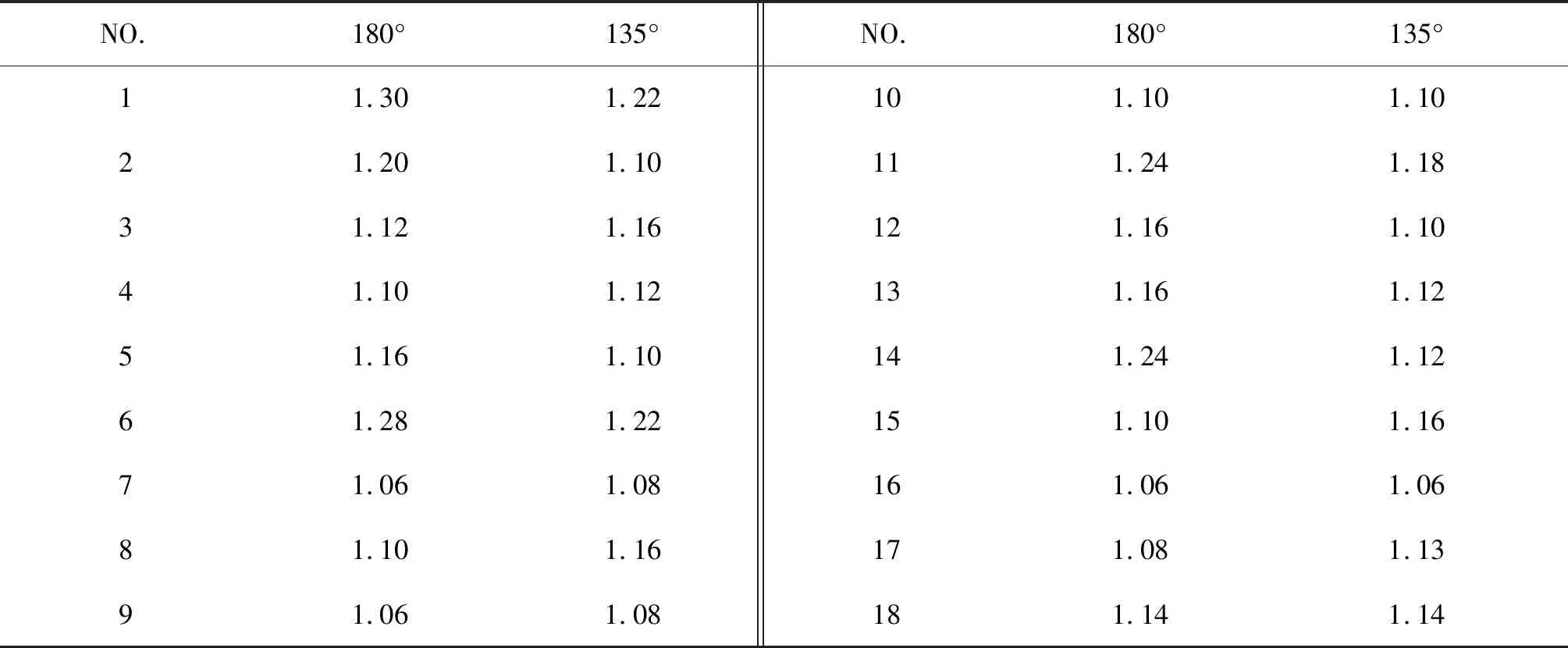
表6 OTG-13气隙点∂值Tab. 6 OTG-13 recommended values
∂ 经验值与计算值比较结果如图15所示。

图14 ∂取值分布图Fig. 14 ∂ distribution
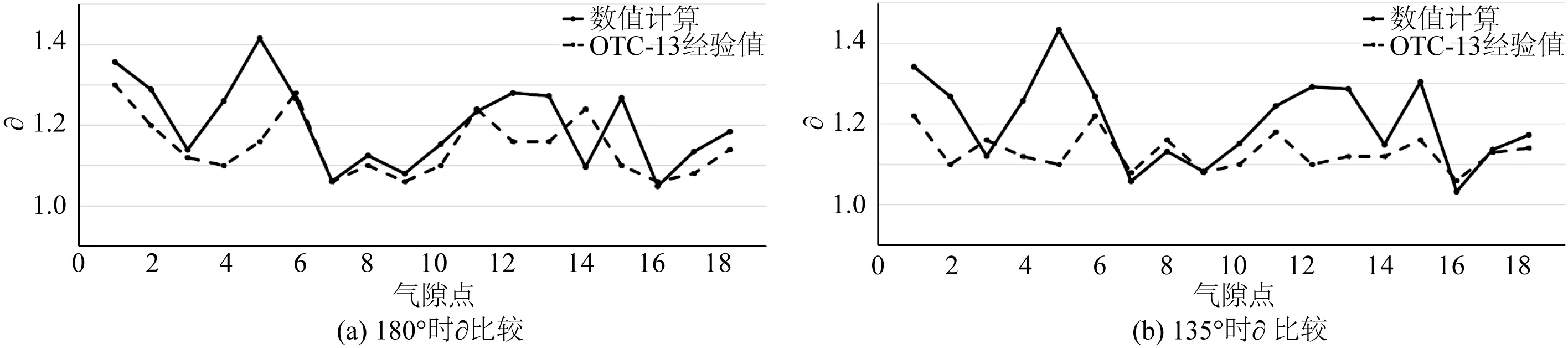
图15 ∂经验值与计算值对比Fig. 15 ∂ comparison between recommended values and calculated values
由以上结果分析:
1) 模型试验与数值模拟比较
数值计算的波面升高幅值较模型试验小(图8),证明基于线性势流理论的数值模拟低估了波面升高现象,不能保证气隙预测的准确性以及平台安全性,同时考虑波浪非线性效应对于气隙问题是非常重要的。
2) 波浪非线性因子∂计算结果分析
① 相同浪向角,不同波浪海况下,各气隙点∂值变化趋势基本一致,即各位置处波浪非线性效应的相对大小关系一致(图12);
② 根据∂计算值分析,位于平台下浮体顺浪面外侧中点(5号)处∂值最大,其次点1、6、11、12、13处∂值皆较大且接近(图13),即下浮体外侧介于两立柱之间处波浪非线性效应最为显著,而下浮体空间内的点,由于距离平台结构较远,波面升高非线性效应较小;∂ 极大值点(如点5)在千年一遇海况下较百年一遇海况大,极小值点(如点16)在对应海况下较小,即波浪非线性效应强的位置在恶劣海况下,非线性效应被放大,相应地非线性效应弱的位置,结果相反。
3) 与OTG-13经验值比较
① 浪向角180°,点3、6~11、16~18的∂计算值与经验值比较一致,点2、4、5、12~15号点差异较大(图15(a));135°浪向角时,点3、6~10、14、16~18号的∂计算值与经验值比较一致,点1、2、5、12、13、15差别较大(图15(b))。157.5°浪向角情况与180°一致。
② 位于平台下浮体附近顺浪侧位置(点5、12、13)波浪非线性最强,且平台下浮体附近的∂值皆与建议值差异较大,而下浮体空间内距离平台结构较远的点,计算结果与建议值一致,可参考建议值。特别地,位于立柱斜后方的14号气隙点,在180°浪向下,∂ 计算值小于建议值,在135°浪向角下 ∂计算值大于建议值,即立柱附近位置的波浪非线性强度受浪向角影响显著。
3 结 语
主要针对极端海况下半潜平台气隙响应特性及预报分析方法进行研究。结合模型试验与数值计算,采用Gumbel分布拟合,计算波面升高非线性因子∂值,并与OTG-13经验值进行比较。得到如下结论:
1) 在数值计算中,只考虑线性波浪忽略高阶成分,会导致波面升高幅值结果偏小,低估平台气隙响应,无法满足。
2) 经过Gumbel概率拟合分布后计算得到的波浪非线性因子∂计算结果与OTG-13的建议值并不完全一致。在靠近平台下浮体附近位置的气隙点,其计算值明显大于建议值,即统计分析得到的波浪非线性强度高于经验值,要重点考虑。而距离结构较远的位置,其计算值与经验值较为一致,非线性因子∂值可参考经验值。此外,位于立柱附近的气隙响应受浪向角影响较大(点14),需要重点关注。
3) 在∂值较大的位置,当波浪环境越恶劣时,对应的∂值越大,波浪升高非线性效应越强;在∂值较小的位置,当波浪环境越恶劣,相应的值越小。
