基于图像处理的异重流与系泊结构物作用模型试验研究

陈欣桐，李 欣，胡智焕，吴 骁

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240; 2. 高新船舶与深海开发装备协同创新中心，上海 200240)

异重流，也称重力流、密度流，是两种密度相近的流体，因密度差异而发生的相对运动，高密度流体潜入低密度流体下方的现象[1]。异重流运动过程能量损失小且不同流体的掺混相对较少[2]，导致其在形成发展过程中，速度能量不断增大，产生巨大的破坏能力。在我国长江入海口、珠江入海口等海域，异重流广泛存在。异重流所携带的巨大能量给海洋工程的安装与作业带来不小的考验，影响工程的安全与质量[3-4]。由于异重流往往具有较大的冲击速度，加之海洋工程结构形式多样、体量庞大，对海洋异重流的存在对海洋工程结构设计、施工及全寿命运营、维护过程的影响必须予以重视。

异重流现象在自然界许多场合以及实际工程中存在。许多工程领域，在致力于解决工程与环境问题时，需要有关异重流知识的逐步积累。在气象学研究中，海风前锋、山地冷空气以及沙尘暴的研究属于空气异重流范畴。在地质学研究中，大陆坡上海底峡谷的形成以及雪崩现象也与异重流的形成有关。在水利工程研究中，水库泥沙的淤积与排沙正是利用的异重流相关特性以减少水库泥沙的淤积。在环境工程中，有害重气体的泄露、海上油船失事等过程均形成异重流造成环境污染[5]。

Von Karman[6]率先讨论了大深度下恒定异重流头部运动的理想模型，提出Von Karman模型，得出异重流头部流速理论计算公式。Benjamin[7]采用Bernoulli方程以及静水方程，得出了在无黏理想水流条件下，异重流的初始厚度是其流动后厚度的两倍的结论，同时他提出异重流的流动历程十分稳定，能量耗散少。Simpson等[8-9]进行异重流头部试验，分析研究异重流头部运动和形状，在底部无阻力和有阻力时头部与周围水体混合的情况，并同无黏液体理论所分析的无阻力无混合的异重流头部运动进行比较，并将水流头部分为三个区域：未被混合的重液体、未被混合的轻液体和混合层。随着测量技术的发展，试验测量手段越来越多，越来越精确，对于异重流的性质例如浓度场、速度场、涡量场的研究越来越深入。Marleau等[10]对溃坝式异重流在斜坡上的演化机理进行了试验研究，并采用粒子图像测速(PIV)技术测量流场的变化。随着异重流理论的发展和试验数据的大量积累和消化，以及计算机技术的发展，用数值计算的方法模拟异重流的能力也有了很大的提升，不少学者采用数值计算的方法对异重流进行了研究。Gonzalez-Juez等[11]采用大涡模拟的方法，研究了异重流与固定式结构物的相互作用，研究结构物的受力以及流场特性。Gonzalez-Juez和Meiburg[12]应用浅水理论，研究了异重流与固定式结构物相互作用后，异重流的头部高度和流速。Tokyay等[13]采用大涡模拟的方法研究固定于海底的周期性排列结构物受异重流的作用，并研究不同结构物尺度的影响。

开闸式异重流试验是开展异重流相关研究十分简单且有效的方法，因此对于异重流的研究多采用开闸式的方法，同时采用模型试验的方法也非常的直观，现已进行了多种试验条件下的试验。然而，很少有学者讨论和研究开闸式异重流对系泊结构物的作用。研究受异重流影响系泊结构物的运动特性具有较高的工程应用价值，例如港珠澳大桥沉管安装、海底线缆的布置等。然而目前对于异重流与系泊结构物之间的相互作用研究较少。因此，研究系泊结构物在异重流作用下的运动响应具有重要研究价值，对于受异重流作用的海洋结构物的安装与作业具有一定指导作用。

运用模型试验的方法，研究系泊结构物与开闸式异重流相互作用，分析其运动特性，对比不同密度异重流作用下结构物运动特性的变化，以及同一密度比的异重流对处于不同深度结构物运动的影响，利用高速摄像机拍摄结构物的运动，通过图像处理算法处理试验数据，分析结构物的运动特性。

1 开闸式异重流模型试验

1.1 试验布置

模型试验布置如图1所示。试验在一个由有机玻璃板拼接而成的矩形水槽里进行。一块有机玻璃板将盐水和淡水分隔开。4根有机玻璃条用于固定挡板，保障挡板的顺利抽插。挡板两侧因密度差异会产生压强差，在挡板上放置铁块，防止倾斜。凡士林涂抹在挡板边缘用于密封。起初，挡板两侧为高度相同的盐水和淡水。结构物的形式为一方形柱体，4根线性弹簧用于模拟结构物系泊方式。

采用2台高速摄像机拍摄，计算机同时控制这2部摄像机的开机和停止。1号高速摄像机用于拍摄结构物以获得其运动特性，2号高速摄像机拍摄异重流流动过程。摄像机距离水槽前壁1.5 m。直流光源用于提供连续稳定光源，保证所有照片不会出现黑暗的情况。摄像机镜头误差来源于镜头带来图像畸变，采用高素质镜头，同时使结构物尽量置于镜头中心，因为越靠近镜头中心变形越小，降低镜头带来的误差。

图1 异重流试验布置Fig. 1 Arrangement of gravity current experiment

1.2 试验基本参数

模型试验布置示意如图2所示。表1为具体参数。

图2 模型试验布置Fig. 2 Model test layout

表1 模型参数Tab. 1 Model parameters

为了讨论异重流密度比和结构物位置的影响，设置如下条件：1)盐水密度ρ2为1 040、1 030、1 020 kg/m3；2)淡水密度ρ1为997 kg/m3；3)结构物深度d/D为0.120、0.275、0475。试验共有5个工况，如表2所示，每个工况重复3次，重复工况使用R1、R2、R3表示。

表2 异重流试验工况Tab. 2 Conditions of lock-exchange experiment

异重流产生的根本原因是水槽内盐水与淡水之间的密度差，初始有效重力加速度g*表示为：

(1)

物理量时间t*、x方向位移x*、y方向位移y*采用如下的无因次形式表达：

(2)

(3)

(4)

其中，V为异重流释放后头部速度。

2 试验模型验证

2.1 异重流演化形态

图3为密度比ρ2/ρ1=1.04时异重流的流动过程。可以发现，开闸式异重流匀速前进，其初始高度是其锋头高度的两倍，并且在异重流演化的过程中在液体交界面处产生明显的翻卷和混合，这种现象称为Kelvin-Helmholtz不稳定现象，这是由于两种液体之间存在剪切速度差，两种液体从层流变为湍流。这说明试验中异重流的演化特点符合Benjamin经典理论[7]所描述的特征。密度比为ρ2/ρ1=1.03与ρ2/ρ1=1.02时异重流的演化过程也具有相同特征。

图3 密度比ρ2/ρ1=1.04异重流演化过程Fig. 3 The evolution process of gravity current when ρ2/ρ1=1.04

2.2 异重流头部速度

基于能量守恒，Benjamin[7]推导出异重流头部速度公式。

(5)

Shin等[14]引入浅水理论，考虑到长周期的内波会耗散部分能量。

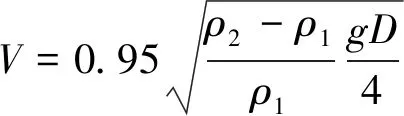
(6)

如图4所示，将异重流头部速度的模型试验值和理论计算值进行比对。对比发现，理论计算结果稍高于模型试验结果，这是由于模型试验存在湍流混合作用带来的能量损失。

图4 头部速度试验值和理论值对比(ρ2/ρ1=1.04)Fig. 4 Comparison of experimental and theoretical values of front velocity (ρ2/ρ1=1.04)

2.3 数值计算结果对比

试验模型的验证对比了数值计算的结果。数值计算采用STAR-CCM+软件，湍流模拟采用大涡模拟，运动网格采用重叠网格方法，对比工况3-1的模型试验结果与该工况参数完全相同的数值计算结果，对比其在x、y轴方向的运动以及绕着z轴转动这3个自由度的运动，对比结果如图5、图6和图7所示。

图5 x方向运动对比结果Fig. 5 x-direction motion comparison results

图6 y方向运动对比结果Fig. 6 y-direction motion comparison results

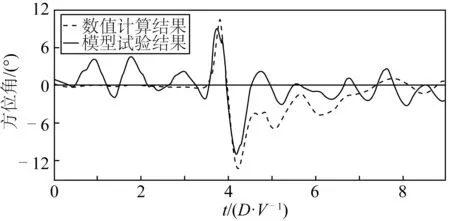
图7 绕z轴转动对比结果Fig. 7 Comparison results by rotating around the z axis

图5为结构物在x轴方向运动的模型试验与数值计算结果对比。在初始阶段，异重流运动早期未与结构物发生作用，数值计算结果x方向的运动值为0，而模型试验结果由于受到自由液面的影响一直在0值附近波动。之后异重流与结构物发生作用，结构物的运动产生了一次极小值和一次极大值，对比发现极值产生的时间和大小，模型试验与数值计算结果几乎完全相同。之后数值计算结果与模型试验结果在运动趋势上具有一致性，在具体数值上略有差异。结构物在y轴方向的运动和绕着z轴的转动也有相同的特征。

通过对比发现，x、y轴方向的运动以及绕着z轴转动这3个自由度的运动，数值计算结果与模型试验结果在极值以及极值的产生时机保持一致。之后的运动，数值计算结果与模型试验结果在运动趋势上具有一致性，在具体数值上略有差异。以上对比可以说明，模型试验结果和数值计算结果可以相互印证。

3 图像处理算法

图像处理流程如图8所示，通过图像处理算法分析高速摄像机所拍摄的图片，从而得到试验所需的结构物的运动数据。

图8 图像处理流程Fig. 8 Image processing flow

图像处理流程方法如下，利用RGB值识别结构物的位置，得到结构物的中心位置。结构物的四角坐标的估测值利用中心位置坐标以及估测旋转角可以计算得到，如图9所示。

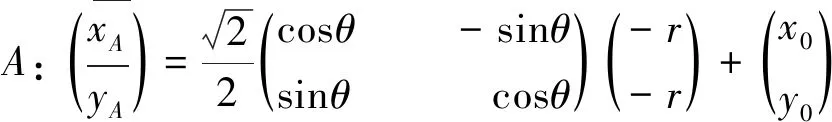
(7)

(8)

(9)

(10)

结构物四角实际坐标如下：

(11)

计算结构物四角的实际坐标与估测坐标的方差，其导数为零：

(12)

求解上式，可得：

(13)

图9 方柱运动捕捉算法Fig. 9 Square column motion capture algorithm

4 试验结果分析

4.1 异重流密度影响

通过图像处理算法，得出结构物3自由度的运动时历图。图10，图11和图12为位于同一深度(d/D=0.475)的方柱在不同密度比(ρ2/ρ1=1.04,ρ2/ρ1=1.03,ρ2/ρ1=1.02)的异重流作用下的3自由度运动响应。

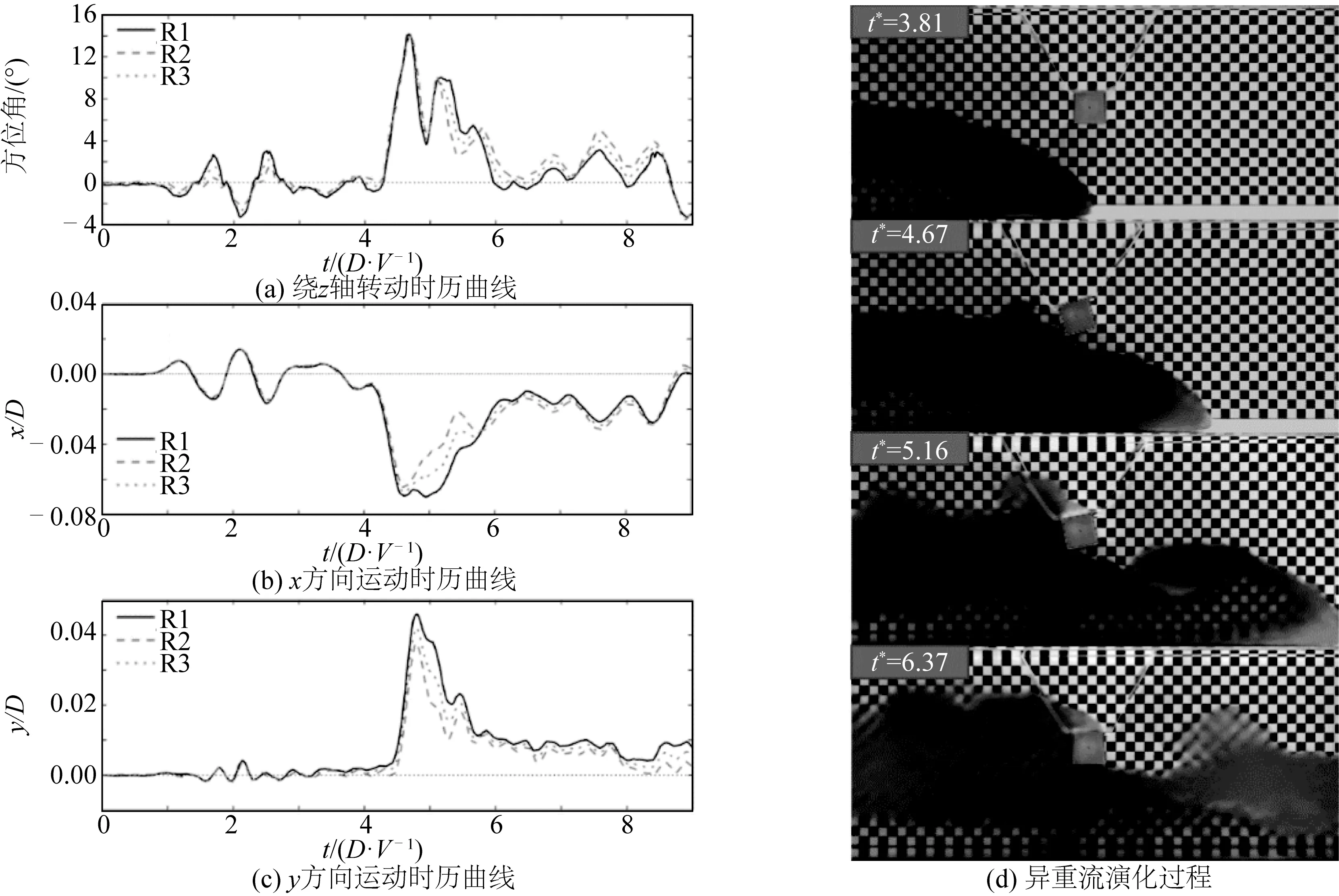
图10 方柱运动响应(工况3-1)Fig. 10 Motion response of cylinder (Exp.3-1)

以图10工况3-1密度比为ρ2/ρ1=1.04的异重流为例分析，可以看出，异重流作用下的方柱运动幅度很大，在初始阶段，异重流运动早期未与结构物发生作用，3个方向结构物的运动值均在零值附近波动，当异重流的头部逐渐靠近结构物，结构物周围的密度逐渐增高，在正y方向上产生极大值。当异重流头部接触到结构物后，对结构物产生瞬时的冲击，头部分成两部分，第一部分沿着结构物与槽底之间的空隙流动，第二部分越过结构物的上方之后又在重力的作用下回到底部，此时在3个方向上均产生了极大值。之后，流场逐渐进入稳态时，结构物在异重流的作用下保持了正x、y方向一定的偏移和一定的方位角。

工况3-2密度比为ρ2/ρ1=1.04的异重流与ρ2/ρ1=1.03的异重流作用下的方柱具有相同的运动趋势，区别在于高密度比异重流作用下的方柱运动更加剧烈。

对于工况3-3密度比为ρ2/ρ1=1.02异重流，方柱的运动相较于工况3-1具有一定的差异，此时方柱的运动幅度很小，其在x方向的运动以及绕着z轴的转动均在零值附近波动，没有出现明显的极值，通过对比，能够得出异重流的密度比越大，异重流头部速度越大，方形柱体的运动越剧烈的结论。

4.2 方柱位置的影响

图10，图13和图14为不同深度的方柱在同一密度比(ρ2/ρ1=1.04)的异重流作用下的3自由度运动响应。为了研究结构物的深度对其运动的影响，对比各个工况下结构物3自由度运动时历曲线，如图15所示。

对于x轴方向的运动，工况1-1中结构物处于高密度流体非混合层，高密度流体沿x轴正向运动，因此结构物在流体力的作用下向x轴正向移动且在一段时间内保持在x轴正向的范围。工况2-1中结构物处于混合层，在该范围内有盐水和淡水剧烈掺混，同时产生湍流，因此结构物不是只朝某一方向运动，而是沿x轴正负方向摆动，此时流场紊乱造成结构物的运动也更加复杂。工况3-1中结构物的位置较高，受到淡水的主导作用，向负x方向运动。

对于y轴方向的运动，结构物周围的密度改变使得其所受浮力改变引起其在y轴方向的运动，工况1-1和工况2-1均出现了明显的负y方向运动，此时高密度流体正越过结构物的上表面，在重力的作用下回到槽底。在流场进入稳态后，工况1-1的结构物周围流场密度最高，其在正y方向上的偏移也就越大。

对于绕着z轴的转动，其运动规律与x轴方向的运动较为相似，工况1-1中结构物处于高密度流体非混合层，结构物在流体的作用下产生顺时针的转动。工况2-1中结构物处于混合层，在该范围内有盐水和淡水剧烈的掺混，此时结构物会产生正负两个方向的旋转。工况3-1中结构物的位置较高，受到淡水的主导作用，产生逆时针转动。

图15 方柱处于不同深度时对运动响应影响对比(ρ2/ρ1=1.04)Fig. 15 Comparisons of motion responses of cylinder at different depths (ρ2/ρ1=1.04)

5 结 语

应用开闸式异重流模型试验的方法，对系泊结构物在异重流作用下的运动响应进行了研究。利用图像处理技术处理由高速摄像机拍摄的结构物运动图片，从而获得结构物运动的时历曲线。对比讨论了不同密度比的异重流对处于相同深度方柱运动的影响以及同一密度比的异重流对处于不同深度方柱运动的影响。

研究结果表明，利用图形处理算法能够较好地处理异重流模型试验中结构物运动的问题，模型试验结果与数值计算结果契合良好。结构物运动受异重流密度的影响较大，结构物的运动幅值随着密度的增大而增大。方柱的运动特性也与其所处的深度有关，其与异重流混合层和非混合层的相对位置是影响其运动的主要因素。处于高密度流体非混合层的结构物受到异重流的作用会产生大幅度的顺时针旋转和正x方向偏移；位置较高的结构物受到淡水的主导作用，会产生逆时针旋转和负x方向偏移。位于盐水与淡水剧烈混合区域的结构物并不会产生单一方向的偏移，而是在平衡位置附近波动。结构物的位置越深，其周围流体的密度更大，其在正y方向上的偏移也就越大。