基于矩阵分析法的回转清理筛运动参数仿真优化*

伍 毅

（广州商学院 信息技术与工程学院，广州 510320）

回转清理筛是由多层做回转运动的筛面所组成，物料在筛选过程中，筛面运动使物料颗粒间产生相互碰撞，物料颗粒与筛面间产生摩擦，各种运动较为复杂。为探求筛体运动参数对筛分性能的影响，作者先借助离散元仿真软件Solidworks 建立回转清理筛三维实体模型，然后通过多因素、多指标正交试验设计并运用EDEM 软件对筛选过程中筛面上物料流运动情况进行数值仿真模拟，并利用矩阵分析的方法进行优化，借此为回转清理筛运动参数优化设计提供一些理论依据。本文着重介绍基于矩阵分析法的回转清理筛运动参数仿真优化。

1 仿真试验方案设计

1.1 仿真参数的选择

筛分效率是衡量清理筛的重要指标，而影响回转清理筛筛分效率的因素很多，如筛面长度、宽度、筛面倾角、筛体回转直径、回转频率和谷物颗粒及杂质含量等，都会影响回转清理筛的筛分效率和工作效果。因此，正确选择回转清理筛的运行参数是其优化设计中十分重要的内容，故从提高筛分效率角度选择筛面回转半径、筛面倾角、回转频率及含杂率等4 个主要参数作为控制变量进行模拟和优化。

1.2 评价指标的确定

筛分效率是衡量回转清理筛工作效果的重要指标。它是指筛分时实际得到的筛下物料的重量与入筛物料内所含可过筛物料的重量之比,反映了筛选工作效果。另一方面，物料在筛面上的平均推进速度决定了筛选的工作效率，推进速度快，物料处理量就大，回转清理筛的产量就高。在筛选过程中，我们既追求好的工作效果，又希望得到高的工作效率。因此，选择筛分效率和物料推进速度作为衡量并获取最佳的筛选运动参数的两个评价指标。

1.3 多因素、多指标正交试验设计

采用正交试验设计方法，选择筛面回转半径A、筛面倾斜角度B、筛面回转频率C 及含杂率D 等4因素3 水平，进行多因素、多指标仿真实验，其因素和水平及仿真模拟试验数据如表1、表2 所示。

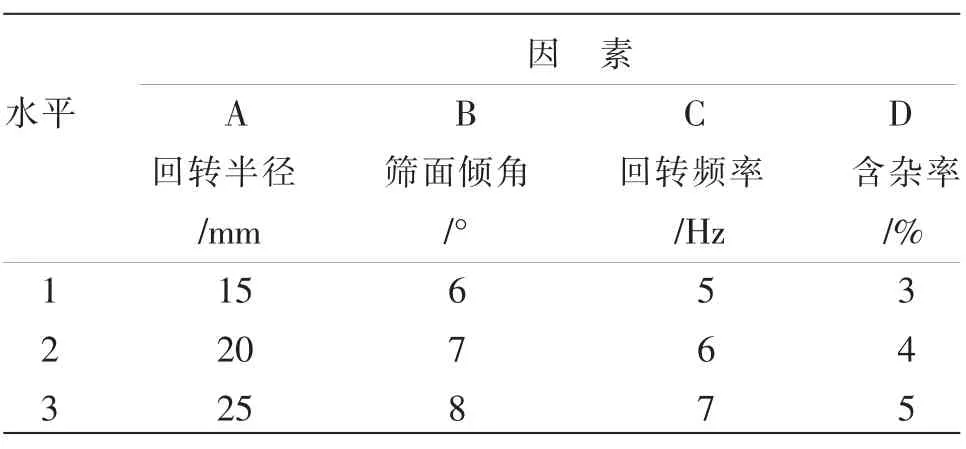
表1 因素水平设计

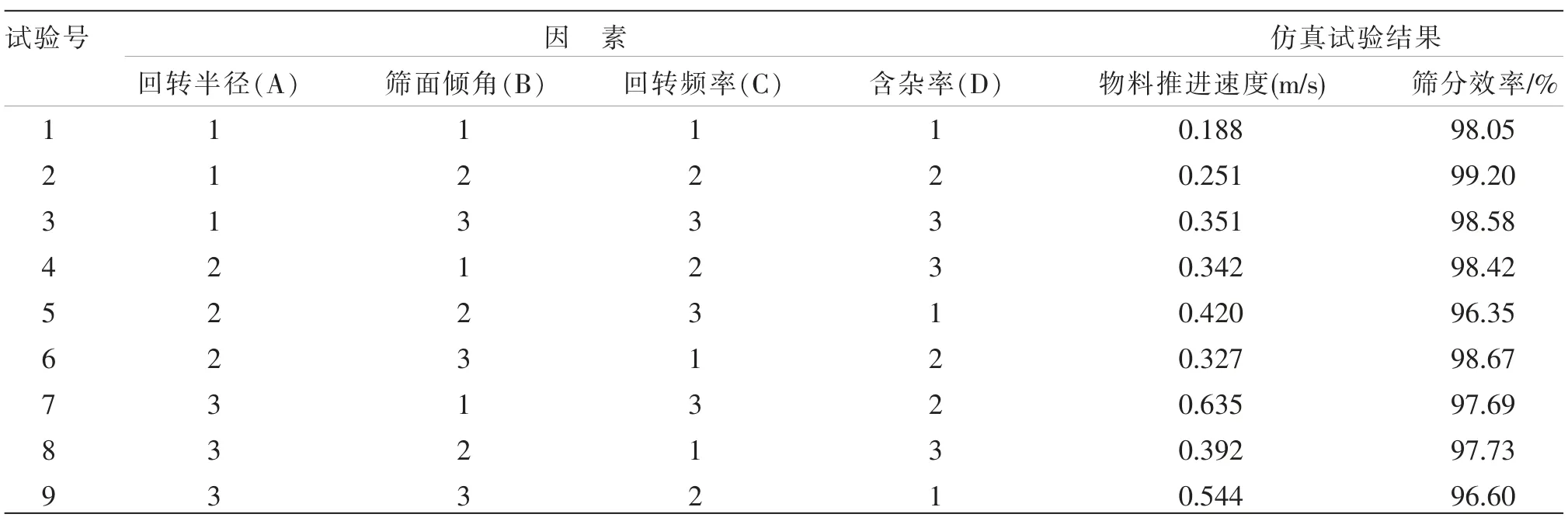
表2 正交试验设计仿真数值模拟结果

1.4 仿真结果的极差分析

根据正交试验分析的方法得到极差分析结果如表3 所示。

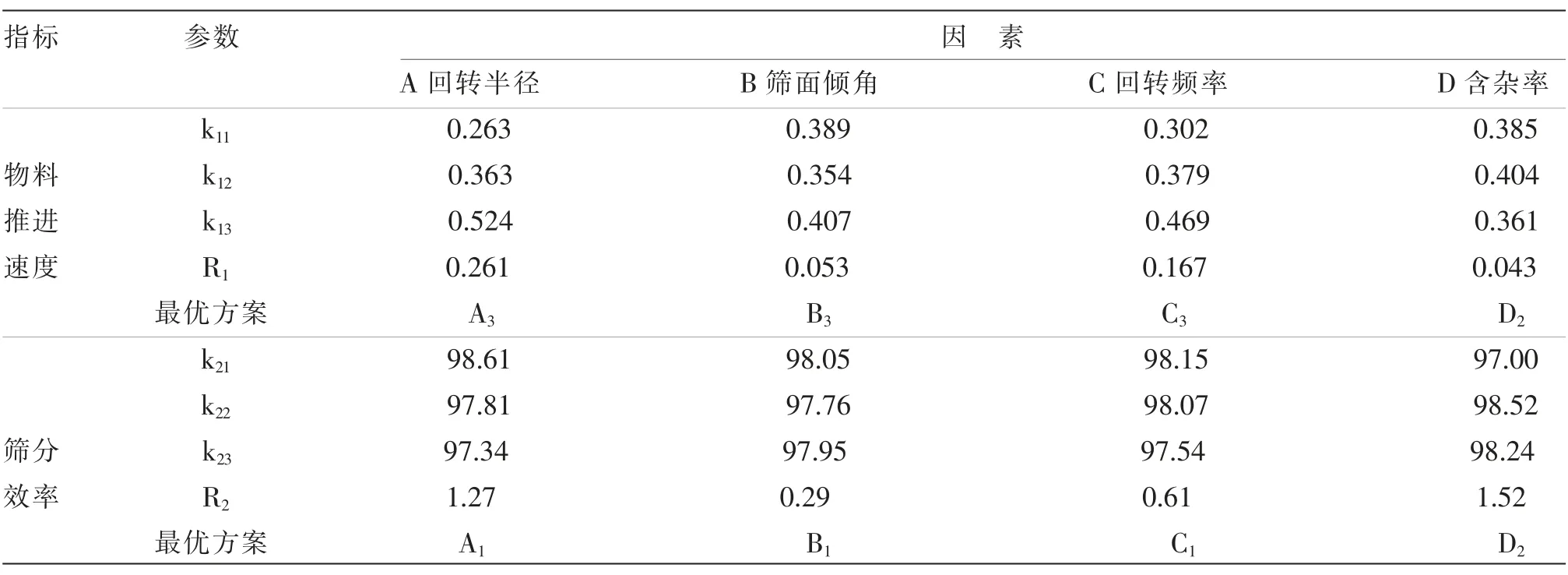
表3 仿真数值模拟结果极差分析

由极差分析可知，从单指标评价的角度来看，影响物料推进速度快慢的因素主次顺序为：因素A(回转半径)＞因素C(回转频率)＞因素B(筛面倾角)＞因素D(含杂率)，并且随着回转半径、回转频率、筛面倾角的增大，物料推进速度呈增大的变化趋势；而随着含杂率的增加，物料推进速度则为先增大、后减小的变化趋势。因此，当需要提高物料推进速度时，可采用先增大回转半径，其次增大回转频率，最后增大筛面倾角的方法实现。针对物料推进速度来说，最优运动参数组合为A3B3C3D2，即回转半径、回转频率、筛面倾角均取高水平，而含杂率取中间水平。影响筛分效率大小变化程度的因素主次顺序为：因素D(含杂率)＞因素A(回转半径)＞因素C(回转频率)＞因素B(筛面倾角)，其中含杂率对筛分效率的影响程度最大，筛分效率随着含杂率的增大而增大的变化趋势，当含杂率达到4%时，筛分效率最高。当含杂率超过4%后，就会减少杂质接触筛孔过筛的机会，从而降低筛分效率。其次回转半径对筛分效率也有较大的影响，当筛体的回转半径偏小时，物料相对于筛面的运动幅度偏小，筛理路线变短，导致物料不能迅速的在筛面上散开，难以更好的分层，减少杂质接触筛孔的机会，从而降低筛分效率；当筛体的回转半径偏大时，则使物料相对于筛面的运动幅度偏大，导致推进速度过快，从而使应过筛的杂质颗粒不能接触筛面而不能过筛，降低筛分效率。对于筛分效率来说，最优运动参数组合为A1B1C1D2，即回转半径、回转频率、筛面倾角均取低水平，而含杂率取中间水平。

2 多指标优化矩阵分析

由于影响物料推进速度和筛分效率的两个评价指标的最优方案的结果不一致，而这些指标之间既相互依存又相互制约的关系，改变回转清理筛中任何一个运行参数，都会导致两个指标中的某个指标评价发生变化。于是，在单指标分析的基础上，引入矩阵分析法对两指标进行综合选优，并解决回转清理筛运动参数优化配置问题。

2.1 矩阵模型的建立

2.1.1构建指标、因素和水平层次结构

根据正交试验的仿真数据构建由指标、因素与水平构成的三层递阶层次结构模型，如图1 所示。

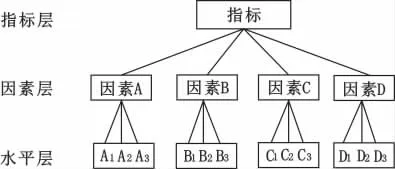
图1 指标、因素和水平层次结构

2.1.2构造层次分析评价矩阵

设多因素、多指标正交试验涉及到l 个因素，且每个因素取m 个水平，令j 表示第i 个因素取水平j时所得试验结果的算术平均值，且当试验评价指标要求是越高越好时，令aij=kij；当试验评价指标要求是越低越好时，令aij=1/kij，其中i=1、2、…、l，j=1、2、…、m。由此构建指标层评价矩阵，如式（2-1）。

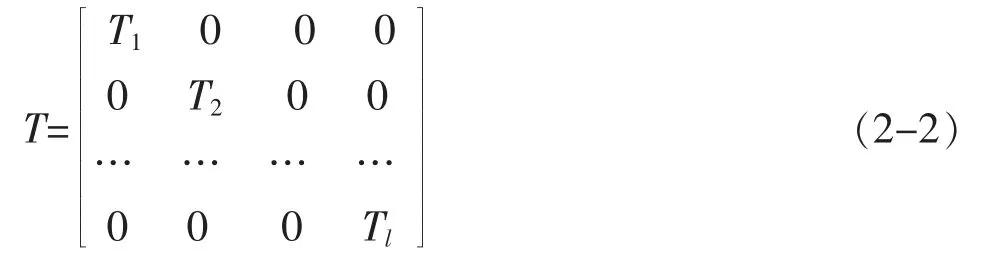
由此可得影响试验评价指标的权重矩阵，如式（2-4）

根据权重矩阵可计算出不同因素不同水平对评价指标影响的权重，并借助于权重分析得出最优的评价指标和各因素主次顺序[1-7]（数据计算见2.2）。

2.2 仿真结果的矩阵优化分析

根据矩阵分析模型，就第一个指标物料推进速度而言，由于评价指标要求越大越好，采用矩阵分析法优化，其权重矩阵W1计算过程如下：

由于第二个指标筛分效率，其评价指标也是越大越好，同理可计算W2为：

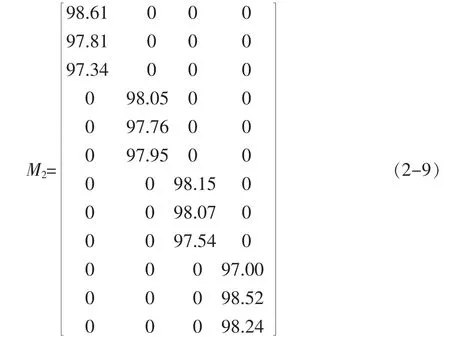
综合起来，多指标的总权重矩阵就是物料推进速度和筛分效率两评价指标的权重矩阵平均值，即：

由式（2-12）通过比较可知，因素A (回转半径)在三个不同水平下对评价指标物料推进速度、筛分效率的综合影响总权重分别为A1=0.1146、A2=0.1358、A3=0.1704，且A3的总权重最大；同理可知，因素B (筛面倾角)中B3=0.031 的权重最大，因素C(回转频率)中C3=0.0926 的总权重最大，因素D (含杂率)中D2=0.0834 的总权重最大。因此，依据总权重确定的回转清理筛运动参数的最佳组合方案选择为A3B3C3D2，即：回转半径25 mm，倾斜角度8°，回转频率7 Hz，含杂率4%。且各运动参数对评价指标影响的主次顺序为ACDB，即：回转半径＞回转频率＞含杂率＞筛面倾角。

3 结论

（1）回转清理筛工艺效果的评价往往涉及到多个指标，要求在正交试验设计中确保所有指标均能达到最好的效果几乎是不可能的。因此，为解决多指标的评价问题,一般是先将多指标的正交试验设计问题转化为单指标试验问题,并在单指标统计分析的基础上,根据各指标在整个试验中的重要性，衡量试验结果的优劣,并借助于矩阵分析的方法从定量的角度进行综合选优。所以本文所采取的方法是对解决粮食机械设备工作过程中多因素、多指标正交试验设计的优化问题的一种新尝试，此方法计算简单,分析过程严谨,所得结果具有很强的说服力,不失为粮食机械设备工作参数优化配置的一种非常有效的方法，具有一定的实际工程应用价值。

（2）在利用EDEM 等软件进行数值仿真模拟的基础上，采用多因素、多指标正交试验设计和矩阵分析法得到的回转清理筛运行参数的仿真数值模拟的优化配置结论：回转半径、倾斜角度、回转频率等运行参数在实际应用中可选择以高水平为设计依据，而含杂率既不能过高，也不能过低，保持适度的中间水平即可。

（3）利用矩阵法仿真分析得出的最优运动参数为：回转半径25 mm，倾斜角度8°，回转频率7 Hz。各运动参数对评价指标影响的主次顺序为ACDB，即：回转半径＞回转频率＞含杂率＞筛面倾角。