考虑需求和质量双重风险的动力电池回收定价策略和协调机制研究
2020-10-23赵梦园刘晨光
卢 超, 赵梦园, 陶 杰, 刘晨光, 余 江
(1.上海大学 管理学院,上海 200444; 2.上海理工大学 管理学院,上海 200093; 3.西北工业大学 管理学院,陕西 西安 710072; 4.中国科学院 科技战略咨询研究院,北京 100190; 5.中国科学院 大学公共政策与管理学院,北京 100049)
0 引言
随着新能源汽车产业的快速发展,动力电池装机增长迅速,也即将步入大量报废期。一般而言,动力电池的使用寿命为5~8年,2018年开始我国将迎来动力电池的报废高峰。根据中国汽车技术研究中心的数据,2018~2020年中国动力电池累计报废量将达到12~20万吨,2025年动力电池年报废量将增至42.2万吨。可见,如何妥善处理这些废旧动力电池已然迫在眉睫,而回收利用被公认为解决资源短缺、环境污染等问题的有效手段,受到新能源汽车产业界的普遍关注。
目前对于废旧动力电池的回收利用主要有梯次利用和回收拆解两种方式。梯次利用就是对废旧动力电池进行拆解、检测、分类、二次成组,根据电池的使用状况将其分档利用,应用于其它领域,充分发挥其剩余价值(陶志军&贾晓峰)[1]。据研究机构EVTank发布的《中国汽车动力电池回收拆解及梯次利用行业发展白皮书》预测,2020年我国动力电池回收拆解和梯次利用的市场规模将达到66.8亿元,其中梯次利用的市场规模远远大于回收拆解。由于从电动汽车上淘汰下来的电池仍有80%左右的剩余容量,如果直接进行回收拆解处理,将无法充分利用其价值,从而造成资源浪费。因此,诸如比亚迪、北汽新能源、格林美等一大批企业都加入了梯次利用市场,逆向供应链已经成为企业新的利润源。但是,采取何种定价策略、设计何种协调机制从而保障企业高效回收利用动力电池,尚未得到深入研究。
与正向供应链相比,逆向供应链所使用的产品或材料在获取过程中往往面临着高波动性,从而导致回收产品的数量和质量都具有风险(Denize[2];He[3])。目前,大多数文献主要聚焦于需求量和回收量的风险研究(Govindan et al.[4]),如Krapp et al.[5]提出了一种通用的预测方法来预测产品的回收量;He[6]考虑了在需求和回收量双重不确定下闭环供应链的定价和再制造决策,研究了供应和需求风险对供应链绩效的影响;韩小花等[7]研究了在成本和需求同时扰动下,闭环供应链系统中的最优生产决策与协调机制设计问题。可见,现有研究很少涉及到需求与质量的双重风险,但动力电池技术尚在发展当中,生产标准不统一,废旧动力电池的质量参差不齐,企业进行回收时必须考虑质量的风险问题,这对相关企业的定价策略和供应链协调带来了新的挑战。尽管不少学者对产品回收利用的定价问题做了较多的探讨,如Cai et al.[8]假设回收部件存在高质量和低质量两种情形,发现收购价格与获得的质量存在密切关系;高举红等[9]构建了需求不确定下再制造品和新产品存在竞争时的闭环供应链定价模型;闻卉等[10]考虑了专利保护下的定价决策;冯章伟等[11]利用Stackelberg博弈分析由第三方回收商领导的两级闭环供应链的回收与定价策略,但鲜有同时考虑需求和质量双重风险情形下的产品定价问题。此外,共享契约作为协调供应链的一种有效方式已得到了诸多学者的认可,如Govindan & Popiuc[12]认为在两级供应链和三级供应链中收益共享契约都能提高供应链的整体利润;李新然等[13]认为采用收益共享契约协调分散式决策闭环供应链可以有效应对突发事件的干扰;Inderfurth & Clemens[14]考虑了随机生产量和确定需求下的风险共享契约,但需求和质量双重风险大大增加了协调的难度。
基于此,本文构建质量和需求双重风险下的废旧动力电池回收定价模型并设计相应的协调契约机制,与现有文献相比有以下特点:(1)现有文献主要在单一风险下研究回收定价问题,本文将同时考虑来自市场的需求风险和来自回收渠道的质量风险,构建实现动力电池梯次回收利用的定价模型;(2)现有研究主要通过收益共享契约协调供应链,本文基于风险共享设计的完全补偿契约能够有效解决逆向供应链边际化问题;(3)结合具体算例探讨需求风险和质量风险对逆向供应链的影响,验证模型的有效性和先进性,从而拓展逆向供应链中产品定价策略和企业协调机制的理论方法研究,并为产业界提供参考。
1 动力电池回收定价模型
1.1 问题描述与假设
Savaskan[15]最早提出了制造商回收、零售商回收以及第三方回收三种渠道,为后续的研究奠定了基础。2018年2月底,工业和信息化部等七部委联合印发《新能源汽车动力蓄电池回收利用管理暂行办法》,明确了汽车生产企业作为责任主体,应建立动力蓄电池回收渠道,负责回收新能源汽车使用及报废后产生的废旧动力蓄电池。因此,本文亦按照此规定进行二级逆向供应链系统研究,并假设第三方平台负责维修和销售废旧动力电池。
本文考虑由一个汽车企业M和一个第三方平台R构成的二级逆向供应链(回收渠道),第三方平台R从汽车企业M处购买可梯次利用的废旧动力电池,维修后销往市场。当回收量不能满足第三方平台的订货需求时,第三方平台R将从供应商S处购买新电池。供应链结构如图1所示。
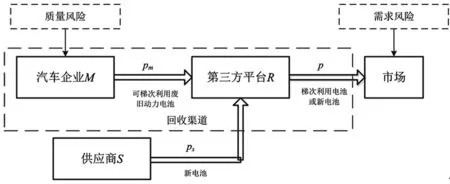
图1 质量和需求双重风险下的供应链结构
汽车企业M以单位回收价格r回收废旧动力电池,回收量L(r)是回收价格的线性函数:L(r)=ar+b(a>0)。经过检测后,回收的废旧动力电池将会分成两部分,剩余容量大于50%的动力电池可以被梯次利用,售卖给第三方平台R;剩余容量低于50%的动力电池进行回收处理,产生剩余价值v。

为了方便分析,本文做出以下假设:
假设1第三方平台R和新能源汽车企业M之间信息对称,均是理性参与人,都追求各自期望利润最大化。
假设2维修后的废旧动力电池和新电池质量功能相同,采用相同的售价p。
假设3电池供应商S有着稳定的供货能力。购买新电池的成本大于购买回收动力电池和维修动力电池的成本之和,即ps>pm+c0。
假设4不考虑第三方平台R和汽车企业M的仓储成本。
相关符号及其含义解释如表1所示:

表1 相关符号及其含义解释
结合动力电池的回收实践探索,本文构建一个两阶段的数学模型:第一阶段初,汽车企业M或第三方平台R制定回收价格r,在第一阶段末,得到回收量L(r)和可梯次利用量L(r)X;第二阶段初,第三方平台R根据可梯次利用量制定最优订货决策Q*,在第二阶段末,得到市场需求和利润。接下来,本文分别讨论分散决策和集中决策两种情形:分散决策下,供应链各成员基于自身利润最大化进行决策;集中决策下,基于供应链整体利润最大化进行决策。
1.2 分散决策模型
在分散决策的情形下,汽车企业M作为主导者制定回收价格r,第三方平台R制定最优订货决策Q*。在这一部分,将讨论确定需求和随机需求两种情形下的订货与回收定价决策。
1.2.1 确定需求下的分散决策
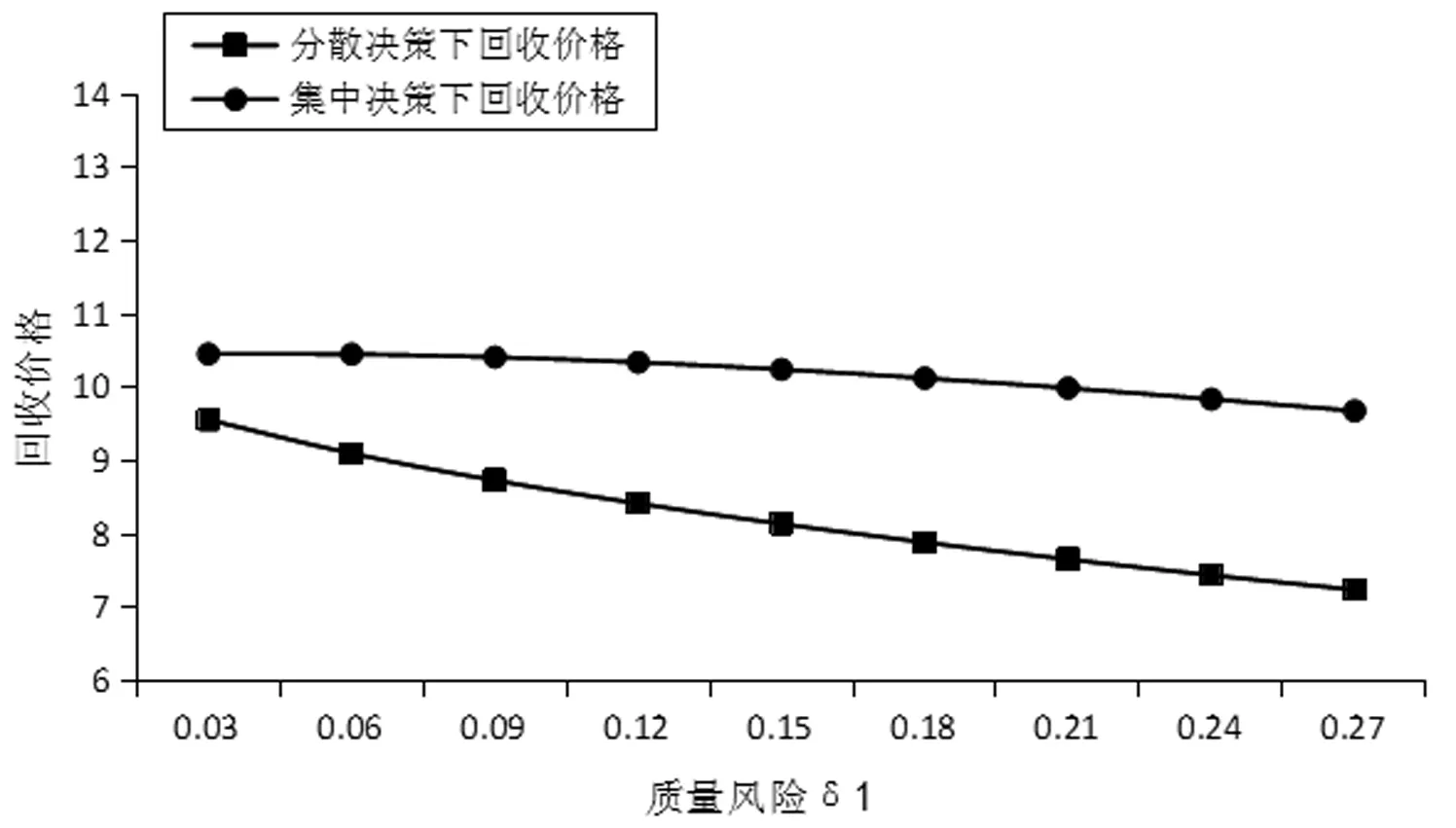
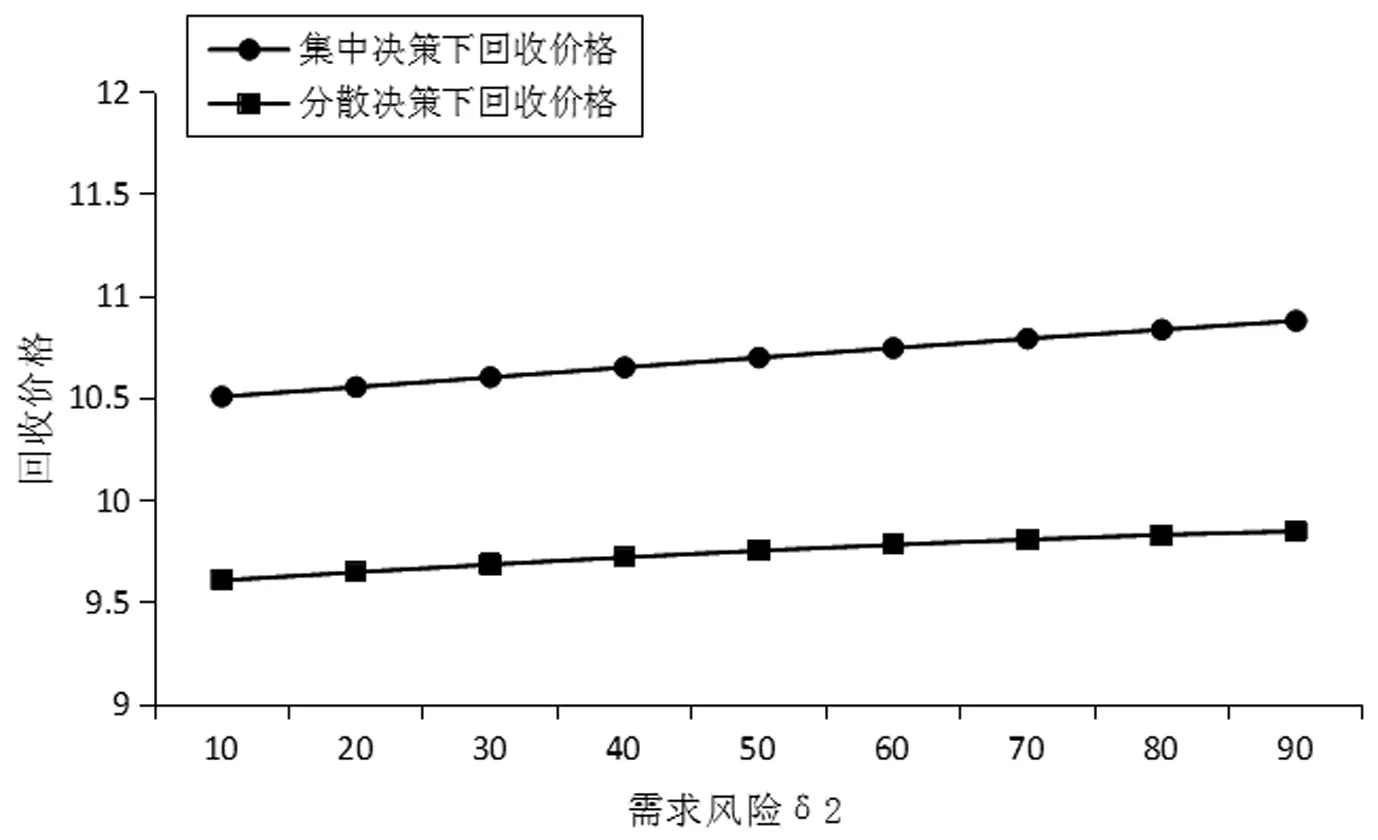
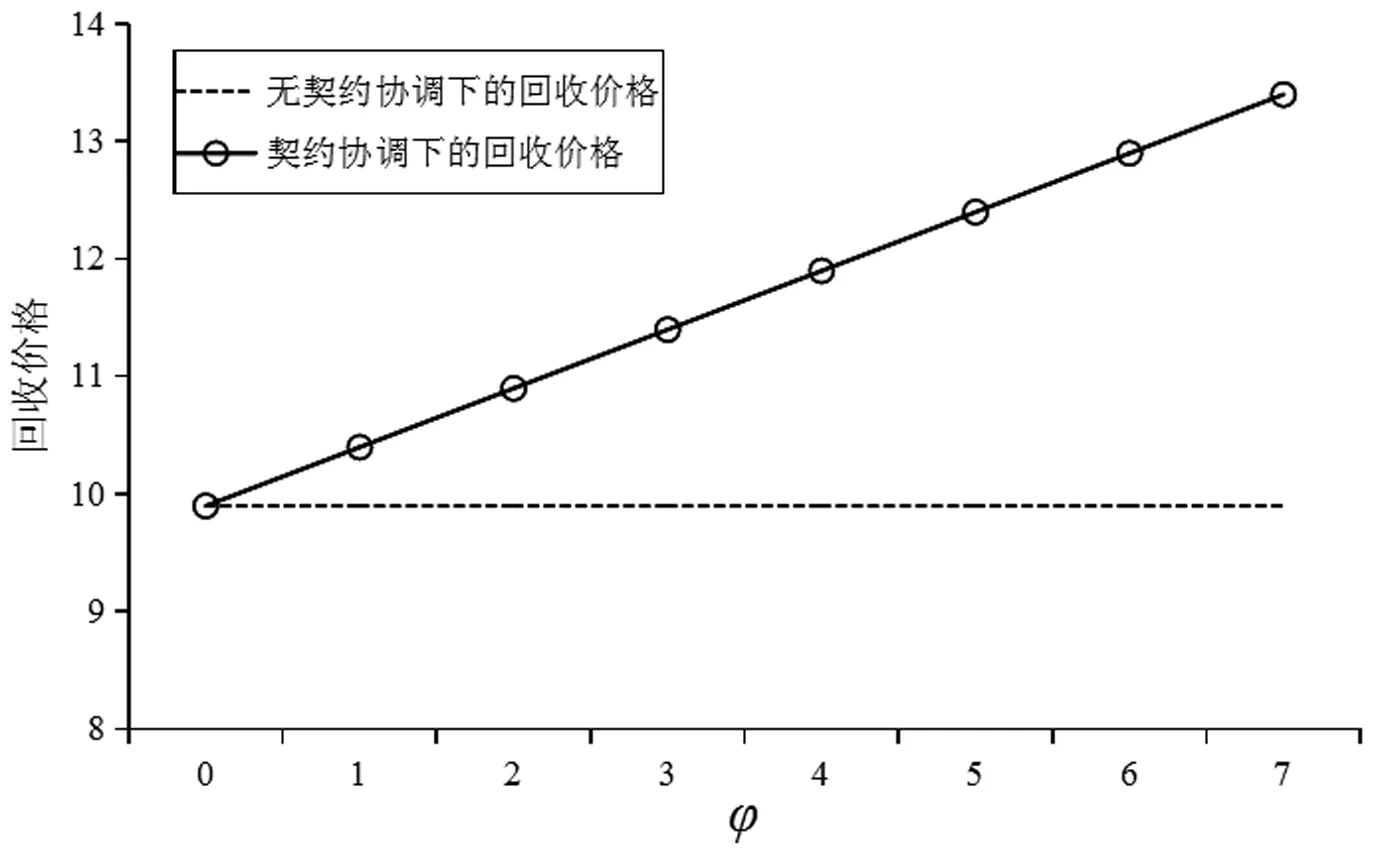
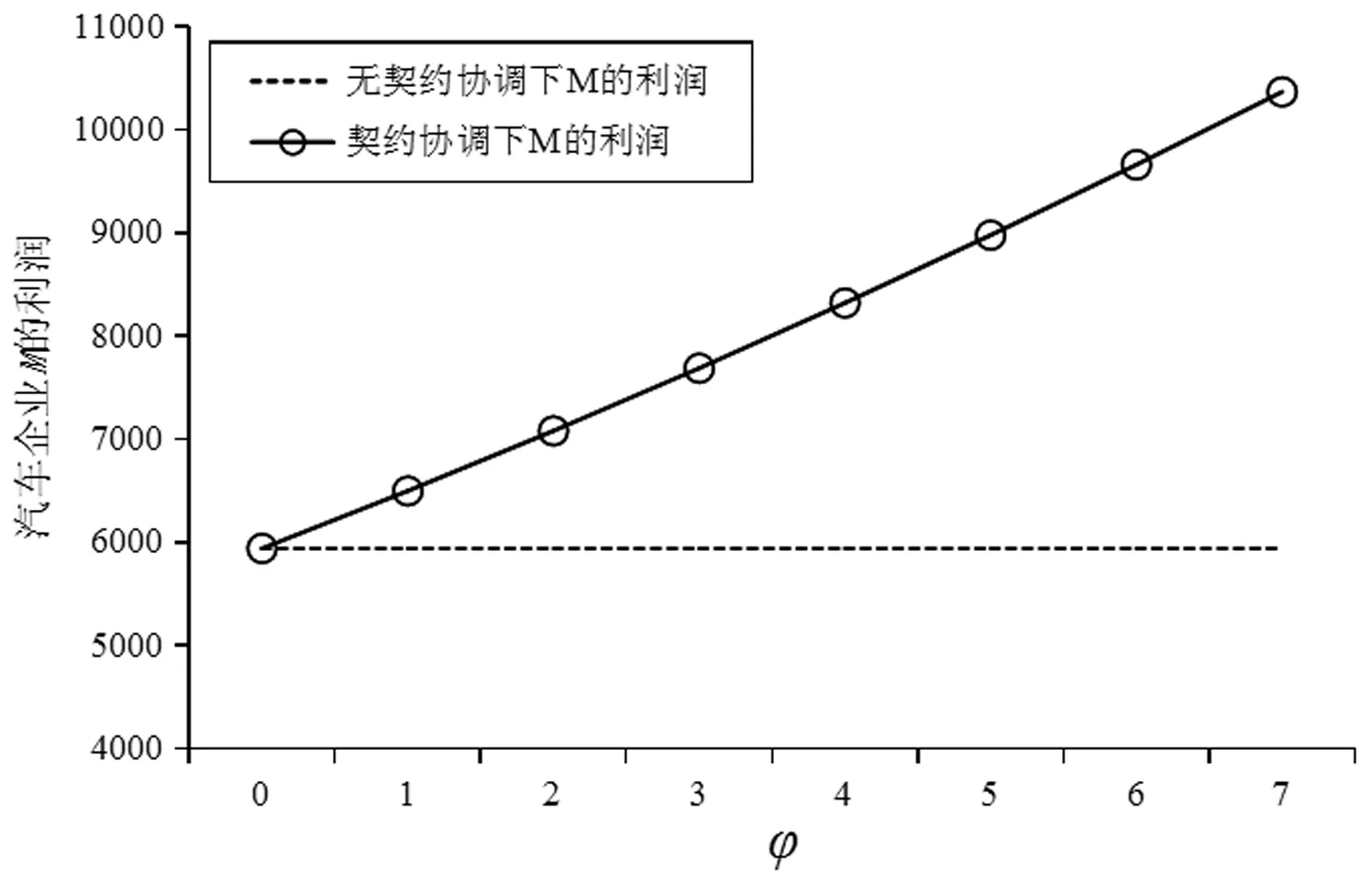
采用逆推法来确定双方的最优决策,首先确定第二阶段时R的订货决策。假设市场需求是确定的,用D来表示。此时,第三方平台R的最优订货决策Q*=D,当可梯次利用量能够满足市场需求时,即L(r)X≥D,第三方平台R将以pm的价格从汽车企业处购买D单位的废旧动力电池。当回收量不能满足市场需求时,即L(r)X pmmin{D,L(r)X} (1) 式中第一项为第三方平台的销售收入,第二项为维修成本,第三项为从供应商处购买新电池的费用,第四项为从汽车企业处购买可梯次利用废旧电池的费用。 在阶段一,汽车企业M的期望利润为: rL(r)-c1L(r)+vL(r)[1-E(X)] (2) 式中第一项为汽车企业的销售收入,第二项为回收成本,第三项为检测成本,第四项为回收处理废旧电池产生的剩余价值,E(X)表示期望可梯次利用率。 (3) 证明汽车企业M的期望利润可以扩展为: 对r求导: 证明由命题1得 推论1表明:在分散决策中,第三方平台提高购买价格pm,能够有效提升汽车企业的回收积极性,从而提高回收价格r和回收数量。 1.2.2 随机需求下的分散决策 第二阶段初,废旧动力电池的可梯次利用量L(r)X是已知的。因此,第三方平台R的期望利润为: ps[Q-L(r)X]+-pmmin{Q,L(r)X} (4) 式中第一项为第三方平台的销售收入,E[min{U,Q}]表示销售量为需求量和订货量中的较小值,第二项为维修成本,第三项为购买新电池的费用,第四项为购买废旧电池的费用。 命题2随机需求下,第三方平台R的最优订货决策有以下三种情况: (5) 此时,阶段一汽车企业M的期望利润为: (r+c1)L(r)+vL(r)[1-E(X)] (6) 式中第一项为汽车企业的销售收入,E[min{Q*,L(r)X}]表示第三方平台购买废旧电池的数量为最优订货量和可梯次利用量两者的较小值,第二项为回收和检测成本,第三项为回收处理废旧电池产生的剩余价值。 =L(r)+[r+c1-v(1-ε)]L′(r) (7) 证明对r求导,得 [r+c1-v(1-ε)]L′(r) 在集中决策的情形下,第三方平台R基于供应链利润最大化制定回收价格r。在这一部分,同样讨论确定需求与随机需求两种情况。 1.3.1 确定需求下的集中决策 在需求确定的情况,第三方平台R的最优订货决策Q*=D。可以得到第二阶段回收渠道的利润如下: (8) =pD-c0E[min{D,L(r)X}]- psE[D-L(r)X]+-(c1+r)L(r)+ vL(r)[1-E(X)] (9) 式中第一项表示回收渠道的销售收入,第二项为维修成本,第三项为购买新电池的费用,第四项为检测和回收成本,第五项为回收处理废旧电池产生的剩余价值。 =L(r)+[r+c1-v(1-ε)]L′(r) (10) 证明供应链的期望利润为: psE[D-L(r)X]+-(c1+r)L(r)+v(1-ε)L(r) [r+c1-v(1-ε)]L′(r) 推论2表明:集中决策下,逆向供应链的回收积极性较强,最优回收价格r*更高。这是由于独立运作时,汽车企业只考虑自身的利润最大化,面对质量风险更为谨慎,回收积极性降低。 1.3.2 随机需求下的集中决策 供应链将面对来自市场的需求风险,第三方平台R来制定最优价格以保证供应链整体利润最大。 命题5随机需求下,最优订货量Q*存在以下三种情况: (11) =L(r)+[r+c1-v(1-ε)]L′(r) (12) 证明阶段一时供应链的期望利润: psE[Q*-L(r)X]+-(c0+r)L(r)+v[1-E(X)]L(r) (c1+r)L(r)+v(1-ε)L(r) 对r求导: [r+c1-v(1-ε)]L′(r) [r+c1-v(1-ε)]L′(r) 由推论2可知,分散决策下逆向供应链存在双重边际化问题,有必要实施协调机制。由于回收质量和市场需求的双重不确定性,汽车企业M面临着供应过度的风险,即当D 在契约协调下,第三方平台R的期望利润为: pmE[min{D,L(r)X}]-φL(r) (13) 式中第一项为第三方平台的销售收入,第二项为维修成本,第三项为购买新电池的费用,第四项为购买废旧电池的费用,第五项为第三方平台R补偿给汽车企业回收废旧电池的费用。 汽车企业M的期望利润为: (c1+r)L(r)+vL(r)[1-E(X)]+φL(r) (14) 式中第一项为汽车企业的销售收入,第二项为检测和回收成本,第三项为回收处理废旧电池产生的剩余价值,第四项为汽车企业从第三方平台获得的补偿。 命题7在完全补偿契约的协调下,汽车企业M的利润函数在r上是凹函数,唯一最优解可由r′下式求出: =L(r)+[r+c1-v(1-ε)]L′(r)-φL′(r) (15) (16) 接下来讨论使得第三方平台R自愿履行契约的条件。 (17) 命题8表明:在满足一定条件下,第三方平台R和汽车企业M通过履行完全补偿契约,增加各自的利润,进而提高供应链整体利润。第三方平台R给予汽车企业M一定补偿,分担了质量不确定带来的风险,增强了汽车企业回收的积极性,促使其提高回收价格。进一步,增加的回收数量使得第三方平台更好地应对需求风险,利润得到提升。 为了进一步分析需求风险和质量风险对定价决策的影响以及协调机制的有效性,下面给出算例。 图2 质量风险下回收价格的变化趋势 图2表明,最优回收价格r*和质量风险成反比。分散决策下的最优回收价格较低,下降趋势更快,说明分散决策下供应链对于质量风险的抵抗能力较弱,集中决策能够提高供应链抵抗风险的能力。另外,集中决策时废旧动力电池的回收量较大,可获得更高的经济和环境效益。因此,汽车企业和第三方平台集中定价十分必要。 图3 质量风险下利润的变化趋势 由图3可知,汽车企业M的利润和质量风险成反比。说明质量风险损害了汽车企业M的利润,降低了M的回收积极性和回收价格,M在回收废旧动力电池的过程中应该注意管控质量风险。具体地,当δ1处于[0.03,0.15]时,第三方平台R的利润下降,M和R都有意愿加入协调机制应对质量风险。当δ1处于[0.15,0.27]时,第三方平台R的利润上升,说明质量风险较高时R从风险增加中获益;只有当接受契约带来的收益大于风险获益时,R才会遵守契约。综合图2和图3发现:随着质量风险增加,回收价格和供应链利润都呈下降趋势,这印证了质量风险下供应链存在双重边际化现象,有必要实施协调机制。 由图4知,回收价格与需求风险成正比,这种趋势与图2恰恰相反,说明可能是汽车企业M从需求风险增加中获益。 图5表明,随着需求风险增加,供应链和第三方平台R的利润呈下降趋势,R始终有降低风险的意愿,自愿履行契约。同时,为了应对需求风险,R往往会加大废旧动力电池的订购量,从而拉动M的销量上升,并进一步提高利润水平。需求风险下,M和R降低风险的意愿发生冲突,R应该加大对汽车企业M的补偿,当补偿大于M的风险获益时,M会参与到协调机制当中。 图4 需求风险下回收价格的变化趋势 图5 需求风险下利润的变化趋势 本小节参数与前两节参数一致,讨论双重风险下供应链利润的变化趋势。 图6 双重风险下供应链利润的变化趋势 图6表明,在双重风险的影响下,分散决策的供应链利润始终低于集中决策的供应链利润。分散决策时,质量风险和需求风险的增加都损害了供应链的利润。因此,在分散决策的情形下,综合改善两种风险能够显著提高供应链的利润。集中决策时,供应链利润随需求风险增加而降低,随质量风险增加先提高后降低。这说明,集中决策时综合改善两种风险未必能提高供应链利润:当质量风险较低,即δ1处于[0.03,0.15]区间时,只降低需求风险可以带来更高的利润;当质量风险较高,即δ1处于[0.15,0.27]区间时,考虑综合降低双重风险才能提高利润。 假设D=1000,完全补偿系数φ∈[0,7],其余参数与3.1节相同。 图7 协调机制对回收价格的影响 图8 协调机制对汽车企业利润的影响 图9 协调机制对第三方平台利润的影响 图7表明,回收价格与完全补偿系数φ成正比,说明协调机制有效地提高了汽车企业M的回收积极性。由图8可知,协调机制下汽车企业M的利润大于无协调机制下的利润,协调机制对M有效且M有意愿履行完全补偿契约。 图9表明,完全补偿系数在合理取值范围内,第三方平台R的利润会增加。当φ∈(0,φ1)时,R协调后的利润大于分散决策下的利润,R自愿履行契约;当φ>φ1时,R协调后的利润小于分散决策下的利润,完全补偿契约对R失效;当φ=3时,第三方平台R的利润最大,因此R选择给予M回收的废旧动力电池3单位价格的补偿。 结合图8和图9可知,当补偿系数φ∈(0,φ1)时,协调机制下第三方平台R和汽车企业M的利润大于无协调机制下的利润,完全补偿契约是有效的。协调机制实现了帕累托改进,第三方平台R和汽车企业M实现了共赢。因此,对于供应链管理者而言,需要合理地设置补偿范围,才能获得更大的收益。 本文构建了一个由第三方平台R和新能源汽车企业M组成的逆向供应链,分析需求和质量双重风险对分散式和集中式决策下闭环供应链定价策略的影响,并设计了一种基于风险分担的完全补偿契约协调机制来协调供应链,从而实现各成员的帕累托改进。主要研究结论如下:(1)相比集中决策,分散决策时的最优回收价格和供应链利润更低,逆向供应链存在双边际化现象,完全补偿合同能够协调供应链,实现供应链成员的帕累托改进。(2)质量风险较低时,对供应链成员都有损害,随着质量风险增加,回收价格降低,第三方平台R和新能源汽车企业M的利润均减少;质量风险较高时,R的利润随风险增加而提高,和M降低风险的意愿发生冲突。(3)新能源汽车企业M从需求风险中获益,第三方平台R的利润随需求风险增加而减少,二者降低需求风险的意愿存在冲突。 同时,本研究发现降低来自市场的需求风险和来自回收渠道的质量风险非常重要。其中,降低需求风险可以从两方面着手:(1)企业收集消费者的需求信息和设置安全库存;(2)政府通过补贴的形式促使消费者购买回收维修后的动力电池,从而积极推进动力电池的梯次利用。降低质量风险也可以从两方面着手:(1)企业对出厂的动力电池进行全生命周期监测,得出不同时期动力电池的剩余寿命,降低梯次利用时的质量风险;(2)政府部门尽快出台、完善动力电池回收利用的管理制度,形成科学的梯次利用及最终报废的回收体系。 本文主要验证双重风险对定价决策的影响,假设梯次利用产品和新产品的质量、价格相同。未来的研究中,要进一步考虑两种产品的质量竞争和价格竞争对定价决策和协调机制的影响。另外,本文只考虑了经济效益,综合考虑环境效益和社会效益,也是日后的一个研究方向。
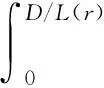
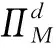
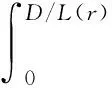
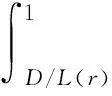
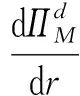
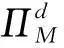
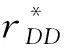
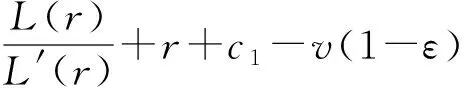
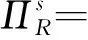
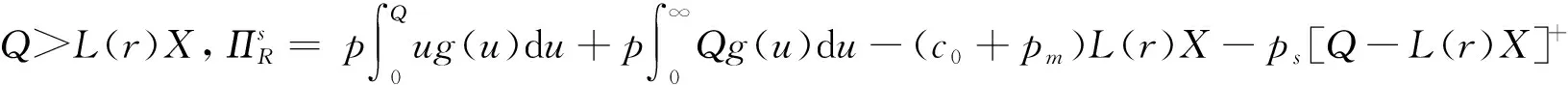
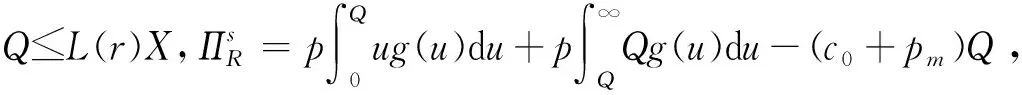

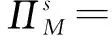


1.3 集中决策模型

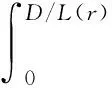
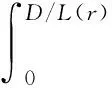
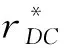

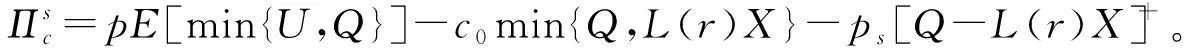
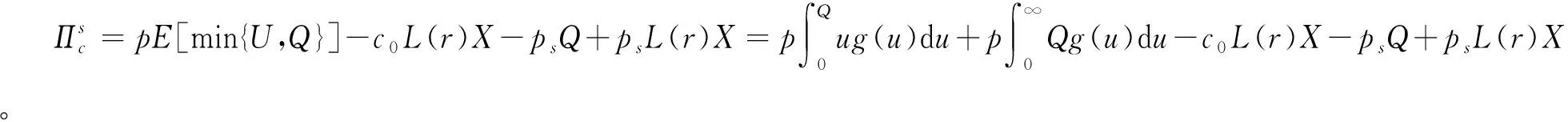

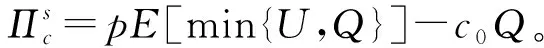


2 基于风险共担的契约协调机制设计
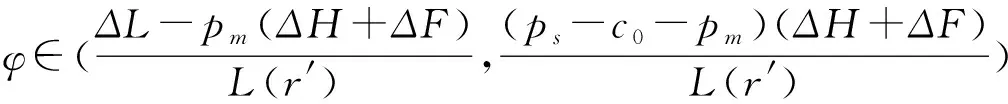
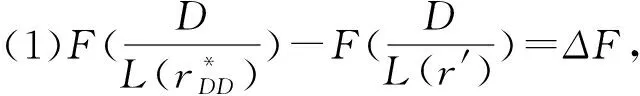

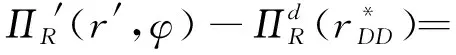
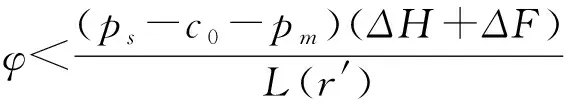
3 算例分析
3.1 质量风险的影响
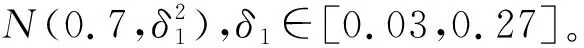

3.2 需求风险的影响
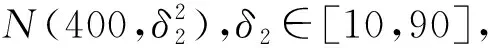
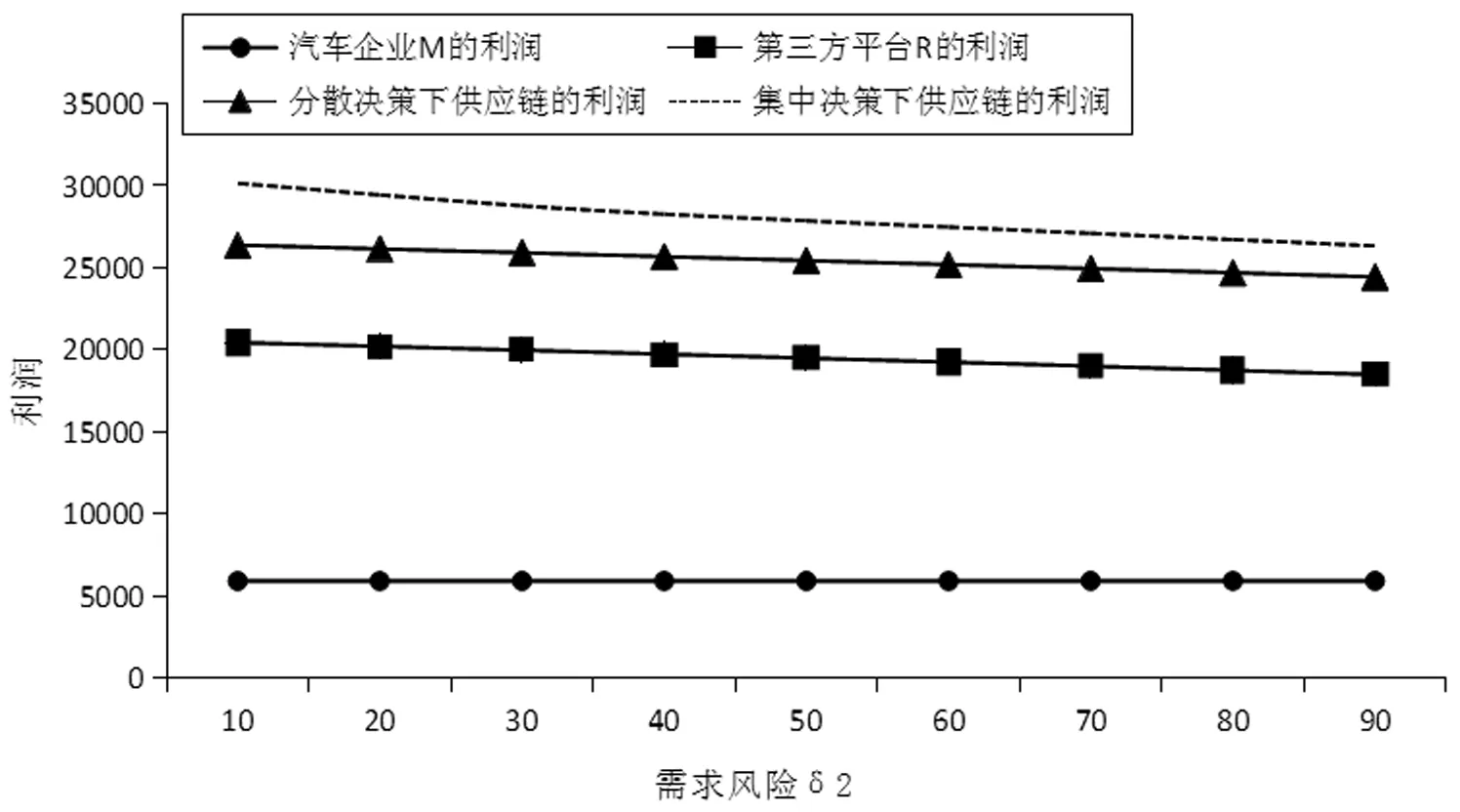
3.3 双重风险的影响

3.4 协调机制的影响

4 结论与建议
