考虑突发事件状态转移的政府应急物资采购定价模型
2020-10-23冯耕中扈衷权
刘 阳, 田 军, 冯耕中, 扈衷权
(西安交通大学 管理学院,陕西 西安 710049)
0 引言
我国是世界上遭受自然灾害最为严重的国家之一,2011~2015年我国有31个省(自治区、直辖市)的2800个县(市、区)频繁遭受各类突发事件(如洪涝、地震、泥石流等)的袭扰,造成年均全国3.1亿人次受灾,1500余人死亡失踪,900多万人次紧急转移安置,近70万间房屋倒塌,直接经济损失3800多亿元[1]。2018年8月受台风“温比亚”的影响,山东寿光发生特大洪水,造成了严重的洪涝灾害,共计有147万余人受灾,严重威胁着人们的生命健康与财产安全。突发事件发生后,应急物资(如帐篷、瓶装水、方便食品、棉被等)需求量呈现爆发式增长,政府首先将常规应急物资调拨至受灾区域。除此之外,政府还可以采取征用、调用等方式从应急物资供应商处获取可用的应急物资,投入救灾救援。但是,政府强制性的征用、调用应急物资不仅增加了灾后补偿成本,也没有考虑作为利润至上的供应商是否愿意为政府提供物资。突发事件是突发且随机的,绝大多数应急物资均有保质期,因此政府不可能储备无限量的应急物资。在我国,为了快速响应与有效应对突发事件,政府通常在灾前储备一定量的常规物资,在突发事件发生之初迅速将所需物资调度分配至受灾区域。除了紧急征用、调用所需物资外,政府还可以与应急物资供应商建立采购供应的契约关系,当储备的常规物资不足以满足突发需求时,可以从供应商处获得一定量的所需物资。随着《关于加强自然灾害救助物资储备体系建设的指导意见(2015)》和《国家自然灾害救助应急预案(2016)》的相继颁布实施,国家从政策上着重强调救援救灾物资储备方式的多元化,引导实现应急物资社会化储备机制,与供应商建立可持续发展的采购供应合作关系[2,3]。尤其是十九大后,国家发改委积极倡导完善健全市场机制,计划到2020年建成以“准许成本+合理收益”为核心的政府定价机制,不仅要求政府控制救灾成本,又要切实保障供应商的合理收益[4]。这就要求政府在储备有限常规物资的同时充分发挥市场机制的激励、约束作用,形成供应商与政府联合储备应急物资的模式。
数量柔性契约表示供应方允许采购方在知晓真实市场需求后,能够改变初始订购数量的协议,供应方有义务满足采购方可能采购的最高上限,防止采购方因为紧急增加采购数量而造成缺货损失。采购方也必须订购最低下限的产品,防止供应方因为过分高估需求而造成产能过剩。数量柔性契约在实现柔性供应、供应链协调以及减缓风险等方面优势明显,在应急物资采购管理中相比其他契约更具有适用性,因此本研究将数量柔性契约引入到政府采购定价应急物资的决策过程。突发事件状态总是不断发生转移,使得政府已经采购的物资在状态好转时容易造成浪费,在状态持续恶化时又不难以满足突发需求。基于此,本研究重点分析突发事件状态转移对应急物资采购定价策略的影响,构建政府主导的应急物资采购定价模型,推导政府和供应商之间达成契约合作的条件以及政企最优决策策略。
1 研究综述
从市场机制视角,探讨应急物资采购定价问题受到国内外众多学者的青睐,成为学术界的研究热点。国外学者主要从供应链管理角度展开研究,Arshinder等[5]利用契约实现了供应链成员共同承担风险与分享收益,建立图论模型,比较分析回购契约、收益共享契约与数量柔性契约的实施效果,最终根据供应链需求设计出合适的契约,供应链性能大大提升。Husain等[5]以马来西亚洪水灾害为例,提出了加强政府应急管理的框架,包括事前、事中与事后三个阶段的物资储备管理与分配。Chakravarty等[7]研究了不确定需求下的人道救援快速响应问题,提出两阶段方法:第一阶段,决策灾前应急物资储备地点与数量;第二阶段,决策灾后应急物资供应数量与时间。Lodree等[8]引入动态报童模型解决自然灾害引起的突发需求不确定性问题,通过分析应急物资供应不足产生的风险与收益,得到了应急物资最优库存水平。Taskin等[9]以预测的飓风规模为基础,建立了应急物资采购随机规划模型,确定了应急物资库存水平。
相比于国外基于市场机制的应急物资采购定价研究,我国政府通常在突发事件发生前储备一定数量的常规物资,并根据阶段性救灾成果作出采购决策,在该过程中探索实现政府与供应商双赢的采购策略或定价机制,是国内研究的热点。丁斌等[10~12]利用博弈论构建了政府和协议企业联合储备应急物资机制,解决了政企合作周期以及双方最优储备策略等问题。田军等[13~16]将不同类型的供应链契约运用到应急物资采购系统,通过分析政府和供应商之间的利益博弈,得出了政府最优采购量和供应商最优储备量。Hu等[17]利用期权契约构建了政府和协议供应商共同储备应急物资模型,不仅实现了应急物资供应链协调,而且推导得出政企双赢的条件。陈业华等[18]假设政府以实物储备物资,供应商以生产能力储备物资,构建了政府实物储备和企业生产能力储备模式下的应急物资采购模型,推导得出了政府最优实物储备量和供应商最优生产能力储备量。陈涛等[19]假设供应商可以以实物和生产能力两种方式储备应急物资,构建了实现供应商收益最大化的协调性模型,保证政府调整储备策略引导供应商以不同方式储备物资。梁樑等[20,21]利用期权契约构建了应急物资采购模型,求解得到了应急物资供应链达到协调且实现帕累托均衡的条件。
梳理文献发现,现有研究虽然取得了丰富的研究成果,但却存在一个强假设,即均假设突发事件状态不会发生转移,这与实际情况不太相符。现实情况下,突发事件状态总是不断发生转移,政府已采购的物资在状态好转时容易造成浪费,在状态持续恶化时又不足以满足突发需求,使得以往研究中的应急物资采购定价模型缺乏拓展性,在解决实际问题时难以广泛应用。换言之,对应急物资采购定价策略进行研究时,不单单要研究突发事件状态不变的情形,更要分析突发事件可能发生的状态转移情形对政企决策策略的影响。为此,本研究将数量柔性契约引入到应急物资采购供应链系统,分析突发事件状态转移情形下的政企利益博弈,构建政府应急物资采购定价模型,推导政企达成合作的条件以及双方最优决策策略。
2 问题描述
2.1 决策过程
突发事件发生前,政府与应急物资供应商签订一份数量柔性契约,并从供应商处以批发价格预先采购Q单位应急物资作为常规储备。除为政府提供Q单位物资,供应商还承诺为政府储备Q0单位应急物资作为柔性储备。如果突发事件发生,政府根据应急物资实际需求量(x),以预先制定的采购价格(p)从供应商处至多采购Q0单位物资。
假设突发事件在t0时刻以概率θ发生,其初始状态以及可能发生的转移状态包括三种类型S={S1,S2,S3}。S1表示x≤Q,政府储备的常规物资可以满足突发需求;S2表示Q
政府作为应对突发事件的核心责任主体,以博弈方 1 表示,策略空间包括:不采购柔性物资、采购部分柔性物资与采购全部柔性物资。突发事件以概率θ发生,以博弈方0表示,策略空间包括:S1、S2与S3。图1为政府与突发事件状态转移的博弈模型。第一阶段:突发事件在t0时刻发生,政府将常规物资调拨至受灾区域,在t1时刻突发事件状态发生转移,政府获得剩余物资残值收益的一步转移概率为p{xt1=S1};第二阶段:政府从供应商处采购柔性物资用于救灾,在t2时刻突发事件状态发生转移,政府需要进行柔性采购的二步转移概率为p{xt2=S1}+p{xt2=S2};第三阶段:政府额外补偿超出常规物资和柔性物资储备总量的部分,在t3时刻突发事件状态发生转移,政府需要承担缺货成本的二步转移概率为p{xt2=S3}。

图1 政府作为核心责任主体的博弈模型
2.2 基本假设
为了应急物资采购定价模型结果不失一般性,本文作出以下假设:
(1)政府采购的常规物资与柔性物资来源于同一个协议企业,即单一供应商。
(2)政企签订的数量柔性契约是单周期的,即契约时长与应急物资保质期相等。
(3)政府不能使用征用、调用等强制性手段从供应商处获取所需物资,此假设充分体现应急物资采购定价模型在市场机制下的价格效果。
(4)突发事件初始状态发生转移是有限次的,最多允许发生二步转移。
(5)S2与S3是互通的,S1为吸收态,此假设表明突发事件在S1会被有效控制。
(6)突发事件状态转移是平稳的,即m次转移概率矩阵等于一次转移的m次方。
(7)实际情况下,突发事件发生的持续时间远远小于救援救灾的时间,因此不考虑突发事件发生的持续时间对应急物资采购定价决策策略的影响。
2.3 符号说明与约束
x:应急物资实际需求量,服从随机分布,其概率密度函数和累计分布函数分别为f(x)与F(x)。
U:应急物资实际需求量的最大值,F(U)=1。
θ:突发事件发生概率,0<θ≤1。
Q:政府常规物资采购(储备)量。
Qd:政府应急储备库的最大库容量,Qd=Q。
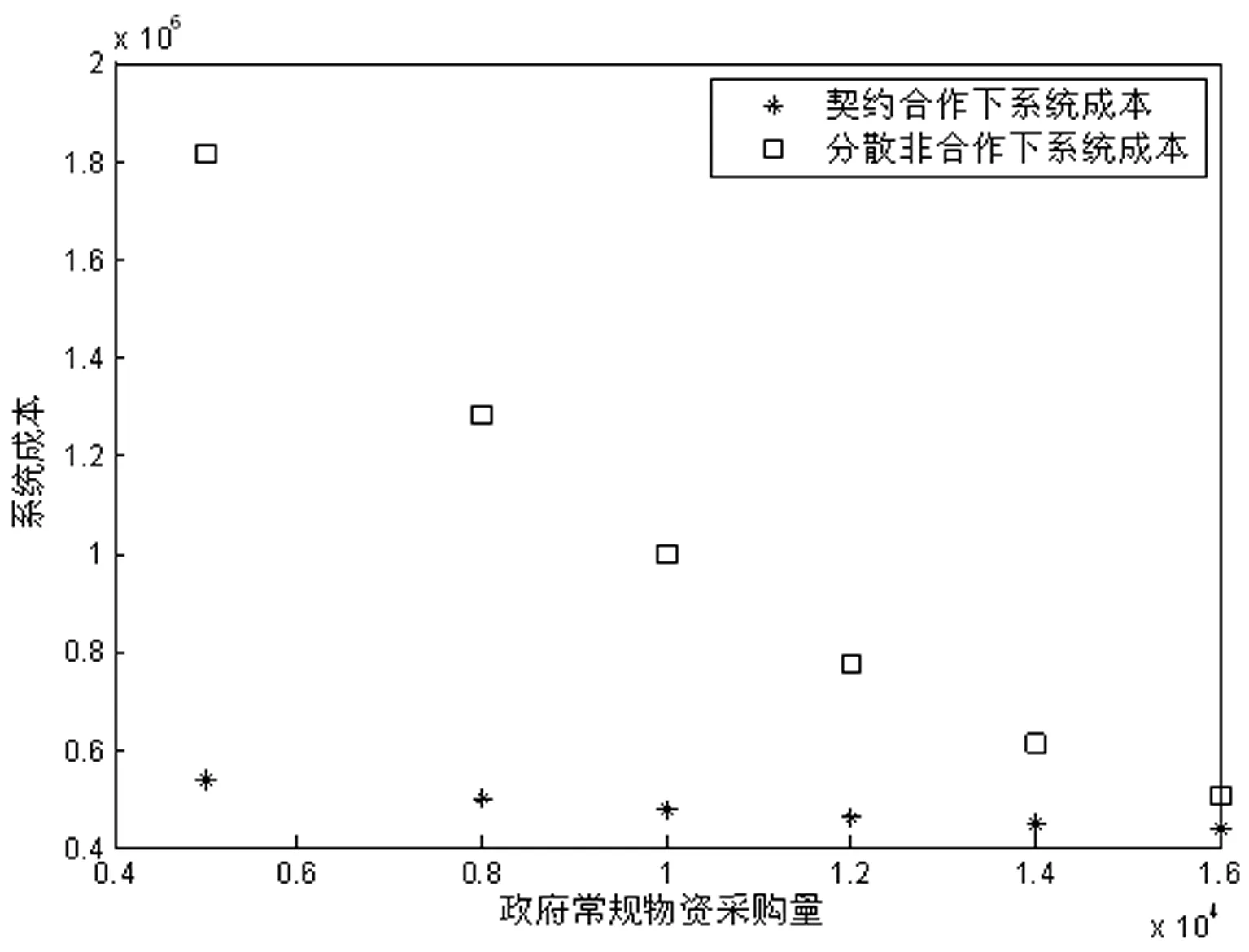
Q0:供应商柔性物资生产(储备)量,Q+Q0 c:供应商应急物资单位生产成本。 ω:政府批发常规物资的价格,c<ω。 h:单位物资库存成本。 v:剩余物资单位残值收益,v p:政府采购柔性物资的价格,p>ω。 M:单位物资缺货成本,M>p。 Si、Sj:突发事件状态,i,j=1,2,3。 Πsf、Πgf:契约合作下的供应商利润与政府成本。 Πsd、Πgd:分散非合作下的供应商利润与政府成本。 ΔΠg、ΔΠs:契约合作与分散非合作下的政府成本差值与供应商利润差值,ΔΠg=Πgf-Πgd,ΔΠs=Πsf-Πsd。 突发事件发生后,政府可以以预先制定的价格从供应商处采购一定数量约束范围内的应急物资,即应急物资采购是采购方决定的市场[20],因此存在政府主导、供应商从属的Stackelberg博弈关系,下面采用逆序推导法分析政企最优决策策略。 根据2.1节所示的决策过程,供应商产生的各类成本和收益包括三种情况: (1)在突发事件发生前,政府从供应商处采购Q单位物资储存在应急储备库,因此供应商从常规采购部分获得的收益为(ω-c)Q。除了生产常规物资外,供应商还需要为政府生产并代储Q0单位的柔性物资,因此供应商生产和库存成本为(c+h)Q0。 (2)如果突发事件在t0时刻以概率θ发生,供应商利润包括以下三种情形: 情形1突发事件状态经过一步转移后处于S1,一步转移路径包括{S1→S1}、{S2→S1}、{S3→S1},一步转移概率为p{xt1=S1},在此情形下政府不需要采购柔性物资,供应商获得剩余物资的残值收益为vQ0p{xt1=S1}。 情形2突发事件状态经过二步转移后处于S1和S2,二步转移路径包括{S2→S2→S1}、{S2→S2→S2}、{S2→S3→S1}、{S2→S3→S2}、{S3→S2→S1}、{S3→S2→S2}、{S3→S3→S1}、{S3→S3→S2},二步转移概率为p{xt2=S1}+p{xt2=S2},在此情形下政府从供应商处采购所需物资,供应商利润为(p(x-Q)+v(Q+Q0-x))(p{xt2=S1}+p{xt2=S2})。 情形3突发事件状态经过二步转移后处于S3,二步转移路径包括{S2→S3→S3}、{S3→S2→S3}、{S3→S3→S3},二步转移概率为p{xt2=S3},在此情形下政府需要采购全部的柔性物资,供应商利润为pQ0p{xt2=S3}。 (3)如果没有突发事件发生,供应商获得剩余物资的收益为vQ0(1-θ)。 综合上述,得到契约合作下的供应商利润函数,如(1)式所示: Πsf=Q(ω-c)-Q0(c+h)+vQ0(1-θ)+ (1) (2) (3) (4) (5) (6) (7) 综合考虑供应商储备决策、突发事件状态转移概率以及各项成本参数,政府制定采购所需物资的价格决策,供应商产生的各类成本和收益包括三种情况: (1)政府采购常规物资的批发成本和库存成本为Q(ω+h)。 (2)如果没有突发事件发生,政府获得剩余物资的残值收益为vQ(1-θ)。 (3)如果突发事件在t0时刻以概率θ发生,政府成本包括以下三种情形: 情形1突发事件状态经过一步转移后处于S1,一步转移概率为p{xt1=S1},在此情形下政府只需要从应急储备库调拨所需物资到受灾区域,并获得剩余物资的残值收益为v(Q-x)p{xt1=S1}。 情形2突发事件状态经过二步转移后处于S1和S2,二步转移概率为p{xt2=S1}+p{xt2=S2},在此情形下政府需要从供应商处所需物资,政府成本为p(x-Q)(p{xt2=S1}+p{xt2=S2})。 情形3突发事件状态经过二步转移后处于S2,二步转移概率为p{xt2=S3},在此情形下政府需要从供应商处采购全部柔性物资,并承担超出部分的缺货成本,政府成本为(pQ0+M(x-Q-Q0))p{xt2=S3}。 综上所述,政府成本函数如(8)式所示: Πgf=Q(ω+h)-vQ(1-θ)+ (8) (9) (10) (11) (12) 说明政府成本函数为p的凸函数,存在使得政府成本取得最小值的最优采购价格水平p*,求解(9)式等于零得到政府最优定价决策p*,如(13)式所示: (13) 分散非合作模式下政府依靠应急储备库储存常规物资,受到应急储备库最大库容量的限制,无法保证应急物资充足可用。除了承担常规物资成本外,政府还可能面临由于物资供应不足产生的巨大风险损失以及缺货成本。分散非合作模式下供应商依据已知订单生产并交付应急物资,不会进行柔性储备[22],因此供应商利润函数如(14)式所示: Πsd=Qd(ω-c) (14) 根据应急物资实际需求量,政府产生的各类成本和收益包括三种情况: (1)政府采购常规物资的成本与库存成本为(ω+h)Qd。 (2)如果没有突发事件发生,政府获得剩余物资的残值收益为vQd(1-θ)。 (3)如果突发事件发生,政府成本包括以下两种情形: 情形1突发事件状态经过一步转移后处于S1,一步转移概率为p{xt1=S1},在此情形下政府获得剩余物资的残值收益为v(Qd-x)p{xt1=S1}。 情形2突发事件状态经过二步转移后处于S1、S2和S3,二步转移路径为{S2→S2→S1}、{S2→S2→S2}、{S2→S3→S1}、{S2→S3→S2}、{S3→S2→S1}、{S3→S2→S2}、{S3→S3→S1}、{S3→S3→S2},{S2→S3→S3}、{S3→S2→S3}、{S3→S3→S3},二步转移概率为p{xt2=S1}+p{xt2=S2}+p{xt2=S3}=2,在此情形下政府需要承担的缺货成本为 2M(x-Qd)。 综合上述,得到分散非合作模式下的政府成本函数,如(15)式所示: Πgd=Qd(ω+h)-vQd(1-θ)+ (15) 已知Qd为政府应急储备库的最大容量,满足Qd=Q。从理性决策的视角来说,保证政企都愿意参与数量柔性契约机制的条件是政府成本与供应商收益必须得到改善,假设ΔΠg=Πgf-Πgd与ΔΠs=Πsf-Πsd,则需要满足不等式为: (16) 数量柔性契约机制与分散非合作模式下的政府成本差值如(17)式所示: (17) 数量柔性契约机制与分散非合作模式下的供应商利润差值如(18)式所示: (18) 当柔性契约机制下的利润大于分散非合作模式下的利润时,供应商才愿意为政府储备物资,求解(18)式大于零得出政府定价决策p*满足的不等式,如(19)式所示: (19) 政企双方无法达成契约合作的原因可能有:(1)政府常规物资储备量很大程度上可以满足突发需求,供应商为政府储备应急物资获益的可能性较小;(2)突发事件发生概率极小,参与契约合作机制反而导致双方利益受损;(3)政府从其他渠道获取所需物资相对容易,没有必要从供应商处采购物资,导致双方合作的积极性较低;(4)政府应急能力较强,能够有效应对突发事件并引导突发事件状态向易控方向转移,降低突发事件状态高危值,供应商获益可能性降低。 为了体现数量柔性契约在提高应急物资储备水平、降低政府成本以及保障供应商合理收益等方面的优势,下面将分析若干外生变量对政企最优决策策略与双方成本收益的影响,结合数值算例和敏感性分析进行解释说明,进而提出具有实践意义的管理启示。 突发事件发生前,政府以45元/件的批发价格从供应商处采购物资,然而突发事件发生后,政府需要以255.69元/件的高价从供应商处采购所需应急物资,主要原因可能有:(1)本文假设应急物资供应链系统中只存在一个供应方,使得应急物资市场的竞争性较弱而垄断性太强;(2)供应商为政府储备物资面临着无法售出物资的经营风险,因此只要政府制定的采购价格高于供应商能接受的最低价格且低于单位物资缺货成本都是合理、可接受的;(3)突发事件状态总是会不断发生转移,当突发事件状态高危值较低时,供应商获益较低,因此政府需要提高采购价格保证供应商参与契约合作。 4.2.1 政府常规物资采购量的敏感性分析 受到政府资金条件、应急储备库容量以及突发事件状态转移等因素的约束,政府在突发事件发生前从供应商处采购一定量的应急物资作为常规储备,这也是政企双方合作的基础。本节将对不同常规物资采购量下的政府与供应商决策策略进行敏感性分析,各项参数、决策变量、成本利润与系统成本如表1与图2所示。 表1 不同常规物资采购量下的敏感性分析数据表 图2 常规物资采购量对系统成本的影响 由表1与图2可以得出: (1)政府常规物资采购量越多,供应商售出预先储备物资的难度越大,增加了库存成本和不必要的浪费,因此供应商柔性物资储备量随着政府常规物资采购量的增加而减少。随着政府常规物资采购量的增加,供应商从契约合作中获得的利润增量逐渐变小,直到供应商柔性物资储备量为负值,政企双方不再合作。 (2)在同一常规物资采购量下,契约合作下的供应商利润大于分散非合作下的供应商利润,契约合作下的政府成本小于分散非合作下的政府成本。供应商利润与政府成本随着政府常规物资采购量的增加而减少,表明政府常规物资储备量越多越有利于政府控制成本,却无法保障供应商的合理收益,这是双方实现共赢的矛盾点。由此可见,政府采购适量的常规物资对于控制自身成本与保障供应商的合理收益至关重要。 (3)契约合作下的系统成本小于分散非合作下的系统成本,契约合作与分散非合作下的系统成本差值随着政府常规物资采购量的增加而减少,这是因为政府储备的常规物资越多越能有效满足突发需求,减少了由于物资供应不足导致的高额缺货成本。 4.2.2 政府单位物资缺货成本的敏感性分析 当应急物资实际需求量大于政府常规储备与供应商柔性储备的总量时,政府需要承担单位物资缺货成本,单位物资缺货成本越高表示政府获取应急物资的难度越大,本节将对不同单位物资缺货成本下的政府与供应商决策策略进行敏感性分析,各项参数、决策变量、成本利润与系统成本如表2与图3所示。 表2 不同单位物资缺货成本下的敏感性分析数据表 图3 单位物资缺货成本对系统成本的影响 由表2与图3可以得出: (1)供应商能接受的定价下限与单位物资缺货成本无关。当单位物资缺货成本较低时,政府最优定价水平低于供应商可接受的定价下限,因此供应商不能接受政府提供的契约,这是因为契约合作导致供应商利润受损。由此说明,数量柔性契约机制为供应商提供了自主决策权,一旦自身利益受损可以选择不为政府储备物资,是维护企业收益的重要方式。 (2)随着单位物资缺货成本的增加,契约合作与分散非合作下的供应商利润增量与政府成本增量逐渐增加,说明处置突发事件的难度越高,政府越需要提高采购价格促使供应商加大物资储备量,越能保证供应商的合理收益,却不利于控制政府成本,因此在政企契约合作模式下积极拓宽获取应急物资的渠道,是政府控制成本的有效措施。 (3)契约合作下的系统成本小于分散非合作下的系统成本,随着单位物资缺货成本增加,契约合作与分散非合作下的系统成本差值逐渐增大,这主要是因为应急物资短缺导致了高额缺货成本。 4.2.3 突发事件发生概率的敏感性分析 不同类型的突发事件的发生概率有所不同,政府需要制定相应的应急物资采购定价策略,本节将对不同突发事件发生概率下的政府与供应商决策策略进行敏感性分析,各项参数、决策变量、成本利润与系统成本如表3与图4所示。 图4 突发事件发生概率对系统成本的影响 表3 不同突发事件发生概率下的敏感性分析数据表 由表3与图4可以得出: (1)当突发事件发生概率很小时,供应商能接受的定价下限高于政府制定的最优价格,说明政企无法达成契约合作。随着突发事件发生概率的增加,供应商在契约期内售出所储物资的可能性增加,因此供应商会加大柔性物资储备量,供应商利润与政府成本相应增加。 (2)在突发事件发生概率同一水平下,契约合作相比于分散非合作增加了供应商收益,减少了政府成本和系统成本。随着突发事件发生概率的增加,契约合作与分散非合作下的供应商利润差值与政府成本差值增加,说明数量柔性契约机制对保障高发频发突发事件发生后的应急物资供应更有效。 4.2.4 突发事件状态高危值的敏感性分析 表4 不同突发事件状态高危值下的敏感性分析数据表 图5 突发事件状态高危值对系统成本的影响 由表4与图5可以得出: (1)当突发事件状态高危值较低时,政府需要提高采购价格以此保证供应商有利可图。当突发事件状态高危值超过一定水平后,供应商为政府储备物资的积极性大大提高,因此政府会降低采购价格。供应商物资储备量随着突发事件状态高危值的增加而减少,这是因为供应商降低自身储备量使得柔性物资被全部采购的几率增大,因此供应商利润增加。 (2)在同一突发事件状态高危值下,契约合作下的供应商利润大于分散非合作下的供应商利润,契约合作下的政府成本小于分散非合作下的政府成本,说明引入数量柔性契约机制对考虑突发事件状态转移的采购定价策略具有重要意义。 (3)契约合作下的系统成本小于分散非合作下的系统成本,随着突发事件状态高危值的增加,契约合作与分散非合作下的系统成本差值逐渐减小。由于性质恶劣的特重大突发事件状态经过转移后更容易具有较大的高危值,因此非常有必要引入数量柔性契约机制,对控制政府成本、保障供应商的合理收益以及降低系统成本的效果显著。 考虑突发事件状态转移的应急物资采购定价模型更加贴近现实条件,提高了应急物资保障能力的同时也避免了不必要的浪费,为落实应急物资采购和储备实践策略提供了依据,也丰富和扩展了应急物资采购理论与供应链契约理论。然而,本文只分析了政府与单一供应商构建的数量柔性契约机制,也没有分析现货市场对政企决策的影响,未来研究将从上述两点拓展应急物资采购定价模型。

3 模型建立
3.1 契约合作下的供应商利润分析
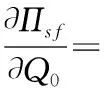






3.2 契约合作下的政府成本分析






3.3 数量柔性契约机制与分散非合作模式对比分析

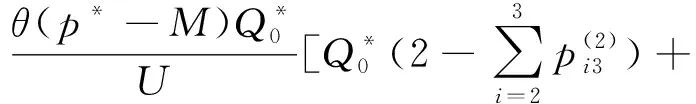



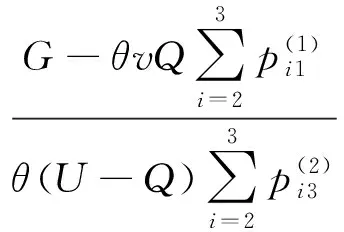


4 算例分析
4.1 案例描述与计算
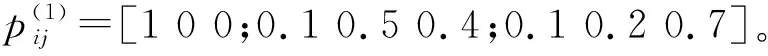
4.2 敏感性分析








5 结论

