轴辐式同城快递网络模式研究
2020-10-23李文莉李昆鹏阮文意
李文莉, 李昆鹏, 阮文意
(1.武汉纺织大学 管理学院,湖北 武汉 430200; 2.华中科技大学 管理学院,湖北 武汉 430074)
0 引言
随着科技飞速发展以及移动网络普及率迅速提升,电子商务的发展越发迅猛,这为快递行业提供了前所未有的发展机遇。为了更好地服务各地区人民,网点密度也愈加稠密化,城市乡镇的网点覆盖率也是逐步提升,在全国范围内已然形成了庞大的物流网络基础。同时,快递和人们生活的联系愈加紧密,同城快递的重要性也逐渐凸显,提供优异的同城快递服务体验也成了快递公司新的竞争点。X公司拥有健全的全国物流网络结构,以及竞争性的全国快递时效服务体验,但是其同城快递业务存在极大的时效提升空间。目前其同城快递网络结构主要有两种:一种是中转场模式即所有快件(不区分同城异地)集中运输到中转场,然后由中转场再运输至各个网点;另一种是点对点直通运输,快件流通量到了一定程度或者到了规定的送货时间,网点之间车辆直接对开,如图1所示。

图1 直通,中转场及集散点结构示意
第一种情况加重中转场分拣压力,造成资源的不必要重复浪费,同时增加时间成本。第二种情况一方面需要等待一定时间使快件达到一次运输标准,而同城快件客户一般对时间有明显预期,过长时间的等待容易造成客户流失,倘若优先考虑顾客服务时效则容易造成过大的运营成本;另一方面从资源本身而言大范围的点对点运输会使车辆运营成本居高不下。此外由于没有明确的网络结构划分容易导致管理运营难度提升,难以在客户需求激增以及有急切的时间要求的情况下做出即时高效反应。而物流网络结构优化一直是很多快递公司提升运营效率的方向之一,这同样适用于同城快递。通过借鉴全国的轴辐式物流网络结构提出了同城快递的集散点网络运营模式如图1所示,该模式的特点是将普通快件和同城快件加以区分,利用现有的网点资源,从中选择合适的网点成为集散点,搭建同城集散点网络结构服务同城快件。集散点针对的同城快件规模相对较小,无需对现有网点做出太大改变,只是在部分网点加入一个小型集散中转的功能,起到整合分配下属节点快件的集散作用。
轴辐式网络设计问题一般称为枢纽选址问题,重点是确定枢纽的位置以及给枢纽分配分支节点,最早由O’Kelly[1,2]提出。他在1986年首次将轴辐式物流网络结构应用到航空货运枢纽选址问题上,建立了多种选址模型,并指出该问题属于NP-hard问题[3];此后这个问题在学术上引起了广泛的关注。有些学者研究模型以及分配方式,比如Sohn[4]在文章中同时考虑了无容量约束的单分配和多分配的P-HUB选址问题,对P值固定时的两种情形建立了有效的模型和方法求解,有些学者研究在基础问题上进行相关的延伸,例如增加容量约束[5],非枢纽点的分支流向约束[6]。国内相关的研究较少,而且缺乏应用在同城快递上的相关研究。
本文依托快递公司同城配送的实际背景,在现有的单分配枢纽选址研究基础上研究了带枢纽点分支流向限制的枢纽选址问题,一定程度上填补了国内相关研究空白。此问题属于枢纽选址问题范畴,已被证明属于NP-hard问题[6],难以用精确算法快速求解,禁忌搜索算法是一种被广泛应用的启发式算法。傅少川[7]等研究了禁忌搜索算法在单分配枢纽选址的应用情况,此外禁忌搜索算法在相关文献中被证明求解此类问题可以得到较好的解[8,9],本文设计了相应的禁忌搜索算法对问题进行求解,算法加入了重启以及新的邻域搜索机制。最后验证了算法的有效性,并根据实验结果提出了管理上的建议。
1 问题描述与模型建立
本文研究的是带分支流向限制的单分配P枢纽选址问题在同城快递中的应用,模型的构建是在O’Kelly[10]提到的一般单分配枢纽选址模型的基础上增加枢纽点分支流向限制。同城快递网络可用G=(N,A)表示,其中N为所有节点的集合N={1,…,n},A为所有边的集合A={(i,j);i,j∈N,i≠j};每条边都有一个非负的长度Dij,且三点之间的关系满足三角不等式Dij+Djm≥Dim,∀i,j,m∈N。模型中Xijkm为两点之间的路径段的简略表示,其中i,j为路径的起点与终点,k,m分别为i,j所属的枢纽点,Xijkm所对应的路径段为Xij,Xkm,Xmj,且当取值均为1时,三个路径段共同构成了货物从i运输到j的流通路径,如图2所示。Cij为两点之间的单位运输成本,Cij与Xijkm的乘积为成本与下标对应的路径段组合的乘积,例如。(Cik+Ckm+Cmj)Xijkm=CikXik+CkmXkm+CmjXmj。在建模过程中不考虑车容量限制,且集散点之间运输存在折扣率。

图2 流向示意
1.1 参数设置
p:hub个数;a:干线运输的折扣系数;Wij:节点i与节点j之间的运量;S:可行路径集;S={(i,j,k,m):(k=i)∨(k≠i∧k=m=j)∨(k≠i∧k≠j∧m≠i)};Si′j′表示中S(i,j,k,m)中的i,j是固定值i′,j′;Si′j′k′表示S中i,j,k是固定值i′,j′,k′;Si′j′m′表示S中i,j,m是固定值i′j′m′。
1.2 模型设置
带枢纽点分支流向限制的单分配枢纽选址模型如下:
minZ=∑Wij(Cik+aCkm+Cmj)Xijkm
(1)
(10)
其中目标函数(1)是运输成本最小化,成本由快件量和运输费决定,因为主要是改变网点从属结构以及定义集散点功能,对整个网络及网点本身影响较小,故不考虑成为枢纽点的建设费用。成本由支线和干线运输成本决定,干线运输折扣率为公司一般规模效应产生的折扣率0.7;约束(2)表示枢纽点总数为p;约束(3)表示每个节点只能和一个枢纽点相连,是单分配枢纽选址的特点;约束(4)保证了只有枢纽点可以拥有下属节点;约束(5)和(6)表明了单分配这种结构模式的流向限制,非枢纽节点只可以和对应的枢纽节点相连;约束(7)为枢纽点分支流向限制,分支流向限制的主要是成为集散点的节点,因为普通节点主要对接节点只有集散点,而集散点面对的操作是将下属节点的快件聚集并根据快件流向进行分拣然后运输至其他集散点,以及将其他集散点运送过来的快件根据流向分拣后运送至其下属节点。当分支流向数过多的时候,集散点聚集过多快件,分拣时间相应的会增加,在人员有限的情况下,同城快件的时效得不到保证。根据mod动作法测算了分拣时间和流向的关系。单一流向分拣为0.3s,而每增加一个流向,分拣时间会增加0.08s来判断快件所属分拣方向,对于分拣员的规定是一小时处理500件可完成任务,则2.38s到2.4s一个快件,那么分支流向上限为26。又因为节点成为集散点,为了起到一个集散功能形成规模效应,下属节点数目大于4。约束(8)为枢纽点数目的范围。约束(9)~(10)为0-1变量。
2 优化算法
禁忌搜索算法是一种亚启发式随机搜索算法,通过设置禁忌列表避免陷入局部循环,被成功应用于多种学术问题求解上,在选址问题上也有不错的表现性能。本文采用禁忌搜索算法对问题进行求解,流程如图3所示,在处理过程中,通过对比多种算法的实验结果,以及将算法应用到不同数据集后,发现算法具有比较好且稳定的表现性能。相较于传统的禁忌搜索,本文提出的禁忌搜索算法设置了重启这一操作,会通过重启重新生成初始解,增加了跳出局部最优达到全局最优的可能性。优化搜索算法框架如下:
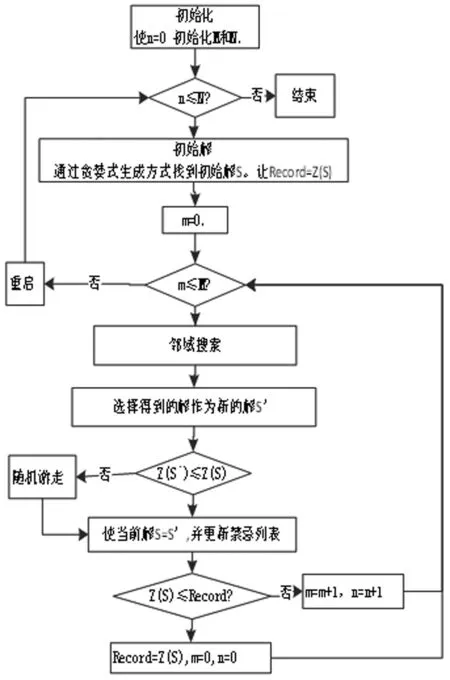
图3 算法框架
2.1 初始解生成
初始解质量的优劣对启发式算法效率有直接影响。常见的初始解生成方式有随机生成初始解,即根据约束条件限制,随机选择枢纽点,然后将非枢纽点随机分配给枢纽点,一般可以采用随机数,因为完全随机分配方式随机性太大,本文采用的禁忌搜索算法是针对一个初始解进行变化的一种启发式算法,所以初始解生成对算法表现有一定影响,本文初始解采用了部分随机的贪婪式生成方式。贪婪式生成方式即随机选择满足数量限制的枢纽点,这样可以增加算法重启时解空间的多样性,然后随机选择开始分配非枢纽节点的枢纽点编号,将与之相连最近的非枢纽节点分配给该枢纽节点,然后依次对其他枢纽点进行相应的操作,直到安排完成所有节点形成初始解。
2.2 邻域生成
邻域生成的方式在算法中起到至关重要的作用,对求解结果也有较大影响。在禁忌搜索算法执行时,对当前接受的可行解进行两种操作,一种是最优交换,这种邻域生成方式借鉴了遍历的思想,遍历所有非枢纽点移动至其他枢纽点的操作,以及所有的枢纽点和非枢纽点互换即0-1互换,选择最优移动或者互换执行;一种是随机0-1互换,随机选取非枢纽节点,使之和其对应的枢纽点进行互换。在执行操作时优先第一种邻域操作,当第一种邻域操作无法产生更好的解,则随机进行0-1互换,通过接受劣于记录的解来进行新的邻域搜索。
2.3 禁忌列表及藐视准则
由于传统的邻域搜索算法容易陷入局部最优的困境,禁忌搜索算法可以通过禁忌相关的移动来避免陷入局部最优。本文禁忌对象为禁忌出现过移动的操作,这里的移动一种是最优交换,一种是随机0-1交换。考虑到禁忌步长对算法的影响,在经过步长测试后,设置禁忌列表长为12。若某次操作出现当前最优解但是这次操作的变化点在禁忌列表中,操作也可以被接受,为藐视准则,此时接受这个操作并清空禁忌表。
2.4 评价函数及解的结构
根据目标函数,设定了新的评价函数来评判解的优劣。在进行每次操作选择时,根据操作造成的成本减小值进行衡量操作是否可被接收,优先选择使当前成本减少最大的操作接受,当减少值全为正数时会选择随机0-1交换。在构造算法时,将操作和对操作进行的成本减少的计算分开进行,选定最优操作之后才会对解进行变化,这样的处理方式可以提高算法的效率。在处理过程中对是否是枢纽点进行了判断和记录,并且使用另外的数组对枢纽点下属非枢纽节点进行了保存和记录,解的结构如表1所示,其中ishub记录节点是否为枢纽点,非枢纽点标为FALSE,枢纽点标为TRUE。solution记录解的结构,其中数组第1列记录的是枢纽点的标号,枢纽点之后记录的是枢纽点的下属非枢纽节点的标号。这样记录的好处是计算时可以清晰的表述以及找到枢纽节点和下属的非枢纽节点。
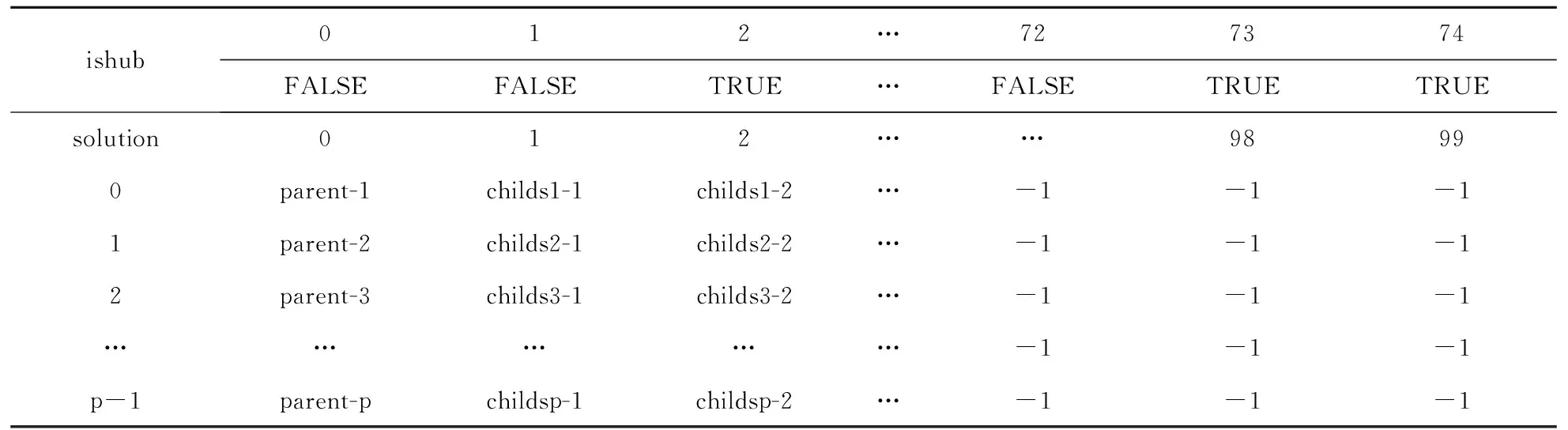
表1 解的结构
3 算例分析
该部分采用了两类数据分别进行实验,一类是传统的标准CAB数据集,CAB标准数据集是枢纽选址问题的经典测试数据集,主要包含了美国航空运输25个节点城市的流量和单位流量成本矩阵。因为本问题是在传统的枢纽选址问题中加入了一定条件限制,但是依然属于枢纽选址问题,所以将所设计的算法用于求解CAB数据并和已有的标杆结果进行对比来验证算法求解此类问题的有效性;另一类数据是采取X公司某地的同城快递业务一段时间的实际数据作为算例,使用设计的禁忌搜索算法以及前人研究中采用的一些算法对问题进行求解与对比。
3.1 经典CAB算例测试
因为传统的CAB数据集流量矩阵为上对称矩阵以及没有分支约束,和实际背景有一定出入,在对算法进行适当改编后,求解CAB数据集,结果如下表2所示,其中opt为标杆数值,TS为本文提出的禁忌搜索算法结果,PSO为找到的对比算法结果,其中PSO算法是由Yarpiz团队提供的开源算法。我们可以发现设计的算法可以达到前人研究所给出的标杆结果,具有很好的表现性能。部分结果优于标杆结果,比如20-3-1,20- 4- 0.2/0.6/0.8,25-3- 0.2/0.4,25- 4- 0.6,部分结果差于标杆结果,比如20-3- 0.4,20- 4- 0.4/1,25- 4- 0.2/0.4,在经过多次实验以及和其他已知算法对比,认为是因为计算本身精度原因造成,算法的表现正常。

表2 CAB标准数据集实验结果
3.2 基础对比实验
通过对比不同初始解生成方式对算法结果的影响以及禁忌表长度选择对求解速度和结果的影响并进行测算,为下文实际求解提供一定的支撑,测试数据使用的是枢纽点个数为10,折扣率为1的基础情况。全局最大未经优化的迭代步数(重启次数)为20,局部为1000。
3.2.1 初始解设置
对比随机生成初始解与贪婪式生成初始解两种方式对算法的影响来选择更利于求解的设定,其中随机生成方式是随机选取p个枢纽点,将剩余的非枢纽节点依次分配给枢纽节点。贪婪式生成方式即按照上文提到的初始解生成方式。表3所示结果为采用不同初始解生成方式下算法的运行结果,通过数据的对比可以发现不同的初始解生成方式对算法运行结果有一定影响,但是影响相对较小,在一定意义上采用贪婪式的初始解生成方式可以得到比较好的结果,且算法得到解的稳定性相较于随机生成初始解更好。随机和贪婪式差别较小也可以说明算法的搜索效率和收敛效率优良,可在一定的循环次数里采用任意初始解生成方式均可得到较优的解。
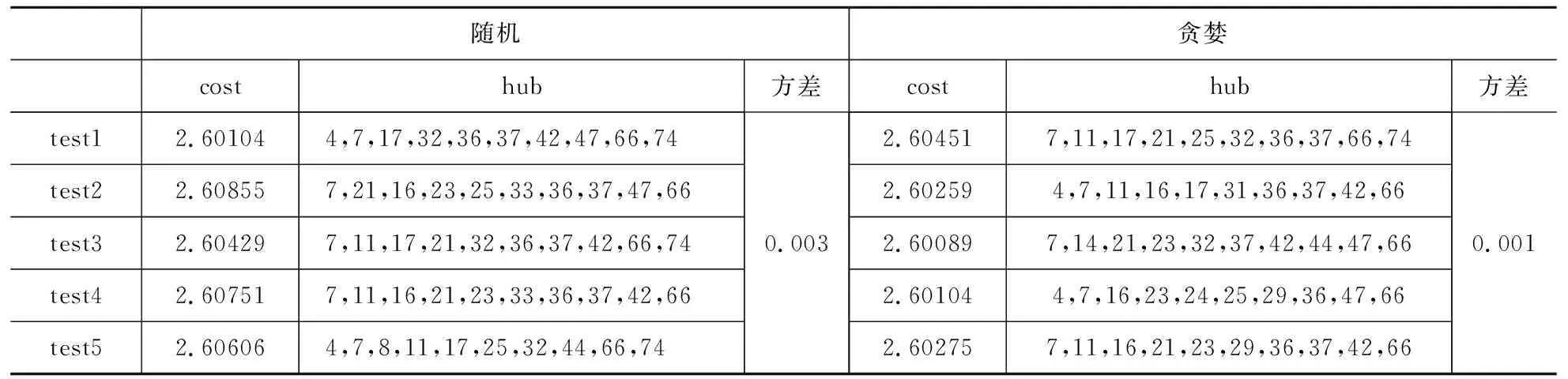
表3 不同初始解运行结果
3.2.2 禁忌列表步长设置
禁忌表长度对算法效率会有一定的影响,考虑到数据量和邻域规模,对禁忌表长度设置做了相应测试,因为本文存在重启机制,所以结果展示的是未经重启的第一次搜索结果,如图4所示,可以发现在长度4~22区间段,求解结果数值上有一定的区别,收敛速度也存在一定区别,图中最下方的虚线表现更好,说明禁忌表长度对算法的收敛性和搜索效果有一定的影响,在经过更多测试后发现,表长为12时,所得结果相对更为稳定,且在全局而言可以更快的得到质量较好的解,求解质量较好。所以在实验过程中使用的禁忌表长度取值12。

图4 禁忌步长测试
3.3 实际算例测试
根据目标函数的表达式以及相应计算方式可以直观的体会到枢纽点数目越多,整个网络成本越小。在经过基础实验后,根据分支流向限制的枢纽选址问题的模型和参数设置,分别测算了枢纽点个数在4~15时解的结构模式,为了增加得到更好解的可能性,全局未改善的循环次数设为100,局部未改善循环次数为1000。在测算过程中发现当枢纽点数目为15时,因为分支流向数目的限制,每个枢纽点的下属非枢纽节点数趋向平均,非枢纽节点的分配某种意义上是为了满足其分支流向的限制,求解意义变小,结构如图5示,可以发现在枢纽数每增加一个的前后对比中,部分枢纽点的选择相对固定,剩下的节点中因为需要产生新的枢纽点,结构发生改变,但是网络结构相对稳定。与此同时对比分析了PSO算法的求解结果,参数设置为1000个算子迭代2000次,惯性权重为1,惯性权重阻尼系数0.997,个体学习系数1.5,全局学习系数2.0,成本对比如表4,通过结果对比可以发现在本文问题求解上禁忌搜索结果远好于PSO算法结果。且在运行中PSO算法的求解速度远慢于禁忌搜索的求解速度。

表4 禁忌搜索和PSO求解结果比较


图5 枢纽点个数在4~15之间网络结构
3.4 实验结论
测算发现当不存在枢纽点时,运输成本为2.21565e+008,虽然运输成本较小,但是相应的对车辆投入会增加太多,在实际运营之中几乎不考虑全连通情况,一般若两点间快递量足够时,会采用小车进行两点之间直通运输,其余节点依然是运送至中转场进行统一转运。测算当存在一个枢纽点时运输成本为3.20245e+008,结构如图6所示,可以发现枢纽选择的位置位于整个图的中心区,但在实际运营中,枢纽因为面积等客观因素限制,所处位置几乎不可能位于中心地段,所以成本远大于模拟数值。
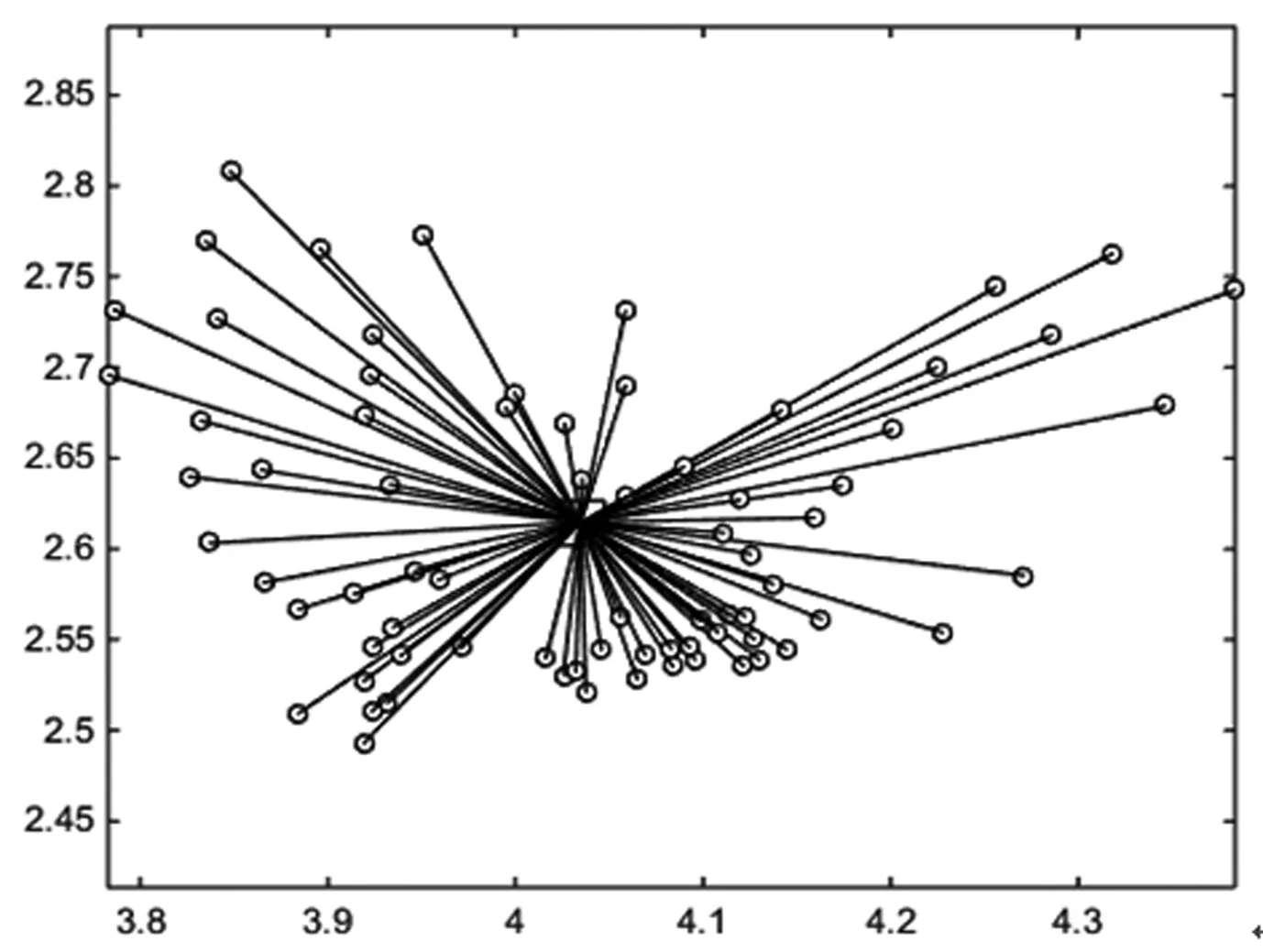
图6 枢纽点个数为1的网络

图7 无折扣分区

图8 折扣率为0.7时分区
通过算例实验给出不同数量下的集散点安排方式,且根据网络结构图,也可以更科学的对城市划分片区进行管理,而不是单纯根据区这一行政单位进行划分如图7,8所示,如何对城市网点进行管理也是快递公司面临的一大问题,这样的结构可辅助公司进行决策,进而提升管理效率。
4 总结
本文根据现实需求对城市物流网络结构进行设计,根据问题特性和学术研究中的枢纽选址问题相结合进行建模并求解,基于现实测算考虑了分支流向约束,设计了高效的求解算法得到高质量的解决方案,并且通过图形直观的展示。
根据实验结果认为将枢纽选址应用于同城快递网络结构设计中可以为同城快递分区管理提供科学依据。在采用集散点同城快递模式后,可在城内采取班车制度,定时的对同城快件进行转运以及配送,可以节省整个网络的成本。采用集散点模式后可以提升整个同城快件的时效,实现同城快递当日达,小时达等。之后可以进行的工作是将车辆路径问题与此问题相结合,设计相应的行车路线和时间表,将整个同城配送线路进行固化,方便管理,或者根据更具体以及一般化的要求对模型进行进一步的完善,例如加入其他在成本,工作量等更为具体的限制对选址进行进一步确定。
