基于系统固有特性参数在现场动平衡中的研究与应用

程英辉，吴立业

（1河钢股份有限公司承德分公司，2河北省钒钛工程技术研究中心，河北承德067002 ）

前言

振动是衡量旋转设备运行状态的一项重要指标，振动值越小越好。旋转设备产生振动的原因很复杂，其中以转子质量不平衡而引起的振动最普遍。常规动平衡方法步骤多，耗时长，利用系统固有特性参数实现现场动平衡一次成功,不仅可以缩短现场动平衡时间，还能提高转子在现场动平衡中的运行安全性。

1 系统固有特性参数推算

1.1 影响系数法具体步骤

以刚性转子、单面平衡为例，已知转子质量为M、直径为d、转速为r、角速度为ω，具体计算步骤如下：

第一步：转子在原始状态，启动至一定转速r时，测取被平衡的转子轴承原始振动的基频幅值和相位，即转子轴承座不平衡响应振动的幅值和相位，用表示，设°mm/s∠(°)，振动幅值为a0mm/s，相对相位为α0°。

第二步：已知试加重量为Wpg，假设相位为0°，试重P=Wp∠0°g∠(°)。

第三步：将加试重的转子启动到转速r时，测量转子轴承座振动基频振幅和相位，用矢量表示，设°mm/s∠(°)表示。

第四步：转子上应加的平衡质量及位置Q 由以下公式求得，设Q=Wq∠δ°g∠(°)：

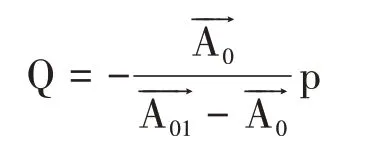
图1 单平面测相平衡法矢量图

1.2 确定配重块的具体相位

按照逆旋转方向测量配重块与光标的夹角β，按照图2 所示计算的配重块相位为β -∅，那么配重 块 用 Q=Wq∠(β -∅)g∠(°) 表 示。记 ∂=β -∅±180。

图2 振动传感器与键相传感器安装位置图（从电机看）

1.3 推算系统固有特性参数

转子不平衡响应振动（初始振动）、不平衡激振力（可以通过配重块的质量位置确定）、系统固有特性参数之间的关系[2]参照表1。

表1 转子不平衡振动响应、激振力和系统固有特性的关系

从以上关系中可以看出：转子不平衡振动响应与激振力成正比，激振力越大振动就越大，现场动平衡是解决激振力问题最快的途径。

2 风机现场动平衡实例分析

在转炉煤气回收系统中常用的是单级吸入悬臂结构的加压机：风机机壳为水平中分式、进风口位于水平轴向、出风口位于机壳上方、四盘角接触滚动轴承、转子部分由主轴和单级叶轮组成，如图3所示。

图3 加压机结构示意图

该加压机转速为2993.9 r/min,由于转炉煤气含杂质，需要每个月做一次现场动平衡。2019年12月11 日对该加压机做现场动平衡，过程数据如表2所示。

表2 用影响系数法现场动平衡数据

结合以上用影响系数法得到以上数据，根据转子系统特性参数的计算公式可以推算出该转子系统的固有特性幅值为6.73，相位为130°。

在2020年1月18日对该风机做现场动平衡，利用转子系统特性参数现场动平衡数据如表3所示。

表3 用系统特性参数现场动平衡数据

利用影响系数法对转子做完现场动平衡后的数据，推算出了系统固有特性参数。根据系统固有特性参数能实现现场动平衡一次成功。

3 结论

只要掌握了转子系统的 固有特性参数，测试出转子不平衡振动响应（初始振动），可以计算出不平衡激振力，即需要加的配重质量及相位，能够实现转子现场动平衡一次加重成功。该方法在实际工作中不受振动传感器、键相传感器及反光条的位置限制，可以极大提升转子现场动平衡的效果和安全性。