多种群灰狼算法优化ELM网络参数的研究

刘 彬，刘泽仁，李德健，王卫涛，刘浩然，闻 岩

(1.燕山大学 电气工程学院，河北 秦皇岛 066004；2.燕山大学 信息科学与工程学院，河北 秦皇岛 066004；3.燕山大学 机械工程学院, 河北 秦皇岛 066004)

0 引言

灰狼优化算法(Grey wolf optimizer,GWO)是一种基于群体搜索的新型智能优化算法，通过模拟自然界中灰狼群体等级制度和捕食行为达到优化算法的目的[1-2]。灰狼算法具有原理简单、参数设置少、易操作、寻优效果好等特点[3]，被广泛应用于函数优化[4]、传感器网络训练[5]、模型预测等领域[6]。但灰狼算法也存在种群多样性差、收敛精度不高、易陷入局部最优等缺点[7]。因此，为提高算法的精度和搜索性能，很多学者对灰狼算法提出了改进：龙文等[8]提出一种协调探索和开发能力的改进灰狼优化算法，算法利用佳点集的方法初始化灰狼个体位置，给出一种基于正切三角函数的非线性动态变化控制参数来协调探索和开发能力，改进后的算法能够有效协调其对问题搜索空间的探索和开发能力；Zhang S等[9]提出一种具有变异操作的灰狼算法，应用正交交叉算子和量化技术，通过统计最优解生成后代，从而增强算法的全局搜索能力，实现对多层感知神经网络性能的良好优化。目前这些单种群算法虽然在一定程度上提高了算法的搜索性能，但算法执行单种群的操作模式，会导致所有的灰狼个体趋向于同一种群的决策层，致使解的多样性降低，很难摆脱陷入局部最优的状态。根据间断平衡理论，有学者提出将算法单一种群拆分成多个子种群的方法[10-11]，采用多个子种群并行搜索：刘兵兵等[12]提出一种混合遗传算法，将遗传算法和单纯型算法结合，为避免算法陷入局部最优，引入实数编码，并采用多个子种群并行搜索，数值模拟表明该算法是有效的；孙漾等[13]提出了一种多种群竞争型协同文化差分进化算法，引入竞争策略及适应度评判标准，实现种群间的交流，提高了算法的多样性。张春燃等[14]对遗传算法提出改进，将单种群划分为4个子种群，并采用多交叉算子方式结合局部搜索方法对各子种群进行动态调整，有效提高算法的局部寻优能力和寻优速度。

极端学习机(Extreme learning machine,ELM)是由南洋理工大学黄广斌教授提出的一种针对单隐含层的前馈神经网络[15]。ELM算法随机产生输入权值和隐含层阈值，且在训练过程中无需调整，只要设置好隐含层神经元个数，便可得到唯一解，具有学习速度快，泛化性能好等优点[16-17]。但是，由于ELM输入权值和隐含层阈值取值的随机性，影响ELM的辨识精度和泛化能力[18]。因此，一些学者采用智能优化算法优化ELM结构参数：陈晓青等[19]提出改进的自适应混沌粒子群算法优化ELM参数，以增强算法的稳定性，提高ELM对基因表达数据分类的精度；Zhu等人[20]采用差分进化算法，利用结构简单的差分变异和交叉算子，并根据整个种群的动态调整来搜索最优的输入权值和隐含层阈值。

基于以上分析，本文提出一种改进的多种群灰狼算法(Multi-population gray wolf optimizer,MPGWO)，用以优化ELM网络结构的输入权值和隐含层阈值。算法根据间断平衡理论将单种群划分为多种群，并采用混沌序列初始化各子种群，提高灰狼搜索的遍历性。为避免算法陷入局部最优，对各子种群的决策层个体进行反向学习变异，并引入竞争策略实现子种群间的信息交流。将建立的MPGWO-ELM模型应用于篦冷机二次风温的预测中进行仿真实验。

1 多种群灰狼算法的构建

1.1 灰狼算法基本原理

灰狼以群居为主，在捕食行为中存在严格的等级制度，图1为灰狼等级金字塔。顶端的α，β，δ狼作为狼群的决策层，执行对猎物的追捕，其余的狼为ω狼，跟随α，β，δ狼对猎物进行跟踪围剿，最终完成对猎物的捕食。

在GWO中，假设在D维搜索空间中，第i个灰狼个体的位置为xi=(xi1,xi2,…,xiD)，i=1,2,…,N,N为种群规模。将种群中的个体按照适应度值进行排名，全局最优解记为α，次优解记为β，再次优解记为δ，其余个体记为ω。

狼群接近并包围猎物的数学描述如下[1]：

D=|Cxp(t)-x(t)|，

(1)

x(t+1)=xp(t)-AD，

(2)

式中，t为当代迭代次数；C为摆动因子；A为收敛因子；xp(t)表示猎物的位置；x(t)表示第t次迭代时灰狼个体的位置。摆动因子C和收敛因子A由式(3)和(4)决定：

C=2r1，

(3)

A=2ar2-a，

(4)

式中，r1、r2为[0,1]之间均匀分布的随机数；a为控制参数，其值随迭代次数递增从2线性递减到0，用公式表达如下：

a=2-2t/tmax，

(5)

式中，tmax为最大迭代次数。

当狼群确定猎物的位置并准备对其进行围捕时，决策层α，β，δ狼将带领ω狼展开捕猎行动。为模拟狼群的搜索行为，令所有的灰狼向每次迭代最优的α，β，δ狼学习。狼群捕食行为用数学描述如下[1]：

(6)

(7)

x(t+1)=(x1+x2+x3)/3，

(8)

式中，xα(t)、xβ(t)、xδ(t)分别为α，β，δ狼的灰狼位置；C1、C2、C3分别为α，β，δ狼的摆动因子；A1、A2、A3分别为α，β，δ狼的收敛因子。

1.2 混沌初始化多种群

GWO算法大多采用单种群模式进行搜索，所有的搜索过程都限制在一个种群内，通过一定的规则以“决策层”为中心不断向猎物靠近，如果个体趋向于一致，算法极易陷入局部最优。多种群算法是一种分布式进化算法，基于间断平衡理论，采用多种群进化能很好地降低算法陷入局部最优的可能性。本文拟采用将单种群划分为多种群的方法，考虑到若种群化分数量较少，将不能很好地探索整个解空间,解的精度比较低；若过多，则会增加算法的运行时间，使效率大大降低。本文受文献[14]启发，将单种群同样划分为4个子种群，每个子种群构成一个邻域，各子种群在各自所在的邻域进行寻优，对搜索空间进行全面探索。

在种群迭代进化之前，基本GWO算法的初始种群个体是随机产生的，这样可能导致种群的多样性差。另外，在解决实际问题时由于对待优化问题的最优解缺乏先验知识，在初始化种群时应尽可能使个体均匀分布在搜索空间中。

混沌是一种非线性现象，具有随机性、规律性及遍历性等特点[21]。利用其产生初始种群可使灰狼个体能够尽可能遍历整个搜索空间进行寻优，使算法具有良好的多样性。产生混沌序列的方式有很多，本文选用常用的Logistic混沌映射来初始化各子种群。用数学描述表达如下：

(9)

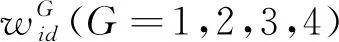
将混沌变量映射到待优化变量的取值区间范围内，即依次取i=1,2,…，N,便可得到N个初始种群个体。用公式表达如下：

(10)

采用混沌序列初始化各子种群，使灰狼个体能够均匀分布在搜索空间，尽可能遍历整个解空间，提高种群的多样性。

1.3 决策层反向学习变异

在整个狼群捕食猎物的过程中，决策层的α，β，δ狼起了至关重要的领头作用，其余的狼都会追随α，β，δ狼的搜索路径进行寻优搜索。因此，一旦α，β，δ狼陷入局部最优，整个种群的灰狼个体就很容易发生聚集现象，从而使算法陷入停滞状态。为降低算法陷入局部最优的可能性，本文对每个子种群的α，β，δ狼进行反向学习变异，使算法能够及时跳出局部最优，灰狼个体重新调整方向继续在整个搜索空间中探索。

反向学习策略是近几年来计算智能领域内出现的一种新技术[22]，已应用到了多种优化算法中。它的主要思想是，对一个可行解，同时计算并评估其反向解，从中选择较优的解作为下一代个体。

设在区间[a,b]上存在一个实数x，则x的反向数定义为x′=a+b-x。鉴于此，假设在R域上存在某N维点X=(x1,x2,…,xN)，并且xi∈[ai,bi]，定义X′=(x1′,x2′,…,xi′,…,xN′)为X的反向解。其中，xi′=k·(ai+bi)-xi，k为[0,1]之间均匀分布的随机数，称作一般化系数。

对每个子种群的决策层α，β，δ狼进行反向学习变异，会使灰狼的位置发生改变，变异后的灰狼位置用公式表达如下：

(11)

(12)

(13)

对各子种群起领导作用的个体进行反向学习变异，可带领其余灰狼个体在搜索过程中及时跳出局部最优，调整方向继续寻找最优解。

1.4 种群竞争及信息交流

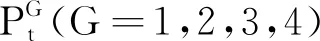
综上，本文采用混沌序列初始化各子种群，增强算法的全局搜素能力。并对各子种群决策层个体进行反向学习变异，以降低算法陷入局部最优的可能性。为实现各种子种群间的信息交流，引入动态竞争策略。将以上3种策略进行融合，有效改善了算法的寻优能力，提高了算法的收敛速度和精度，得到质量更好的解。根据以上对GWO算法进行的改进，构建了多种群灰狼算法，其结构如图2所示。

由图2给出MPGWO详细的优化步骤：

Step1:参数初始化:种群大小为4N，常数因子，最大迭代次数tmax，当前迭代次数t=1；

Step4:为避免算法陷入局部最优，根据式(11)～(13)对αG，βG，δG狼进行反向学习变异；

Step6：选择综合排名中最优的前3个灰狼α，β，δ灰狼分别更新每个子种群的决策层αG，βG，δG狼；

Step7：t=t+1；灰狼种群根据式(1)～(5)对猎物进行包围；

Step8：灰狼种群根据式(6)～(8)对猎物进行捕食，并更新灰狼个体的位置，跳转到Step3；

Step9：输出最终整个种群中最优灰狼个体α狼的位置，即为待优化问题的最优解。

1.5 MPGWO性能验证

为验证本文所提出的MPGWO算法的有效性，选取10个高维测试函数进行试验。测试函数的特征见表1，fmin为测试函数的理想最优值。其中，f1至f5为单峰函数，f6为带噪声函数，f7至f10为多峰函数，能够比较全面的验证算法的性能。并将其与PSO[23]、GWO[1]、融合多策略改进的HGWO[24]算法进行对比。

PSO、GWO、HGWO算法的参数按照相关参考文献进行设置；MPGWO算法种群大小设置为40，每个子种群大小则为10；最大迭代次数均设置为300。为有效减少随机性的干扰，每个算法均独立运行30次，计算测试函数最优值的平均值和方差，结果见表2。

表1 基准测试函数Tab.1 Benchmark function

由表2实验结果可知，GWO算法在10个测试函数中的表现几乎均优于PSO算法，表明灰狼算法在优化问题时具有更好的搜索性能，得到的解质量更好。MPGWO算法在10个测试函数上无论是平均值还是标准差相比于其他3种算法均具有明显的优势。具体来讲，MPGWO算法在f1、f2、f3、f6、f7、f8、f9函数上对比于其他3种算法在精度上有很大的提高，尤其在f1、f3、f7测试函数上的平均值相比其他算法更加接近理想值，说明MPGWO算法无论处理单峰函数还是多峰函数均具有明显的优势，这得益于MPGWO算法对各子种群决策层灰狼个体进行的反向学习变异策略，能够使算法及时跳出局部最优，增强算法的全局搜索能力。对于函数f9，HGWO算法和MPGWO算法均能够收敛到理论最优值0，而其他两种算法没有达到且距离理想值相差甚远。在4种算法中，无论测试函数是100维,500维，还是1 000维，MPGWO的优化效果整体上表现良好，且优势明显。同时从表中还可得出，在处理1 000维测试函数时MPGWO算法的优化精度基本上接近500维测试函数的精度，这在某种程度上说明，随着问题复杂程度的增加，MPGWO算法的优化效果并没有得到明显的减弱。在f4和f5测试问题中MPGWO算法的均值效果和方差均不如HGWO算法好，但是方差相近，说明算法在这两个测试函数中具有较好的稳健性。MPGWO在高维测试函数中均获得较好的寻优效果，说明对GWO算法的改进是有效的，多种群的划分和竞争策略的引入加强了种群间的信息交流，使灰狼个体尽可能遍历搜索整个解空间找到全局最优解。

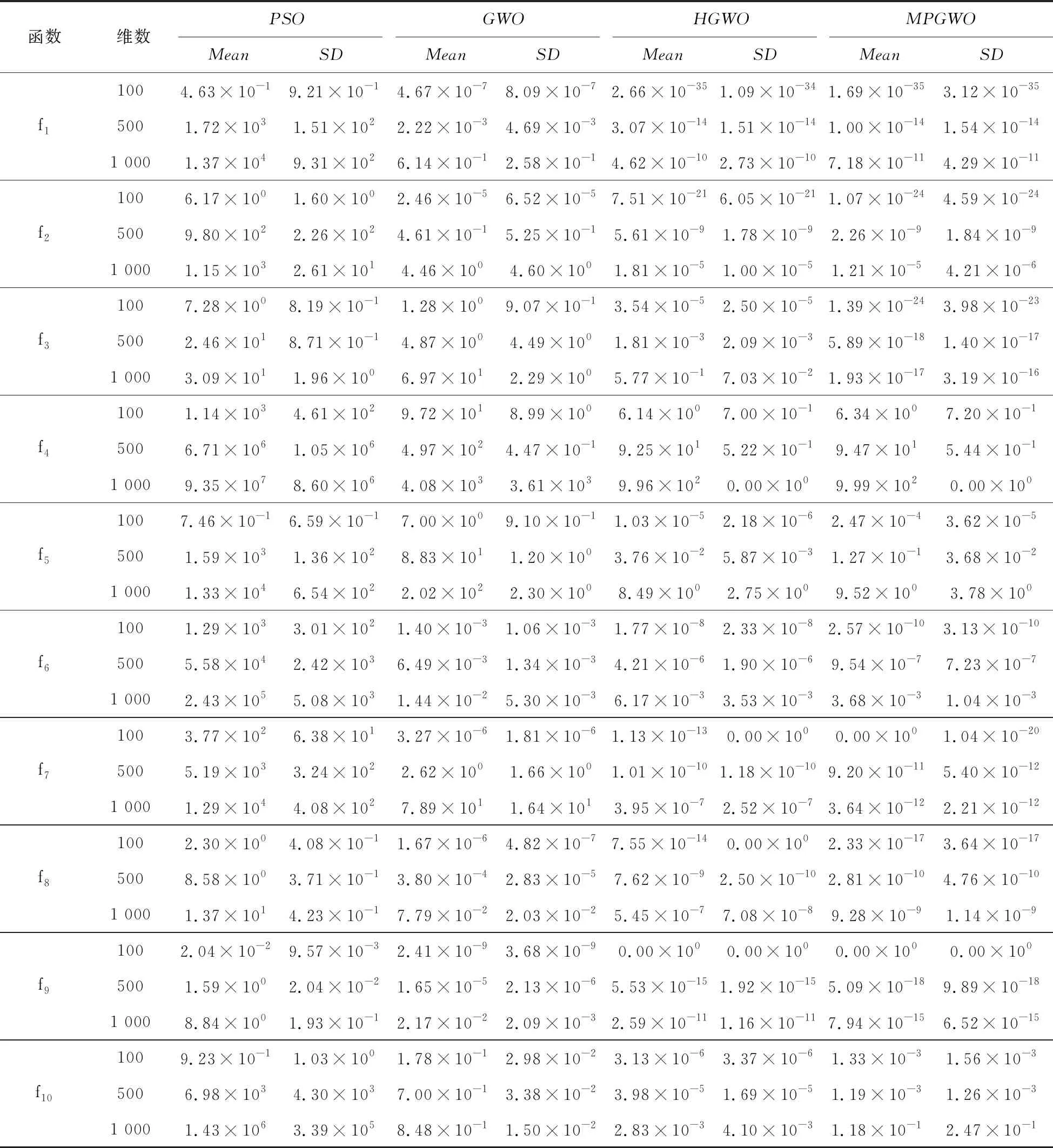
表2 4种优化算法性能比较Tab.2 Performance comparison of four optimization algorithms

2 水泥篦冷机二次风温预测模型

2.1 极端学习机

ELM是一种新颖的单隐含层前馈神经网络。其主要特点是：随机产生输入层与隐含层的连接权值及隐含层神经元的阈值[15]。输入权值和隐含层阈值一旦确定下来，则ELM的网络结构就随之被确定，变成线性系统，输出权值则可以通过最小二乘法计算得到。

极端学习机的输出Y用数学描述如下[15]：

(14)

式中，k=1,2,…,N，gj(·)为隐含层激励函数；W为输入权值矩阵；B为隐含层阈值矩阵；xk为输入变量；yk为输出变量；βj为隐含层输出权值；l为隐含层神经元个数；N为样本数目。

ELM的输出Y用矩阵形式表达如下[15]：

Hβ=Y，

(15)

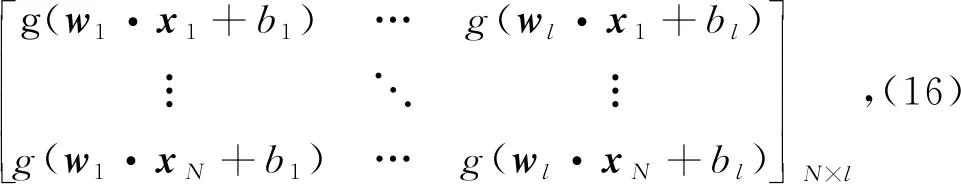
其中，β为输出权值矩阵，β=[β1,β2,…,βl]T；Y=[y1,y2,…,ym]T；H(W,B,X)为隐含层输出矩阵。

输出权值矩阵β可通过Moore-Penrose广义逆分析计算得出，过程如下[15]：

其中，H†是H的Moore-Penrose广义逆。

2.2 MPGWO优化的ELM模型

由2.1节可知，只要知道ELM模型中的输入权值和隐含层阈值，则ELM的网络结构也就被唯一确定。而ELM通常采用随机的方法给输入权值和隐含层阈值赋值，参数选取具有盲目性，这在很大程度上削弱了ELM模型的泛化性能。因此，为了降低参数选择对ELM模型的影响，本文采用MPGWO算法对ELM模型的输入权值和隐含层阈值进行迭代寻优，从而减小预测值和真实值之间的误差，强化ELM的泛化性能。

ELM模型参数优化过程中，灰狼个体搜索空间的维度D由ELM网络结构的输入权值和隐含层阈值个数决定；灰狼个体的位置取值范围则由ELM网络结构的输入权值和隐含层阈值的取值范围决定。灰狼个体的搜索过程即为对式(16)中的wj和bj(j=1,2,…,l)进行迭代寻优，然后求出隐含层输出矩阵H，进而根据式(17)确定唯一的输出权值矩阵β，然后将β代入式(14)计算模型预测值。建模过程的寻优问题为寻找使计算所得的预测值与真实值最接近的网络结构参数，用式(18)表示，也即整个种群中最好的灰狼个体α，其位置即为ELM网络结构的输入权值和隐含层阈值最好的取值。

在模型参数优化过程中，根据式(18)可将MPGWO建模过程的寻优问题表示为

(18)

图3为采用MPGWO算法优化ELM参数，从而建立MPGWO-ELM预测模型的流程图。主要思路为：采用MPGWO算法优化ELM模型的结构参数，以适应度值函数最小为原则，通过判断是否满足终止条件，将优化得到的参数代入ELM模型，便得到了MPGWO-ELM模型。

2.3 MPGWO-ELM预测水泥篦冷机二次风温

在新型干法水泥生产工艺过程中，二次风温主要由篦板推动次数、冷却风压和篦下压力等因素决定。因此，选取篦板推动次数(次/min)、冷却风压(Pa)和篦下压力(Pa)作为模型的输入，选取二次风温度(℃)作为输出。从某水泥厂生产线DCS系统历史记录中共筛选500组样本数据，随机选择其中400组作为训练样本，其余100组作为测试样本。MPGWO算法参数设置同1.5节参数设置。模型中参数设置为：输入变量维数n=3；隐含层神经元个数l=100；预测输出变量维数m=1；训练次数为30。

训练数据的实际温度与模型预测输出值对比图如图4所示，从图中可知预测输出值逼近真实曲线，即模型训练预测输出值与实际二次风温度逼近。

为验证本文提出的预测模型的有效性，分别与ELM、PSO-ELM、GWO-ELM、HGWO-ELM进行对比，对水泥篦冷机二次风温度进行预测。采用100组测试数据的实际输出与模型预测输出对比曲线如图5所示。

比较5种方法水泥篦冷机二次风温预测效果图可知，随机赋值ELM结构参数的模型真实值和预测值拟合程度较差。PSO-ELM、GWO-ELM、HGWO-ELM预测值和真实值拟合度相对较好，说明采用智能优化算法对ELM结构参数寻优使模型的预测精度和泛化能力有很大的改善。MPGWO-ELM预测输出能够准确反应二次风温度的变化趋势，虽然当实际输出温度出现较大波动时，预测输出存在偏差，但在误差允许范围内。另外MPGWO算法优化的ELM比PSO、GWO、HGWO算法优化的ELM曲线拟合度好，表明改进的GWO算法具有更好的寻优能力。

为进一步仿真实验5种模型的建模质量，采用均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)及平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)作为性能测试指标，如式(19)～(21)：

(19)

(20)

(21)

如式(20～21)所示，训练数据和测试数据与MPGWO-ELM算法所用数据相同。ELM的结构参数采用随机化的方法；PSO-ELM、GWO-ELM、HGWO-ELM的结构参数为相应智能优化算法优化的结构参数；算法隐含层节点数均为100；隐含层激励函数均为Sigmoid函数；输出层函数为线性函数。对比结果如表3所示。

表3 不同模型的性能指标对比Tab.3 Comparison of performance indicators of different models

由表可知，ELM网络的辨识误差最大，均方根误差达到9.132 8，这是因为算法采用随机化的方式选取结构参数。对比ELM和PSO-ELM两个辨识结果可知，采用PSO算法对ELM的输入权值和隐含层阈值参数进行优化，能够有效提高模型算法的辨识精度和辨识的准确性。从GWO-ELM、MPGWO-ELM两个辨识模型可以得知本文改进的MPGWO算法显著由于基本的GWO寻优能力。相较于融合多策略改进的HGWO算法，本文改进的MPGWO算法优化得到的模型，辨识精度更准确。

3 结论

利用间断平衡理论将灰狼算法的单种群划分为多个子种群，并采用混沌序列初始化各子种群，提高了算法的多样性。为降低算法陷入局部最优的可能性，对各子种群的决策层个体进行了反向学习变异。为进一步加强算法的寻优能力，引入竞争策略选择整个种群的最优决策个体，并动态实时分享到各子种群，实现了各子种群的信息交流，提高了算法的全局搜索能力。将改进的MPGWO算法与PSO、GWO、HGWO算法进行对比，仿真结果验证了MPGWO算法拥有较强的搜索能力和稳健性。利用MPGWO算法对ELM网络结构的输入权值和隐含层阈值进行优化，建立MPGWO-ELM预测模型。然后，采用MPGWO-ELM预测模型预测水泥篦冷机二次风温度，实验结果表明其辨识精度和泛化能力均高于其他四种对比方法。对二次风温的准确预测可以使现场操作员根据二次风温度值调整生产参数，对水泥生产具有重要的理论和实际意义。