消防水炮射流轨迹理论模型研究

王 储，袁晓明,*，杨志刚，孟昭亮，孙 靖

(1. 燕山大学 河北省重型机械流体动力传输与控制重点实验室，河北 秦皇岛 066004；2. 先进锻压成形技术与科学教育部重点实验室(燕山大学)，河北 秦皇岛 066004)

0 引言

伴随着社会的进步和经济的发展，大型商场、体育馆、飞机场和高层住宅已成为城市建筑的重要组成部分。与此同时，这些大空间和高层建筑对消防安全提出了严峻的挑战。为提高灭火的快速性和准确性，不仅要在第一时间瞄准火灾点进行射流，而且对不同流量、不同俯仰角情况下的射流轨迹进行准确定位至关重要[1]。

目前，对于射流轨迹的定位研究主要有两种方式：一是运用计算机图像技术对射流轨迹进行定位，其优势在于可以形成闭环控制，实现渐进式的控制和调节，控制精度较高；二是根据质点运动规律通过数学计算预测射流轨迹，其优势在于只需根据水炮俯仰角和流量等参数便可简便快捷地预测射流轨迹。

对于第一种方式，Alcan Gokhan等提出应用粒子阴影尺寸技术对泡状射流进行监测，通过改进固体粒子图像分割算法实现对射流微元的精确分割[2]；陈静等提出了一种基于最大类间方差和区域生长相结合的消防水炮射流轨迹分割与识别算法[3]；王冬月等针对弱对比度射流利用红外图像的特殊性质对其进行轨迹定位[4]；Han Seo Ko等采用四维数字散斑成像技术对高速氦射流进行分析，并使用三台高速CCD摄像机从多个角度对射流轨迹进行捕捉[5]；针对消防水炮轨迹识别中的射流分叉、高亮度背景和背景晃动等问题，赵敏等提出了基于多轨迹矢量搜索的射流轨迹识别方法[6]，搜索出各射流轨迹后，根据先淘汰后择优，逐级筛选的思路提出一种分步骤逐级筛选寻优方式[7]，并将粒子群算法与之融和[8]，大大提高了射流轨迹搜索识别的准确性。对于第二种方式，Xu Qiang等基于局部最大平均速度建立了指数形式的射流中心线轨迹方程，研究了射流动量比和雷诺数对湍流射流流场的影响，预测结果的误差在30%以内[9]。胡国良等近似认为对于炮口初速度不高的水射流，其空气阻力与空气阻力系数和速度乘积的一次方成正比，并通过积分运算得出射流轨迹曲线方程[10]。Ma Ji等基于射流传播假设，提出了一种计算浮力气体射流轨迹的数学方法，与实验结果的误差均小于10%[11]。Wu Jianhua等针对仰射射流在射出瞬间会卷入部分空气，使其所受空气阻力更为复杂的问题提出了融入偏转角的综合阻力系数，经验证射程最大误差仅为8.6%[12]。针对小流量水炮射流轨迹的预测，闵永林等将俯仰角融入空气阻力公式，计算结果表明模型中射程相对误差均小于4%。在对压缩空气泡沫射流轨迹的研究中，胡成等通过在已有轨迹曲线方程中添加计算修正系数的方式使预测精度满足要求[13]。

综上可知，上述两种射流轨迹预测方式具备各自优势，但均有待于进行深入研究，从而对射流轨迹进行更加准确的预测与定位。考虑空气阻力数学模型的多种变化因素，通过添加修正系数的数学计算方式对射流轨迹进行预测所需硬件设备较少，且计算速度较快。拟对消防水炮射流微元体进行受力分析，结合牛顿第二定律、外弹道学和空气阻力模型等理论，对射流微元体的角加速度和整体射流截面面积变化情况进行修正，以期提高消防水炮射流轨迹预测的准确性，并通过实际射流轨迹对所建立模型进行验证。

1 射流轨迹理论模型

以单位质量微元体为研究对象，水射流主要受到重力和空气阻力的作用。由于射流过程发生在地球表面附近，可认为重力加速度保持不变，因此重力不发生变化。一般认为空气阻力与速度的平方成正比，与射流微元体的速度方向相反且共线，但由于实际射流过程中破碎现象的发生，会导致空气阻力与过流断面的法线方向偏离一定角度。图1为射流微元体受力分析示意图。

图1中v为射流微元体的速度，θ为速度方向与x轴的夹角，Ft为空气阻力，与速度反向偏离一定角度，mg为微元体所受的重力，方向竖直向下。

设i为速度方向的单位矢量，则

v=vi

(1)

两端对时间进行微分，则

(2)

其中

(3)

式中，j为垂直于速度方向的单位矢量，联立式(1)～(3)，得

(4)

由式(4)可知，合加速度矢量等于射流轨迹切向和法向方向加速度的矢量和。将式(4)两端同时乘以射流微元体的质量m可得

(5)

将式(5)向i和j方向投影，并将空气阻力对射流角加速度的影响用系数k表示，则

(6)

以消防水炮射流轨迹的最高点为分界点，可将轨迹分成上升和下降两段。通过分析水射流的实际运动轨迹，发现水射流的速度方向变化率，即角加速度，在上升段和下降段存在明显差异。以k1代表上升段的角加速度修正系数，则上升段消防水炮射流轨迹理论模型微分方程组为

(7)

式中，x为消防水炮水平方向的射程；y为消防水炮垂直方向的射高。

以k2代表下降段的角加速度修正系数，则下降段消防水炮射流轨迹理论模型的微分方程组为

(8)

根据外弹道学原理，将在空气中运动的射流微元体近似为速度低于1马赫的弹丸，所以射流微元体所受空气阻力可表示为[14]

(9)

式中，ρ为空气密度；SM为水射流横截面积；cx为空气阻力系数。

空气阻力一般由摩阻、涡阻和波阻3部分组成。由实践经验可知，当物体飞行速度小于0.6马赫时，激波现象不会产生，即不会产生波阻。所以摩阻和涡阻为消防水炮水射流在运动时所受空气阻力的主要组成部分，在这两种阻力下空气阻力系数cx可用雷诺数表示为

(10)

由消防水炮射流轨迹的特点可知，上升段水平方向的长度大于竖直方向的高度，下降段竖直方向的高度大于水平方向的长度，同时基于上升段和下降段角加速度与过流断面截面积的变化，分别计算其过流断面的截面面积。上升段截面积公式为

SM=A0(1+aln(1+x)),

(11)

式中，A0为喷嘴截面积；a为上升段截面积变化系数。

下降段截面积公式为

SM=A0(1+bln(1+y0-y)),

(12)

式中，y0为射流最高点的射高；b为下降段截面积变化系数。

2 理论模型及算例分析

2.1 理论模型的计算

通过解析法确定方程组(7)和 (8)的解相对困难，因此采用四阶Runge-Kutta算法对方程组进行求解。计算公式为

(13)

式中，K1为计算起点处的斜率；K2为计算时间段中点的斜率，根据欧拉法由K1计算；K3为计算时间段中点的斜率，根据欧拉法由K2计算；K4为计算终点处的斜率；h为时间步长。K1、K2、K3、K4的表达式分别为

采用MATLAB软件对射流轨迹进行仿真，正确选取数值计算的时间步长和时间步数非常重要。步长取值过小会引起计算时间变长，步长取值过大将导致计算精度较低，经过反复试算，确定时间步长取为0.01 s较为合适。

在时间步数的选取上，针对上升段，从水炮安装位置计算至射流轨迹最高点为止；针对下降段，当水落地时y的取值为零，但是由于在给定时间步长直接取到零的可能性不大，因此选取第一个y小于零的值作为下降段的计算终点，再通过最后3个点的二次插值确定射流轨迹与地面交点的坐标。

射流轨迹理论模型中的系数k1、k2、a和b的确定对于射流轨迹预测误差的影响较大，拟通过遗传算法对上述4个系数进行优化，算法流程示意图如图2所示，为避免标准遗传算法易陷入局部最优解的缺点，本文采用多种群并行遗传算法进行计算，将基本遗传算法中的单一种群改为3个并行的子种群，每个子种群按不同的交叉概率和变异概率并行计算，然后将各子种群单独进化S次后的总最优个体分配到所有的子种群中去，其中各子种群的选择算子为轮盘赌选择法，交叉算子为单点交叉，变异算子为基本位变异，各子种群规模均为30。图中射流轨迹的可决系数，亦称拟合优度，是衡量自变量对因变量变动解释程度的指标，即射流轨迹拟合度评价指标，其值越接近于1说明曲线拟合度越好。可决系数计算公式为

(14)

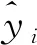
为验证射流轨迹模型的准确程度，以美国Task Force Tips公司两种消防水炮为例，对其射流轨迹进行预测。

2.2 算例分析1

首先对加装YST-4NN型炮头的消防水炮射流轨迹进行预测。该水炮的工作压力689.5 kPa，额定流量94.625 L/s，炮头距离地高度0.61 m，炮口等效直径57.15 mm。则其炮口初速度为

(15)

式中，Q为额定流量；d为炮口等效直径。

各仰角下消防水炮射流轨迹计算所需参数如表1所示。

表1 各仰角下射流轨迹计算所需参数Tab.1 Parameters for jet trajectory calculating at various elevation angles

将上述参数代入射流轨迹模型中，可确定不同仰角条件下消防水炮射流轨迹的预测曲线。由水炮产品手册可确定消防水炮射流轨迹的实际曲线，二者对比如图3所示。

由图3可知，当仰角为30°和60°时，射流轨迹预测值和实测值在各个位置都比较接近，吻合良好，而在仰角为45°和75°的下降段时，二者的误差相对较大，这是由于水射流在下降阶段射流破碎现象加剧，水柱不再是一个相对完整的圆柱体而是逐渐发生破碎，直至最后完全变成无数个小液滴，此时射流微元体所受阻力会变得十分复杂，但理论模型并未很好地考虑这一点。

该型水炮在不同仰角下水射流的射程和射高对比及其误差分别如表2和表3所示。由表2和表3可知，射程和射高的预测值与实际值均非常接近，误差在1%以下，射程最大误差为0.77%，射高最大误差为0.87%。

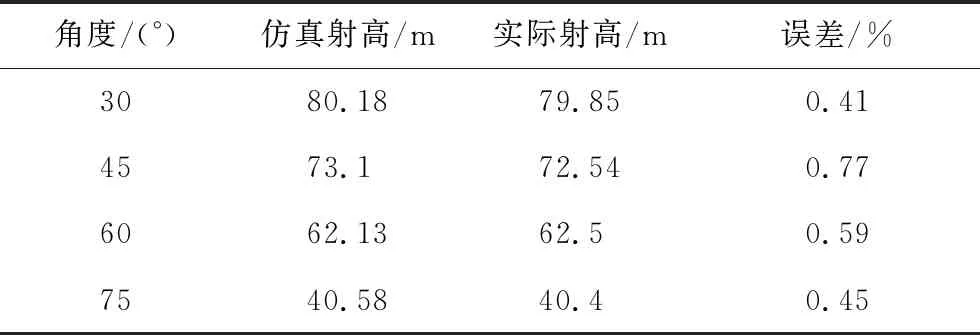
表2 预测射程与实际射程对比Tab.2 The comparison of predicted range and the actual range

在仰角为30°和60°时，射流轨迹预测曲线与实际曲线的拟合优度分别为0.986 9和0.993 2，均与1较为接近，说明两组曲线一致性较高。在仰角为45°和75°时，射流轨迹预测曲线与实际曲线的拟合优度分别为0.966 2和0.919 0，相对来说与1之间有一定的差距，这是由于两组仰角条件下射流轨迹在各自的下降段内同一射程所对应的仿真射高与实际射高有一定偏差，从而造成了拟合优度的计算结果相对偏小，但总体上各仰角下射流轨迹预测曲线与实际曲线的拟合程度较高。

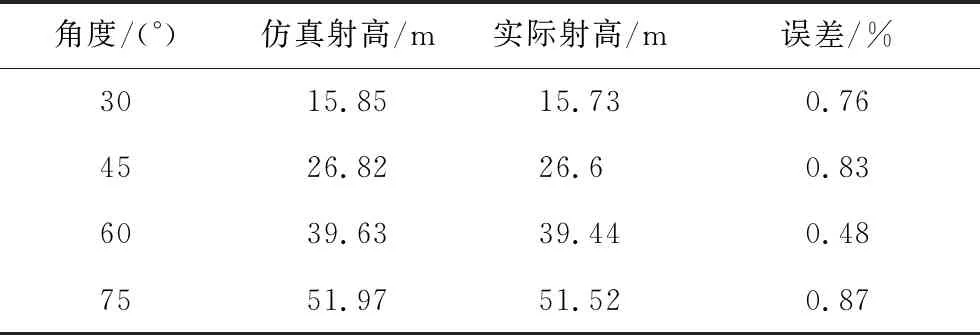
表3 预测射高与实际射高对比Tab.3 The comparison of predicted height and the actual height

2.3 算例分析2

为了进一步验证射流轨迹理论模型的正确性和有效性，拟针对加装MST-4NJ型炮头的消防水炮的射流轨迹进行预测。该消防水炮的工作压力为689.5 kPa，额定流量75.08 L/s，炮头离地高度0 m，出口等效直径50.8 mm。其炮口初速度可根据式(15)计算。

各仰角下消防水炮射流轨迹计算所需参数如表4所示。

表4 各仰角下射流轨迹计算所需参数Tab.4 Parameters for jet trajectory calculating at various elevation angles

该型消防水炮在不同仰角条件下的射流轨迹预测值与实际值如图4所示。由图4可知，当仰角为30°时，射流轨迹预测值和实测值在各个位置都比较接近，吻合良好，而在仰角为45°、60°和75°的下降段时，二者的误差相对较大，同样是由于射流发生明显破碎导致的。

该型水炮在不同仰角下水射流的射程和射高对比及其误差分别如表5和表6所示。由表可知，射程和射高的预测值与实际值均非常接近，误差在1%以下，射程最大误差为0.85%，射高最大误差也为0.85%。

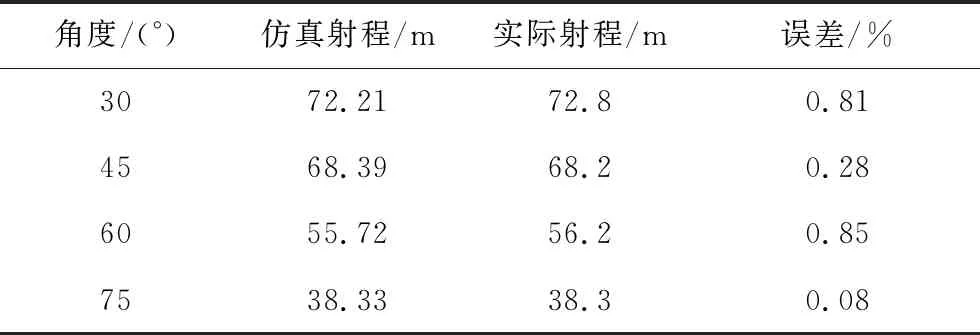
表5 预测射程与实际射程对比Tab.5 The comparison between the predicted range and the actual range

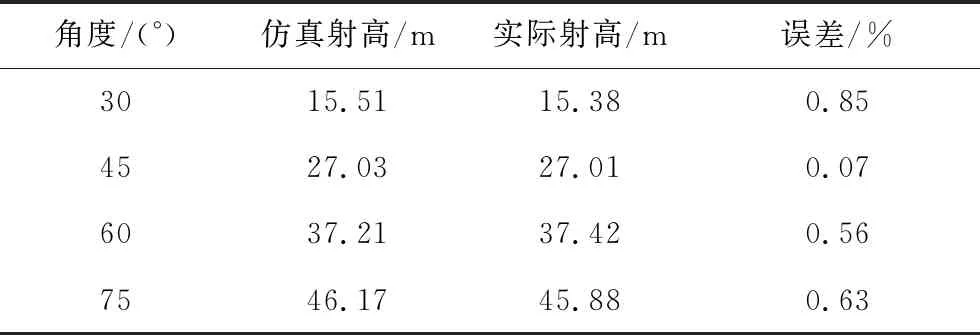
表6 预测射高与实际射高对比Tab.6 The comparison between the predicted height and the actual height

在仰角为30°和60°时，射流轨迹预测曲线与实际曲线的拟合优度分别为0.994 3和0.983 1，均与1较为接近，说明两组曲线一致性较高。在仰角为45°和75°时，射流轨迹预测曲线与实际曲线的拟合优度分别为0.972 6和0.952 8，相对来说与1之间有一定的差距，其原因与仿真算例1类似。

综合以上两个算例中各仰角下射流轨迹的射程、射高和可决系数的计算结果可知，所提出的理论模型能够准确而有效地预测消防水炮射流轨迹。

3 实验验证

为进一步验证消防水炮理论模型的有效性和实用性，利用某大型企业现有消防水炮实验场地进行实验。实验所用水炮如图5所示。

试验用消防水炮的额定流量为80 L/s，炮头距离地的高度为1.5 m，出口等效直径为50 mm。炮口水射流的速度可由式(15)计算得到。

各仰角下消防水炮射流轨迹计算所需参数如表7所示。

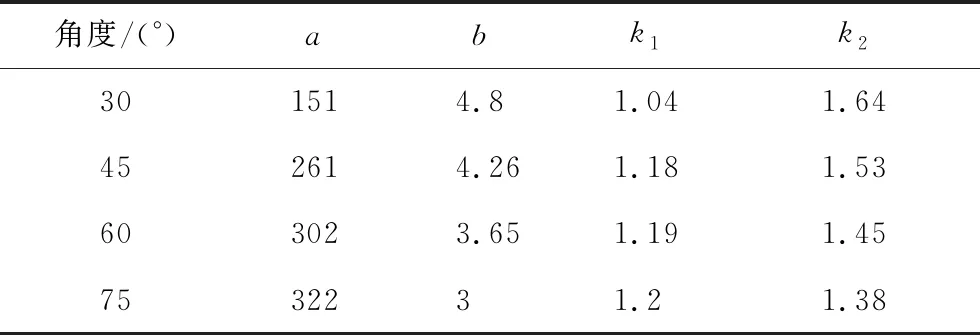
表7 各仰角下射流轨迹计算所需参数Tab.7 Parameters for jet trajectory calculating at various elevation angles

实验过程中水炮射流轨迹如图6所示。

实验过程中，可根据落地点的地面刻度线标记各角度条件下消防水炮的射程。由于实验条件的限制，无法给出消防水炮实际射流轨迹，只能在拍摄消防水炮各仰角条件下的射流轨迹后，根据比例关系计算了消防水炮的射高。所测得的射程实验结果和理论模型预测结果如表8所示。所测得的射高实验结果和理论模型预测结果如表9所示。

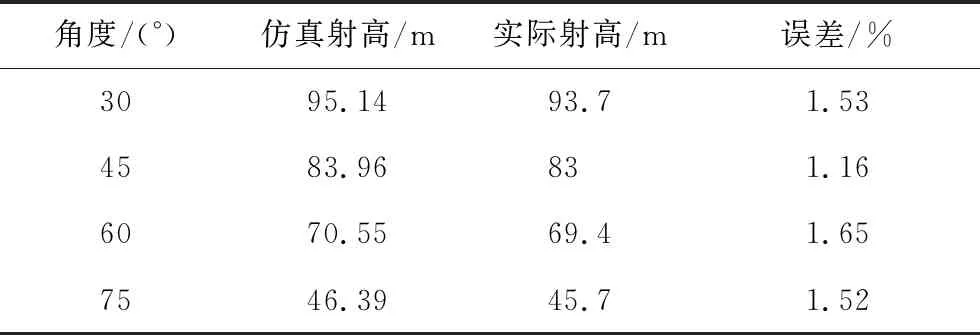
表8 预测射程与实际射程对比Tab.8 The comparison between the predicted range and the experimental range

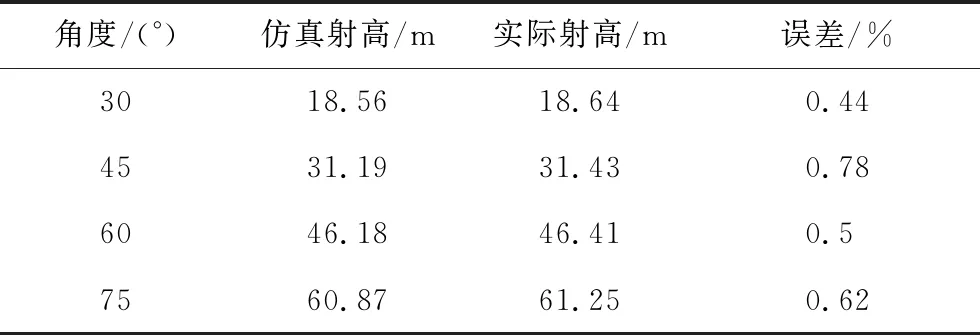
表9 预测射高与实际射高对比Tab.9 The comparison between the predicted height and the experimental height

综上可知，所提出的射流轨迹预测模型与实验的吻合程度较高，射程的最大误差为1.65%，射高的最大误差为0.78%，进一步验证了射流轨迹模型的有效性和实用性。但射程的误差比前述2个算例大，主要是由于实际测量的射流轨迹时存在随机风激励，从而使实验和理论模型的输入条件存在一定的偏差。

4 结论

基于射流破碎对消防水炮射流轨迹上升段和下降段射流形态的影响，引入角加速度修正系数对水射流的力平衡方程进行修正，同时分别以x和y作为自变量描述射流轨迹上升段和下降段的射流截面积变化，建立了一种改进的射流轨迹理论模型。通过对模型算例分析和实验验证，射流轨迹的理论值和真实值吻合良好，受水射流逐渐破碎的影响，射流轨迹下降段的吻合程度低于上升段，各仰角条件下射程与射高的误差均低于2%。所提出的射流轨迹模型可以较为精确地对消防水炮射流轨迹进行预测，从而为消防水炮的智能化提供理论支持。