基于改进的集成经验模态分解法的润滑油磨粒检测研究

苏连成，郭 杰，苏来进

(1.燕山大学 电气工程学院，河北 秦皇岛 066004；2.中国人民解放军61623部队，北京 100842)

0 引言

机械系统在运行过程中有时会因为磨损等问题出现故障，处理这类故障问题的传统方法是定期地关闭和检查系统，然而，对于一些复杂的设备，停机成本会很高，拆卸设备进行诊断可能是不切实际的。对于这些情况，最好使用监控系统来跟踪系统的状态，只有在检测到一些报警信号时，系统才会关闭。所以如何选取一些能够反映机械运行状况的监测指标对机械进行有效的监测变得尤为重要。

机械设备的部件在发生磨损时，会产生一些磨粒，这些磨粒的浓度、尺寸、形态等特征能够反映出机器的磨损形态与程度[1]。所以通过对磨粒的监测能够有效反映出机器的磨损程度，判断出机械的运行状况，以便做出有效的故障预警，为改善机器的工作状况以及设计改进提供重要的依据[2-4]。

而通过传感器采集磨粒信息时，油液磨粒信号传感器由于受到振动以及相应的电路的干扰，导致采集到的信号是掺杂了噪声的调制信号。因此，对于磨粒检测的关键就是如何有效地去除噪声，提取出有效信号[5]。以下是对油液磨粒传感器输出信号进行处理的几种常见方法。

傅里叶变换[6]是建立在理想模型上面的，即假设输入信号是稳定的、线性的：

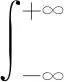
(1)

它的思路是：对于输入信号x(t)，通过式(1)将其从时域转化到频域中去，在频域中对信号进行分析。但是傅里叶变换是针对平稳、线性信号的信号处理方法，所以它无法描述非平稳、非线性信号，而且从公式可以看出，它是对信号整体的变换，无法描述信号的局部信息。

Dennis Gabor等人提出的Gabor变换[7]，将窗口函数的概念引入到傅里叶变换中，然后将其发展成了短时傅里叶变换。短时傅里叶变换广泛应用于非平稳信号分析，它的基本思路是将信号划分为小的时间间隔(窗口)，然后采用傅里叶变换分别得到每个窗口的频率信息，所有窗口的总频率信息将显示信号频率随时间的变化。

通过引入窗口函数g(t)，并不断将窗口沿着信号滑动，可以得到信号x(t)的短时傅里叶变换:

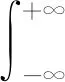
(2)

因为STFT仍然需要对每个窗口中的信号进行傅里叶变换来分析，所以它必须假设每个窗口中的信号是平稳的，这是很难保证的。另外STFT中的时间窗口在处理过程中是不能改变其大小的。所以它无法精确描述频率会随时间变化的非平稳信号。另外如果想要得到较高的时间分辨率，时间窗口就要足够，而如果想要得到高频率分辨率却需要足够大的时间窗，这就意味着STFT无法做到时间分辨率与频率分辨率两者兼得。虽然STFT有一些缺点，但它的优点是很容易实现的。

基于小波变换的方法[8]继承和发展了STFT的思想，同时又克服了窗口大小不随频率变化等缺点，它的主要思路是将信号进行小波分解，然后设定各层阈值，将各层系数按阈值筛选处理之后再重构，得到有效信号，不过小波变换存在小波基以及各层阈值的选取问题[9]。

经验模态分解法(Empirical Mode Decomposition,EMD)[10]是基于信号的自适应的信号分解法，它可以将复杂信号按照频率分解成多个固有模态函数以及一个残余量，有助于提取信号的性质及其基本的物理特性[11]。然而，EMD也有明显的不足之处[12-14]。

针对EMD的不足，本文改进了EMD方法，在EMD处理过程中引入了噪声辅助数据分析(Noise Assisted Data Analysis, NADA)方法来克服信号间歇性带来的弊端。并且提出了其超参数的自适应设定方法。改进后的方法虽然减轻了EMD的一些缺点，但由于结果是集成平均得到的，也给分解结果带来了一些副作用。本文分析了其不良反应，并采用了后期处理的方法，取得了较好的效果。

之后本文建立起传感器输出电动势的模型，然后通过模型分析出了磨粒尺寸特征(磨粒磁性、尺寸、数量等)与输出电信号幅频特性(包括峰峰值、相位等)的关系，通过计算、统计电信号的相关信息，拟合出了磨粒尺寸(半径)与输出电动势波峰值、波谷值以及峰峰值的模型曲线，并验证了模型的准确性。最后通过对输出信号的处理，从中提取出了磨粒尺寸、数量、磁性等信息，为后续机械磨损状况的研究，故障分析诊断打下了基础。

1 经验模态分解方法

1.1 经验模态分解法的步骤

EMD能够将复杂的非平稳信号分解为有限的具有物理意义的固有模态函数(Inherent Modal Function, IMF)以及残余分量，这样可以有效地将磨粒信号与噪声干扰分离开来，分析相应的IMF就可以准确地提取出磨粒信号的特征信息[15]。

一般来讲，现实世界中的信号都是由一些IMFs叠加而来的。而任何一个IMF都满足以下两个条件：

1) 在整个数据信号中，极值点(包括极大值以及极小值)的数量和过零点的数量相等或者只差一个；

2) 在任何一个时间点上,极大值点的上包络线的平均值与极小值点的下包络线的平均值之和为零，也就是信号关于X轴局部对称。

EMD方法的分解步骤如图1所示(设原始信号为x(t))。

最后，原始信号被EMD方法分解成了几个固有模态函数与残余量之和。

1.2 经验模态分解法的不足

对EMD算法精度影响最大的是模态混叠问题。模态混叠是由信号的间歇性(信号间歇是一种无固定形式并且无法确定何时出现的干扰信号)所引起的。它会导致不同的IMF之间相互混叠，各自包含对方的成分，使得最后无法有效地将固有模态函数分离出来。

端点效应是EMD算法出现的另一个问题，端点效应会使分解出的信号端点处出现失真现象，发生较大的畸形波。端点效应的出现一方面会导致当前分解得到的信号失真，另一方面也会影响到接下来的信号分解，导致下面的分解错误。

2 改进的带后期处理的集成经验模态分解法

2.1 改进的集成经验模态分解法的步骤

本文针对EMD存在的问题，提出了改进的带后期处理的集成经验模态分解法(Improved Integrated Empirical Modal Decomposition Method, IIEMD)方法，它能够有效解决信号间歇问题。大体思路是通过在EMD分解过程中引入白噪声来抑制信号的间歇性，而由于白噪声具有零均值的特点，所以可以采用多组分解之后再求平均的方式来消除引入的白噪声。IIEMD不仅能够显著地缓解模态混合问题，而且减少了端点效应等的影响。IIEMD具体步骤流程图如图2所示(为集成组数)。

但是由于最后IIEMD分解的结果是由多组计算求平均得到的，得到的分解结果有可能不符合固有模态函数的特性，因此，本文对IIEMD方法加入了后期处理，保证其最后的结果满足固有模态函数的要求，以便于之后对信号的处理。后期处理的基本思想非常简单，因为IIEMD的结果不符合固有模态函数的严格定义，所以可以把它们当作原始信号用EMD方法处理。经过原有的EMD方法处理后，得到的新的固有模态函数就会更加地符合固有模态函数的定义。对于处理的细节，考虑到信号的完整性，每个固有模态函数都需要一个EMD过程。后期处理过程流程图如图3所示(设IIEMD法分解所得固有模态函数数量为n)。

2.2 白噪声幅值以及集成数等超参数的自适应化

与EMD相比，IIEMD不再是自适应的方法，它在引进白噪声的同时，两个需要人为设定的超参数也随之而来：白噪声的幅值以及集成组数N。

对于白噪声的幅值，需要设置一个适当的值，当原始数据以高频信号为主时，需要一个较小的噪声幅值，如果原始数据以低频信号为主，需要一个较大的噪声幅值。由于在原始信号中引入白噪声是为了处理间歇性，如果能够估计间歇性的幅值，也可以作为设置噪声幅值的参考。

需要注意的是，而在分解过程中如果增加噪声幅值，将需要更多的集成操作来减少白噪声的影响。集成数量决定了在分解过程中将执行多少集成操作。在每个集成操作中，IIEMD都会向原始数据添加一系列白噪声，并执行EMD分解。增加集成组数的数量就需要更多的计算时间，会大大降低IIEMD的效率。

所以为了降低附加噪声的影响，首先应该考虑降低白噪声的幅值，而不是增加集成数。然而，这些规律只能缩小设定范围，却没有公式可以帮助正确选择白噪声的幅值，对于白噪声的幅值，还是只能通过具体的实验数据尝试验证。

所以经过试验，本文提出了应用于IIEMD法的自适应设定白噪声幅值参数的方法：

(3)

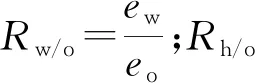
(4)

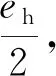
对于集成数的参数问题，Wu Z H等[16-17]提出了加入白噪声的幅值标准差与集成数之间的关系为

(5)

式中，ed是期望的信号分解相对误差最大值，N为集成数，所以，在确定了加入的白噪声的幅值标准差以及期望的信号分解相对误差最大值之后，N也可以唯一确定。

图4(a)所示为一个正弦信号，对其加入间歇性噪声后如图4(b)，然后分别采用EMD以及改进的IIEMD对其进行分解，具体结果如图5、6所示。由图5可知，当加入有间歇性的噪声之后，采用EMD的分解结果存在明显的模态混叠问题，信号无法有效地分解出来。而从图6所示的改进的IIEMD分解的结果可以看到，信号已经被准确分解出来，IMF4即为最初的未加噪声的正弦信号，而加入的间歇信号被分解在IMF1中，可见改进的加入后期处理的IIEMD法可以有效地抑制模态混叠问题，提高信号分解的准确性。

图7为一个真实的单个磨粒通过传感器的输出信号，通过采用改进的IIEMD法将其分解，分解结果如图8～11所示，可以快速从中找到单个磨粒通过所产生的类正弦信号IMF6，有效地提取出有用信号。

3 油液磨粒输出信号模型

由上文可知，磨粒信号已经能够被有效地分离出来，下面要做的就是如何从有效信号中提取出磨粒的相关特征。本文采用的油液传感器是三线圈双激励电感式传感器，示意图如图12。

分析其激励线圈产生的磁场，以磨粒P所在圆面为XOY平面，轴心为原点，轴向为Z轴建立坐标系，采用极坐标的表示方法，则磨粒P的坐标为(p,φ,Z)，设激励线圈单位电流的坐标为Q(p′,φ′,Z′)，首先，先计算单个激励线圈所产生的磁场：

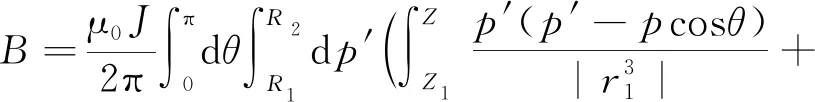
(6)

其中，

n为感应线圈匝数，R1为激励线圈内径，R2为激励线圈外径，Z1、Z2为激励线圈前后端的轴向坐标，μ0为电磁常数。

则轴线上的磁场强度为

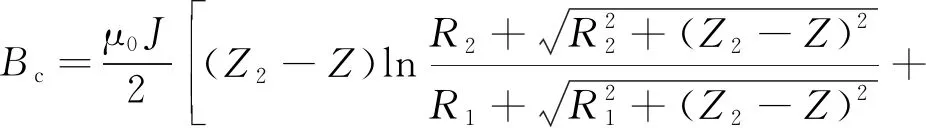
(7)

令

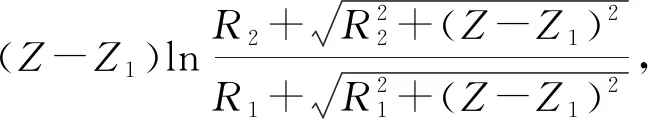
则两个激励线圈形成的磁场为

(8)

Z1、Z2、Z3、Z4分别为两个激励线圈前后端的轴向坐标。

当磨粒进入磁场时，因为磨粒磁导率的不同，它本身体积内的磁场发生变化，导致整个磁场的磁通量发生改变：

Δφ=ΔBS=(μf-1)πr2BallVd,

(9)

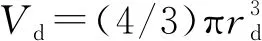
(10)

令激励电源频率为f，线圈激励为i=Isin(2πft)，则

(11)

N为初级线圈匝数,若磨粒为匀速运动，运动速度为ν，则Z=νt，感应电动势为

(12)

其中，因为频率的值远大于速度，所以括号里的后半部分对电动势的影响很小，忽略这一部分：

(13)

则由磨粒产生的(去掉交流激励电源)感应电动势表达式为

(14)

由上式可知，当确定传感器的各项尺寸参数以及交流激励电源和磨粒的速度之后，输出电动势与磨粒半径的三次方成正比。

4 从输出信号提取磨粒尺寸特征

如上文所述，模型已经建立，通过分析输出信号幅频特性就能够提取出磨粒的特征信息。

磨粒的数量信息通过输出信号的极值个数来计算，由于单个磨粒的输出是一个类正弦波的信号，所以输出信号的极值的个数就是磨粒的个数。

而通过输出信号的相位可以判断出磨粒的磁性特征，这是因为铁磁性磨粒的磁导率是大于1的，而非铁磁性磨粒的磁导率小于1，当铁磁性磨粒(非铁磁性磨粒)进入传感器磁场时，对磁场起增强(削弱)的作用，导致产生的感应电动势是先正后负(先负后正)的，所以可以通过输出信号的相位，判断出磨粒是铁磁性磨粒还是非铁磁性磨粒。

磨粒的尺寸信息可以通过上文得到了磨粒尺寸信息与输出的感应电动势之间的关系计算得到。实验采集样例，拟合出相应的输出曲线，通过相对应的输出信号的波峰值、波谷值以及峰峰值(波峰值与波谷值之差)可以求得磨粒的半径尺寸。

本文实验首先通过显微镜测量出一组具有尺寸梯度的磨粒的半径，测量实例示例如图13所示，然后依据上文提出的改进的IIEMD方法提取出了去除了噪声干扰的输出信号，测得了其对应的波峰值、波谷值以及峰峰值的具体数值。具体数据如表1所示，之后拟合出了波峰值、波谷值以及峰峰值对应于磨粒半径的模型曲线。采用同样的方法测得了与表1所示磨粒尺寸不同的磨粒，计算出相对应的波峰值等信息，如表2所示，用来验证拟合曲线的准确性。

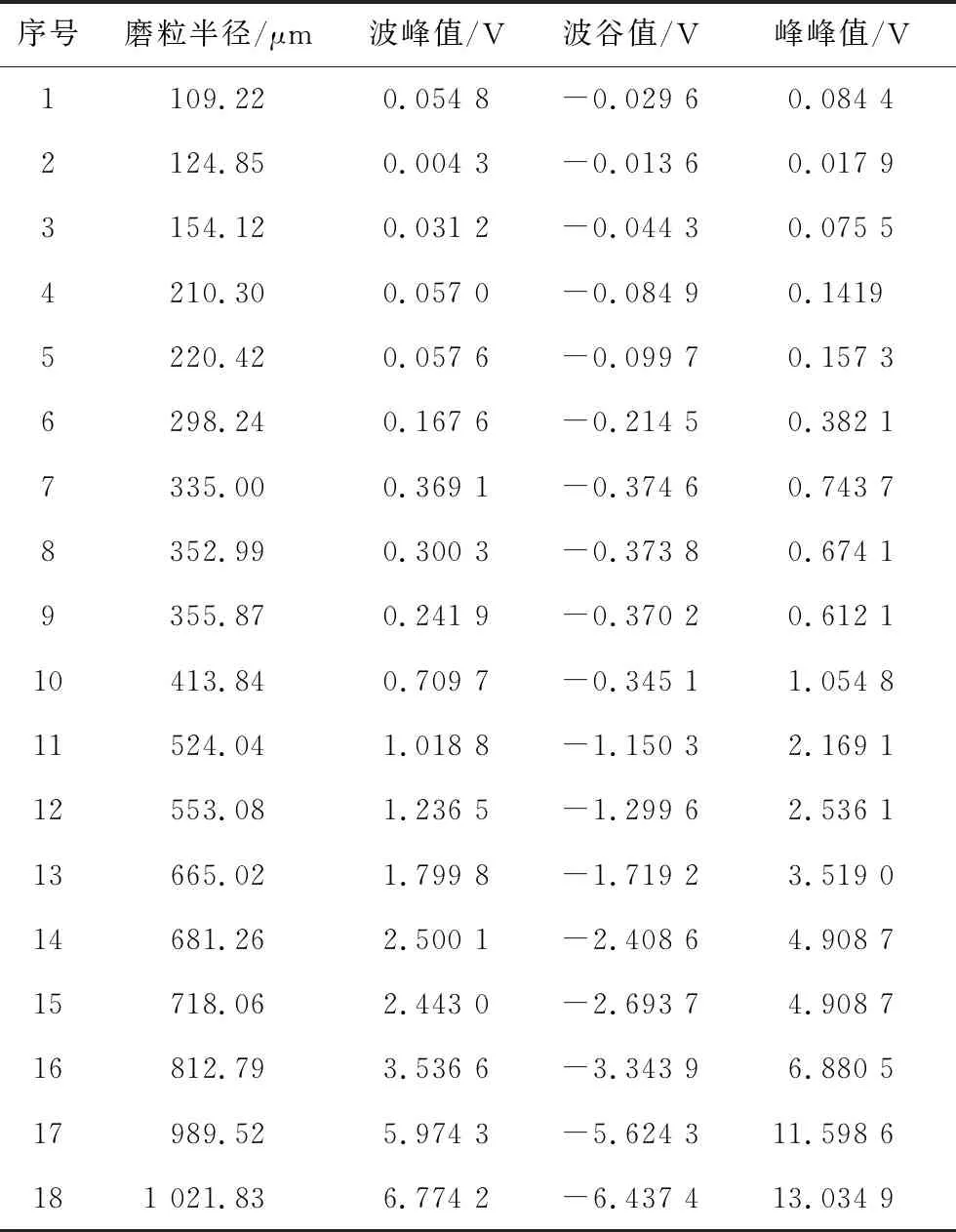
表1 实验磨粒信号输出峰值Tab.1 Experimental particle signal output peak

采用表1样例数据拟合所得的磨粒半径尺寸与输出信号的波峰值、波谷值以及峰峰值的具体表达式为

Epeak=4.368 3×10-9d3+2.373 0×10-6d2-
4.938 5×10-4d+0.031 4，

(15)

Etrough=-2.734 7×10-9d3-4.185 5×10-6d2+
0.001 1d-0.090 2，

(16)

Epeak-trough=7.103 0×10-9d3+6.558 5×10-6d2-
0.001 6d+0.121 7。

(17)

采用表1与表2样例数据拟合的曲线如图所示，图14、15、16分别为波峰值、波谷值以及峰峰值对应磨粒半径的拟合曲线，其中星号所示数据为表1用来拟合曲线的样例，三角形所示数据为表2用来验证拟合曲线准确性的样例。图17、18、19为相应波峰值、波谷值以及峰峰值的拟合曲线残差数据图，星号所示数据为拟合曲线的样例，三角形所示数据为验证拟合曲线准确性的样例。

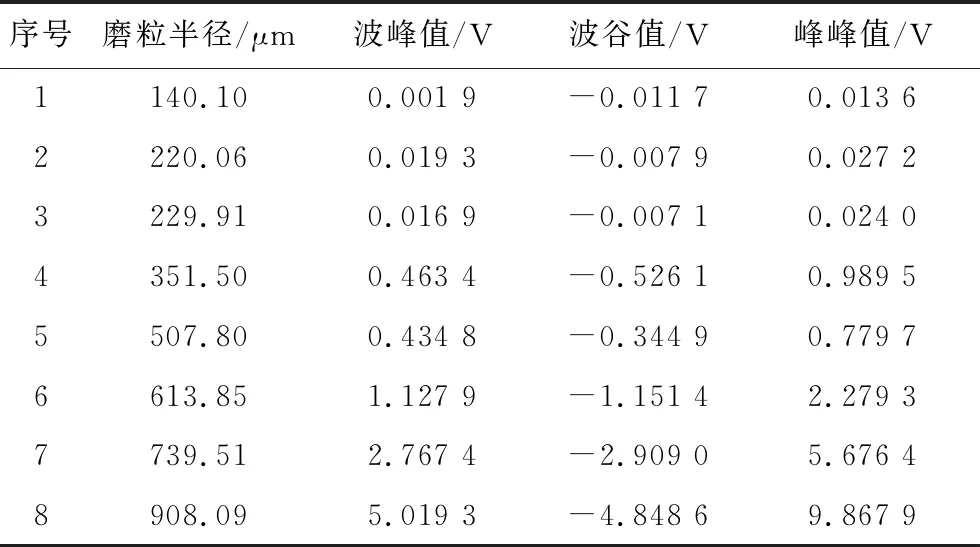
表2 磨粒信号输出峰值Tab.2 Particle signal output peak

由图可以看出无论波峰值、波谷值还是峰峰值曲线拟合的都比较好，验证数据的误差也不大，绝大多数数据残差都聚集在X轴附近，基本可以体现出磨粒的尺寸特性，较好地验证了曲线的准确性，几个误差相对较大的点如半径尺寸为507.80 μm、613.85 μm等磨粒，主要原因在于这些磨粒的形状比较细长，因此所测的最小外径圆，与它们本身面积相比过大，所以导致了较大的误差，但考虑到形状很不规则的磨粒大多出现在尺寸较大的区域，所以相对误差也不是很大。而且，后期可以对磨粒尺寸进行分段研究来减小误差。相比较而言，波峰值与磨粒半径尺寸的拟合曲线的误差最小，而峰峰值可以加大输出信号的值，有利于小尺度范围的测量。实验表明了输出信号的极值特性与磨粒尺寸的关系，验证了模型的准确性。

5 结论

改进的IIEMD方法通过对原始信号引入白噪声克服了因信号间歇性导致的模态混叠与信号失真问题，提高了信号提取的准确性与稳定性，同时对于白噪声的幅值选取以及集成数等超参数提出了设定方法，保证了IIEMD的自适应性。而且通过引入后期处理，提取出的有用信号更加满足IMF的特性，便于后面信号的特征提取，提高了拟合模型的精度。

对于磨粒特征信息的提取研究，通过对输出信号的处理，拟合了磨粒尺寸与输出信号的模型，并验证了模型以及曲线的准确性，从中提取出了磨粒尺寸、数量、磁性等信息，为后续机械磨损状况的研究，故障分析诊断打下了基础。