基于交织法构造最优时频二维低碰撞区跳频序列
2020-10-23许成谦
许成谦,边 强
(燕山大学 信息科学与工程学院,河北 秦皇岛 066004)
0 引言
由于通信业务用户量的不断增多,对多址技术的研究就显得尤为重要。跳频序列用于区分跳频码分多址通信系统中的用户,可以使多个用户共享同一频带,提高频带利用率,同时,系统中也存在着多址干扰影响系统容量[1]。因此,通过构造最优跳频序列集将多址干扰降到最小成为研究重点[2-3]。跳频序列的性能受频隙的多少、序列长度、序列数目和最大汉明相关值的影响[4],因此,跳频序列在设计的过程中,需要在满足理论界的情况下,汉明相关值尽可能小,用到的频隙尽可能多等。目前为止,国内外学者已经构造出了许多一维最优的跳频序列集,而随着跳频通信系统的信号传输速度不断提高,不仅要考虑时间延迟,还要考虑多普勒频移。因此,构造关于理论界最优的时频二维低碰撞区跳频序列集来增强跳频通信系统的抵抗干扰的性能有着重要意义。
近些年,在跳频序列的理论界方面和跳频序列的构造方面的研究成果显著。文献[5]给出了跳频序列集关于平均汉明相关函数的理论下界。文献[6]给出了两类跳频序列集关于平均周期汉明相关函数的理论界,并分别给出了改进版。文献[7]对Peng-Fan-Lee界进行了进一步推广,研究了时频二维低碰撞区跳频序列集最大周期汉明相关性能,并推导了理论界。文献[8]提出了一种基于交织法构造最优低/零碰撞区跳频序列集的方法,且相关区的长度在满足一定条件下可灵活选取。文献[9]基于交织法构造出了几类具有最优周期汉明相关性质的跳频序列集。文献[10]利用交织技术和新构造的一类移位序列得到了一类关于平均周期汉明相关性质的研究最优的跳频序列集。文献[11]基于交织技术给出了一般跳频序列集的构造方法并构造出了一类最优的跳频序列集,最后给出了一类特殊的移位不等价序列的构造方法。文献[12]基于交织技术构造出了一类最优的跳频序列集。文献[13]利用交织技术构造了一类最优周期汉明相关低碰撞区跳频序列集,并消除了序列的等价移位性。文献[14]分析了两类时频二维分圆跳频序列的汉明相关性,并给出了满足最优的条件。
文献[15]基于Welch Costas 阵列和Golomb Costas阵列得到的两类最优时频二维低碰撞区跳频序列集,本文首先将利用基于Welch Costas 阵列构造的最优时频二维低碰撞区跳频序列集与两类移位序列分别进行交织得到的跳频序列集并成一个跳频序列集。然后,本文又将基于Golomb Costas阵列构造的最优时频二维低碰撞区跳频序列集与两类移位序列分别进行交织得到的跳频序列集并成一个跳频序列集。新得到的两类时频二维低碰撞区跳频序列集的序列数量更多、序列长度更长,抗干扰性能更好。
1 基本概念
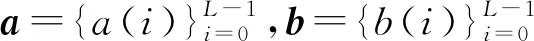
认知弹性超文本是由节点与表达节点之间的链组成的网状结构,其典型特征是具有概念功能的搜索能力,达到知识扩充的效果,同时,其内容还可以被重新编辑,以产生一种特殊的概念纵横交错的知识结构。但研究表明,认知弹性超文本并不适宜一切教学情境,仅适用于需要进行高级知识获得学习的结构不良领域。在这一类型中,学习者必须达到两个基本目标:掌握概念的复杂性;具备将已有知识独立运用至新情境的能力。
(1)
综上所述,序列集B是一个参数为(t(p-1),W[m-(n-1)t+n-1],p-1,s-1,p-2,t)的TF-LHZ跳频序列集。
今年是化肥销售市场最困难的一年,化肥销量首次下降,化肥销售没有旺季,生意很不好做。由于化肥价格波动较大、需求量减少,农资企业今年的化肥销售量普遍下降。预计接下来的化肥市场依然以稳为主,化肥企业应把握市场行情、加快转型升级,不断适应农资和农业行业供给侧改革的新形势。
(2)
τ表示时延,ω表示频移,且0≤τ≤L-1,ω∈F,i+τ≡(i+τ)modL。当a=b时,Ha,b(τ,ω)称为二维周期汉明自相关函数;当a≠b时,Ha,b(τ,ω)称为二维周期汉明互相关函数。
定义2设A={a0,a1,…,aM-1}是F上M个长度为L的跳频序列组成的集合,令整数
3)从系统工程角度来看,以降低泵压作为节能的直接手段,面向单井、管线与注配间,综合应用地面工程、采油工程和油藏工程的措施开展综合性节能降耗工作,对注水系统节能降耗有一定的指导意义。
Ha(A)≥0,Hc(A)≥0,
k,j=0,1,…,M-1,
定义:
LAt=max{T|Hak,ak(τ,ω)≤Ha(A),∀ak∈A,0≤τ≤T,0≤ω≤V,(τ,ω)≠(0,0)},
LAf=max{V|Hak,ak(τ,ω)≤Ha(A),∀ak∈A,0≤τ≤T,0≤ω≤V,(τ,ω)≠(0,0)},
LCt=max{T|Hak,aj(τ,ω)≤Hc(A),∀ak,aj∈A,0≤τ≤T,0≤ω≤V,k≠j},
LCf=max{V|Hak,aj(τ,ω)≤Hc(A),∀ak,aj∈A,0≤τ≤T,0≤ω≤V,k≠j},
Lt=min{LAt,LCt},Lf=min{LAf,LCf}
若(Lt,Lf)≠(0,0),则[0,LAt]×[0,LAf]称为A的时频二维周期自相关低碰撞区,[0,LCt]×[0,LCf]称为A的时频二维周期互相关低碰撞区,[0,Lt]×[0,Lf]称为A的时频二维周期低碰撞区,称A是(L,M,q,Lt,Lf,Ha(A),Hc(A))时频二维周期低碰撞区跳频序列集,简称为TF-LHZ跳频序列集。
2.2 两组新生儿指标比较 观察组新生儿出生体质量、巨大儿4例(5.00%),对照组分别为(3.81±0.73)kg和15例(18.75%),差异有统计学意义(t=-8.33,P=0.02;χ2=21.60,P=0.00);两组新生儿窒息率均为2.50%(2/80),差异无统计学意义(χ2=1.31,P=1.24)。
当Ha(A)=Hc(A)=0时,称序列集A的时频二维低碰撞区为序列集A的时频二维无碰撞区。当(Lt,Lf)≠(0,0)时,称序列集A为时频二维周期无碰撞区跳频序列集,简称为TF-NHZ跳频序列集。
引理1[7]设频隙集合F是q阶加法群,序列集A是由F上M个长度为L的跳频序列组成,[0,Lt]×[0,Lf]是A的时频二维低碰撞区,最大周期汉明自相关为Ha(A),最大周期汉明互相关为Hc(A),对于任意正整数Z1和Z2,(0≤Z1≤Lt,0≤Z2≤Lf),Hm=max{Ha(A),Hc(A)},则
(3)
当取得等号时,序列集A是最优TF-LHZ跳频序列集。
2 交织法理论
交织法理论由Gong在1995年首次提出[16],2002年,Gong又将该理论进一步完善[17]。
构造方法Ⅰ:

Le(j)(aj)=(aj(0+e(j)),aj(1+e(j)),…,
aj(L-1+e(j))),
则交织序列可以表示为
x=I(Le(0)(a0),Le(1)(a1),…,Le(M-1)(aM-1)),
其中,I表示交织操作。
然而,依托PSCAD仿真软件对10 kV线路进行潜供电流计算发现,在典型参数下,5 km同杆并架10 kV线路出现两相或三相短路时,故障线路上潜供电流不到3 A,感应电压不超过300 V,难以形成稳定的弧道,不会对故障点熄弧产生影响。
y=I(Lg(0)(a0),Lg(1)(a1),…,Lg(M-1)(aM-1))。
引理2交织序列x和y的时频二维周期汉明相关函数有如下性质:
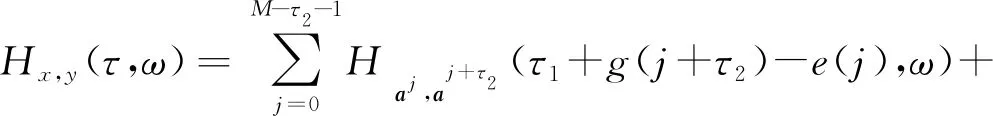
(4)
序列集B的时频二维汉明自相关函数和汉明互相关函数分别为
Lτ(y)+ω=I(Lτ1+g(τ2)(aτ2+ω),…,
Lτ1+g(M-1)(aM-1+ω),Lτ1+g(0)+1(a0+ω),…,Lτ1+g(τ2-1)+1(aτ2-1+ω)),
则
推论1若
同理可得,当(τ,ω)∈[0,s-1]×[0,p-2]时,有
(5)
3 基于交织法构造TF-LHZ跳频序列集
所有超声造影与增强CT造影全过程均用同步录像并存盘,最后将图像全程回放,由2名有经验的影像科医师进行分析并作出诊断。
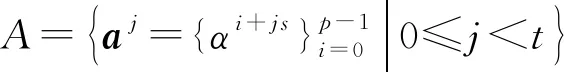
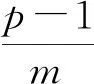
其中,el(i)=(l+ni)m+ni,gk(i)=(l+c)m+c,nt-n

xi=I(Lel(0)(aj),Lel(1)(aj),…,Lel(t-1)(aj)),
i=jW+l(0≤j yi=I(Lgk(0)(a0),Lgk(1)(a1),…,Lgk(t-1)(at-1))。 3)将得到的跳频序列集X和Y并成一个新的跳频序列集B,即B=X∪Y。 定理1序列集B是一个参数为(t(p-1),W[m-(n-1)t+n-1],p-1,s-1,p-2,t)的TF-LHZ跳频序列集。 海底通信光缆包括独立海底光缆和海底光纤复合电缆(即光电复合缆)两个类型。近年来,光电复合缆使用较为广泛,其暴露的问题也相对较多。光电复合缆将电能输送和信号传输与整合于一体,充分利用光纤传输信号不受电磁场干扰的特点,将若干光纤单元放置于电缆电力芯间的空隙中,传输信息,实现通信联络和远端控制[3]。 证明: 由文献[15]可以得到,序列集A是一个序列的长度为p-1、序列的数目为t、频隙大小为p-1、时频二维低碰撞区为[0,s-1]×[0,p-2]、最大汉明相关值为1的最优TF-LHZ跳频序列集。依照交织技术理论,可以得出序列集B中的序列长度为t(p-1),频隙大小为p-1,序列集中的序列个数为M=W[m-(n-1)t+n-1]。 取时延τ=tτ1+τ2,0≤τ1 Lτ(yr)+ω=I(Lgk(τ2)(aτ2(i+τ1)+ω),Lgk(τ2+1)(aτ2+1(i+τ1)+ω),…,Lgk(t-1)(at-1(i+τ1)+ω),Lgk(0)+1(a0(i+τ1)+ω),Lgk(1)+1(a1(i+τ1)+ω),…,Lgk(τ2-1)+1(aτ2-1(i+τ1)+ω)), 则根据引理2可得 其中,0≤l 则根据推论1可得 第三,擅长挖掘自身的亮点和资源。一个18岁的少年,没有工作经验,大学只上了一个学期,看上去毫无亮点,但乔布斯很聪明,他自信地捕捉到了自己身上的闪光点和独特的资源,并且写了出来。比如,他在地址一栏填的是“里德学院”。里德学院在美国是响当当的名校,专注学术,博士毕业比例占据全美第三,也是美国第一所拒绝U.S.News大学排名的学校,以个性、奇才而闻名,里面的学生也是如此。乔布斯把自己的地址定在“里德学院”,其实是委婉地自我加分,说明自己也是一个奇才,虽然他因为经济原因早早辍学了。 因为跳频序列集A是参数为(p-1,t,p-1,s-1,p-2,1)的最优TF-LHZ跳频序列集,所以在(τ,ω)∈[0,s-1]×[0,p-2]时,有Hm(A)≤1,因此可得 “我就给他家人出了个主意,七个子女谁养老太太,商铺就归谁,老太太养老送终全托给他。其他子女有心意的去尽点心意,没有心意的也不强求。”李敬益估算了下,依据市值这商铺值5万,都归抚养者,有理有据,大家也许能接受,接下来就得逐个攻破。 Haj,aj+τ2(τ1+dj,τ2,ω)≤1, 所以,当(τ,ω)∈[0,s-1]×[0,p-2]时,Hxi,yr(τ,ω)≤t,即Hm(B)=t。 且dj,τ2要进行模L运算,则 Hxi0,xi1(τ,ω)≤t 其中, 定理2序列集的B是最优TF-LHZ跳频序列集。 证明: 智和智拓营销咨询公司总经理颜东从宏观、原材料等多方面对肥料行业近期及未来发展进行了分析。据他介绍,尿素后势企稳,或有阶段性上涨;磷铵涨势已起;钾肥需结合国际大合同结果,呈上涨趋势。他表示,整体而言,化肥行业持续推进供给侧改革,安全、环保持续高压,能源和原料市场高位运行,复合肥的成本压力因此在不断扩大,拥有原料和品质优势的生产企业将会形成明显的竞争优势。 令L=t(p-1),M=W[m-(n-1)t+n-1],q=p-1,Z1=s-1,Z2=p-2,Hm(B)=t。由 根据引理1可得,序列集B是最优TF-LHZ跳频序列集。 a0=(1,3,2,6,4,5),a1=(6,4,5,1,3,2)。 2)令W=1,m=6,n=2,构造移位序列集H={E,G},有 3)利用以上构造方法可得到参数为(12,5,6,2,5,2)的最优TF-LHZ跳频序列集B={b0,b1,b2,b3,b4}, b0=(1,2,3,6,2,4,6,5,4,1,5,3),b1=(6,5,4,1,5,3,1,2,3,6,2,4),b2=(6,1,4,3,5,2,1,6,3,4,2,5),b3=(4,3,5,2,1,6,3,4,2,5,6,1),b4=(5,2,1,6,3,4,2,5,6,1,4,3)。 证明:对于时延τ=Mτ1+τ2,0≤τ1 由此可见,在碰撞区[0,2]×[0,5]上,Hb0,b0(τ,ω)≤2((τ,ω)≠(0,0)),Hb0,b1(τ,ω)≤2,所以,Hm(B)=2,满足定理1和定理2,因此,跳频序列集B是一个参数为(12,5,6,2,5,2)的最优TF-LHZ跳频序列集。 构造方法Ⅱ: 利用手机微信进行微课程学习,通讯网络费用是绕不开的话题。为了花最少的钱学习更多的课程,微信微课程在设计时应该进行资源合理整合,文字、图片和视频组合在一起,同时提供可下载的资源,达到减少移动通讯费用的目的。 步骤2:与构造方法Ⅰ的步骤2相同。 内部行政的有序性是现代企业生产运营的前提,同样也是企业在大数据环境和技术支持下对电子供应链金融风险管理的核心策略。通过实际调查发现,我国许多中小型企业对于企业内部电子供应链金融管理工作无法做出有效判断和行政管理。对此,首先需要完善内部风险行政管理体制,加强企业部门行政规划,保证部门工作的充分性和有序性,从而提高抵抗电子供应链金融风险的能力,给领导者提供有力的思想依据。此外,各行政部门的领导者需要及时转变自身观念,不要过分夸大或忽视金融风险的危害,推动企业行政规划更好更快发展。 步骤3:与构造方法Ⅰ的步骤3相同,将得到跳频序列集X和Y并成一个新的跳频序列集B,即B=X∪Y。 定理3序列集B是一个参数为(t(p-1),W[m-(n-1)t+n-1],p-1,s-1,p-2,t)的最优TF-LHZ跳频序列集。 证明:由文献[15]可知,序列集A是一个序列长度为p-1、序列数目为t、频隙大小为p-1、时频二维低碰撞区为[0,s-1]×[0,p-2]、最大汉明相关值为1的最优TF-LHZ跳频序列集,与定理1和定理2的证明同理,可以得到跳频序列集B是一个参数为(t(p-1),W[m-(n-1)t+n-1],p-1,s-1,p-2,t)的最优TF-LHZ跳频序列集。 a0=(∞,2,4,5,3,0),a1=(0,4,1,∞,3,5)。 2)令W=1,m=5,n=2,构造移位序列集H={E,G},有 E=[e0(0),e0(1)]=[0,10],G=[g0(0),g0(1)]=[15,15]。 3) 利用以上构造方法可得到参数为(12,3,6,2,5,2)的最优TF-LHZ跳频序列集B={b0,b1,b2}, 在具体施工过程中,施工单位应当每填筑一层就进行一次观测,如果,在设计作业过程中,相邻的两层的填筑时间超过了7d,在施工期间应当进行检测,从确保观测的时长不会超过5d,在实际观测期间,一旦发现发生了异常沉降现象,应当每隔2d进行1次观测,或者每天观测1此,从而实现对异常情况的密切观察,确保一旦出现异常情况,观测人员能够及时发现,以免造成更为严重的影响。在具体观测过程中,如果发现路基的沉降速小于1.0cm/d时,施工人员则可以进行一层土方填筑。在计算沉降速率时,应当精确到0.1mm。计算公式如下: b0=(∞,3,2,0,4,∞,5,2,3,4,0,5),b1=(0,3,4,5,1,0,∞,4,3,1,5,∞),b2=(5,∞,3,3,0,5,∞,0,2,4,4,1)。 序列集B的时频二维汉明自相关函数和汉明互相关函数分别为 由此可见,在碰撞区上[0,2]×[0,5]上,Hb0,b0(τ,ω)≤2((τ,ω)≠(0,0)),Hb0,b1(τ,ω)≤2,所以,Hm(B)=2,满足定理3,因此,序列集B是一个参数为(12,3,6,2,5,2)的最优TF-LHZ跳频序列集。 文献[13]基于交织法构造的跳频序列集关于理论界是最优的,而且得到的序列的数目更多,并引入了新的参数,但是,序列的构造只考虑了传输时延。本文基于交织法构造的跳频序列集是将最优TF-LHZ跳频序列集作为基序列集,与增加了新参数的移位序列交织得到了两类跳频序列集,并对新得到的两类跳频序列集的时频二维汉明相关性进行了严格的证明,得到了两类跳频序列集是最优TF-LHZ跳频序列集的结论。本文在构造跳频序列集的过程中不仅考虑了传输时延,还考虑了频率偏移,而且增加了新的参数,使跳频通信系统的跳频序列选择范围更宽。
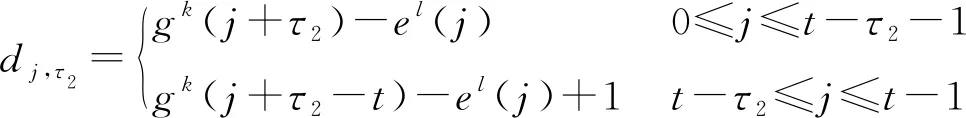
(0≤i0≠i1
(0≤r0≠r1

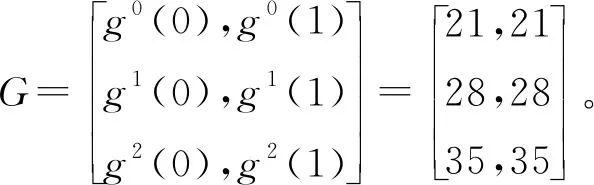
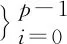

4 结论
