定积分的概念教学研究

吴凤珍

摘 要：定积分是工科高等数学教学的重点，无论从概念本身到实际应用，还是从计算方法到思想方法，均有着举足轻重的地位。本文对定积分的概念的教学做了深入的研究，突出了直观式、启发式教学，着重体现了数学文化和数学思想，不再拘泥于解题技巧.

关键词：定积分 概念 直观式 启发式 数学文化

定积分的概念是学习定积分的基础，它上承导数、不定积分，下启定积分的应用、重积分、曲线积分、曲面积分等.定积分的概念本身体现了微积分的基本思想方法-极限思想方法。通过定积分概念的学习，可培养学生抽象概括问题的能力、一定的逻辑推理能力、比较熟练的运算能力和自学能力，提高学生在数学方面的素质和修养。多年来的教学实践表明，定积分的概念的学习对学生来说是一个难点，这一部分内容是学生在大一学的，大二开设的数学后继课程及一些专业课中都要用到这一部分内容，但是到大二时，大部分学生都记不起定积分的核心思想，更谈不上用了。因此，如何进行定积分概念的教学，是一个很值得研究的课题.本文结合自己的教学实践，谈谈在定积分概念的教学中所采取的改革措施及体会。

一、复习极限思想，做好铺垫

极限贯穿于微积分的始终，是微积分的灵魂.定积分就是一种具有特定结构的极限，所以，不知道什么是极限，没有理解极限思想，就不可能理解定积分。学生尽管在此之前学过极限的定义及运算，也学过特殊的极限-导数，但真正理解极限思想的不多，在讲定积分的概念之前，必須先复习极限。在讲课之前，可通过问题导入复习极限。譬如，设计这样一个问题：已知变速直线运动的路程，如何求瞬时速度。大部分学生可能这样回答：瞬时速度就是路程对时间的导数，这时可进一步追问，什么是导数呢？它是如何产生的呢？让学生回顾导数的概念，进而加深对极限的理解，为定积分概念的学习做好铺垫。[1]

二、真正认识曲边梯形

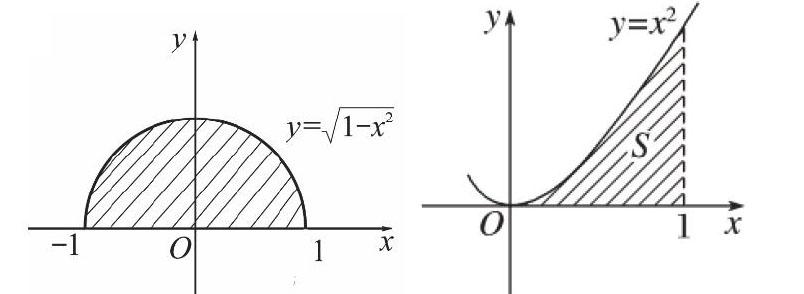
曲边梯形面积的求法是定积分部分的核心知识，而学生须先正确认识曲边梯形。对于标准的曲边梯形，学生往往能正确识别，而哪些不标准的，学生识别起来就比较困难。教学中，首先这样引入问题：我们已经会求三角形、矩形、梯形等规则的几何图形的面积，但是实际问题中遇到的图形往往是不规则的（展示一些不规则图形的图片），如何求不规则的几何图形的面积呢？最基本的规则图形是三角形，曲边梯形是最基本的不规则图形，那什么是曲边梯形呢？教师给出曲边梯形的定义，然后给学生展示一些具体的图片，让学生判断它们是否曲边梯形。通过具体的练习使学生明白，曲边梯形的两条互相平行的两条直边中的一条（或两条）可缩为一个点，但它的底边和曲边是必须存在的。像下面的两个图形也是曲边梯形。

还应使学生明确，有些规则的几何图形，也称为曲边梯形。譬如直角三角形、矩形、直角梯形。如果一个平面图形不是曲边梯形，可以通过作辅助线，将其面积化为曲边梯形面积的和或差，因此曲边梯形是最基本的平面图形，只要曲边梯形的面积会求了，任意平面图形面积的求解问题就解决了。[2]

三、直观演示，化抽象为具体

学生知道了曲边梯形的定义后，提出问题：如何求曲边梯形面积的精确值呢？请同学们回顾我国三国时期的数学家刘徽是如何求出圆的面积的精确值的。学生们都积极回答，这时播放割圆术的动画，引导学生总结得出结论：要求圆面积的精确值，先求其近似值，欲求整体的近似值，先求部分的近似值。如何求圆面积的近似值呢？数学家刘徽是这样做的：先把圆分割为许多小扇形，用三角形面积作为小扇形面积的近似值，再把所有小扇形的面积的近似值相加，就得到圆面积的近似值，这个近似值的精确度是与分割有关的，分割越细，近似值就越接近于精确值，因此，圆面积的精确值就是近似值当分割无限细密时的极限。以上过程归结为四个步骤：分割-近似-求和-取极限。在此基础上，师生共同分析类比得出曲边梯形面积的求解步骤。

求解步骤用数学语言表述如下：

[分割]在区间[a，b]中任意插入n-1个分点，

把区间[[a，b]分成个小区间

它们的长度依次为

过每个分点作平行于轴的线段，把曲边梯形分成个小曲边梯形。

[近似]在第个小区间上任取一点，用以为底，为高的小矩形面积近似代替这个小区间对应的曲边梯形的面积，类似地，其它每个小区间上对应的曲边梯形的面积都可以用小矩形面积代替。

[求和]把所有小矩形的面积加起来就得到大的曲边梯形面积的近似值，即：

[取极限]曲边梯形面积的精确值就是在分割无限细密条件下近似值的极限，如何用数学语言表示分割无限细密呢？有的同学说分割无限细密就是小区间的个数无限多，有的同学说分割无限细密就是小区间的长度无限小。到底哪种说法正确呢？这时再请学生仔细观察动画，并指出分割无限细密就是每个小区间的长度无限小，而不是小区间的个数无限多。并直观演示小区间的个数无限多与每个小区间的长度无限小不是等价的。例如固定一个小区间不动，把无限多个点都放在这个小区间外，这时就不能保证分割无限细密。如何表示无限细分呢？我们可以把每个小区间的长度计算出来，取其中最大的那个，记为：

则

关于变速直线运动的路程问题，引导学生类比解决。

四、概括共性，抽象定义

在分析完两个实例后，设置问题“如果我们抛开以上问题各自的实际意义，只从数学的角度看，这些问题有什么共性？”在学生回答之后师生共同总结出这两个实际问题的如下共性：

（1）解决的方法相同，都是采用极限的思想方法，先化整为零，再积零为整，用极限将近似转化为精确;

（2）处理的步骤是统一的，都是“分割、近似、求和、取极限”四步;

（3）所得结论的形式是一样的，都是一个特定结构的“和式极限”。

在自然界具有类似情况的实际问题非常普遍，比如变力作功问题，旋转体的体积，经济中的累积量等等，它们都可以归结为相同结构的和式的极限，由此就可以得到定积分的定义。[3]

定积分是一个十分抽象的概念，应强调以下几点：

（1）定积分中的“积”就是无限求和的意思，这个“积”是通过一个和式的极限来实现的。要求学生用极限思维来理解，明确这类问题的本质属性;

（2）这个和式的极限与区间的分法及的选取无关;

（3）定积分是一个极限值，只与被积函数和积分区间有关，与变量的选择无关，要与不定积分的概念区分开来。

对定义分析完之后，接下来设置问题：“定积分在几何上有什么意义？”有了前面的知识基础，学生们很容易回答这个问题。我们从面積问题开始又回到面积问题，紧扣主题，学生印象深刻。

五、介绍数学文化，激发兴趣

微分和积分是互逆运算，它们是从两个几何问题引出的，即求曲线切线的斜率引出导数，从求曲边梯形的面积引出积分。历史上积分的思想产生要早于微分，我国数学家刘徽（公元225年到公元295年），他的割圆术就包含了“无限细分，无限求和”的定积分思想，这种思想最早可追溯到古希腊数学家阿基米德提出的计算面积和体积的方法，后来逐步形成求面积、求曲线斜率的重要结论。但两者之间是彼此独立的，17世纪德国数学家莱布尼兹（1646年-1716年）和英国物理学家、数学家牛顿（1643年-1727年）才在前人的研究结果基础上创立了微积分学，将两者联系起来，从而使微积分得到了迅猛发展。

本节课改革了传统的教学方法，采用新的教学方法和模式，教学一开始先复习极限，然后再创设问题情境引入新课，符合学生的认知规律，在介绍完曲边梯形的定义之后，没有马上讲曲边梯形面积的计算，而是通过实例加深学生对曲边梯形的认识，为后面学习一般平面图形面积的计算扫清了障碍。在学习两个引例时，采用直观式、启发式、讨论式、类比的教学方面，化解了难点，收到了良好的教学效果。最后关于定积分数学文化的介绍更激发了学生的学习兴趣。[4]

参考文献

[1]同济大学应用数学系.高等数学（第4版）[M].北京：高等教育出版社，1996.

[2]华东师范大学数学系.数学分析（第2版）[M].北京：高等教育出版社，1991.

[3]金晶亮，等.高等数学课程中定积分概念教学设计[J].高等函授学报，2011，（5）：14-17.

[4]王彦军.高职学生定积分概念教学中的点滴体会[J].甘肃科技，2008，（17）：199-200.