关注运算能力发展的计算教学习题设计
2020-10-21宋晓春
宋晓春
(厦门市同安区第三实验小学,福建 厦门 361109)
计算教学中的习题,很多是纯粹的计算类练习,比如“口算”“列竖式计算”“脱式计算”等,其目标指向是训练学生的运算技能,提高学生运算的速度和正确率。这样的习题设计关注的仅仅是计算的结果,即停留在“会计算,能算对”的运算技能培养。这样的运算训练是机械的、重复的,往往给学生留下“计算枯燥无味”的印象,也容易导致学生思维刻板。在新课程改革以及关注学生核心素养培养的时代背景之下,数学习题设计不能仅仅关注运算技能,更要关注学生运算能力的培养。《义务教育数学课程标准(2011 年版)》指出:“运算能力主要是指能够根据法则和运算律正确地进行运算的能力。培养运算能力有助于学生理解运算的算理,寻求合理简洁的运算途径解决问题。”发展学生的运算能力,可促进学生理解运算意义,明晰运算原理,掌握运算方法,选择运算途径,学会正确、合理、灵活地计算。
一、丰富现实原型,促运算意义理解
运算意义是学生学习具体运算的基础,也是解决相关实际问题的依据。把握准确、深刻的运算意义,才能发展运算能力。运算意义的获得,是学生从现实原型出发,不断抽象、建构数学模型的过程。张奠宙教授指出,数学中的基本概念和基本算法都可以叫作数学模型,加减乘除都有各自的现实原型,它们都是以各自相应的现实原型作为背景抽象出来的。教师在设计习题时,可多提供丰富的现实原型,引导学生在辨析、比较、体验多种现实原型中寻找基本原型,不断抽象加、减、乘、除运算的意义。加法的原型可以是“合并”“移入”“增加”等,基本原型是“合并”;减法的原型有“剩余”“相差”“加法的逆运算”等,基本原型是“求部分数”;乘法的原型有“几个相同加数的和”“倍的问题”“面积”等,基本原型是“几个相同加数的和”;除法的原型有“平均分”“比率”或乘法逆运算等,基本原型是“平均分”。例如,教师可运用文字描述丰富的现实情境,提供以下现实原型:
以下四个问题中,不可以用25×5 这个算式解答的数学问题是( )。
A.三年级参加足球兴趣小组的有男生25 人,女生5 人,一共有学生多少人?
B.街道绿化工程,种了25 棵杨树,种的柳树是杨树的5 倍,种了多少棵柳树?
C.学生做操,每排站了25 人,排了5 排,一共有多少人?
D.一个长方形的长是25cm,宽是5cm,面积是多少平方厘米?
这些选项里有加法的现实原型,也有乘法的现实原型。学生在不同的情境中抽象出现实原型,教师进一步引导学生比较发现乘法的三种现实原型“几个相同加数的和”“倍的问题”“面积”的本质是相同的。比如B 选项中“倍的问题”,教师通过画图,让学生体会到“求一个数的几倍是多少”,即“求几个几是多少”,也就是“求几个相同加数的和”。D 选项中“长方形的面积”问题,引导学生回忆面积公式的推导过程,明晰求一个长方形的面积是多少,相当于求这个长方形可以摆几个边长1cm 的小方格,长方形的长相当于每排摆了几个,宽相当于摆了几排,长×宽相当于“每排摆几个×摆几排”,其实质也是“求几个相同加数的和”。由此,学生认识到乘法的基本原型是“求几个相同加数的和”,对乘法意义的认识更加深刻到位。
二、呈现多元表征,促运算原理明晰
学生不仅要“会算”,还要明白“为什么这样算”,即明白“算理”。算理是运算的原理。曹培英指出,算理是运算能力的核心成分,它与算法构成运算能力的“一体两翼”。以往的习题设计更多的是关注学生计算的结果,关注学生计算的准确率,忽视对学生计算过程的关注,忽视学生是否真正理解算理而不只是机械地计算。教师在进行计算习题设计时,呈现多种表征方式,引导学生聚焦不同的表征方式背后相同的算理,促进学生对算理结构化的理解。下面以“两位数乘两位数的笔算乘法”的习题设计为例。
1.与口算勾联
口算是竖式计算基础,有些口算的过程和竖式计算的算理在本质上是一致的。这时,可以对比口算与竖式计算,沟通两者的联系,进行勾联。习题设计如下:
下面是小明口算一道题的过程。请问,他计算的乘法算式是( )
16×10=160
16×2=32
160+32=192
2.与直观模型勾连
在算理教学过程中,往往要借助一定的直观模型帮助学生理解算理。这些直观模型有小棒、计数器、点子图、格子图、数轴等。在习题设计时,可以将竖式与直观模型勾连,以促进学生对算理的领悟。习题设计如下:
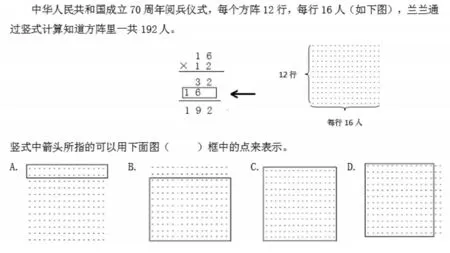
3.与具体情境勾连
在具体的情境中理解列竖式计算每一步的含义,让学生对算理的理解有了情境的直观化依托。习题设计如下:
陈师傅平均每小时做19 个零件,那么工作13 小时做了多少个零件?在下列竖式中箭头表示( )
A.工作3 小时做了190 个零件。
B.工作10 小时做了19 个零件。
C.工作10 小时做了190 个零件。
D.工作13 小时做了190 个零件。
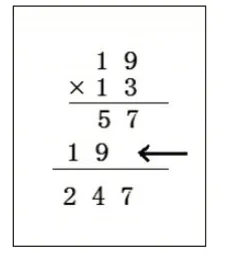
4.在“去情境化”中抽象
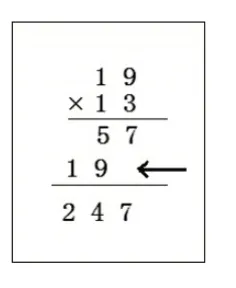
习题设计时,抛开口算、直观模型、情境等依托,从算理本质入手,直接用数学语言进行表征算理。这就是“去情境化”练习,可以提高学生对算理的抽象化理解水平。习题设计如下:
在19 乘13 的竖式中,箭头这一步表示的是( )
A.10 个19 的和
B.13 个19 的和
C.1 个19 的和
D.3 个19 的和
三、重视理法融合,促运算方法掌握
算法是计算的程序和要领,重在对算理的提炼和总结。算理和算法相互融合,共同支撑运算能力的形成。习题设计时,重视算理算法相互融合,促进学生掌握运算方法。
1.加强算法的比较
计算算法多样化,可以加强不同算法之间的比较,分析异同点,在比较分析中进一步聚焦计算本质。如“三位数乘两位数”的计算,可以运用“格子乘法”和“多层列竖式”法,请学生观察对比,习题设计如下:
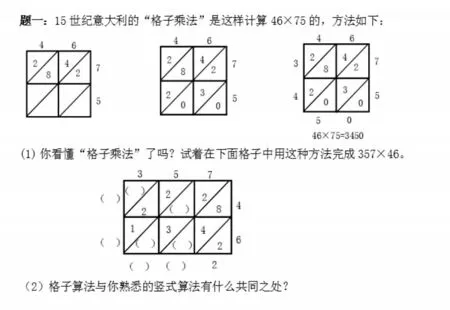

以上两题借助数学史上的算法,开阔学生的视野,同时引领学生观察、比较、分析“与熟悉的竖式算法”的异同点,促进学生理解笔算乘法内在的本质。不管是哪种方法,实质都是将拆分成的几个几、几十个几、几百个几等用竖式加以记录,本质上都是相同计数单位的累加。
2.突显算法的“关键步骤”
算法中有“关键步骤”,习题设计时可以突显“关键步骤”,在关键处理法融合,在关键处强化训练,使学生掌握算法,不易出错。如“三位数除以一位数的笔算”算法是:从被除数的最高位除起,如果最高位不够除,就看被除数的前两位,除到哪一位时,商就写在哪一位上。在计算过程中,关键的一步是“判断商的最高位”。这是计算的第一步,为顺利进行接下来的计算奠定基础。针对这个“关键步骤”,教师可以先设计习题“要使口76÷6 的商是两位数,口中最大能填()”。学生在观察、讨论、交流的基础上,小结出“被除数的最高位大于或等于6 时,商是三位数;被除数的最高位小于6 时,商是两位数”。教师追问为什么,引发学生深思并理解“被除数的最高位小于6 时,不够1个百,商的最高位只能在十位”。由此,算理算法相融,促学生深刻理解“判断商的最高位”的方法。接着,教师设计“不计算,快速判断下面的商是几位数”的习题,进一步强化训练,使学生真正掌握“判断商的最高位”的方法。
四、引导比较分析,促运算途径选择
学生在解决纯运算问题,或者在解决实际问题的运算决策与实施过程中,能根据问题的条件寻找并设计合理、简捷的运算途径,这是学生运算能力发展的表现。教师在习题设计时,应增强学生的比较意识,使学生对问题的不同运算途径能够及时分析比较,选择合理、简捷的运算途径。
1.改变习题设计的指导语
以往经常用“口算”“估算”“笔算”“脱式计算”等指导语为学生指定运算途径,导致学生不需要思考就可以解决问题,或者满足于一种运算途径,造成思维“僵化”“程式化”。教师可以将习题设计的指导语改为“选择你喜欢的方法进行计算”“你认为怎样简便就怎样算,记录你的计算过程”“如果不列竖式,还可以怎样算”等,给学生自主思考、自主选择运算途径的机会。同时,教师调整跟进相应的评价标准,促进学生对比反思“解决这一个问题有哪些方法?哪个方法最简捷?”等。
2.增加分析比较类习题
“计算”并不是一项机械化的工作,计算中也蕴含着观察、推理、分析、比较等思维成分。教师设计分析比较类的习题时,可引领学生感受单纯的“计算”并不是解决问题的唯一方法。解决问题的运算途径多样化,增强学生计算过程中分析思考的意识,积累丰富经验,避免思维定式。如“判断错题和连线找算式”这两种题型,要求学生不要列竖式计算,而是运用自己的计算经验进行分析、判断、说明。学生可以运用乘积个位上的数字特征、估算比大小等多种策略进行综合分析,充分体验到不需要列竖式计算也可以快速作出判断,其观察能力、推理能力、估算能力、计算思维都得到发展。
题一:205×42=6023
不列竖式计算,请判断上面这题是否出错?写出你的判断依据。
题二:不列竖式计算,直接判断。(将左边算式与右边对应的计算结果连起来)
75×48 1794
26×69 3600
36×69 972
82×11 2484
81×12 902
总之,运算能力是在学生数学核心素养培育背景下提出来的一种重要的数学能力。教师在计算习题设计时,关键要发展学生运算能力,实现正确、合理、灵活地计算。
