基于自抗扰的无刷直流电机控制系统研究

欧阳名三 闫中文

（安徽理工大学，安徽 淮南 232001）

无刷直流电机在电动车、机器人、航空航天等领域内都有着广泛的应用[1]。随着应用领域的不断发展延伸,各种控制策略和算法也不断的出现,传统PID算法在无刷直流电机的强耦合性方面的控制效果不够理想[2]。控制过程中存在响应速度慢、调节时间长、超调量大等问题[3]。因此，一些新的控制算法被人提出来。文献[4][5][6]中采用模糊PID控制器，但模糊PID控制器参数计算量较大，往往控制过程不是很容易实现。自抗扰自适应控制算法是在改进PID算法缺陷基础上结合现代控制理论提出的一种新型控制算法[7，8]，其特点是具有天然的解耦性，以及几乎和模型无关等，非常适用于无刷直流这类具有强耦合性的控制系统。

一、BLDCM的数学模型

无刷直流电机控制系统为两两导通方式，其电压平衡方程为[9]：

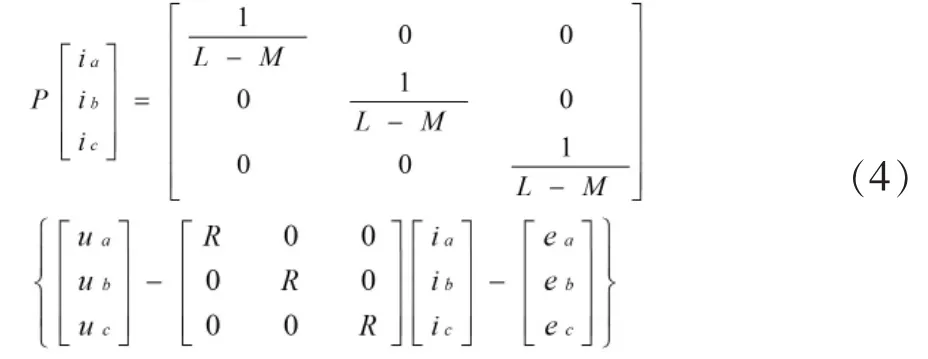
式中，Ua，Ub，Uc为相电压，ia，ib，ic为相电流，R 为电阻，L、M 分别为自感及互感 ea，eb，ec反电动势。

电磁转矩方程为：

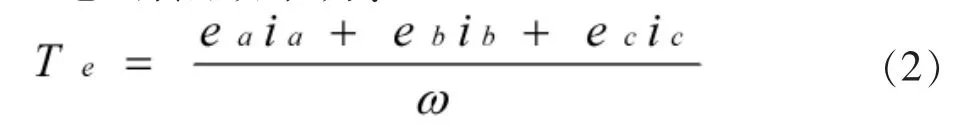
式中，Te为电磁转矩(Nm)，ω为机角速度(rad/s)。

运动方程可表示为：

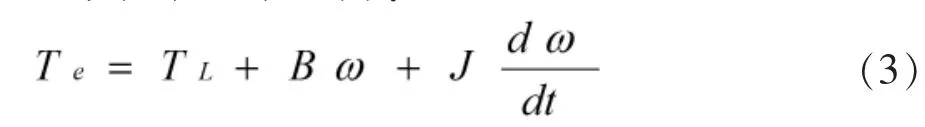
式中，TL为负载转矩(Nm)，B为阻尼系数(Nm·s/rad)，J为转动惯量(kg·m2)。

由（1）式当中的电压方程变形可得BLDCM的状态方程。

二、自抗扰控制器（ADRC）的设计

自抗扰控制是在改进经典PID固有缺陷的基础上，而逐步形成的新的控制策略（或控制算法），其优点是对控制系统对象的模型不依赖[10]，对扰动适应性较强，而且鲁棒性以及可操作性也非常好。

（一）自抗扰控制器组成

自抗扰控制器分为跟踪微分器（Tracking Differentiator）、非线性状态误差反馈控制器（Nonlinear State Error Feedback law）以及扩张状态观测器（Ex-tended State Observer）三个部分，其基本结构图如图1 所示[11]。

图1ADRC结构图

跟踪微分器(TD）：对系统的初值进行安排过渡过程，能够得到v的近似值v1和v的微分v2。无论v是何种状态，通过跟踪微分器(TD）都能使v1和v2连续，能够解决超调和响应速度问题。

扩张状态观测器（ESO）：根据扰动状态观测的思想，把对输出有影响的扰动变量扩张成一个新的状态观测变量，建立一个能够准确地观测扩张后状态变量的观测器，即为扩张状态的观测器。扩张状态观测器并不需要依赖于扰动的模型，也不需要直接测量扰动就可以得到扰动的估计值。

非线性状态误差反馈控制器（NLSEF）：通过跟踪—微分器系统能够产生过渡过程的误差信号和误差微分信号，并且能够生成误差积分信号，将三种控制信号按一定的控制规律互相组合起来，形成了组合的控制器。三种信号既可以互组合成和PID控制相似的线性组合控制器，也能组合成独特的非线性控制器。

（二）ADRC数学模型

1.TD的数学模型

其中x1用于跟踪信号v(t)，x2用于跟踪v(t)的导数，其中 x1、x2和 v1、v2一样，一个用于跟踪信号，一个是微分信号。fst是如下的非线性函数。

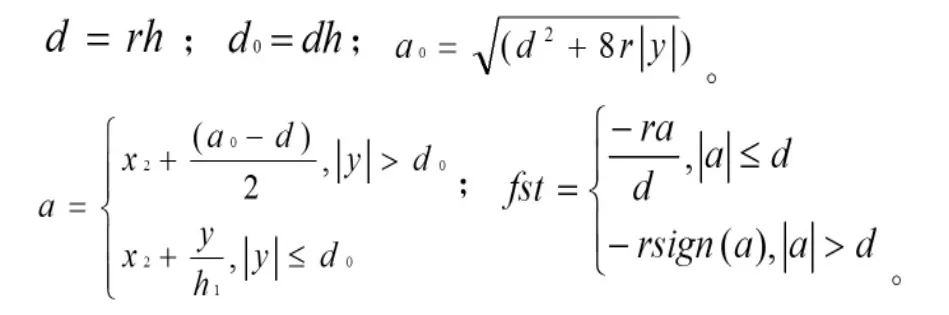
式中，h是数值积分的步长，r是跟踪速度的参数，h1是噪音滤波效应的参数。

2.ESO的数学模型

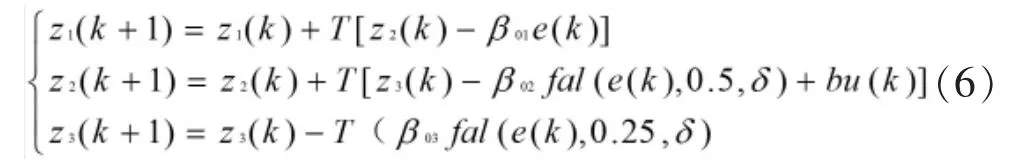
z1(t)，z2(t)为状态变量的估计。z3(t)而对不确定模型和外扰的进行估计。β01，β02，β03和 b 是可调参数。δ为滤波因子。δ的取值范围一般为：5T≤δ≤10T。

fal为非线性函数。

3.NLSEF的数学模型

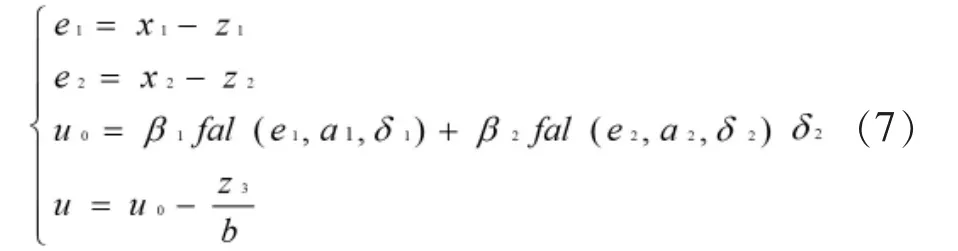
其中 α1，α2，β1，β2，δ1，为可调参数。

（三）无刷直流电机自抗扰控制系统设计

将无刷直流电机作为被控制对象，将自抗扰输出信号u作为无刷直流电机的输入。其基本结构如下所示。

图2 无刷直流电机系统框图

当无刷直流电机的输出信号y小于输入信号v时，扩张状态观测器（ESO）观测出正的误差信号e，扩张状态观测器输出的z1(t)，z2(t)减小，而z3(t)增大。由于输入信号v是不变的，误差信号e1，e2以及u0会增大，u也会随之增大，最终输出信号y会增大。输出信号y增大使误差信号e减小，fal函数值大于零的区间也会减少，控制u的速度变慢。输出信号的调节也变慢，反之当无刷直流电机的输出信号y大于输入信号v时，扩张状态观测器（ESO）观测出负的误差信号e，扩张状态观测器输出的z1(t)，z2(t)增大，而z3(t)减小。由于输入信号v是不变的，误差信号e1，e2以及u0会减小。u也减小，输出信号v也会减小。输出信号的减小会使误差信号e增大，fal函数值小于零的区间也会增大，控制u的速度变快。输出信号的调节也变快，经过上述调节，最终实现无刷直流电机的控制。

三、仿真模型的建立

在matlab中,借助于simulink环境下s函数，通过使用c语言或m语言将自抗扰的数学模型转换成了离散算法,写进s-function模块中，设置好参数，得自抗扰控制的无刷直流电机控制系统的仿真模型如图3所示。

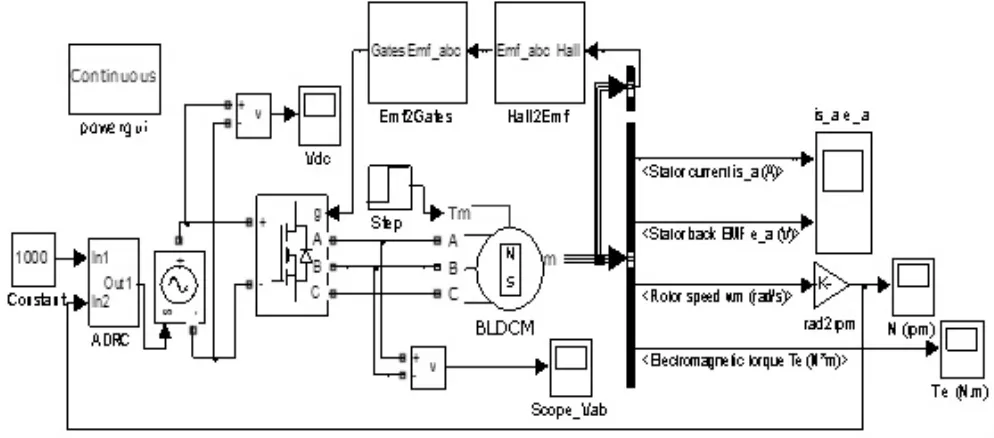
图3 无刷直流电机自抗扰控制系统仿真模型

仿真过程中无刷直流直流电机参数设置如表1所示：

表1 电机参数

自抗扰控制器参数整定根据经验法可得数据如表2所示：

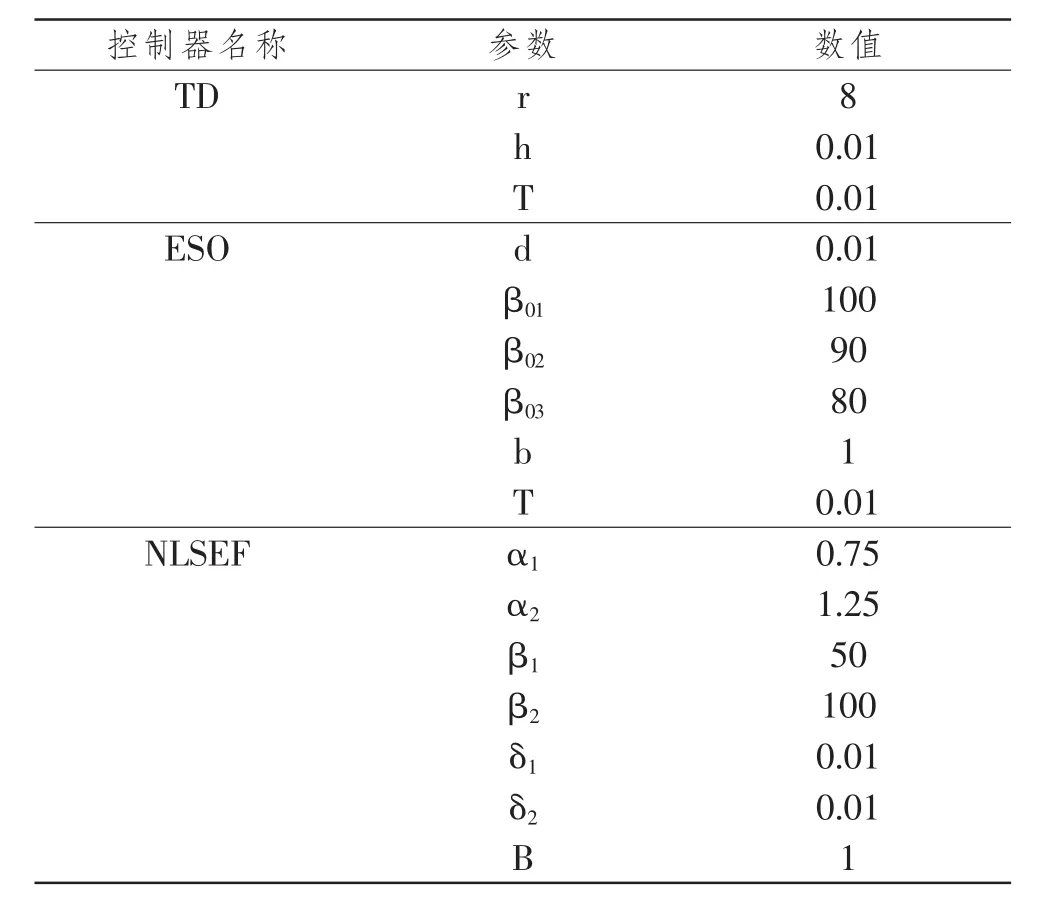
表2 自抗控制器参数

四、仿真结果及分析

（一）起动和突加负载实验

无刷直流电机转速的设定值为n=1000 r/min，在仿真时间t=0.1s时，给无刷直流电机加TL=1.5 N·m负载，然后分别对传统PI控制和自抗扰控制下的无刷直流电机进行仿真实验，得到无刷直流电机转速仿真波形如图4所示。

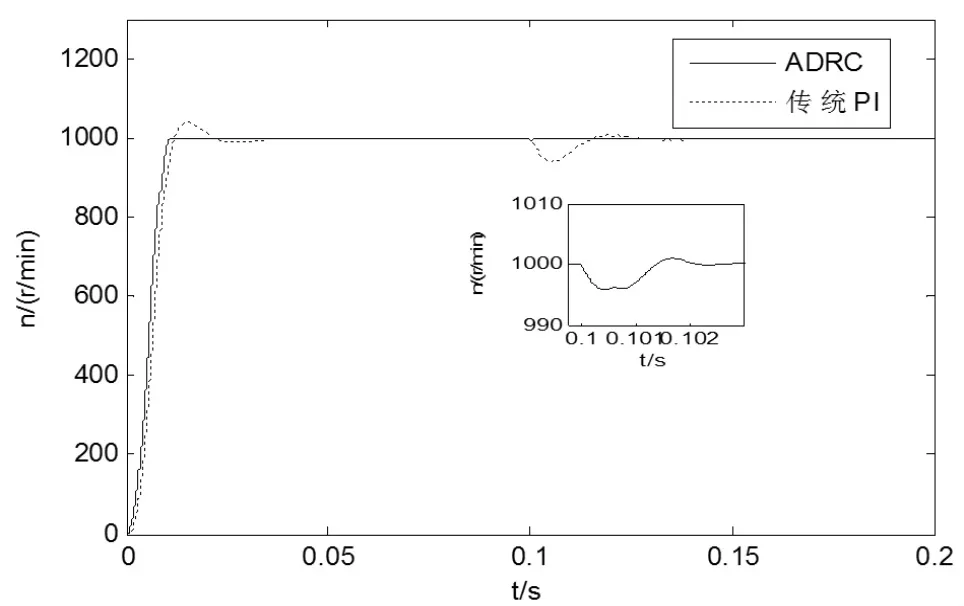
图4 突加负载时转速仿真图形

图（4）中内部图形是ADRC曲线在0.1s时放大部分。由仿真波形图可知，传统的PI控制算法在t=0.05s时，无刷直流电机转速达到稳定状态，转速最大时为1040r/min,超调为4%。而自抗扰控制算法在t=0.01s时无刷直流电机的转速就已经稳定了，超调几乎为0。系统在0.1s由于突加负载转矩的作用，传统PI控制在0.03s后转速才能够恢复，转速最大下降到940r/min。超调为6%。而自抗绕控制在0.003s转速就能恢复了，转速下降到995r/min,超调仅为0.5%。

（二）改变速度给定实验

无刷直流电机转速设定值n=1000 r/min,在时间t=0.1s时，电机转速由n=1000 r/min,突然下降为n=800 r/min，分别对传统PI控制和自抗扰控制下的电机控制系统进行仿真实验，得到电机的转速仿真波形如图5所示。

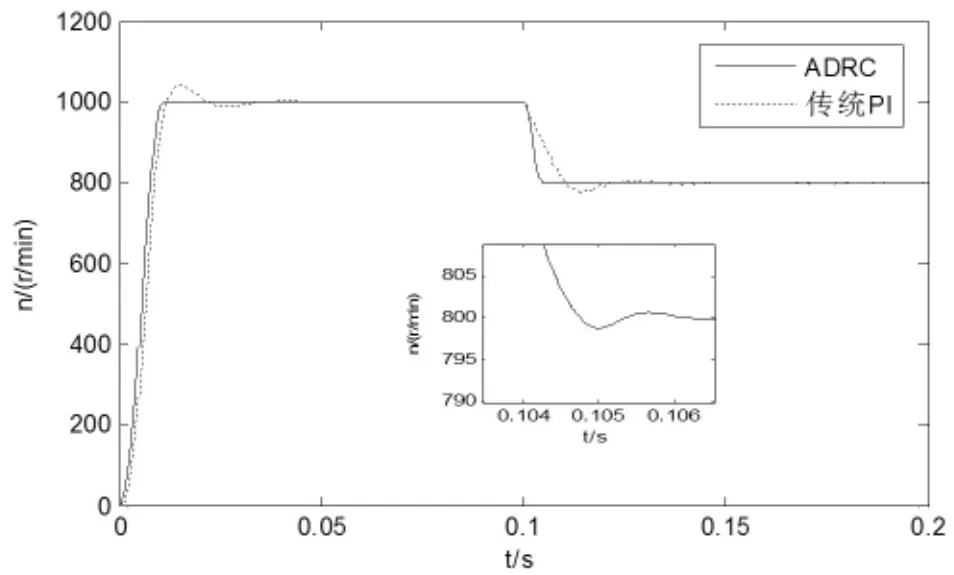
图5 转速突变时转速仿真图形

图5中内部图形是ADRC曲线在0.1s左右时放大部分。从图中可知传统PI控制在转速突变时系统在t=0.025s后达到稳定，转速下降到775r/min，超调为2.5%，而自抗扰控制在转速突变时系统t=0.007就能够稳定，转速下降到798r/min超调0.2%。

通过仿真结果对比可以看出：

启动时自抗扰制器比传统PI控制器响应速度更快，调节时间更短，且无超调。突加负载或转速突变时，自抗扰制器比传统PI控制器不但具有较快的响应速度，而且对扰动适应性较强，鲁棒性以及可操作性也非常好。

五、结论

针对传统的PID算法控制下的无刷直流电机转速抗干扰能力差、响应速度慢的问题，提出了采用自抗扰控制器来对无刷直流电机进行控制，搭建了无刷直流电机自抗扰控制的仿真模型，并与传统的PID控制算法同时进行了对转速控制的仿真实验并分析对比，仿真实验的结果表明：自抗扰控制器不但响应速度快，而且对扰动适应性较强,鲁棒性以及可操作性也非常好。