地上输料通道对浅圆仓仓壁和通道受力的影响

孙巍巍，冯 君，朱建平，张栩东，易建荣，王 磊

（1. 南京理工大学土木工程系，南京 210094；2. 南京理工大学瞬态物理国家重点实验室，南京 210094；3. 中国中材国际工程股份有限公司（南京），南京 211100）

0 引 言

浅圆仓作为一种储存散装物料的构筑物，广泛用于粮食、化工、制药等农业和工业工程领域[1-3]。地下通道作为浅圆仓内贮料运出的重要设施，内安装有卸料输送机及配套的强电、弱电电缆[4]。当地下通道防水材料出现老化，输送设备容易受到腐蚀，将影响筒仓的正常运行，甚至威胁工作人员的安全[5]。为方便后期维护，将原本位于地下的输料通道上移，出现地上输料通道工艺。地上输料通道进入了浅圆仓内部，势必对仓壁和通道的受力产生影响[6-9]。地上输料通道筒仓多应用于高径比介于0.4～1.0 的浅圆仓，即欧洲筒仓规范 EN 1991—4：2006中定义的Squat Silo，国内外筒仓规范中未发现针对地上输料通道的具体设计条文[10-14]。国内筒仓标准 GB 50077—2017[10]提出的地下输料通道设计方法主要基于“隧道理论”[15]，虽然在岩土中开挖形成的隧道与埋入贮料和回填材料中的通道在形式上较为类似，但二者的受力环境存在很大差别，隧道土拱效应[16]是否同样适用于输料通道的压力预测仍需要进一步研究。

缩尺模型筒仓装卸料试验[17-18]作为一种研究手段，近年来被众多研究人员所采用。张大英等[19]利用有机玻璃筒仓模型研究了立筒仓卸料过程中的侧压力变化，发现筒仓内存在超压现象，但各测点超压系数不同。张翀等[20]开展了落地式钢筒仓模型的卸料试验，证实了偏心卸料对仓壁受力性能产生了巨大影响。韩阳等[21]基于仓体的微缝分离设计研制了缩尺模型筒仓试验装置，并开展了静态储粮下仓壁摩擦力试验研究。目前尚未发现地上通道筒仓缩尺模型装卸料试验数据和报道。

为准确研究地上输料通道对浅圆仓仓壁和通道受力的影响，本文拟开展地上输料通道浅圆仓缩尺模型装卸料试验研究，重点考察不同偏心率、不同高径比下仓壁和通道上压力分布及超压演化规律，并与筒仓标准 GB 50077—2017 有关规定开展对比分析，拟为浅圆仓仓壁和通道结构设计提供一定的参考和借鉴。

1 设备与方法

1.1 试验设备

以地上通道筒仓结构（图 1a）为工程原型，制作了如图1b 所示的地上通道筒仓缩尺模型。采用流动性较好的标准石英砂作为贮料和回填材料，经前期直剪测试[22]其内摩擦角φi和休止角φr均为 33°，容重γ为 14.4 kN/m3。为方便观察筒仓内贮料流动通道变化，以 3 种不同高度的透明有机玻璃圆筒用来模拟仓壁，圆筒外径为1 000 mm，壁厚为 10 mm，高度h1分别为 392、642、892 mm。3 条不同长度的地上输料通道采用厚度 10 mm钢板制作，分别为1 条主通道和2 条次通道。其中主通道条带偏心率为0，2 条次通道条带偏心率es/dn均为0.31（条带偏心距es=300 mm，筒仓内径dn=980 mm，图2）。通道高度hc为70 mm、宽度bc为90 mm，在其顶壁每隔100 mm 对称开设直径35 mm 卸料洞口。有机玻璃圆筒和地上通道均安置在试验钢支架上。

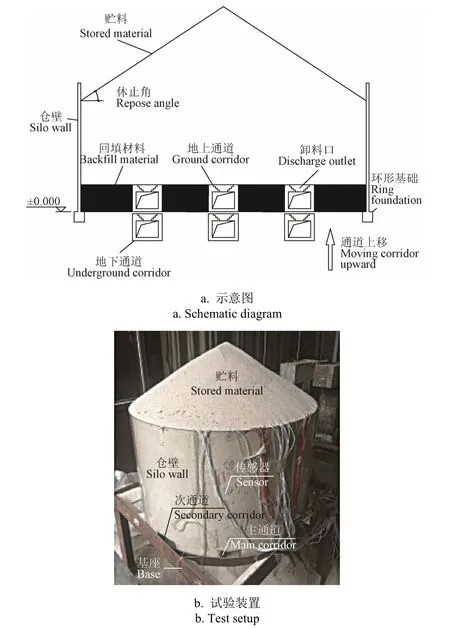
图1 地上通道筒仓示意图及缩尺试验布置Fig.1 Schematic diagram of ground corridor silo and reduced-scale test setup

如图 2 所示，仓壁和通道上均布置了经标定的溧阳市超源仪器厂BW45-0.02 型电阻应变式压力计，仓壁压力计沿环向0°～180°范围内每45°布置一列，共5 列；压力计沿仓壁高度自下而上间距为120 mm，但因主通道的阻挡，0°和 180°方向上最下端未设置压力计。通道侧壁的压力计位于通道高度中点处，与卸料洞口位置保持一致，顶壁的压力计则分布于通道轴线上。沿通道方向定为X轴，垂直通道方向定为Y轴，坐标原点位于筒仓底面的圆心处。为准确定位压力计，每个压力计均有相应的编号。仓壁压力计编号由 3 个数值组成，第一个数值代表高径比；第二个数值代表压力计所在的环向角度，（o）；第三个数值表示压力计距离筒仓底部的垂直距离，mm。DH3816N 应变测试仪结合配套软件用于压力数值的采集[23]。

图2 筒仓模型压力计布置俯视图Fig.2 Top view of silo model pressure gauge layout

1.2 试验方法

整个装卸料试验以圆筒高度h1等于642 mm 的筒仓模型为主，其实际高径比hn/dn等于 0.69（贮料计算高度hn=678 mm，计算至通道顶壁），并对其他 2 个高径比（hn/dn=0.44, 0.95;hn分别取428 mm, 928 mm 时）的筒仓开展了对比分析。卸料过程中，当压力计获得的卸料压力大于初始装料静态压力时，则认为筒仓内存在超压现象[24]，并将卸料过程中的压力最大值与初始静态压力的比值定义为超压系数Cd。当卸料过程中，无超压现象，则超压系数Cd等于1.0。

1.2.1 装料试验

在浅圆仓模型中共放入 3 条主次通道，采用人工加料方式，加料时首先堵上所有通道顶壁洞口，从模型顶部加料至满仓状态，待贮料完全稳定且压力计数值平稳，读取相关压力数据。

1.2.2 卸料试验

为考虑偏心率的影响，在主通道顶壁设置了#1～#5卸料口（图2）用于模拟从中心卸料（卸料偏心距e=0）到偏心卸料（e=100 mm、200 mm、300 mm、400 mm）的变化过程。装料试验完成后，单独打开主通道上某一卸料口完成卸料试验，并采集压力数据。

2 结果与分析

2.1 装料试验

图3a 表明满仓状态下仓壁侧压力（ph,w）随着压力计埋深的增加基本上保持线性增长，但通道高度以下仓壁侧压力曲线出现了明显的弯折。相对而言，垂直于通道的90°方向仓壁侧压力受到通道的影响稍小于45°方向和135°方向。这些现象在其他2 个高径比（hn/dn=0.44, 0.95）的浅圆仓装料试验中同样可以观察到，显然通道的存在影响了仓壁底部的静载侧压力分布。

图3 装料测试结果（hn/dn=0.69）Fig.3 Loading test results (hn/dn=0.69)

如图3b 所示，主通道的顶壁和侧壁压力沿通道轴线不断变化，越接近筒仓边缘（仓壁）压力值越小，越接近筒仓中心位置压力值越大。这一现象可以解释为贮料顶部锥体的存在，造成了通道各点实际贮料高度H（计算点竖直向上投射到贮料锥形顶的距离，从通道顶壁算起）不同[12]。次通道的顶壁和侧壁压力的分布规律和主通道类似。

2.2 卸料试验

2.2.1 不同偏心率

以偏心率e/dn为0.31（e=300 mm）的筒仓偏心卸料试验为代表，进行详细阐述。如图4 所示，装料完成后，单独打开主通道#4 卸料口（e=300 mm），在卸料口的正上方逐渐形成一个倒锥面，倒锥面和水平面的角度约等于贮料内摩擦角φi，不断下切倒锥的顶点始终位于#4 卸料口的正上方。整个卸料过程可以归纳为一个倒锥不断下切的过程[25-27]。因为偏心效应，偏置下切倒锥不是一个完整的锥体，贮料和仓壁的交线沿圆周方向高度存在明显差异，卸料口近端（0°方向）仓壁的贮料高度明显小于卸料口远端（1 8 0°方向）仓壁的贮料高度。

为清晰的标识和观察卸料开始后的超压现象，卸料开始前的装料稳定状态以时间负值的方式记录在压力图中。如图 5 所示，偏心卸料开始后随着偏置倒锥的不断下切，中上部贮料不断排出筒仓，仓壁中上部的部分压力计逐渐归零，例如压力计0.69-0°-620 在约50 s 归零。仓壁与贮料交线的不断变化，仓壁各方向上的侧压力变化各异，卸料口近端（0°方向）侧压力迅速下降，而远离卸料口一侧（180°方向）侧压力缓慢下降，其他角度介于二者之间。由此可见，越接近卸料口的仓壁侧压力下降越迅速，越远离卸料口的仓壁下降越缓慢。偏心卸料结束后筒仓模型中存在“死料”区域，从而部分仓壁和通道上的最终压力值并不为零。

整个卸料过程中仓壁超压现象不明显，且普遍超压持续时间很短。例如压力计0.69-0°-380 测试值在卸料初始瞬时增加后，仅仅维持了 2 s 后，急速下降转入欠压状态（卸料压力小于初始静态压力）。只有极少数压力计（例如0.69-180°-140）维持了较长时间的超压现象，且超压系数Cd（最大卸料压力/初始静态压力）只有1.032。

偏心卸料开始后，主通道顶壁（MT）靠近#4 卸料口的MT250 和MT450 压力值迅速减少，其他顶壁部位出现小幅超压。主通道的侧壁（MR）、次通道顶壁（ST）和右侧壁（SR）压力值变化较小，只出现了微小的超压，保持缓慢的阶梯状压力下降，但靠近#4 卸料口的次通道左侧壁（SL）超压仍然明显，超压系数Cd可达 1.154，详见图6。相较于仓壁，通道顶壁和侧壁的超压现象更加明显，且普遍超压持续时间较长。

图4 偏心卸料过程（e/dn=0.31）Fig.4 Eccentric discharge process（e/dn=0.31）

其他卸料偏心率e/dn下的试验现象整体类似，只是仓壁和通道上的超压系数Cd有所变化。表1 给出了4 个不同偏心率e/dn偏心卸料和中心卸料下仓壁各方向上超压系数Cd的对比。总的来说，偏心卸料下仓壁存在不同程度的超压现象，Cd整体规律性不强，并没有观测到Cd随着偏心率e/dn增大而增大的现象，超压系数最大值（Cd=1.19）出现在偏心率e/dn等于0.1。仓壁的超压部位主要集中在仓壁中下部，当偏心率e/dn较小时，超压部位主要出现在0o和180o方向上，偏心率e/dn较大时，超压部位则主要出现在90o方向。

图5 偏心卸料下不同角度的仓壁侧压力（e/dn=0.31）Fig.5 Lateral pressure of silo wall with different angles under eccentric discharge(e/dn=0.31)

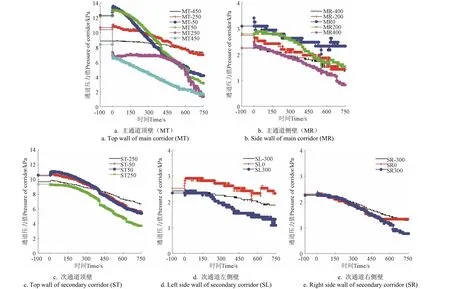
图6 偏心卸料下通道压力（e/dn=0.31）Fig.6 Corridor pressure under eccentric discharge（e/dn=0.31）

如表 1 所示，不同偏心率下的试验结果均表明卸料通道更为直接的受到贮料的动态冲击，通道的超压系数普遍大于仓壁超压系数。主通道顶壁（MT）紧邻卸料口部位一般不会出现超压现象，相反离卸料口稍远距离的通道顶壁呈现明显的超压现象，距离更远处超压现象开始衰减；主通道侧壁（MR）的超压现象在卸料口附近最为严重；次通道顶壁（ST）和右侧壁（SR）超压现象基本可以忽略；次通道左侧壁（SL）因直接面对卸料口，出现了明显超压，超压系数最大值集中在通道中部。

2.2.2 不同高径比

试验结果表明 3 个不同高径比（hn/dn=0.44、0.69、0.95）筒仓的贮料偏心卸料（e/dn=0.31）流动过程类似，只是筒仓的容量大小决定了卸料时间的长短。如表 2 所示，不同高径比对于超压系数Cd影响较大，高径比hn/dn在0.69 以下时，超压系数Cd较小，均在1.2 以下，且在各个方向上无明显规律；但高径比hn/dn接近1.0 时，超压系数Cd迅速上升，特别在靠近卸料口的 45o方向上达到了1.40。

表1 不同偏心率下仓壁和通道超压系数Table 1 Overpressure coefficients of the wall and corridor under different eccentricity ratios

如表 2 所示，通道超压系数Cd随着高径比hn/dn的变化规律与仓壁类似，当高径比hn/dn在0.69 以下，主通道的顶壁（MT）和侧壁（MR）及次通道的顶壁（ST）和左侧壁（SL）的超压系数小幅增长，但高径比hn/dn接近 1.0 时，超压系数Cd迅速增加。但次通道的右侧壁（SR）超压系数Cd随着高径比hn/dn的增加呈下降趋势。

2.3 测试结果与规范预测值对比

2.3.1 仓壁结果对比

由图3a 可知，仓壁侧压力测试值与标准GB 50077—2017 预测值（式（1）、（2））在通道高度以上符合较好，而在通道高度范围内的仓壁侧压力测试值明显小于规范预测值，这一结论也同样适用于其他两个高径比（hn/dn=0.44, 0.95）的浅圆仓。

式中：ph,w1为通道顶壁以上贮料产生的仓壁侧压力，kPa；ph,w2为通道顶壁以下回填材料产生的仓壁侧压力，kPa；k为侧压力系数；φi为贮料或回填材料的内摩擦角，（o）；γs为贮料的容重，kN/m3；γb为回填材料的容重，kN/m3，缩尺试验中回填材料采用了贮料石英砂；hn为贮料计算高度，m；s1为贮料锥体重心至计算截面的垂直距离，m。s2为通道顶壁至计算截面的垂直距离，m。

表2 不同高径比下仓壁和通道超压系数Table 2 Overpressure coefficients of the wall and corridor under different aspect ratios

标准 GB 50077—2017 中对于高径比hn/dn介于0.4～1.0 的浅圆仓中心卸料时，仓壁不考虑水平压力修正系数Ch，可以看作1.0。对于偏心效应，设计人员常用标准 GB 50077—2017 中的偏心卸料压力系数Ecc=(dn+4e)/(dn+2e)修正静态压力。图 7 给出了考虑偏心效应后的浅圆仓仓壁超压系数（Cd=Ecc）的预测值与缩尺试验的测试值对比，可以发现，卸料偏心率较小时（e/dn<0.2），缩尺试验超压系数测试值稍大于标准GB 50077—2017 的预测值；卸料偏心率较大时（e/dn≥0.2），标准 GB 50077—2017 的超压系数预测值基本偏于安全。

图7 仓壁超压系数测试值与预测值的对比Fig.7 Comparison between the test value and the predicted value of the overpressure coefficient of silo wall

2.3.2 通道结果对比

标准GB 50077—2017 借鉴“隧道理论”[28-30]将输料通道分为浅埋和深埋两类。判断依据：1）贮料高度H与通道截面宽度bc之比小于1.5 为浅埋，大于等于1.5 为深埋；2）贮料高度H与地道卸料拱高度hg之比小于等于5为浅埋，大于5 为深埋。其中第2 条依据为通道深埋的必要条件。贮料高度H在标准GB 50077—2017 通道静荷载示意图中定义为贮料锥形顶重心到通道顶壁。根据以上判断原则，以主通道为例，筒仓（hn/dn=0.44）的主通道为浅埋，筒仓（hn/dn=0. 69，0.95）的主通道为深埋。

依据标准GB 50077—2017，深埋条件下通道顶壁压力pv,c1按照式（4）计算；浅埋条件下通道顶壁压力pv,c2按照式（5）计算，通道侧壁压力ph,c按照式（6）计算。

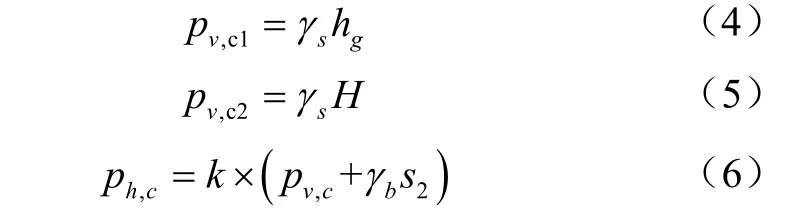
式中hg为卸料拱高度，m，hg=0.5lg/f；lg为卸料拱的跨度，m，lg=bc+2hctan(45o-φi,b/2)；hc为通道高度，m；bc为通道宽度，m；f为贮料的内摩擦系数，f=tan(φi,s)；φi,s为贮料的内摩擦角（o）；φi,b为回填材料的内摩擦角（o）；pv,c为深埋或浅埋条件下的通道顶壁压力，kPa。

如图3b 所示，标准GB 50077—2017 将顶部贮料锥体等效为圆柱体后，贮料高度H恒定为贮料计算高度hn，无法反应沿通道轴线贮料高度的变化[12]，更为严重的是通道被判定为深埋时，通道压力预测值明显小于测试值，偏于不安全。而主通道顶壁及侧壁的压力（pv,c,ph,c）分别依据浅埋公式（5）和公式（6）的理论值和试验测试值符合较好，其中公式（5）中贮料高度H应取为通道计算截面的实际贮料高度。其他两个高径比（hn/dn=0.44,0.95）浅圆仓主次通道顶壁及侧壁的压力分析同样证实了以上结论。因此建议浅圆仓（hn/dn=0.4～1.0）的输料通道不区分浅埋和深埋，均按照浅埋公式（5）和公式（6）分别计算主次通道顶壁及侧壁的压力。

目前通道顶壁和侧壁设计时往往不考虑超压系数，但试验结果表明通道顶壁和侧壁均出现了一定程度的超压现象，建议设计时适当考虑超压系数，可取 1.2～1.3[11-12]。

3 结 论

本文通过开展不同高径比、不同偏心率的缩尺筒仓模型装卸料试验，探讨地上输料通道对浅圆仓仓壁和通道受力的影响，并与筒仓标准GB 50077—2017 相关规定进行了对比分析。获得了以下主要研究结论：

1）装料试验结果表明浅圆仓仓壁侧压力测试值与标准GB 50077—2017 预测值在通道高度以上符合较好，而在通道高度范围内的仓壁侧压力测试值明显小于规范预测值，显然通道的存在影响了仓壁底部的静载侧压力分布。

2）整个卸料过程可以归纳为一个倒锥不断下切的过程，倒锥的顶点位于卸料口的正上方。缩尺卸料试验中没有观测到超压系数Cd随着卸料偏心率e/dn增大而增大的现象。高径比hn/dn在0.69 以下时，仓壁和通道上超压系数普遍较小；高径比hn/dn接近1.0 时，仓壁和通道上超压系数Cd迅速上升。在卸料偏心率较小时（e/dn<0.2），缩尺试验超压系数Cd测试值稍大于GB 50077—2017 的预测值；卸料偏心率较大时（e/dn≥0.2），标准GB 50077—2017的预测值基本上偏于安全。

3）浅圆仓主次通道顶壁及侧壁的静载压力依据本文提出浅埋公式计算更加合理，其中贮料高度H应取为通道计算点的实际贮料高度。标准GB 50077—2017 中贮料高度H恒定为贮料计算高度hn，无法反应沿通道轴线贮料高度的变化，更为严重的是通道被判定为深埋时，通道压力预测值明显小于测试值，偏于不安全。

4）主通道顶壁离卸料口稍远距离的通道顶壁呈现明显的超压现象；主通道侧壁的超压现象在卸料口附近最为严重；次通道顶壁和右侧壁超压现象基本可以忽略；次通道左侧壁因直接面对卸料口，出现明显超压现象。建议设计时适当考虑通道的顶壁和侧壁超压系数，可取1.2～1.3。