基于D-H 法的果园作业平台工作空间分析与试验
2020-10-21樊桂菊牛成强
李 钊,樊桂菊 ,梁 昭,牛成强
(1. 山东农业大学机械与电子工程学院,泰安,271018;2. 山东省园艺机械与装备重点实验室,泰安,271018;3. 山东省农业装备智能化工程实验室,泰安,271018)
0 引 言
中国果园种植面积和水果产量居世界首位,但水果产业属于劳动密集型产业,尤其剪枝、疏花疏果、采摘等环节人工劳动强度大、效率低[1-3]。近年来,由于农村劳动力的转移和人工成本的提高,辅助人工作业的果园平台的研究与应用越来越多[4-6],但主要集中在结构与功能方面,对其运动学与工作空间的研究比较少。随着现代化果园种植面积的扩大和人们对农业机械性能要求的提高,农机农艺有机融合成为研究的重点和难点,果园作业平台工作空间代表了其活动范围,反映了平台与果树种植模式的融合程度,直接影响作业人员的工作舒适度,是其运动灵活性的重要衡量指标[7-8]。因此对果园作业平台进行运动学与空间分析具有重要的意义。
许多学者开展了农业机械或农业机器人运动学与工作空间分析方面的研究。胡建平等[9]采用几何法分析其约束方程及边界方程求解了Delta并联机构移栽机器人可达工作空间,并以机器尺寸及运动学性能为综合进行优化;李国利等[10]采用D-H 法建立了苹果采摘机械手正运动学方程,通过蒙特卡洛方法模拟了机械手工作空间;吴超宇等[11]提出了极坐标变步长迭代搜索法分析了并联机器人的工作空间,以对空间利用率最大为目标进行了参数优化;阳涵疆等[12]基于旋量理论构建了一种混联采摘机器人运动学方程;权龙哲等[13]采用D-H 法建立了立体苗盘管理机器人运动学模型,通过几何图解法得到了工作空间及约束关系,进而优化机械臂参数。
综上所述,目前分析机构的工作空间主要有几何法、解析法和蒙特卡洛方法,几何法和解析法仅适用于自由度或杆件数目较少的机构工作空间分析[14-15];蒙特卡洛方法算法比较简单,适用范围广泛,但边界提取精度依赖于边界点分布状况,模拟点多出现在非边界处,造成点浪费且边界不清等[16]。
针对以上问题,本文在前期研制的果园作业平台基础上,通过D-H 法建立坐标系,推导其运动学模型,采用U形反正弦分布函数对蒙特卡洛方法改进,利用MATALB 得到参考点工作空间点云图,采用网格化算法分析改进前后的工作空间边界清晰度,并通过仿真及样机试验进行验证,为原型结构参数优化和智能控制提供理论依据。
1 果园作业平台结构
1.1 结构简介
果园作业平台整体结构包括动力装置、行走机构、回转机构、升降机构、调平机构、工作台和控制系统等[17],辅助人工完成剪枝、疏花疏果、套袋及果实采摘等环节。为适应果园复杂地形,采用履带式底盘,其工作原理为:回转机构使工作台在果树行间左右摆动;升降机构通过油缸伸缩带动工作台上升或下降,满足果树不同高度的操作要求;调平机构主要由调平油缸、调平液压回路和调平控制系统组成,通过电磁阀控制调平油缸伸缩改变工作台横坡和纵坡倾角,实现平台坡地作业时工作台保持水平。因此,该平台既适用于乔砧密植的纺锤形平地果园,也适用于坡度为15°以内的山区果园。
根据上述结构和工作原理,果园作业平台的一系列动作与串联机器人相似,回转机构相当于回转关节,升降机构相对于立柱的运动构成旋转关节,工作台的横坡调平运动和纵坡调平运动分别构成 2 个旋转关节,因此该平台可看作串联开链机构。为便于作业平台运动学模型求解、工作空间分析和试验验证,以纵坡调平油缸和工作台的连接点作为作业平台执行端参考点,简称平台参考点。
1.2 自由度计算
机构自由度计算公式[18-19]为
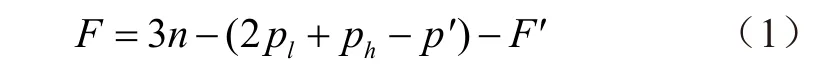
式中F表示机构自由度,n表示零件个数,pl表示平面低副,ph表示平面高副,p'表示虚约束,F'表示局部自由度。
由果园作业平台结构和工作原理可知,其构件个数n为 11,将履带式底盘看作移动副,则该平台的平面低副pl=14(转动副10 个、移动副4 个),平面高副ph=0,虚约束p’=0,局部自由度F’=0,将以上数据代入式(1),得果园作业平台的自由度为5。
1.3 果园作业平台运动学模型
1.3.1 基于D-H 法建立坐标系
D-H 法[20-23]通过α、ɑ、d、θ4 个独立参数描述相邻杆件之间的坐标方向和参数,可以有效的确定开链式串联机器人手臂关节参数和关节变量。
为描述果园作业平台工作台的运动,对其作如下假设:地面为刚性,各构件为刚体,各油缸质量忽略不计,忽略铰链间隙与摩擦力的影响。根据假设,立柱支承的上铰接点至底盘为连杆1,立柱为连杆2,两立柱支承连线中点至立柱为连杆3,横梁为连杆4,工作台与横梁、纵坡调平油缸铰接点间的杆为连杆5。以立柱到地面的投影为初始坐标系原点O0,如图1 采用D-H 法建立果园作业平台连杆坐标系,相应的D-H 参数如表1 所示。
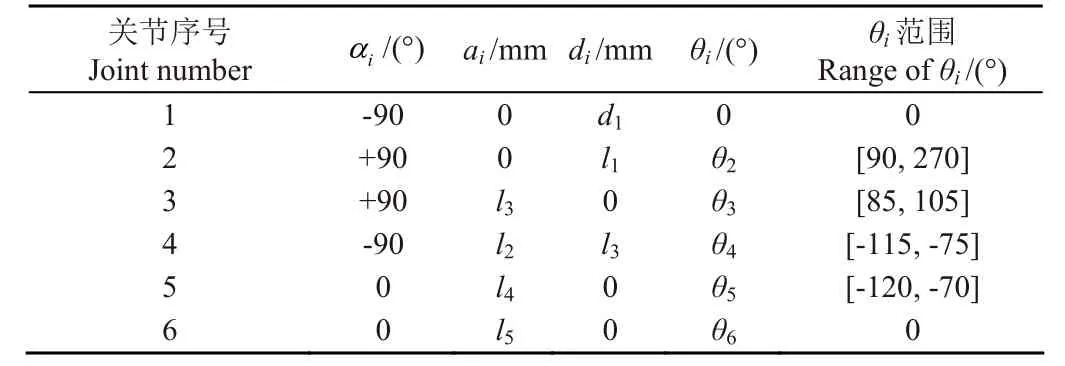
表1 果园作业平台D-H 参数Table 1 D-H parameter of orchard platform
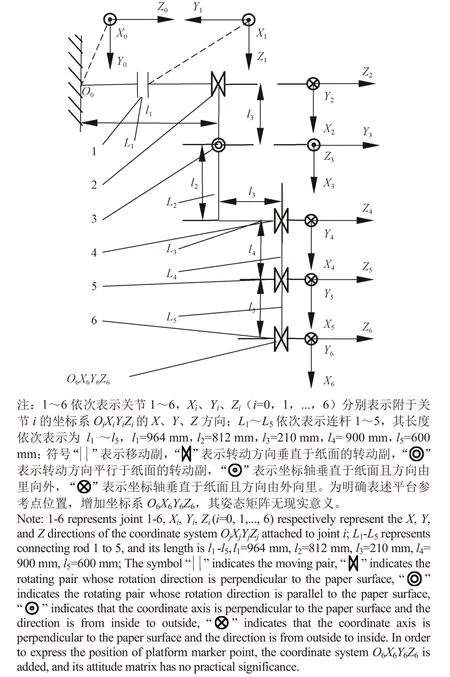
图1 果园作业平台坐标系Fig.1 Coordinate system of orchard platform
1.3.2 正运动学方程
相邻两坐标系i和i-1 之间的位姿变换矩阵Tii-1[24-26]为
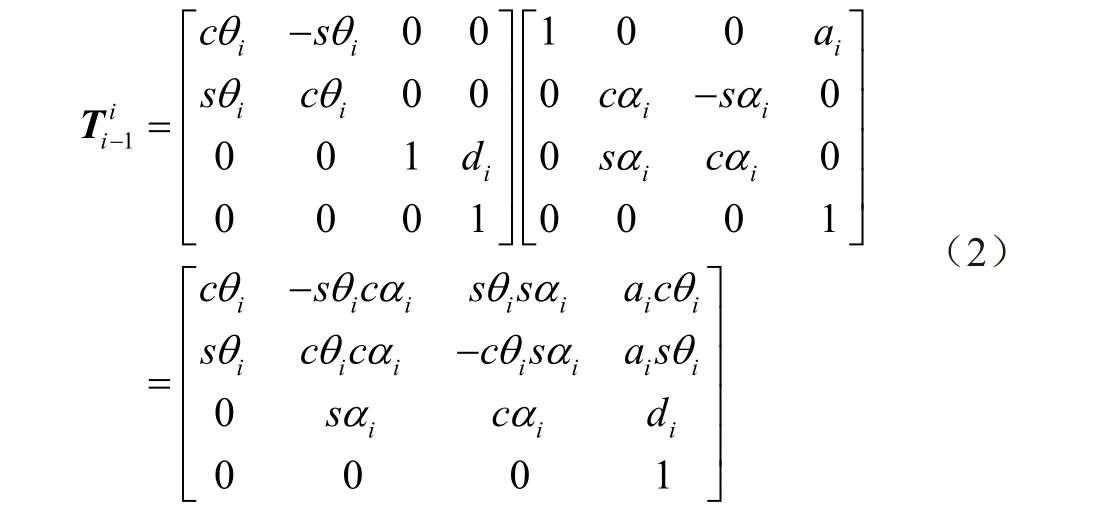
式中cθi=cosθi,sθi=sinθi,c iα=cosiα,s iα=siniα,i=1,2 ...6,下同。
平台参考点的正运动学方程为
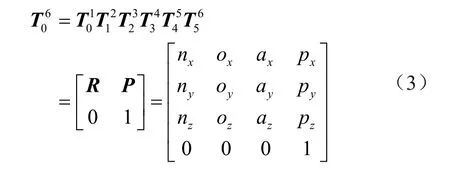
式中R为姿态矩阵,P为位置矩阵,n,o,a,p均为di与θi的函数,具体如下
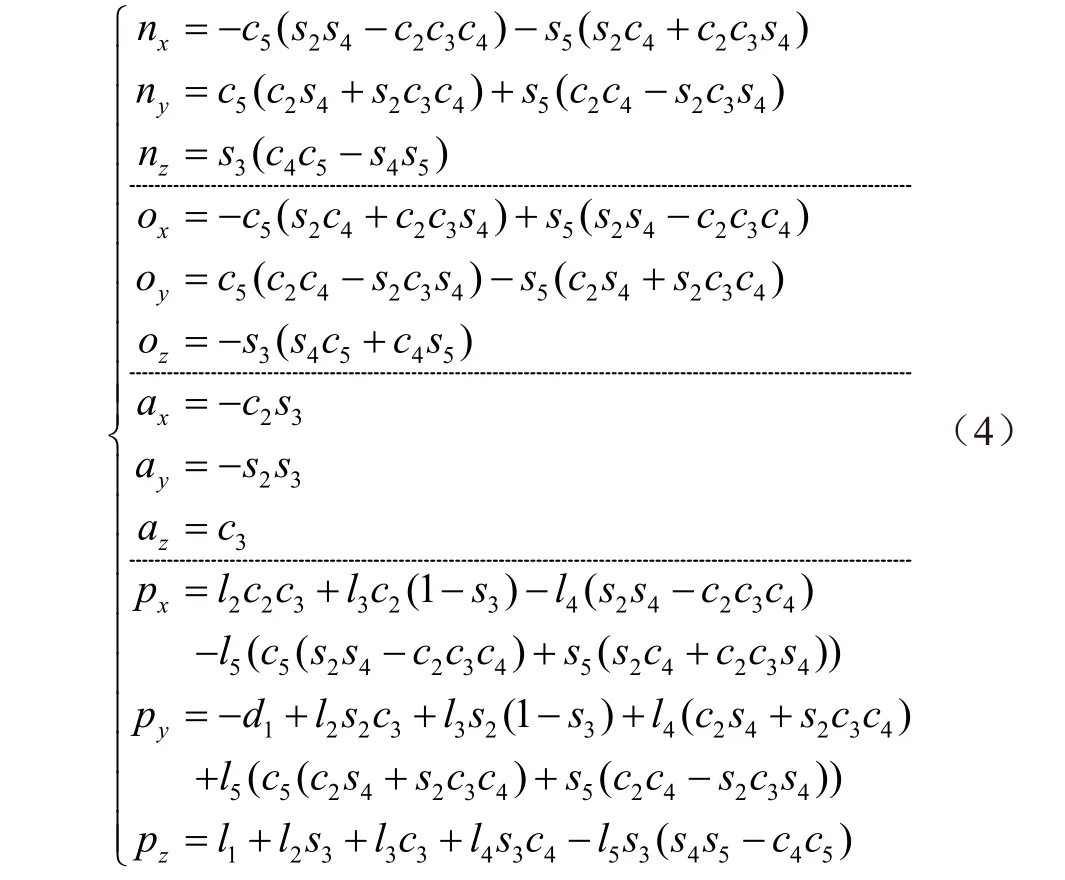
2 工作空间分析
2.1 理想工作空间
果园作业平台的工作空间是指平台参考点所能达到的所有位置空间点集的集合,表示了其工作范围,是作业平台结构设计和优化的重要依据,其理想工作空间与果树种类、种植模式和操作人员自身因素密切相关。中国水果种植种类繁多,其中苹果种植面积位居前列,目前种植模式主要有:乔砧稀植、乔砧密植和矮砧密植[27]。本文以乔砧密植的纺锤形苹果园为研究对象,其株行距为(3~4)m×(4~5)m,株高 2.8~3.5 m,冠径1.4~3.0 m[28]。
综合苹果园种植模式、平台通用性和操作人员自身因素,平台参考点的理想工作空间如图2 所示。
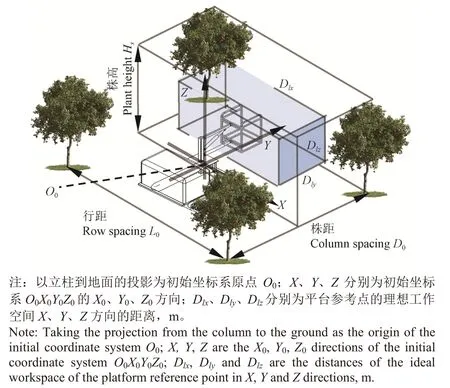
图2 平台参考点理想工作空间示意图Fig.2 Schematic diagram of orchard platform reference point ideal workspace
平台参考点的理想工作空间X、Y、Z三个方向的距离Dlx、Dly、Dlz为

式中Ls为冠径,m;Lr为成人胳膊长度,m;Hr为成人双臂功能上举高,m;Lz为灵活长度,m。
由文献[28],各参数取值为:D0、L0、Hs分别取最大值 4、5、3.5 m,Ls取最小值 1.4 m;由文献[29],Lr= 0.6 m,Hr= 2 m,Lz= 0.1 m。代入式(5)可得Dlx= 2.5 m、Dly=1.5 m、Dlz= 1.6 m,平台参考点理想工作空间大小为2.5 m×1.5 m×1.6 m。
2.2 蒙特卡洛方法改进
蒙特卡洛方法是一种基于大数定理和中心极限定理[30-31]的应用较广的数值法,通过人为构造合理的随机概率模型,在机构关节空间内随机产生关节空间点,利用坐标变换矩阵T逐一映射到工作空间内,得到一定数量的平台参考点位置随机点,将这些点以点云图形式显示,即可直观地描述工作空间情况。
一般采用均匀分布模型R(a,b)产生随机点,其概率密度函数为
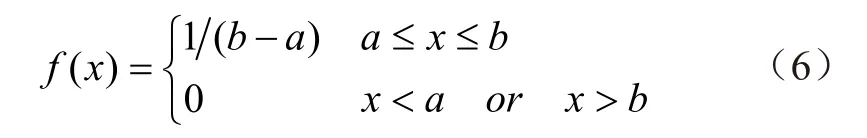
式中a、b表示样本在区间[a,b]服从均匀分布。
因此,果园作业平台关节空间点为
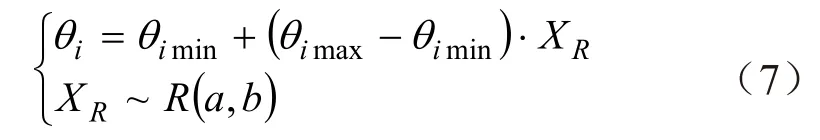
式中θimax与θimin分别为关节角θi的最大值、最小值。本文关节角取值为包括关节角范围内所有值,a=0,b=1,下同。
根据表 1 的作业平台参数,通过蒙特卡洛方法模拟105个点得平台参考点的工作空间位置点云图如图 3a 所示,为更清晰表达工作空间边界处点云分布情况,截取Z>1 500 mm 部分如图3b 所示。
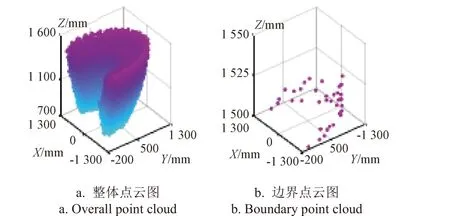
图3 平台参考点工作空间(均匀分布)Fig.3 Platform reference point workspace(uniform distribution)
由图 3 可知,平台参考点的工作空间边界位置点云稀疏,大多数点分布于非边界位置,原因在于:1)关节空间边界取值不理想,模拟105次服从均匀分布R(0,1)的随机数抽样,得到随机数集合,如图4 所示,以[0, 0.01]和[0.99, 1]为边界域,其范围内的分布点占比pbo,由式(8)计算得2.00 %;2)作业平台正运动学方程为非线性方程,将关节空间取值在映射过程中“拉伸”或者“压缩”,导致工作空间边界处点分布较少,非边界部分点分布集中,造成点浪费、边界不清晰。因此需要对蒙特卡洛方法进行改进。
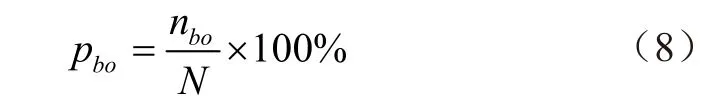
式中nbo表示边界域内分布点个数;N表示总模拟点个数,105个。
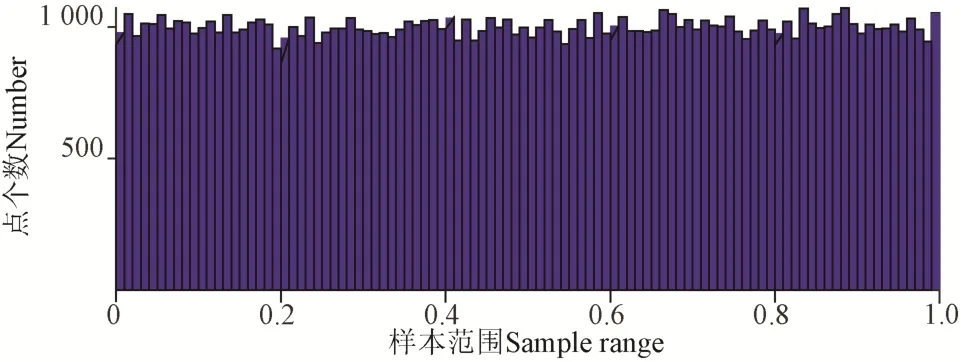
图4 均匀分布的分布模拟Fig.4 Distribution simulation of uniform distribution
根据上述分析,为增加平台参考点工作空间边界分布点,得到清晰的工作空间,关节空间取值分布需要边界处高而中心处低,故采用U 形的反正弦分布,其概率密度函数为
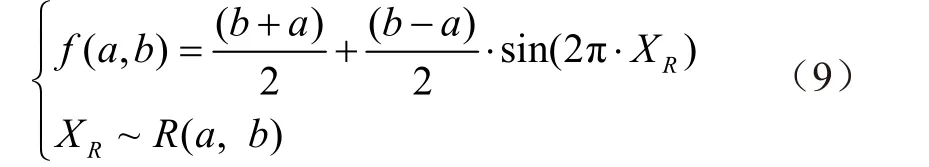
模拟105次服从该分布的随机数抽样,如图5 所示,该随机数边界处分布点数明显增多,以[0, 0.01]和[0.99, 1]为边界域,由式(8)计算得其范围内的分布点占比为12.76%,较均匀分布提高了10.76 %。
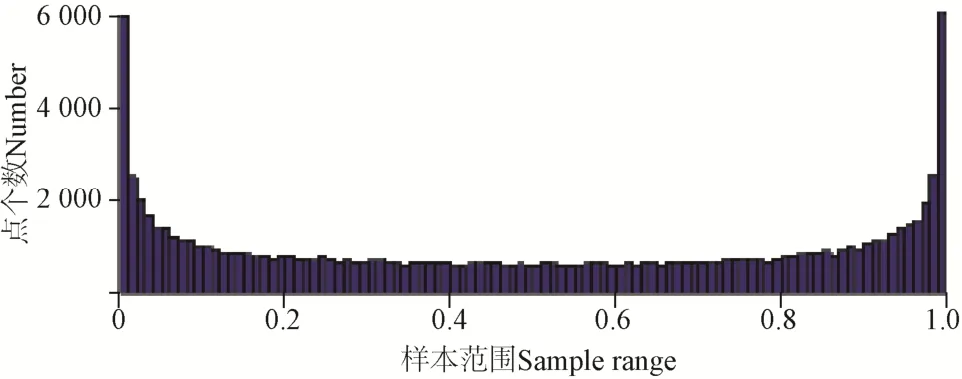
图5 反正弦分布的分布模拟Fig.5 Distribution simulation of arcsine distribution
采用改进蒙特卡洛方法得作业平台参考点的工作空间位置点云图如图6,可知其工作空间边界部分点分布增加,边界线明显清晰。
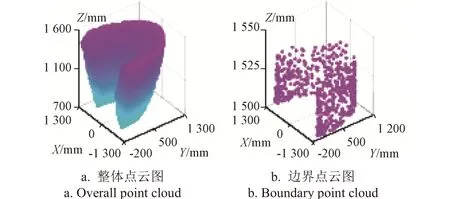
图6 平台参考点工作空间(反正弦分布)Fig.6 Platform reference point workspace(arcsine distribution)
2.3 网格化算法
为进一步量化改进后的工作空间边界清晰度,采用网格化算法[32]分别对改进前后的工作空间点云图进行分析,具体如下:
1)外包长方体设计:根据工作空间点云图得到平台参考点在三维方向的最值,以略大于这些最值设计外包长方体,使得工作空间的所有点都分布在该长方体内。设该长方体在3 个坐标轴方向上的最值分别为xmin、ymin、zmin、xmax、ymax、zmax,则长方体表示为
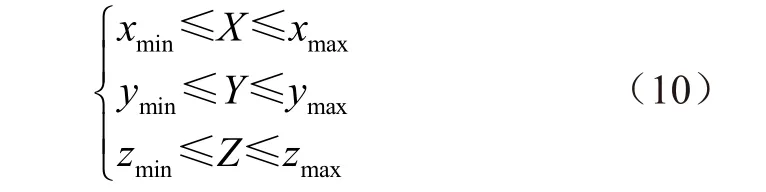
2)工作空间网格化:将上述长方体沿3 个坐标轴方向按照2Δ的步长间隔,划分为若干个小立方体,定义为网格化子空间,如图 7 所示。假设某个子空间中心坐标为(x0,y0,z0),则子空间顶点坐标为(x0±Δ,y0±Δ,z0±Δ)。
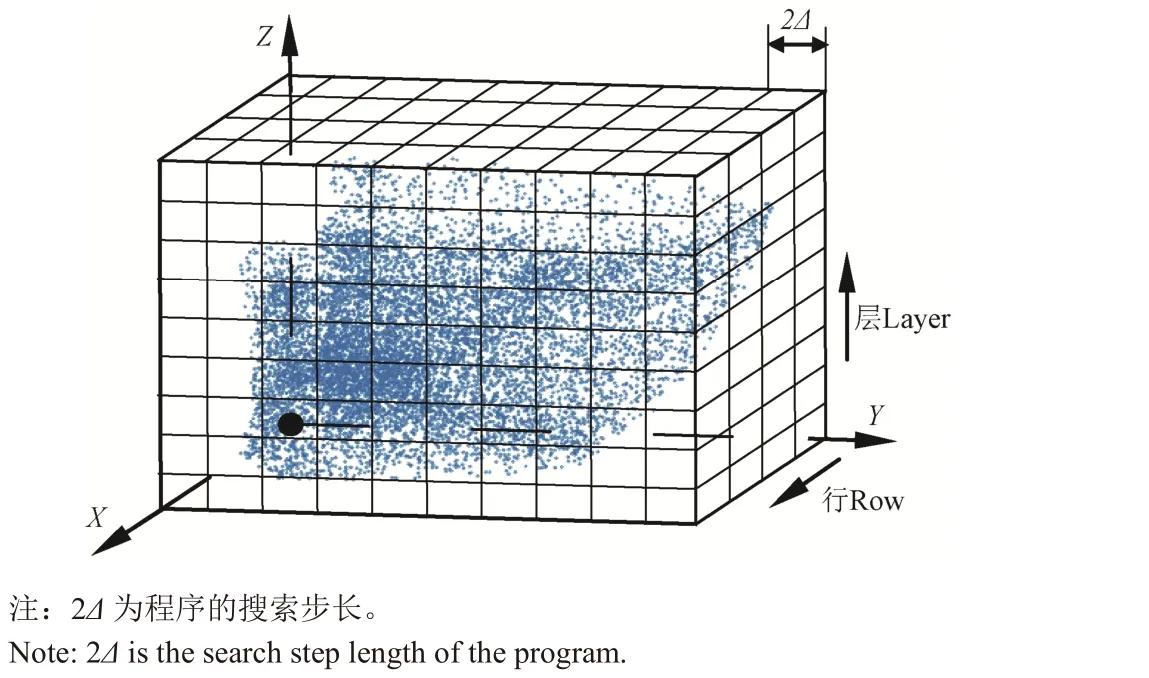
图7 网格化空间示意图Fig.7 Schematic diagram of gridded space
3)子空间有序化:基于网格化子空间,沿Z方向按步长2Δ划分为若干层,然后沿Y方向按步长2Δ划分为若干行,以“层-行”编号将子空间有序化处理。
4)子空间初筛:为节约计算时间,按“层-行”搜索所有子空间,初步筛除内部不含点的子空间,保留内部含有点的子空间。
5)边界子空间搜索:对于保留的子空间,仍然按照“层-行”的逻辑搜索,若子空间连续,则每一行的最大值及最小值所在的子空间为边界子空间;若子空间不连续,则空间内有点而相邻子空间无点的子空间为边界子空间。
6)清晰度评价指标:以边界分布点总个数和最底层和最顶层边界层面积为衡量清晰度的评价指标。其中边界分布点总个数指所有边界子空间的包含点数总和,边界层面积指第i层边界点封闭拟合曲线的面积,可分别用式(11)和式(12)表示。
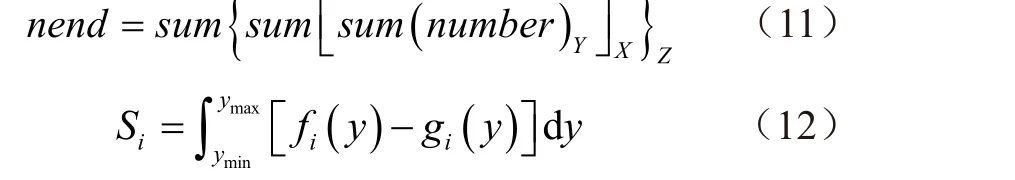
式中nend为边界分布点总个数;fi(y)、gi(y)为第i层边界点在XOY平面投影的拟合曲线(4 次多项式拟合);Si为该封闭拟合曲线的面积,m2;ymin与ymax分别为外包长方体在Y轴的最大值、最小值,mm。
根据算法分析改进前后的平台参考点工作空间,考虑程序运行速度与计算精度,步长2Δ取10 mm,模拟点105个时边界分布点总个数分别为 2.85×104和 3.53×104;将改进前后的工作空间在同一边界层投影如图8,根据式(12)计算,改进前后最底层和最顶层边界层面积分别为0.057、0.16 和0.11、0.22 m2。由此可知改进后工作空间边界分布点个数提高23.74 %,最底层和最顶层的边界层面积增大180.70 %和102.69 %,表明改进后工作空间边界清晰度提高,网格化算法有效。
2.4 可达工作空间
根据蒙特卡洛方法原理,通过该方法得到工作空间的解是平台参考点到达位置的统计参量,是实际位置的近似值,为更加逼近平台参考点实际位置,采用 2 种方法多次生成工作空间,取其工作空间X、Y、Z方向的平均值,记为平台参考点的可达工作空间,即
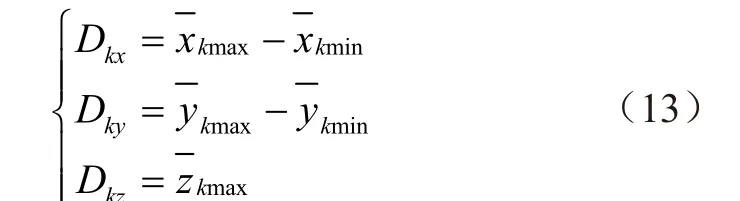
式中Dkx、Dky、Dkz为平台参考点可达工作空间在X、Y、Z方向的距离,mm;与分别为工作空间点云在X、Y和Z方向取10 次最大值、最小值的平均值,mm。
以105个点模拟出平台参考点的工作空间位置点,分别采用2 种方法进行10 次,得其3 个方向的坐标最值如表 2 所示,引入空间差异系数r描述可达工作空间与理想工作空间的误差。
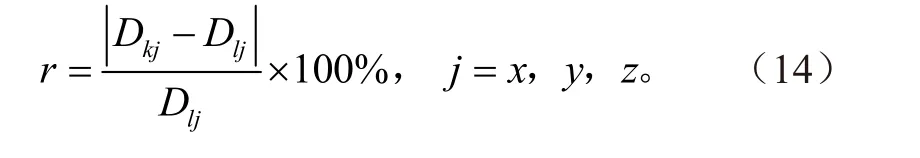
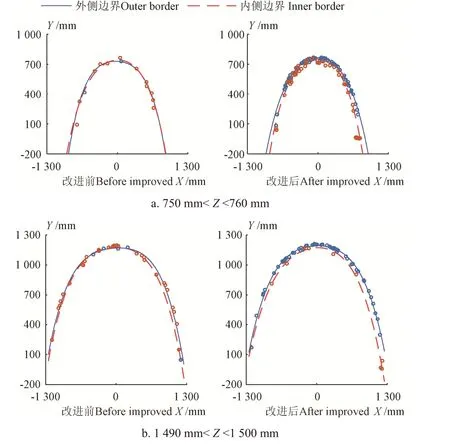
图8 边界拟合曲线Fig.8 Boundary fit curve
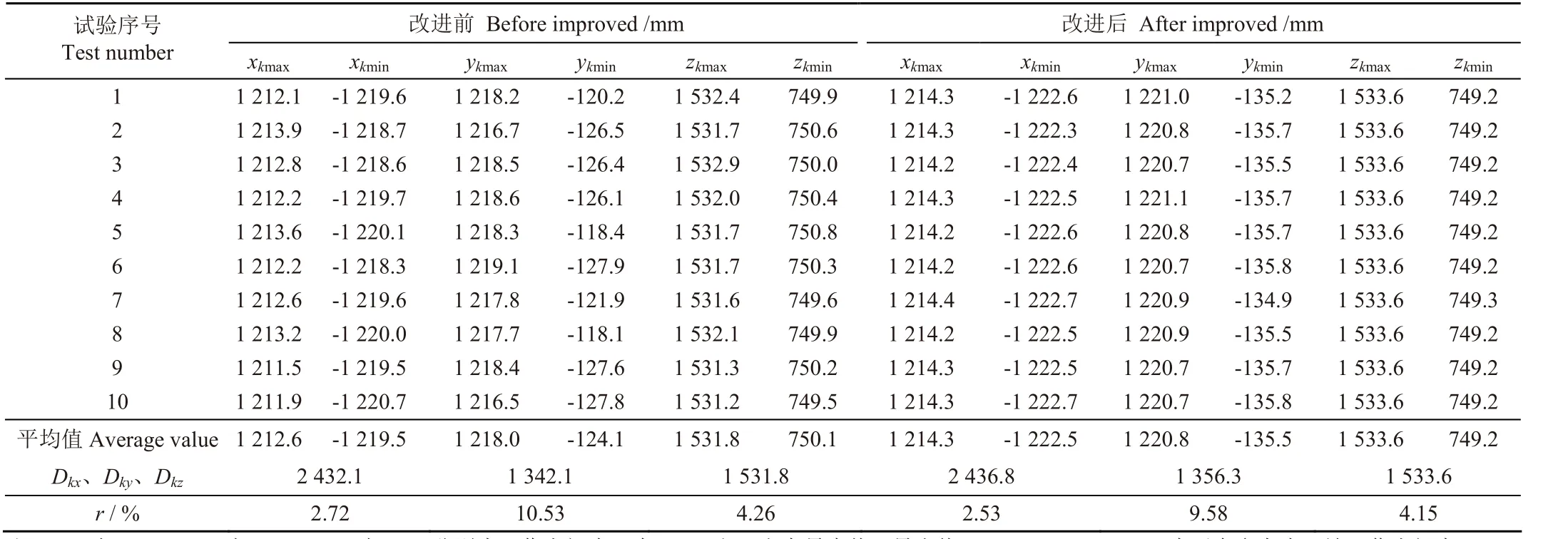
表2 平台参考点工作空间坐标最值Table 2 The minimum and the maximum of platform reference point workspace
根据表 2 数据和平台参考点的理想工作空间计算空间差异系数,改进后平台参考点X、Y、Z三个方向的空间差异系数分别为2.53 %、9.58 %、4.15 %,较改进前分别降低了6.92 %、8.99 %、2.64 %,表明改进后生成的工作空间更接近理想工作空间。
3 样机试验
3.1 试验设备
基于前期研制的果园作业平台,进行其运动位置跟踪与工作空间分析试验。平台以柴油机为动力源,主要参数如表3 所示。
试验采用北京约克科技有限公司的VEO410L型高速摄像机(拍摄分辨率 1 280×720,帧率 1 000 帧/s,曝光时间40μs)跟踪平台参考点位置;采用上海直川电子科技有限公司的ZCT230M 倾角仪(精度0.05°,数据通过RS485 连续输出)测量油缸旋转角;采用日本Panasonic公司 HG-C1100 激光位移传感器测量油缸位移量,精度0.01 mm;此外,还包括余姚索普电子科技有限公司的VC-400HSS 高速摄影灯(400 Ws)、杰科斯JK-100F 系列土壤水分仪(分辨率0.1 %)、卷尺、秒表等。

表3 果园作业平台主要技术参数Table 3 Main parameters of orchard platform
3.2 试验内容及方法
3.2.1 平台参考点位置跟踪试验
根据《农业机械生产试验方法》(GB/T 5667—2008)[33]进行平台参考点位置跟踪试验,验证平台运动学模型的准确性。由于果园地形复杂和种植模式限制,高速相机不能很好捕捉平台参考点完整运动,因此在山东农业大学农学实验站空旷硬质地面上进行试验,如图 9 所示为位置跟踪试验现场,试验时间为2019 年10 月。

图9 位置跟踪试验现场Fig.9 Position tracking test site
因样机液压回路不能实现多个油缸同时稳定给油,将回转支承和横坡调平油缸保持中位,纵坡调平油缸缩短至最小位移,升降油缸由最小行程伸长到最大行程的过程中,通过倾角仪实时测量横梁旋转角(θ4)和横梁与工作台之间旋转角(θ5),利用高速摄像机跟踪平台参考点,拍摄过程共5 681 帧,以间隔1 136 帧截取图像,如图10 所示。

图10 高速摄像图像Fig.10 High-speed camera image
3.2.2 平台参考点工作空间试验
为获得平台参考点在实际果园的工作空间,2020 年6 月在山东农业大学园艺实验基地果园进行现场试验。该果园主要种植苹果树,乔砧密植,树龄 8a,树形为自由纺锤形,株行距为2 m×3 m,平均株高为3.5 m,平均冠径为2.4 m。试验时环境温度为32 ℃,园地内地形较为平整,浅层土壤含水率约为18.7 %。
以D-H 坐标原点为实际坐标原点,调整回转支承和各油缸状态,分别测量平台参考点实际工作空间在X、Y、Z三个方向所能达到的最大值、最小值,如图 11 所示。

图11 平台参考点工作空间极限位置Fig.11 Limit position of platform reference point workspace
3.3 试验结果与分析
3.3.1 平台参考点位置分析
根据高速摄像机得到的平台参考点运动跟踪图像和倾角仪测得的角度,得到图10 中对应各帧图像中的平台参考点Y和Z方向坐标值和相应的关节角θ4与θ5,因回转支承和横坡调平油缸保持中位,故平台参考点在X方向上无变化。由样机参数和试验条件确定d1=0 mm、θ2=90°、θ3=90°,代入运动学模型得平台参考点Y和Z方向的计算值,如表4。
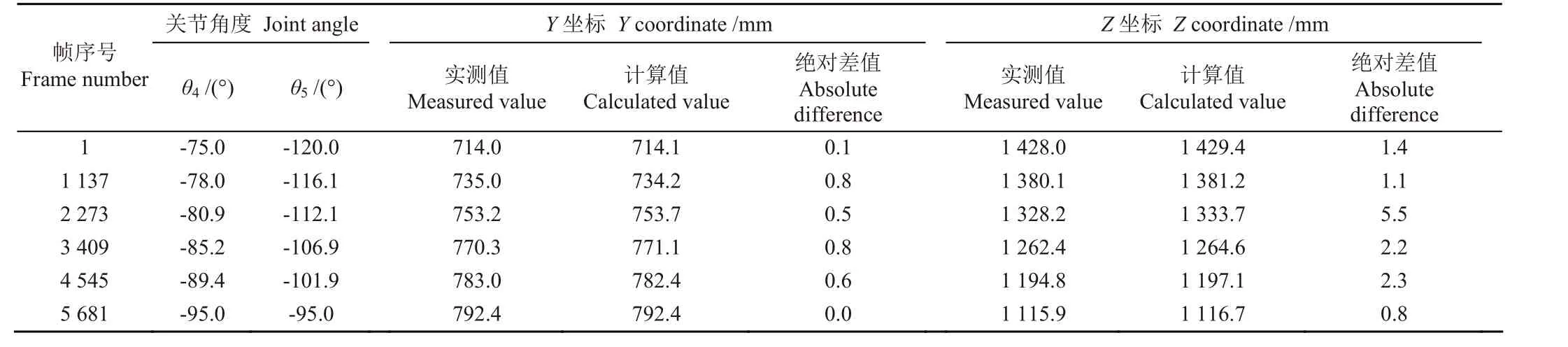
表4 各帧对应的平台参考点Y 和Z 方向坐标实测值与计算值Table 4 Measured and calculated values of Y and Z coordinates of platform reference points corresponding to each frame
由表4 可知,所选帧对应的Y方向和Z方向的最大差值分别为0.8 和5.5 mm。
为描述升降油缸整个伸长过程平台参考点的运动,利用Tema 软件导出拍摄图像的平台参考点位置数据,以改进后蒙特卡洛方法求得的运动学正解为对照组,采用MATLAB 绘制平台参考点运动轨迹,如图12 所示。
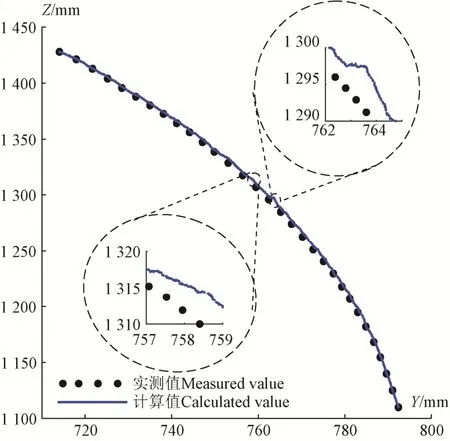
图12 平台参考点实测值与计算值轨迹Fig.12 Measured value and calculated value track of platform reference point
由图12 可知,平台参考点的实测值与计算值基本吻合,当Z为1314.4 mm 时,Y值差值最大为1.2 mm;当Y为763.6 mm 时,Z值差值最大为6.2 mm,表明运动学模型和求解方法正确。
3.3.2 平台参考点实际工作空间分析
平台参考点实际工作空间为
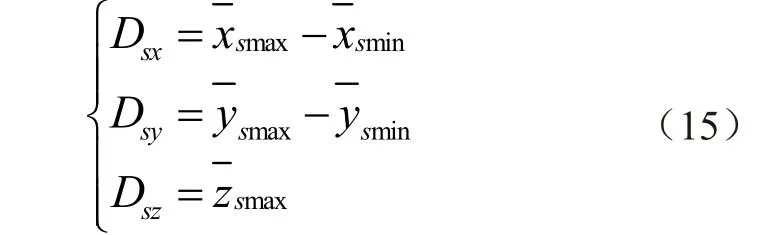
式中Dsx、Dsy、Dsz为平台参考点实际工作空间在X、Y、Z三个方向距离,mm;与分别为实际工作空间在X方向、Y方向和Z方向取10 次最大值、最小值的平均值,mm。
调整回转支承和各油缸状态进行10 次试验,测量平台参考点实际工作空间在X、Y、Z三个方向的最大值、最小值,并求取最大值、最小值的平均值代入式(15),得:Dsx=2 430.2 mm、Dsy=1 346.0 mm、Dsz=1 533.7 mm。
利用空间差异系数r′=( |Dsj-Dlj| /Dlj)×100%(j=x、y、z,下同)和r″=( |Dsj-Dkj| /Dkj)×100%分别描述实际工作空间与理想工作空间和可达工作空间的误差,则平台参考点实际工作空间与理想工作空间和可达工作空间的对比如表5 所示。
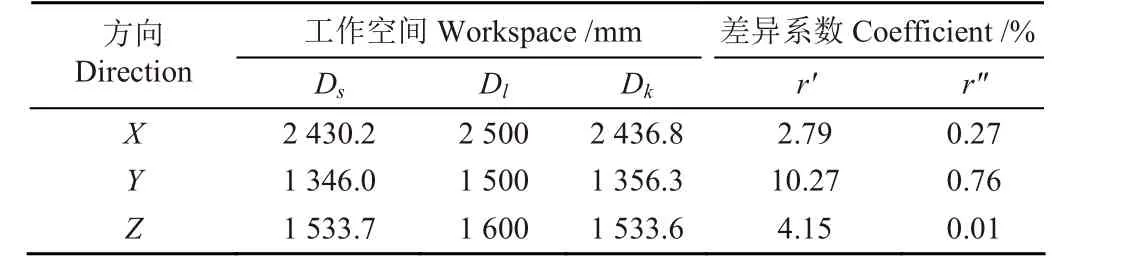
表5 实际工作空间与理想工作空间和可达工作空间对比Table 5 Actual workspace compared with ideal workspace and reachable workspace
由表 5 可知,平台参考点实际工作空间与理想工作空间差异较大,Y方向最大,达到10.27 %,主要原因在于设计样机时侧重行距和株高,株距考虑的较少,但因Y方向为前进方向,对实际作业影响不大;与可达工作空间的差异较小,X、Y、Z三个方向的空间差异系数r″分别为0.27 %、0.76 %和0.01 %,表明通过改进的蒙特卡洛方法分析工作空间有效。
另外试验过程中,偶尔会出现运动不连续、参考点出现晃动等现象,分析原因主要有:安装铰链存在间隙和摩擦;升降速度过快,作业平台由于惯性产生摆动。
4 结 论
1)本文以前期研制的果园作业平台为研究对象,以简化的作业平台模型建立D-H 坐标系,推导了果园作业平台平台参考点的正向运动学方程。
2)利用U 形反正弦分布函数改进了蒙特卡洛方法,采用网格化算法对改进前后生成的工作空间进行分析,改进后最底层与最顶层边界面积分别增大 180.70 %和102.69 %,与理想工作空间X、Y、Z三个方向的差异系数较改进前分别降低了6.92 %、8.99 %、2.64 %,表明改进后工作空间边界清晰度明显提高,更接近理想工作空间。
3)对平台进行位置跟踪和实际空间测试:平台参考点位置的实测值与计算值基本吻合,最大差值仅为6.2 mm,表明运动学模型正确;平台参考点实际工作空间与理想工作空间差异较大,而与可达工作空间差异较小,与可达工作空间差异系数最大仅为0.76 %,表明改进方法有效,为下一步作业平台结构和参数优化提供理论基础。
