高三数学概念复习教学的实践思考
2020-10-20王爱斌
王爱斌
[摘 要] 弱化概念教学的现象在高三数学复习教学中普遍存在,这对于高三数学复习的有效性会产生巨大的负面影响,教师应从回归知识本源、反思学习过程、立足通性通法、渗透数学思想方法等多方面进行数学概念的复习教学,引导学生充分感受数学的内涵并因此帮助学生树立一种精神,养成一种气质,深植一份思想内涵.
[关键词] 复习教学;概念教学;知识本源;反思;通性通法;数学思想方法
从解题教学层面谈高三复习教学有效性的观点颇多,笔者结合自己的教学与体会主要从概念课的复习进行思考. 数学概念这一揭示现实世界空间关系与数量关系的思维形式实际上就是客观事物中数与形的本质属性的反映. 与此同时,这一数学学科的灵魂与精髓也是导出数学定理与法则的逻辑基础.
不能围绕数学概念核心进行的教学往往会使学生盲目进行大量的解题操练,导致教学缺乏必要根基的同时也令广大学生的数学基础相对薄弱.事实上,高三数学复习教学也因为“题海战术”的影响而存在弱化概念教学的现象,主要表现为:
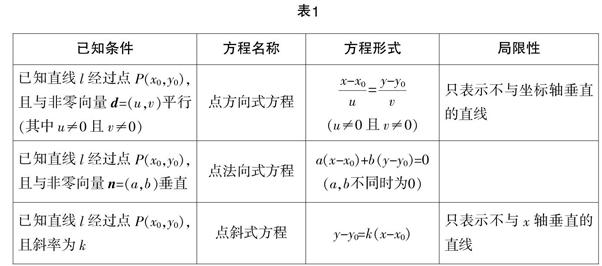
1. 存在让学生自主复习概念的教学行为. 这是受“先学后教”这一教学策略影响而形成的. 比如,有的教师在直线的方程这一内容的教学中往往会设计以下表格并请学生自主填写(表1).
2. 存在定义、性质、公式直接告知或共同回忆的行为.比如,有的教师在复习“解斜三角形”这一内容中往往会先要求学生回忆三角形内角和、面积公式、正弦定理、余弦定理等概念或公式,然后进行针对性的反复练习,对于定理的证明却往往视而不见.
3. 存在就题论题的教学行为. 有的教师因为集体备课、统一习题的原因往往会在例题讲评时形成就题论题的教学行为,例题背后隐藏的概念却往往得不到应有的挖掘. 很多教师在试卷讲评课上顺着题目序号一一讲解的现象比比皆是,对于为何如此解题往往置之不理,知识拓展与提升严重缺乏的同时也令学习的效益大大降低.
4. 存在不揭示概念实质的教学行为. 有的教师虽然在教学中能够关注数学思想方法的渗透,但对其实质却往往不能进行很好的揭示.
例:过点P(1,2)作直线l与x轴、y轴的正半轴分别交于A,B两点,则PA·PB的最小值是多少?此时直线l的方程如何?
此题的解法多样:(1)设斜率,求得交点之后再运用基本不等式进行解题;(2)设斜率,求得交点之后再运用构造平行向量工具进行解题;(3)设∠BAO=α并借助三角函数的有界性进行解题.解法众多,但很多教师对于此题为何能进行“一题多解”却往往不做解释.再比如,求y=■的最值一题,很多教师对于此题为何能运用“数形结合”方法解题往往也不做解释.
这些现象的产生基本都是因为教师对概念教学的认知不足而造成的,很多教师因为高一、高二对概念已经进行过教学而在复习教学中不再重视. 但实际上,学生对概念不清的实际学习状况往往会造成其复习的低质低效.如何改变这一局面呢?
回归知识本源
搞清基本概念、原理、方法的复习教学能使学生对知识本质产生理解和感悟并构建起知识间的联系,使学生不断完善知识的结构并令知识体系的功能得到强化.
例:已知f(x)为定义在[-1,1]上的奇函数,且f(1)=1,若m,n∈[-1,1],且当m+n≠0时恒有■>0成立. (1)用定义证明f(x)在[-1,1]上为增函数;(2)解不等式fx+■ 此题涉及函数单调性的复习以及函数单调概念中的某些内在关系,比如假设,①任取x1 教师在概念复习中应突出其过程与对象的双重性并体现其现实背景与寓意,使学生能够在概念的形成、发展与应用过程中获得认知结构的完善与思维能力的发展. 反思、优化学习过程 引导学生在概念复习中进行已有知识基础上的反思能使其不断获得新的知识经验并令学习过程得以优化.比如,教师在“解斜三角形”的复习教学中可以引导学生进行以下问题的思考:(1)直角三角形中的边角关系如何?(2)正弦定理从直角三角形中可以提炼出来吗?(3)正余弦定理的证明过程是怎样的?(4)余弦定理和向量的数量积存在怎样的关系呢?(可以将余弦定理的变形公式cosA=■看成为数量积的另一种表达形式b·c=bc·cosA=■的特殊情形) 这种优化学习过程的教学方式能使学生熟练掌握知识的同时弄清知识的形成与发展,使学生能够在概念的现实原型、抽象过程、形式表达、符号化运用等多个层面对概念形成理解与掌握. 立足通性通法 引导学生立足通性通法进行概念内涵与外延的理解与掌握,能使学生更好地抓住问题的本质并因此获得更加完善、稳固的知识结构. 比如,有学生会在判别式的二阶行列式的复习中提出用“D=0,Dx≠Dy”判别线性方程无解,教师应基于学生的这一认知与错误进行概念的复习:用行列式解二元一次方程组,满足D=0且无解,首先应确定Dx或Dy中的一个为具体的非零值,另一个则包含字母,如x+ay=1,x+ay=2,Dx=1 a2 a=-a,Dy=1 11 2=1,则令a=-1即可举出反例. 很多资料对函数值域这一高中重要的数学问题进行了方法的总结,学生在配方法、分离法、换元法、逆求法等众多方法中往往感觉零乱,教师应帮助学生抓住问题的本质及其中所渗透的思想方法并形成科学的学习方法. 渗透数学思想方法 数学思想这一对数学对象的本质认识,实际上是主体在数学认知过程中所提炼的基本观点与根本想法. 例如,求y=■的最值.教师直接选择数形结合的方法来解决此题必然会造成学生心头的疑惑:“我怎会想不出来呢?”因此,在此题的解题教学中,教师可以做如下改进:首先运用万能公式化归成含有“tan■”的函数并启发学生思考,引导学生对繁杂过程中的题目结构进行观察和分析并运用变换主元的办法由正余弦的有界性求解,引导学生从结构中隐藏的点坐标(cosx,sinx)联想到圆并采取构造斜率的方法来解题.数形结合方法在此时出现也就符合学生的思维发展了,学生也因此得到认知的深化与理解并对概念形成更好的掌握.同样的,“过点P(1,2)作直线l与x轴、y轴的正半轴分别相交于点A和点B,求PA·PB的最小值及此时直线l的方程”一题中,教师引导学生对不同点坐标形式展开思考和选择,也会得到不同的解题办法. 教师在复习教学中还应尽量引导学生进行一题多解、一题多联、一题多变,使学生能够在崭新的习题情境中学会更加敏锐地捕捉隐含信息并获得更多的解题感悟.当然,学生在数学学习中的犯错并不止在概念、公式、定理的理解不清上,还有一些非智力因素也会导致其学习出错,教师应及时发现学生的错误并对其出错原因进行分析,使学生能够清晰面对自己的计算错误、策略错误并及时获得正确而简捷的解法. 将知识简单地教给学生在高三数学复习教学中显然是不合时宜的,教师对知识的理解方式并不一定为学生很好地接受,因此,教师在复习教学中仍旧应该重视概念教学并注重学生思维的启发,切忌将自己的直接操作来代替学生的思维,应该引导学生充分感受、理解、领悟数学的内涵并因此帮助学生树立一种精神,养成一种气质,深植一份思想内涵,使学生在充分感受数学课堂的厚重感与力量感的同时建立数学学习的信心,在长才干、长智慧的数学学习中获得数学思维能力与综合素养的锻炼和发展.
