反演点连线垂线的包络图像
2020-10-20田朋朋朱一心
田朋朋 朱一心
(首都师范大学数学科学学院,北京 100048)
0 引 言
柯朗和罗宾[1]介绍了直线与圆的反演的4个性质并给出了初等几何证明.柯熙[2]研究了以圆锥曲线的焦点为反演中心时椭圆、双曲线和抛物线的反演像均为帕斯卡蜗线.本研究在原像与反演像的连线端点处作一垂线,当反演点取遍整个圆锥曲线时,此垂线包络形成的图像.首先利用GeoGebra软件画出了分别以圆锥曲线的焦点、中心和顶点为反演中心时,反演点连线垂线的包络图像,得到定理1~3.利用定理1给出一种轨迹法画圆锥曲线的统一方法,得到定理4.最后结合定理4给出圆锥曲线的包络形成法.得到定理5,并解析证明.本文所述几何图形均指欧氏的平面几何图形.
1 反演点连线垂线的包络图像
圆反演的定义是常见的,例如参考文献[1].
定义1[1]在一确定的平面上,给定以O为中心(称为反演中心),以R为半径的圆C.点C′位于直线OP上,且使得OP·OP′=R2,则点P和点P′互为关于给定圆C的反演点.P到P′的变换叫做反演变换.其中圆C称为反演基圆(图1).
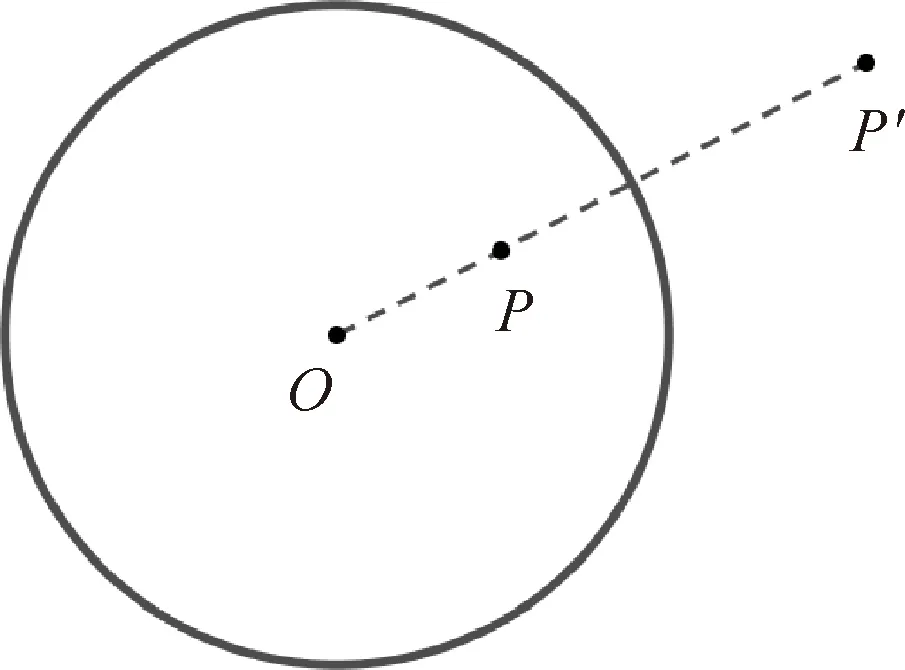
图1 反演基圆
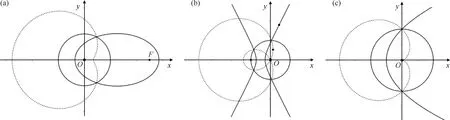
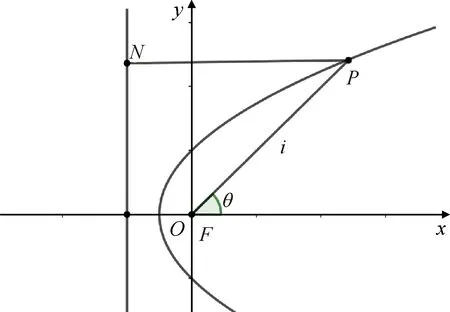
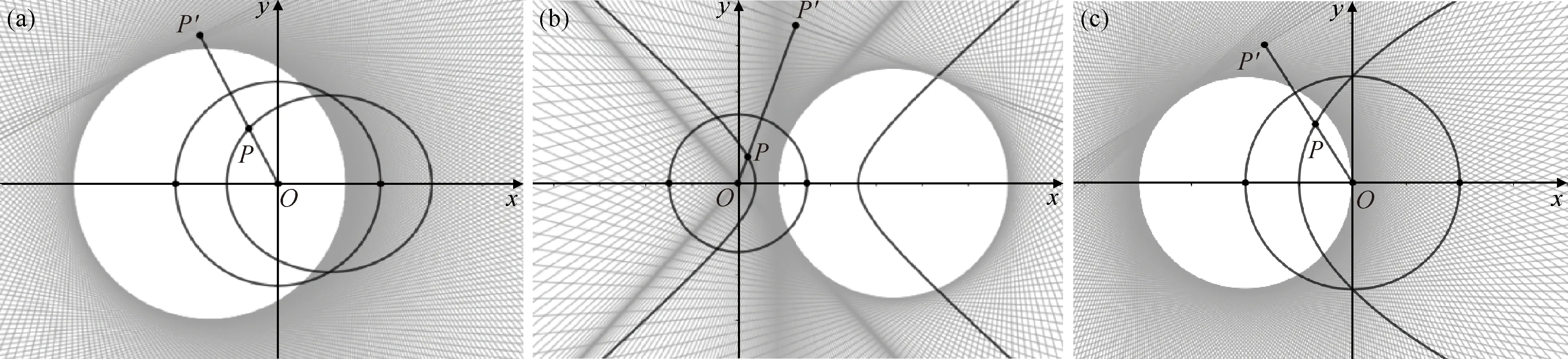
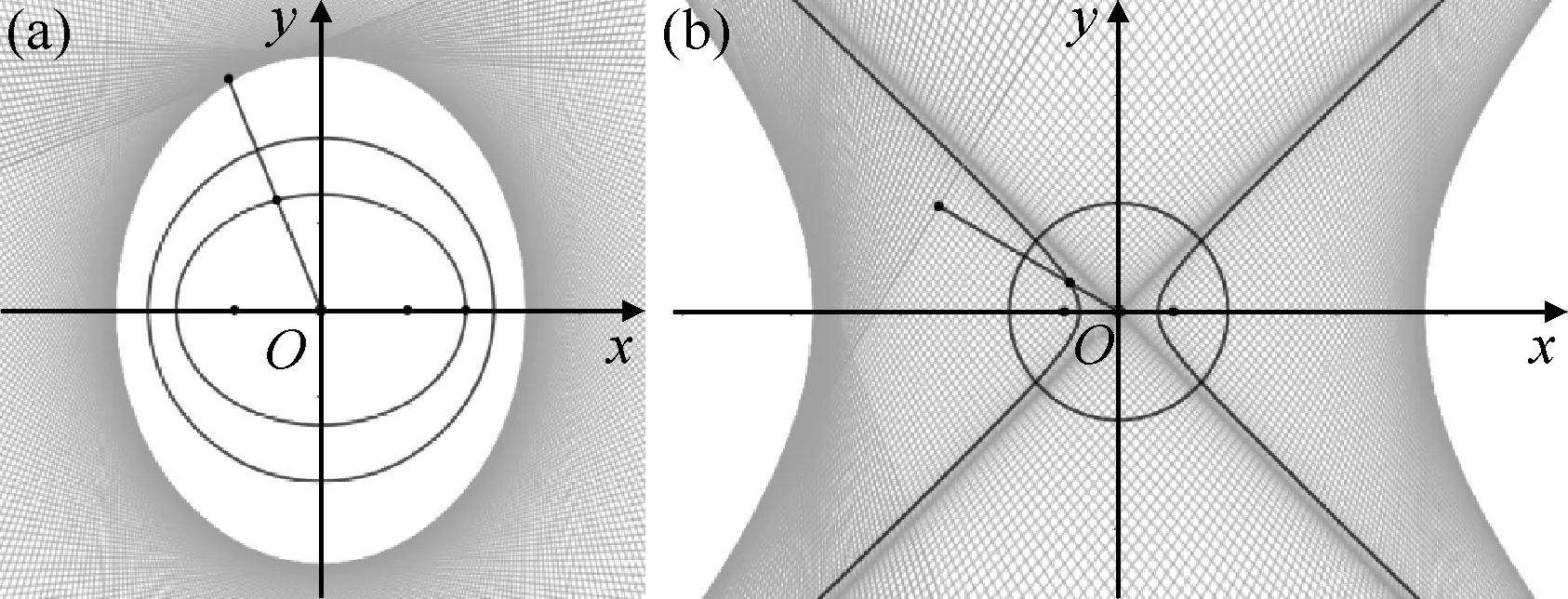
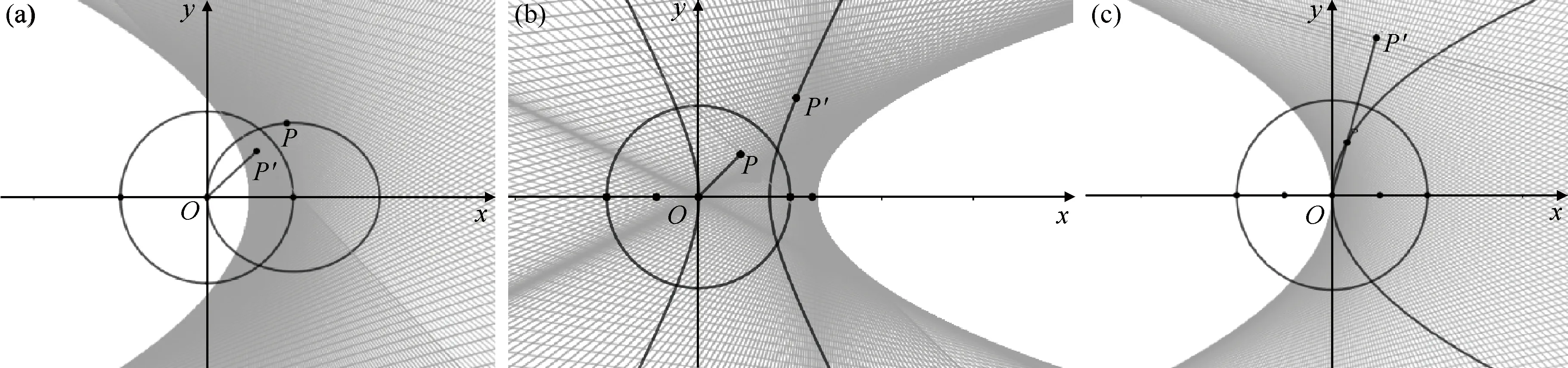
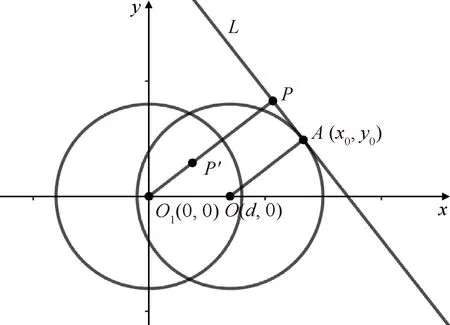
由定义可知,一个反演变换使圆C的内部变为圆C的外部.因为,若OP 若以反演基圆的圆心O为坐标原点建立平面直角坐标系,设平面上任意一点P的坐标为(x,y),其在反演基圆下的反演点P′的坐标为(x′,y′)(图2).此时,点P可用复数Z=x+yi来表示,点P′可用复数Z′=x′+y′i来表示. 图2 平面上任意一点P和反演点P′ 则由反演的定义得 |Z|·|Z′|=R2, 因此有 整理得 (1) 该式也被称为直角坐标系下反演变换的解析式. 利用反演变换的解析式,可以得到已知曲线反演后的曲线,研究曲线的反演像是曲线研究的一个有趣方法.一般来说,对于同一条曲线,选取不同的点作为反演中心,反演后得到的曲线形状也不同.但是,有的曲线在以特殊点为反演中心时,反演后得到的曲线却属于同一类型曲线.例如下述命题1. 命题1[2]若以二次曲线的一个焦点为反演中心,则二次曲线的反演像为帕斯卡蜗线[图3(a)]. 图3 不同焦点为反演中心的反演像 证明:设P(x,y)为焦点为(0,0)的二次曲线上一点(图4),设定直线为x=-p,则根据二次曲线的几何定义,有 图4 焦点为(0,0)的二次曲线上的任一点P 即 e2(x+p)2=x2+y2, 将反演变换解析式代入得 整理后得 直观地看,二次曲线可以由空间质点在某种条件下运动的轨迹来定义,即以动点来描述二次曲线.二次曲线又是其切线族的包络.而帕斯卡蜗线可以由平面内一定点M向一定圆的所有切线所作垂线的垂足轨迹来定义,若在图3中的帕斯卡蜗线上任取一点,并过该点作与其反演点连线的垂线,此处将反演点连线的垂线定义为过一点作该点与其反演点的连线,并过该点作此连线的垂线,称为过该点的反演点连线的垂线.当另一反演点在椭圆、双曲线和抛物线上运动时,此垂线簇包络会形成什么样的曲线呢?下面首先给出曲线族包络的定义: 定义2[3]设给定单参数曲线族 F(x,y,c)=0, F(x,y,c)是(x,y,c)的连续可微函数,其中c是参数.曲线族F(x,y,c)的包络是指这样的曲线:本身并不包含在曲线族F(x,y,c)中,但过这曲线的每一点,有曲线族中的一条曲线和在这点相切. 若以二次曲线的一个焦点为反演中心,P为圆锥曲线上一动点,P′为P关于给定圆C的反演点,过点P′作线段PP′的垂线.当点P在圆锥曲线上运动时,用GeoGebra画出此垂线簇包络图像(图5).由图5可知,此垂线簇包络形成的曲线为圆.若要给出严格的解析证明,需给出曲线簇包络的求法. 图5 不同焦点为反演中心时反演点连成垂线的包络图像 求法[3]由微分几何学知,曲线族F(x,y,c)的包络包含在方程组 消去c而得到的曲线族中.因此消去方程组中的参数c,求得包络满足的曲线称为F(x,y,c)的c-判别曲线.值得注意的是,在c-判别曲线中有时除去包络外,还有其他曲线.因此需要检验c-判别曲线中究竟哪一条是包络曲线. 运用曲线簇包络的求法,以反演中心为原点建立平面直角坐标系,可得出定理1. 定理1设反演基圆C的半径为R,P为圆锥曲线上一动点,P′为P关于给定圆C的反演点,过点P′作线段PP′的垂线L. (2) 因为点P(x,y)在椭圆 (3) 上,联立方程(2)~(3)消去y得 (b2v2+a2u2)x2-(2b2v2c+2a2uR2)x+ 令 F(u,v,x)=(b2v2+a2u2)x2- (4) 则 F′x(u,v,x)=(2b2v2+2a2u2)x- (5) 联立(4)式和(5)式消去x得 b4c2v4+2a2b2R2cv2u=a2b2R4v2-b6v4-a2b4v2u2, 等式两边同时除以b2v2得 b2c2v2+2a2R2cu=a2R4-b4v2-a2b2u2, 即 a2b2u2+(b2c2+b4)v2+2a2R2cu-a2R4=0, 即 a2b2u2+a2b2v2+2a2R2cu-a2R4=0, 等式两边同时除以a2b2得 以圆锥曲线中心或顶点为反演中心,反演点连线垂线包络形成的图像同样具有较强的统一性.下面以基圆圆心O为原点建立直角坐标系,用GeoGebra分别画出以圆锥曲线的中心、顶点为反演中心时反演点连线垂线的包络图像,得到定理2和3. 定理2当以焦点在x轴上的椭圆的中心为反演中心时,反演点连线垂线包络形成的图像为焦点在y轴上的椭圆[图6(a)];当以焦点在x轴上的双曲线的中心为反演中心时,反演点连线垂线包络形成的图像为焦点在x轴上的双曲线[图6(b)]. 图6 不同焦点为反演中心的反演点连线垂线的包络图像 图7 不同焦点为反演中心的反演点连线垂线包络形成的图像 在定理1中,当以圆锥曲线的一个焦点为反演中心时,反演点连线垂线包络形成的曲线都是圆.反之,2个特定位置下的圆在某种反演变换的作用下的反演图像一定是圆锥曲线.据此,下面给出如下一种轨迹法画圆锥曲线的统一方法. (1)分别以O,O1为圆心,作2个半径为R的圆,为了简化作图与证明,可使圆心O与圆心O1在一条直线上; (2)过圆O上一点A作圆O的切线L; (3)过圆心O1作一垂直于切线L的垂线段,垂足设为P; (4)作点P关于圆O1的反演点P′,当点A取遍圆O上所有点时,点P′的轨迹就是圆锥曲线. 由此可得到定理4. 定理4设圆O1和圆O的半径都为R,点A为圆O上任意一点,L为过点A的切线.作直线O1P垂直于切线L于点P,作点P关于圆O1的反演点P′.当点A取遍圆O上所有点时,点P′的轨迹为圆锥曲线.若设圆心O1与圆心O之间的距离为d,则(1)当d 图8 d不同时点P′的轨迹 图9 以圆心O为原点建立直角坐标系 直线O1P方程为 联立直线L方程与直线O1P方程,解得 因为点A(x0,y0)在圆O上,则有 (6) 将式(4)代入点P坐标得 因点P与点P′互为反演点,若设P点坐标为(x,y),P′点坐标为(x′,y′),则根据反演的定义有 即 整理后得 (7) 此时联立式(6)与(7)式得 整理后得 (R2-d2)x′2+y′2R2+2R2dx′-R4=0. (8) 最后整理得 (9) 在定理4中,若在圆O上任取一点,作该点与其关于圆O1的反演点的连线,并过该点的反演点作此连线的垂线,当该点在圆O上运动时,此垂线簇包络形成的曲线为圆锥曲线,得到定理5. 定理5设圆O1和圆O的半径都为R,点P为圆O上任意一点,点P关于圆O1的反演点为P′,过点P′且垂直于直线PP′的直线为L.当点P取遍圆O上所有点时,直线L的包络图像为圆锥曲线.若设2个圆心之间的距离为d,则 (1) 当d (2) 当d>R时,直线L的包络图像为双曲线,如图10(b); (3) 当d=R时,直线L的包络图像为抛物线,如图10(c). 图10 d不同时直线L的包络图像 (10) 因为点P(x,y)在圆 (x-d)2+y2=R2上, (11) 联立式(10)和(11)消去y得 (u2+v2)x2+(2y2d-2xR2)x0+ 令 F(u,v,x)=(u2+v2)x2+ (12) 则 Fx(u,v,x)=2(u2+v2)x+ (13) 联立式(12)和(13)消去x整理后得 (R2-d2)u2+R2v2-2dR2u-R4=0, (14) 最后整理得 (15) 则由式(14)可得,当d=R时,其轨迹为抛物线.由式(15)可得,当d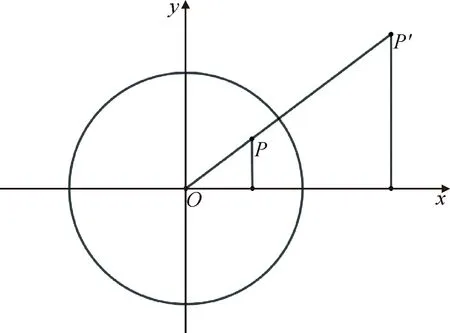
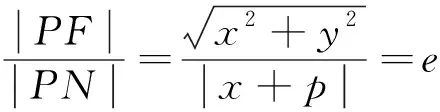
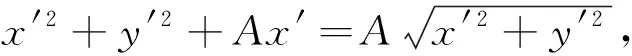
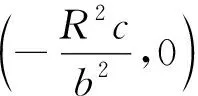
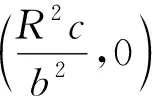
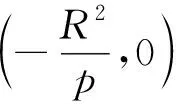
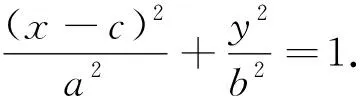
a2R4-b4v2=0,
(2b2v2c+2a2uR2)x+a2R4-b4v2,
(2b2v2c+2a2uR2).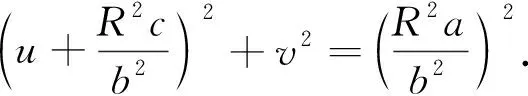
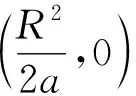
2 轨迹法画圆锥曲线的统一方法
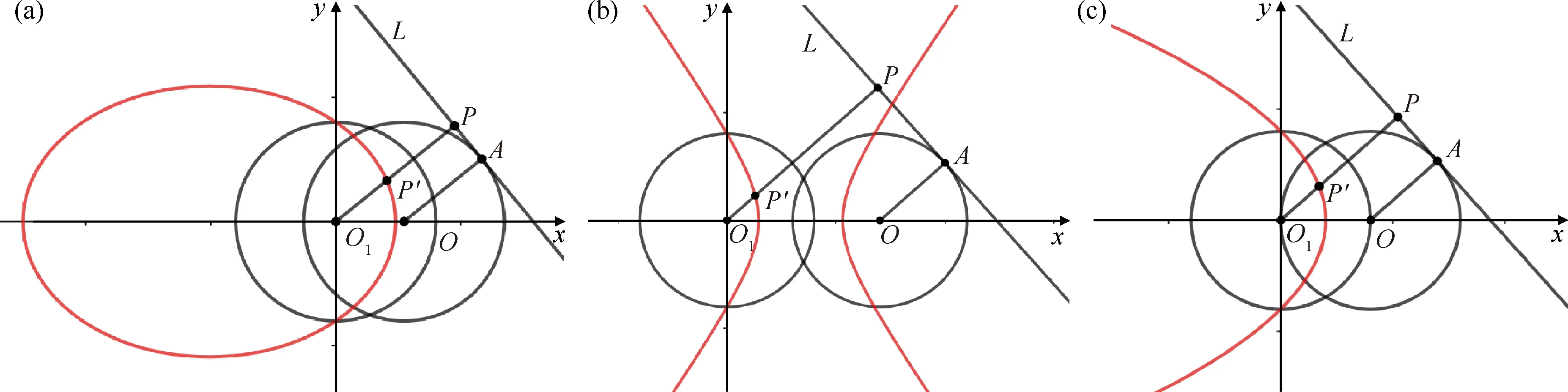
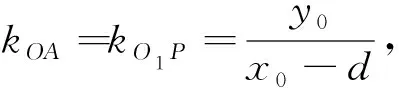
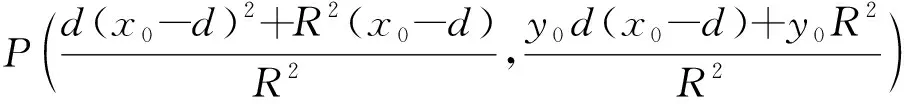
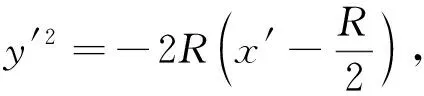
3 圆锥曲线的包络形成法
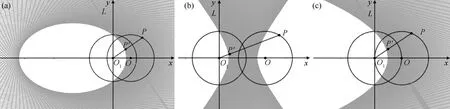
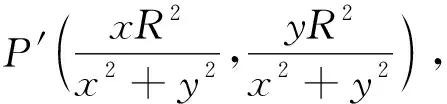
y2(d2-R2)+R4=0,
(2y2d-2xR2)x+y2(d2-R2)+R4,
(2y2d-2xR2),
