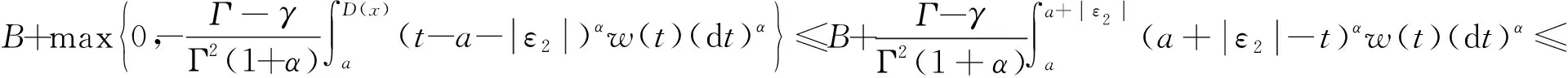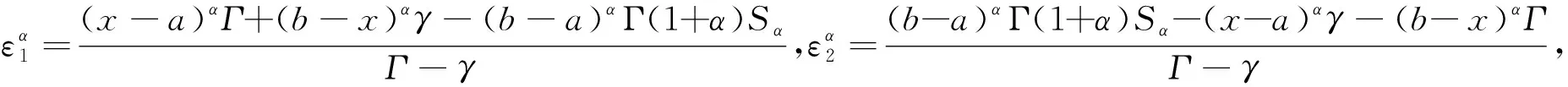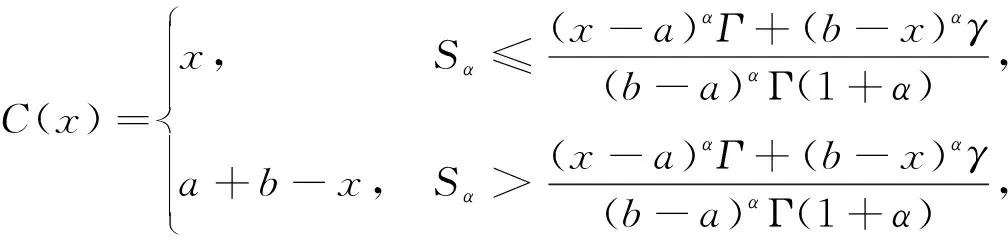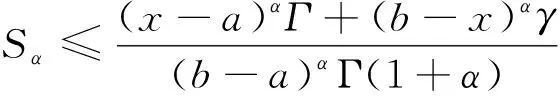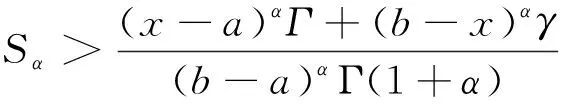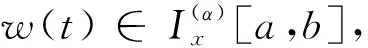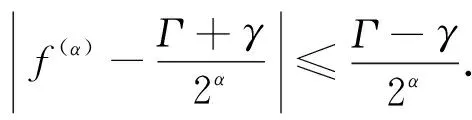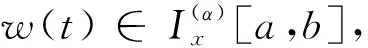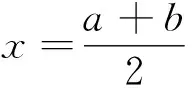分形集上的加权Ostrowski型双边不等式
2020-10-20时统业曾志红
时统业 曾志红
(1. 海军指挥学院,江苏 南京 211800; 2. 广东第二师范学院学报编辑部,广东 广州 510303)
0 引 言
设f:[a,b]→R在[a,b]上连续,在(a,b)上可微,且对任意x∈(a,b)有|f′(x)|≤M,则有
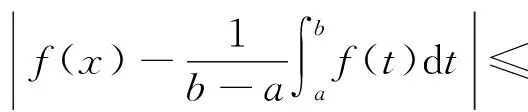
(1)
式(1)称为Ostrowski不等式[1].有关Ostrowski不等式的改进和推广见文献[2-6].
下面使用Gao-Yang-Kang的方法来描述局部分数阶导数和积分.
定义1[7]设f:R→Rα是不可微函数,如果对任意ε>0,存在δ>0,使得当|x-x0|<δ时,有|f(x)-f(x0)|<εα,则称f在点x0处局部分数阶连续.若f在区间I⊆R上局部分数阶连续,则记为f∈Cα(I).
定义2[7]设f∈Cα(a,b),则f在点x0处局部分数阶导数定义为
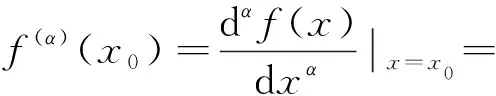
若对任意x∈I⊆R时存在f(α)(x),则记为f∈Dα(I).
定义3[7]设f∈Cα[a,b],则f在区间[a,b]上的α阶局部分数阶积分定义为
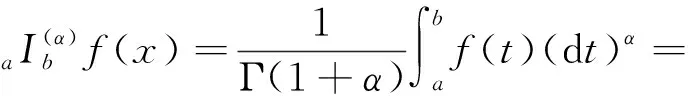
其中,a=t0 设区间I⊆R,I°是I的内部,f:I°→Rα,f∈Dα(I°),a,b∈I°,a (2) 式(2)称为广义Ostrowski不等式[8],是Ostrowski不等式在分形集的推广. (3) 式(3)称为广义加权Ostrowski不等式[9].关于广义Ostrowski型不等式还可参见文献[10-14]. (2) 局部分数阶定积分的分部积分法.设f,g∈Dα[a,b]且f(α)(x),g(α)(x)∈Cα[a,b],则 引理2[15]局部分数阶微分中值定理.设函数F(x)在[a,b]上连续,在(a,b)上α阶局部分数阶可微,则对于任意x0,x∈[a,b],x0 受参考文献[17]启发,本文用引入参数求最值的方法,建立分形集Rα上加权Ostrowski型双边不等式.为证明本文主要结果,还需要下面的引理. 定理1设f∈Dα[a,b],f(α)∈Cα[a,b],且存在常数γ,Γ∈Rα,γ<Γ,使得γ≤f(α)≤Γ,则有 (4) 其中ε1,ε2∈[x-b,x-a]满足 (5) 利用引理1(局部分数阶分部积分法)得 (6) (7) (8) 综合式(5)~(8)得 其中 于是有 (9) (10) (11) (12) 综合式(9)~(12)得 (13) (14) 利用引理1(局部分数阶分部积分法)得 (15) (16) (17) 综合式(14)~(17)得 其中 于是有 (18) (19) (20) (21) 综合式(18)~(21)有 (22) 综合式(13)和(22),则式(4)的右边2个不等式得证. 当γ≤f(α)≤Γ时,有-Γ≤(-f)(α)≤-γ.对函数-f应用已证结论,则式(4)的左边2个不等式得证. 其中ε1,ε2∈[x-b,x-a]满足 推论2设f∈Dα[a,b],f(α)∈Cα[a,b],且存在常数M∈Rα,使得|f(α)|≤M,则有 证明在推论1中取w(t)≡1α,经计算则推论2得证. 推论3设f∈Dα[a,b],f(α)∈Cα[a,b],且存在常数γ,Γ∈Rα,γ<Γ,使得γ≤f(α)≤Γ,则有 推论4设f:[a,b]→R在[a,b]上连续,在(a,b)上可微,且存在常数γ,Γ∈R,γ<Γ,使得γ≤f′≤Γ,则有 (23) 证明在推论3中取α=1,则推论4得证. 注1式(23)给出文献[2]中的Ostrowski-Grüss型不等式(8.10)的加强. 特别地,当w(t)≡1α时,有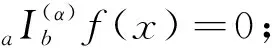
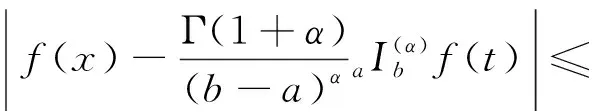
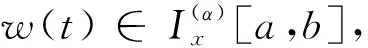
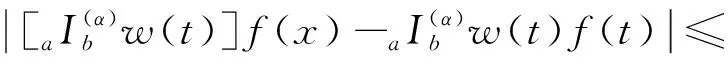
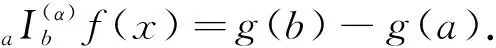
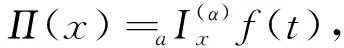
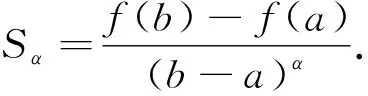
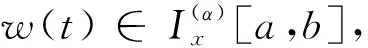
1 主要结果